再帰的なアルゴリズムの考え方に慣れるためにいくつかの有名な例を集めた。それぞれについてサンプルコードと「問題を小さくする方法」「終了条件」を記している。
注意事項：
- アルゴリズムの細かい効率よりも、論理の分かりやすさに重点を置いている
- 問題の前提に沿わない入力（例えば負の整数や小数）のチェックは省いている
- 再帰的なデータ構造や再帰を除去する方法については扱わない
- サンプルコードはRubyで書いている
基本的な再帰
階乗
nの階乗とは n! = 1*2*...*n という計算のこと。例えば「n人が一列に並ぶ方法の総数」を表せる。
「1からnまでの整数の積」と言われたらfor文などのループで書きたくなるが、再帰的な計算もできる。
factorial.rb
def factorial(n)
return 1 if n == 0
return n * factorial(n - 1)
end
p factorial(5) #=> 120
- 問題を小さくする方法
- ひとつ小さい値(n-1)での計算結果に n を掛ける
- 終了条件
- nが0なら値は1。そう定めておくのが色々な状況で自然
- 備考
- 急激に大きくなるので、任意長整数を扱えない環境では倍精度実数を返しておくといい（ n=22 までは正確に求まり、その後は近似値になる）
最大公約数（GCD）
与えられた2つの数を共に割り切れる最大の数を求めたいことがある。算数では分数の約分に使えるし、応用では長方形の画像を正方形のタイルに分割することなどもできる。
実際の求め方だが、公約数を見つけて割っていく方法や素因数分解する方法は計算が大変（学校のテストならともかく）。ユークリッドの互除法を使うと効率よく求められる。
gcd.rb
def gcd(a, b)
return a.abs if b == 0
return gcd(b, a % b)
end
p gcd(1920, 1080) #=> 120
以下の説明では簡単のために a, b が0以上の整数であるとする。負の整数へ対応するにはサンプルコードの通り絶対値を返せばいい。
- 問題を小さくする方法
- aとbの最大公約数は、bとa%b（aをbで割った余り）の最大公約数と等しい。b > a%b なので第2引数は必ず元より小さくなる
- 終了条件
- bがゼロのとき、aが最大公約数。ちょうどa%bがゼロ除算で計算できない
- 備考
- 数学的な説明のときは a ≧ b という前提をおくことがあるが、実装の際は考慮不要。a < b なら再帰呼び出しによって
gcd(a, b)→gcd(b, a)→...と自動で入れ替わる - 再帰は十進の桁数の5倍以下で済むので、64bit整数（20桁）程度ならスタックオーバーフローはまず起きない
- 関数の最後の処理が再帰呼び出しである末尾再帰は、再帰を簡単に除去できる。コンパイラが自動で除去してくれる可能性がある
- 数学的な説明のときは a ≧ b という前提をおくことがあるが、実装の際は考慮不要。a < b なら再帰呼び出しによって
累乗
aのn乗 a^n = a*a*...*a を求める演算。一見aをn回掛けるだけでありループで十分そうだが、nが非常に大きい場合は時間がかかってしまう。バイナリ法を使えばnの桁数に比例した回数まで掛け算を減らせる。
power.rb
def power(a, n)
return 1 if n == 0
b = power(a, n / 2); b *= b # b <- (a^(n/2))^2
# b = power(a * a, n / 2) # b <- (a^2)^(n/2)
b *= a if n % 2 == 1
return b
end
if $0 == __FILE__
p power(2, 30) #=> 1073741824
p power(3, 19) #=> 1162261467
# Fermat's little theorem
a = 3 # any integer
n = 6700417 # prime number
p power(a, n) % n #=> a % n
end
3^6700417 は約320万桁の数（出力すると3.2MB）なので、対話型の実行環境などで試すときは累乗自体の結果を表示させないよう要注意。
- 問題を小さくする方法
- a^n = a^(n/2*2) = (a^(n/2))^2 または (a^2)^(n/2) と式変形すると指数を半分にできる
- 2乗するタイミングは累乗の外側と内側のどちらでも可能（サンプルコード4,5行目）
- 2乗の計算については累乗ではなく単に同じ数を掛ける
- nが奇数であれば
n/2は端数を切り捨てるので、追加でaを掛ける（a^n = (a^(n-1))*a）
- a^n = a^(n/2*2) = (a^(n/2))^2 または (a^2)^(n/2) と式変形すると指数を半分にできる
- 終了条件
- 0乗であれば1を返す1。指数を半分にしようとすると、0のまま変わらないので無限ループに陥る
- 備考
- 剰余をとりながらの累乗や、行列の累乗などにもすぐ応用できる
- 掛け算の回数を「最小」にするのは、バイナリ法では達成できず、非常に難しい問題となっている（→addition-chain exponentiation）
ハノイの塔
有名なパズル。3本の棒のひとつにささってピラミッド状に積まれているn枚の円盤を、大きさを逆転させないように1枚ずつ移動させて、全て別の1本の棒に積み直す手順を考える。重ねて収納する鍋と3ヶ所の収納スペースで試してもいい。
hanoi.rb
RODS = ["A", "B", "C"]
def hanoi(n, from, to)
return if n == 0 # do nothing
temp, = RODS - [from, to]
hanoi(n - 1, from, temp)
puts "move disk##{n} from #{from} to #{to}"
hanoi(n - 1, temp, to)
return
end
hanoi(4, RODS.first, RODS.last)
output
move disk#1 from A to B
move disk#2 from A to C
move disk#1 from B to C
move disk#3 from A to B
move disk#1 from C to A
move disk#2 from C to B
move disk#1 from A to B
move disk#4 from A to C
move disk#1 from B to C
move disk#2 from B to A
move disk#1 from C to A
move disk#3 from B to C
move disk#1 from A to B
move disk#2 from A to C
move disk#1 from B to C
- 問題を小さくする方法
- 円盤の山を「上n-1枚の塊」と「下1枚」とみて考える
- 上側を仮置き場に退避させてから下側を目的地へ移動させ、上側を仮置き場から目的地に移動させる
- 終了条件
- 円盤が0枚なら何もしない。円盤の無いパズルというのは奇妙だが、認めれば短く実装できる
- それが嫌なら、円盤が1枚ならただ
fromからtoへ動かすだけ、と実装してもいい
- 備考
-
tempは関数の中で求めずに引数として外から渡すよう改善できる
-
hanoi_2.rb
def hanoi(n, from, to, temp)
return if n == 0 # do nothing
hanoi(n - 1, from, temp, to)
puts "move disk##{n} from #{from} to #{to}"
hanoi(n - 1, temp, to, from)
return
end
hanoi(4, "A", "C", "B")
分割統治法
大きな問題を小さな問題に分割してそれぞれ解き、結果をまとめて元の問題の解を得る手法。解法が分からないときの手掛かりになるだけでなく、計算時間が問題サイズに従って急激に伸びる場合には直接全体を解くより高速になることが多々ある。
分割してできた小さな問題をどう解くかは自由で、同じアルゴリズムを適用して再帰的に解いていくのが一番分かりやすい。分割できないところまで小さくするのがアルゴリズムとして綺麗だが、適度に小さくなった段階で別のアルゴリズムに切り替えたほうが高速だったりする。
クイックソート
一般的な用途では最も速いソート方法。
quick_sort.rb
def quick_sort(ary)
ary = ary.dup # preserve the input array
n = ary.size
return ary if n <= 1
pivot = ary.delete_at(rand(n))
ary_less_eq, ary_greater = ary.partition { |x| x <= pivot }
return quick_sort(ary_less_eq) + [pivot] + quick_sort(ary_greater)
end
if $0 == __FILE__
ary = Array.new(10) { rand(10) }
puts "input: #{ary}"
puts "output: #{quick_sort(ary)}"
end
- 問題を小さくする方法
- 適当な値（ピボット）を選び、それより小さいものと大きいものに分けた配列を作る。ピボットを抜いておけば、分けた配列の要素数は必ず元より小さくなる
- 分けた配列それぞれをソートして結合するとソート完了
- 終了条件
- 備考
- 元の配列内で前後に要素を寄せれば、新しい配列を作らずに分割できて結合の手間もなくなる。それを再帰的に繰り返せば内部ソートとなる
- 分割した配列が同じ大きさになると高速だが、片寄り続けるとバブルソート並みに遅くなる
- 単純な実装では、ソート済みの配列や全て同じ値の配列に弱いことがある
- 最悪に近いケースでは再帰呼び出しも増え、スタックオーバーフローの危険がある（例：
quick_sort([1] * 10**4)）
マージソート
分割統治法を使った別のソート方法。クイックソートは分割時の処理でソートするのに対し、マージソートは併合時の処理でソートする。ソートの性質も両者で色々と異なる。
merge_sort.rb
def merge_sort(ary)
n = ary.size
return ary.dup if n <= 1
ary_left = merge_sort(ary[0...(n/2)])
ary_right = merge_sort(ary[(n/2)..-1])
ary = []
loop do
if ary_left.empty?
ary.concat(ary_right)
break
elsif ary_right.empty?
ary.concat(ary_left)
break
elsif ary_left[0] <= ary_right[0] # stable
ary << ary_left.shift
else
ary << ary_right.shift
end
end
return ary
end
if $0 == __FILE__
ary = Array.new(10) { rand(10) }
puts "input: #{ary}"
puts "output: #{merge_sort(ary)}"
end
- 問題を小さくする方法
- 配列を2分割し、それぞれソートしておく
- 2つの配列を比較しながら小さい順に要素を抜き出していき、ソートされた1つの配列を作る
- 終了条件
- 要素数が0か1なら、配列をそのまま返す2。分割しようとすると無限ループに陥る
- 備考
- 均等に分割できるので最悪ケースでも高速に動作する
- 自然と安定ソートを実装できる
高速フーリエ変換（FFT）
離散フーリエ変換（DFT）を高速に計算するアルゴリズム。データの「波」を扱う様々な処理を実用化する基礎になっている。
一口にFFTと言っても状況に応じて種類があるが、ここでは最もよく使われるCooley-Tukey3型FFTを扱う。原理は難しいので説明を省く代わりに、速度差を実感できるようサンプルコードにベンチマークを付属している。
参考：
- FFT (高速フーリエ・コサイン・サイン変換) の概略と設計法: 1.2.3. 混合基数アルゴリズム
- Cooley–Tukey FFT algorithm: 3. General factorizations
fft.rb
require 'prime'
def twiddle_factor(n, m)
return Complex.polar(1, -2 * Math::PI * m / n)
end
def dft(ary)
n = ary.size
w = Array.new(n) { |m| twiddle_factor(n, m) }
result = Array.new(n) do |k|
a = Array.new(n) do |j|
ary[j] * w[j * k % n]
end
a.inject(:+)
end
return result
end
def fft(ary)
n = ary.size
return ary.dup if n <= 1
n1 = Prime.instance.find { |p| n % p == 0 }
n2 = n / n1
return dft(ary) if n == n1
w = Array.new(n) { |m| twiddle_factor(n, m) }
ary_2d = ary.each_slice(n2).to_a
ary_2d = ary_2d.transpose.collect! do |ary1|
fft(ary1) # length: n1
end.transpose
ary_2d = ary_2d.collect!.with_index do |ary2,j1|
# 0 <= j1 < n1, 0 <= k2 < n2
ary2.collect!.with_index { |a,k2| a * w[j1 * k2] }
end
ary_2d = ary_2d.collect! do |ary2|
fft(ary2) # length: n2
end
result = ary_2d.transpose.flatten!
return result
end
if $0 == __FILE__
require 'benchmark'
# test data: sin(kx)
n = 2**3 * 3**2 * 5**2 #=> 1800
k = 7
ary = Array.new(n) { |j| Math.sin(2 * Math::PI * j * k / n) }
puts "test data: sin(#{k}x)"
puts "samples: #{n}"
puts
# benchmark
result_dft = result_fft = nil
Benchmark.bm(5) do |rep|
rep.report('DFT:') { result_dft = dft(ary) } # slow
rep.report('FFT:') { result_fft = fft(ary) } # fast
end
puts
# error
def calc_error(n, k, result)
return 0 if n == 0
diff = result.dup
diff[k] -= -n / 2.0 * Complex::I
diff[n-k] -= n / 2.0 * Complex::I
return Math.sqrt(diff.map(&:abs2).inject(:+))
end
puts "exact solution: c[#{k}] = #{-n/2.0}i, c[#{-k}] = #{n/2.0}i"
puts "DFT error: #{calc_error(n, k, result_dft)}"
puts "FFT error: #{calc_error(n, k, result_fft)}"
end
output
test data: sin(7x)
samples: 1800
user system total real
DFT: 5.030000 0.040000 5.070000 ( 5.374379)
FFT: 0.120000 0.000000 0.120000 ( 0.116416)
exact solution: c[7] = -900.0i, c[-7] = 900.0i
DFT error: 3.2666337306581952e-12
FFT error: 3.3549317193241563e-12
N=1800 のときで40倍以上の速度差が出た。もっと大きな問題だとこの倍率はますます大きくなり、 dft で計算が終わらない場合でも fft ではすぐ完了する。浮動小数点演算のため計算方法を変えると結果も少し変わるものの、厳密解からの誤差はほぼゼロのままなので問題ないだろう。
- 問題を小さくする方法
- 長さ N=N1N2 のDFTは、長さ N1 のDFTを N2 回、長さ N2 のDFTを N1 回計算することで求められる。途中で回転因子 W を掛ける必要がある
- 終了条件
- Nが0か1なら変換後も同じ値2。素因数を探す際に不都合なので最初に弾く
- Nが素数なら他のDFTアルゴリズムで計算する。分割しようとすると無限ループに陥る
-
n1は必ず素数なので、if文にせずループ内でdft(ary1)と直接呼び出してもいい
-
- 備考
- Nが2の累乗のときは、細かく分割できるだけでなくほとんどの回転因子が±1で計算を簡略化でき、適切に実装すれば非常に高速となる
fft のメイン計算部分では、配列を一時的に2次元化して縦横にDFTを計算したりセル毎に回転因子を掛けたりしている。2次元配列の走査方向が入出力時で異なることに注意。
メモ化再帰
メモ化という手法を再帰計算に適用する。考え方は簡単で、「以前に計算結果をメモしたので答えを知っている」ということを再帰の終了条件に追加する。これによって、同じ部分問題を何度も解く羽目になるタイプの再帰アルゴリズムを高速化できる。特に最適化問題を再帰で解くときによく現れ、動的計画法の実現方法のひとつとなっている。
- あくまで高速化のためであってメモ化しなくても動くため、終了条件のところで一々説明はしない。
- メモ化しただけではスタックオーバーフローは防げないことに注意。あらかじめ小さい問題を解いてメモを埋めることで初めて対処できるようになる。
- 以下の例では、「メモが無ければ計算・保存したうえでメモの値を返す」という処理には
||=を利用している。これが利用できない状況では、ダミーの値などでメモの有無を判別して処理を分ければいい。
フィボナッチ数列
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... と、前2つの数を足すことで求まる数列。単純ながら色々なところで登場するので興味深い。（例えば、隣り合う数はユークリッドの互除法の最悪ケースとなる）
定義自体が再帰的なので再帰関数を実装するのは簡単。しかしそのままでは計算に時間がかかるので、メモ化を施す必要がある。
fibonacci.rb
$table = []
def fibonacci(n)
return $table[n] ||= (
case n
when 0 then 0
when 1 then 1
else fibonacci(n - 2) + fibonacci(n - 1)
end
)
end
p fibonacci(30) #=> 832040
p fibonacci(35) #=> 9227465
- 問題を小さくする方法
- 前項2つを求めて足す
- 終了条件
- nが0と1のときの値は決められている
- 備考
- メモ化しない場合、関数呼び出しは
fibonacci(n)に比例した回数だけ発生する- n=30 なら2692537回、 n=35 なら29860703回
-
$table[n] ||=を削除すればメモ化しなくなり、nが増えると一気に遅くなることが確かめられる
- テーブル初期化時に終了条件を組み込むと、以下のように終了条件の分岐を省略できる
- メモ化しない場合、関数呼び出しは
fibonacci2.rb
$table = [0, 1]
def fibonacci(n)
return $table[n] ||= fibonacci(n - 2) + fibonacci(n - 1)
end
p fibonacci(30) #=> 832040
p fibonacci(35) #=> 9227465
レーベンシュタイン距離
ある文字列から別の文字列へ編集するには最小で何文字だけ挿入・削除・置換すればいいかを数える。文字列がどれくらい似ているかを測る方法のひとつ。
levenshtein_distance.rb
class LevenshteinDistance
def calc(str1, str2)
@str1 = str1
@str2 = str2
n1 = @str1.length
n2 = @str2.length
@table = Array.new(n1 + 1) { Array.new(n2 + 1) }
return __calc__(n1, n2)
end
private
# distance between @str1[0...n1] and @str2[0...n2]
def __calc__(n1, n2)
return @table[n1][n2] ||= (
if n1 == 0
1 * n2 # insert all characters
elsif n2 == 0
1 * n1 # delete all characters
else
ins = __calc__(n1 , n2 - 1) + 1
del = __calc__(n1 - 1, n2 ) + 1
sub = __calc__(n1 - 1, n2 - 1) + sub_score(n1, n2)
[ins, del, sub].min
end
)
end
def sub_score(n1, n2)
return @str1[n1-1] == @str2[n2-1] ? 0 : 1
end
end
if $0 == __FILE__
p LevenshteinDistance.new.calc("Tuesday", "Thursday") #=> 2
end
- 問題を小さくする方法
- より短い部分文字列の距離については分かっていると仮定する
- 末尾の文字を挿入・削除・置換したと仮定してスコアを計算し、最良のものを採用する
- 終了条件
- 片方の文字列が空なら、もう片方の文字列の長さがスコア（全追加or全削除ということ）
- 備考
- 文字列間の距離だけでなく実際の編集方法を知りたいときは、完成した表をゴールからスタートへ向かって低スコア部分をたどればいい
dump_table
| T h u r s d a y
---+------------------------------------
| *0 1 2 3 4 5 6 7 8
T | 1 *0 *1 2 3 4 5 6 7
u | 2 1 1 *1 2 3 4 5 6
e | 3 2 2 2 *2 3 4 5 6
s | 4 3 3 3 3 *2 3 4 5
d | 5 4 4 4 4 3 *2 3 4
a | 6 5 5 5 5 4 3 *2 3
y | 7 6 6 6 6 5 4 3 *2
ナップサック問題
重さと価値の分かっている品物のリストが与えられたときに、あるナップサックに詰める品物を決められた重さ以内で価値最大となるよう選ぶ問題。日常生活でも使える場面が多そうな最適化問題。
問題のバリエーションのひとつに同じ品物を複数選べるかがあり、サンプルコードは各品物を1個までしか選べない「0-1 ナップサック問題」について解いている。
knapsack.rb
Item = Struct.new(:weight, :value, :info)
class Knapsack
def calc(items, weight_limit)
init_tables(items, weight_limit)
return __calc__(items.size, weight_limit)
end
private
def init_tables(items, weight_limit)
n = items.size
@items = [nil] + items # one-based indexing
@table = Array.new(n + 1) { Array.new(weight_limit + 1) }
return
end
# memoized function
def __calc__(n, weight_limit)
return @table[n][weight_limit] ||= __calc_org__(n, weight_limit)
end
# original function (renamed from "__calc__")
def __calc_org__(n, weight_limit)
return 0 if n == 0
item = @items[n]
bound = [weight_limit / item.weight, 1].min # 0 or 1
values = (0..bound).collect do |k|
__calc__(n - 1, weight_limit - item.weight * k) + item.value * k
end
return values.max
end
end
if $0 == __FILE__
items = [
# weight [g], value [yen], name
Item.new(90, 108, "cookie"),
Item.new(60, 74, "potato chips"),
Item.new(85, 138, "gummi"),
Item.new(50, 95, "chocolate"),
Item.new(58, 70, "youkan"),
]
weight_limit = 200
p Knapsack.new.calc(items, weight_limit) #=> 307
end
再帰関数が多少長いため、再帰アルゴリズムとメモ化処理とを別の関数に分けた。このようにメモ化は機械的に後付けでき、言語によっては自動化できることもある。
- 問題を小さくする方法
- 品物リストがひとつ少ない場合については、任意の重さ制限に対する最大価値が全て分かっていると仮定する
- 新しい品物
@items[n]を入れる場合と入れない場合の価値を計算し、大きいほうを選ぶ- 入れる場合というのは、重さ制限から新しい品物分を抜いたときの最大価値＋新しい品物の価値、と計算できる
- ただし新しい品物を入れる余裕がないときは、入れない場合の一択になる
- 終了条件
- 品物リストが空なら、何も詰められないので合計価値は0
- 備考
- 品物が少なくて重さ制限がゆるい場合は、メモ済みの状態に当たる可能性が低いので、全探索で計算したほうが効率いいことがある
ところで、プログラミング問題としては最大値だけ答えることが多いが、最大にするために実際に何を選べばいいのかを知りたいこともある。再帰関数の中で最大値を選ぶ際にその品物の選び方（k）も一緒に記録するのが直接的だが、上で定義した Knapsack#__calc__ により各状態の最適解を出せるので、それをもとに選び方を後から検証していくこともできる。
knapsack_util.rb
require './knapsack.rb'
class Knapsack
def select_items(items, weight_limit)
init_tables(items, weight_limit)
return __select_items__(items.size, weight_limit)
end
private
def __select_items__(n, weight_limit)
return [] if n == 0
item = @items[n]
bound = [weight_limit / item.weight, 1].min # 0 or 1
value_max = __calc__(n, weight_limit)
num = (0..bound).find do |k|
__calc__(n - 1, weight_limit - item.weight * k) + item.value * k == value_max
end
return __select_items__(n - 1, weight_limit - item.weight * num) << [item, num]
end
end
if $0 == __FILE__
items = [
# weight [g], value [yen], name
Item.new(90, 108, "cookie"),
Item.new(60, 74, "potato chips"),
Item.new(85, 138, "gummi"),
Item.new(50, 95, "chocolate"),
Item.new(58, 70, "youkan"),
]
weight_limit = 200
selected_items = Knapsack.new.select_items(items, weight_limit)
weight = value_max = 0
selected_items.each do |item,num|
weight += item.weight * num
value_max += item.value * num
end
puts "weight : #{weight} (<= #{weight_limit})"
puts "value_max : #{value_max}"
puts "selected_items : "
selected_items.each do |item,num|
puts " #{num} * #{item}"
end
end
output
weight : 195 (<= 200)
value_max : 307
selected_items :
0 * #<struct Item weight=90, value=108, info="cookie">
1 * #<struct Item weight=60, value=74, info="potato chips">
1 * #<struct Item weight=85, value=138, info="gummi">
1 * #<struct Item weight=50, value=95, info="chocolate">
0 * #<struct Item weight=58, value=70, info="youkan">
相互再帰
これまでの再帰関数は自分自身を呼び出していたが、複数の関数がお互いを呼び出してもいい。問題が小さくなっているのか自明でないこともあり、正しい論理を組み立てられず処理が終わらなくなる危険が大きい。
偶奇判定
実用性は無いが簡単な例。（参考）
even_odd.rb
def even?(n)
return n == 0 ? true : odd?(n - 1)
end
def odd?(n)
return n == 0 ? false : even?(n - 1)
end
p even?(4) #=> true
p even?(7) #=> false
- 問題を小さくする方法
- ひとつ小さい値の偶奇は逆
- 終了条件
- 0は偶数
再帰下降構文解析
文字列の構造を読み取る方法のひとつで、相互再帰になっている構文定義の各規則をそのまま関数にする。構文解析器（パーサ）のコードを書くのは手作業でも比較的簡単で、さらに構文定義から自動生成するコード（パーサジェネレータ）も実装しやすい。
ここでは「1桁の整数・加算・乗算・括弧のみの数式を解釈して計算結果を返す」構文解析器を作ってみる。構文はParsing Expression Grammar（PEG）に基づいて定義する。
参考：
-
The Packrat Parsing and Parsing Expression Grammars Page
- Parsing Expression Grammars: A Recognition-Based Syntactic Foundation
- PEG.js
parsing_expression_grammar
additive <- multitive ('+' multitive)*
multitive <- primary ('*' primary )*
primary <- decimal / '(' additive ')'
decimal <- [0-9]
expr_parser.rb
class ExprParser
def parse(str)
@str = str
index, value = additive(0)
return index == @str.length ? value : nil
end
private
FAILED_RESULT = [nil, nil].freeze
private_constant :FAILED_RESULT
def additive(idx)
idx, val = multitive(idx)
return FAILED_RESULT unless val
loop do
break if @str[idx] != '+'
i, v = multitive(idx + 1)
break unless v
idx = i
val += v
end
return [idx, val]
end
def multitive(idx)
idx, val = primary(idx)
return FAILED_RESULT unless val
loop do
break if @str[idx] != '*'
i, v = primary(idx + 1)
break unless v
idx = i
val *= v
end
return [idx, val]
end
def primary(idx)
i, v = decimal(idx)
return [i, v] if v
return FAILED_RESULT if @str[idx] != '('
idx, val = additive(idx + 1)
return FAILED_RESULT unless val
return FAILED_RESULT if @str[idx] != ')'
return [idx + 1, val]
end
def decimal(idx)
match_data = /\G[0-9]/.match(@str, idx)
return FAILED_RESULT unless match_data
match_str = match_data[0]
return [idx + match_str.length, match_str.to_i]
end
end
if $0 == __FILE__
p ExprParser.new.parse("1+2*(3*(4+5)+6)*(7+8)+9") #=> 1000
p ExprParser.new.parse("1+2*(3*(4+5)+6*78)+9") #=> nil
end
自己再帰では「問題を小さくする」「再帰呼び出しせず終了する」役割を自分自身で持たなければいけなかったが、相互再帰ではそれらが全体のどこかにあればいい。なので構造が非常に分かりにくい上に、それらの役割が必ず呼ばれることも保証しづらい。
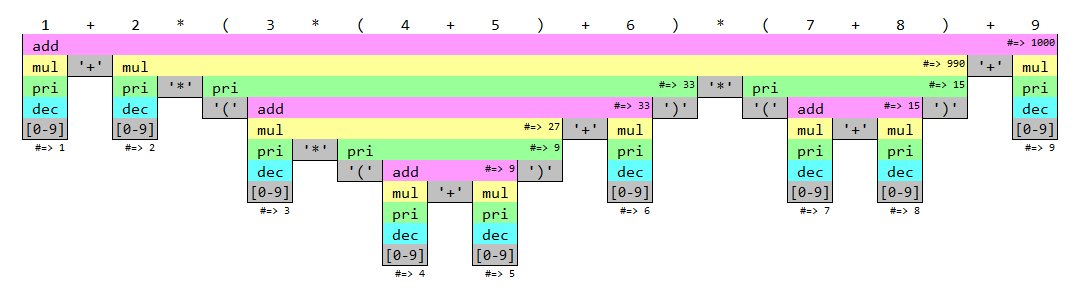
再帰下降構文解析のコードは複雑に感じるが、実際の動きを図にすると相互再帰の仕組みが分かりやすい。今回の例にした数式1では、関数は以下の図のように呼び出されて4構文解析が成功する。左上から始まり壁に沿って、関数呼び出しで下に潜り、底に着いたら文字の読み取りで右に進み、上に戻るときに関数が結果を返す。そして完了後、例えば4ヶ所の additive に注目すると、直下は必ず multitive … '+' multitive というパターンになっていることが確認できる。
- 問題を小さくする方法
- それぞれの構文規則は、文字列や他の規則を組み合わせた再帰的な表現から成る。各表現は規則全体と同じかより短い文字列にマッチする
- 以下のパターンは無限ループになるのでダメ
- 規則の先頭で同じ規則を参照する（左再帰）。直接でなくても相互再帰の結果としてなることがある
- 空文字列にマッチする表現を
*などで無限に繰り返す
- 終了条件
- 「再帰呼び出しをせず」という意味では、文字列を読み取ることが終了条件にあたる。読み取り専用の規則に切り出しておくと分かりやすい
- 再帰関数の実装方法
- 構文規則に対応する関数を用意する。まずは入出力の仕様だけ決めておく（以下は一例）
- 引数は文字列の読み取り位置
- 解析成功なら、読み進めた位置と解析結果を返す
- 解析失敗なら、失敗を表す何かを返す
- 関数の副作用（インスタンス変数の書き換えなど）は無し
- 構文解析するように関数を実装する
- 読み取り位置を常に管理する。失敗時の差し戻し地点も必要なので、値の上書きには要注意
- 現在位置で期待する規則の関数を呼び出し、解析結果を受け取る。文字列を期待するなら直接調べてもいい
- 受け取った結果をもとに、読み進めた先で解析を続けたり、失敗前の位置から別の解析を試したりする
- 規則の終わりまでいったら解析成功、途中で詰まったら解析失敗
- 構文規則に対応する関数を用意する。まずは入出力の仕様だけ決めておく（以下は一例）
- 備考
- 正しい数式の後に余計な文字列が続かないことは
ExprParser#parseの最後で確認している- これをしないと、例に出した数式2は
"1+2"として構文解析成功してしまう - PEGは「先読み」の文法があり、終端の確認を構文定義に含めることもできる
- これをしないと、例に出した数式2は
- 例では同じ関数に同じ位置を与えると常に同じ結果を返す。よってもっと複雑な構文になればメモ化することで高速化が図れる（パックラット構文解析）
- 正しい数式の後に余計な文字列が続かないことは
おまけ
再帰呼び出しの限界
再帰呼び出しはいくらでも深く実行できるわけではなく、どこかでスタックオーバーフローを起こす。その限界を簡単なコードで測ってみる。
recurse_limit.rb
def recurse_limit(count = 1)
return recurse_limit(count + 1)
rescue SystemStackError
return count
end
begin
p recurse_limit
rescue SystemStackError
p 0
end
- 問題を小さくする方法
- 関数呼び出しでスタックを消費する
- 終了条件
- 呼び出しできず、何かしらのエラーが発生する
- 備考
- 引数が多いなどでスタックをより消費していると呼び出せる回数が減る
まとめ
見てきた再帰アルゴリズムの考え方を集約する。他の再帰であっても同様の考え方をすればいい。
- 問題を小さくする方法：無限ループに陥らないために必須
- より小さい問題については解けると仮定して、その結果から元の解を得る
- 問題の大きさを n から n-1 に減らすパターンが最も単純
- n/2 のようなパターンでは、問題が小さくならない状況（n=0）を見逃さないように
- 問題を2つ以上の小さい問題に分割することもある
- 複数の問題を行き来してもいい。問題が小さくなっているか分かりにくいので注意がいる
- より小さい問題については解けると仮定して、その結果から元の解を得る
- 終了条件
- 問題をこれ以上小さくできない場合については必須
- 大きさが0や1などのときが基本的。解が自明なことが多い
- 再帰処理がエラーを起こすような場合は気づきやすい
- まだ再帰できるときに終了しても構わない
- 再帰でやり切るよりも、ある程度まで小さくなった段階でアルゴリズムを変えたほうが効率いいことがある
- 「すでに同じ計算をしていて答えを知っている」でも終了できる
- 問題をこれ以上小さくできない場合については必須
-
a=0 のとき（0の0乗）が悩ましいが、指数が整数のゼロなら同様に結果を1とすることが多い ↩
-
例では n ≧ 2 の場合と一貫性を持たせるために、常に新しい配列を作って返している ↩
-
たまに見かけるがTu"r"keyではない https://ja.wikipedia.org/wiki/ジョン・テューキー ↩
-
解析失敗して引き返す（バックトラック）ぶんの試行は表示していない。例えば、実際は
primaryは'('を読み取る前に必ずdecimalを呼び出して失敗している。 ↩