競技プログラミングで解説を読んで next_permutation アルゴリズムの存在を知ったので1、どう求めるのか勉強してRubyでメソッドを実装してみることにした。
辞書順の順列
「順列」は、与えられた要素を並べて作れる列。Rubyなら Array#permutation で全て列挙できる。汎用的には要素 n 個のうち k 個を選んで並べることを考えるが、今回は n = k 、つまり与えられた全要素を並べ替えること(置換)だけ考える。
辞書順というのは、簡単に言ってしまえばこの列挙した順列をソートしたもの2。例えば ["a", "b", "c"] の順列をソートすれば以下のようになる。
1: ["a", "b", "c"]
2: ["a", "c", "b"]
3: ["b", "a", "c"]
4: ["b", "c", "a"]
5: ["c", "a", "b"]
6: ["c", "b", "a"]
それぞれの順列に順序をつけたことで、「ある順列の次の順列は?」という問いが可能になる。もちろん一旦全ての順列を列挙してから探すこともできるが、列挙せずに求められるならそのほうが効率いい。
ちなみに辞書順で先頭に来る順列は、要素を昇順にソートしたものである。また最後に来る列は、要素を降順にソートしたものである。
ところで、ふつうの順列は互いに区別できる要素を並べることを考えている。与えられた要素に同じものがあると、単純な列挙では同じ順列が複数できてしまう。例えば ["a", "a", "b"] の順列をソートすれば以下のようになる。
1: ["a", "a", "b"]
2: ["a", "a", "b"]
3: ["a", "b", "a"]
4: ["a", "b", "a"]
5: ["b", "a", "a"]
6: ["b", "a", "a"]
列挙した場合は重複を #uniq で省いたりしておく必要がある。 next_permutation の場合は重複を回避して次の順列を導ける(ということが解説に書いてあって驚いた)。
求め方
もっと長い順列で試していると、先頭の方はあまり変化しないことに気付く。どの位置までが変化するのか分かれば楽になる。
[1, 1, 1, 2, 2, 3].permutation.sort.uniq (60通り)
[1, 1, 1, 2, 2, 3]
[1, 1, 1, 2, 3, 2]
[1, 1, 1, 3, 2, 2]
[1, 1, 2, 1, 2, 3]
[1, 1, 2, 1, 3, 2]
[1, 1, 2, 2, 1, 3]
[1, 1, 2, 2, 3, 1]
[1, 1, 2, 3, 1, 2]
[1, 1, 2, 3, 2, 1]
[1, 1, 3, 1, 2, 2]
[1, 1, 3, 2, 1, 2]
[1, 1, 3, 2, 2, 1]
[1, 2, 1, 1, 2, 3]
[1, 2, 1, 1, 3, 2]
[1, 2, 1, 2, 1, 3]
[1, 2, 1, 2, 3, 1]
[1, 2, 1, 3, 1, 2]
[1, 2, 1, 3, 2, 1]
[1, 2, 2, 1, 1, 3]
[1, 2, 2, 1, 3, 1]
[1, 2, 2, 3, 1, 1]
[1, 2, 3, 1, 1, 2]
[1, 2, 3, 1, 2, 1]
[1, 2, 3, 2, 1, 1]
[1, 3, 1, 1, 2, 2]
[1, 3, 1, 2, 1, 2]
[1, 3, 1, 2, 2, 1]
[1, 3, 2, 1, 1, 2]
[1, 3, 2, 1, 2, 1]
[1, 3, 2, 2, 1, 1]
[2, 1, 1, 1, 2, 3]
[2, 1, 1, 1, 3, 2]
[2, 1, 1, 2, 1, 3]
[2, 1, 1, 2, 3, 1]
[2, 1, 1, 3, 1, 2]
[2, 1, 1, 3, 2, 1]
[2, 1, 2, 1, 1, 3]
[2, 1, 2, 1, 3, 1]
[2, 1, 2, 3, 1, 1]
[2, 1, 3, 1, 1, 2]
[2, 1, 3, 1, 2, 1]
[2, 1, 3, 2, 1, 1]
[2, 2, 1, 1, 1, 3]
[2, 2, 1, 1, 3, 1]
[2, 2, 1, 3, 1, 1]
[2, 2, 3, 1, 1, 1]
[2, 3, 1, 1, 1, 2]
[2, 3, 1, 1, 2, 1]
[2, 3, 1, 2, 1, 1]
[2, 3, 2, 1, 1, 1]
[3, 1, 1, 1, 2, 2]
[3, 1, 1, 2, 1, 2]
[3, 1, 1, 2, 2, 1]
[3, 1, 2, 1, 1, 2]
[3, 1, 2, 1, 2, 1]
[3, 1, 2, 2, 1, 1]
[3, 2, 1, 1, 1, 2]
[3, 2, 1, 1, 2, 1]
[3, 2, 1, 2, 1, 1]
[3, 2, 2, 1, 1, 1]
答えを言ってしまうと、「末尾から要素を見ていって初めて減少する位置」までが変化する。例えば a = [1, 2, 2, 3, 1, 1] の次は [1, 2, 3, 1, 1, 2] だが、
-
a[2] < a[3] >= a[4] >= a[5]のため、これらの要素が変化(置換)する。- 手前の
a[0..1]はそのまま。 - 見方を変えると、
a[3..-1]の部分的な順列は辞書順の最後になっていて、これらだけを置換するのでは次の順列は作れない。
- 手前の
-
a[2]をひとつ進めることになり、a[3..-1]からより大きい要素を探して採用する。 -
a[3..-1]は、残った要素で作れる辞書順先頭の順列を採用する。-
a[3..-1]が降順でソートされていれば、列を反転させるだけで済む。
-
これは自然数の繰り上がりと似ている。例えば十進数で 9599 の次は 9600 であり、
- 末尾から見て初めて
9でない桁が +1 され、 - それ以降は
00と最小のものにリセットされる。
(もっとも、繰り上がりは下の桁から順に処理していけるので、こんな方法をとる必要は無い。)
実装
レシーバーの配列を破壊的に変更する Array#next_permutation! を実装する。「次」が無い場合は nil を返す(中身は先頭の順列に変更する)ようにして、whileループなどで終了判定できるようにする。
アルゴリズム自体はin-placeでできるものの、列の反転を要素毎のswapで書くのは大変なので、一時的に部分配列を作っている。
class Array
def next_permutation!
return nil if self.empty?
prev = self.last
i = self.rindex { |ai| ai < prev || (prev = ai; false) }
unless i
self.reverse!
return nil
end
key = self[i]
j = self.rindex { |aj| aj > key }
self[i], self[j] = self[j], self[i]
self[i+1..-1] = self[i+1..-1].reverse!
return self
end
end
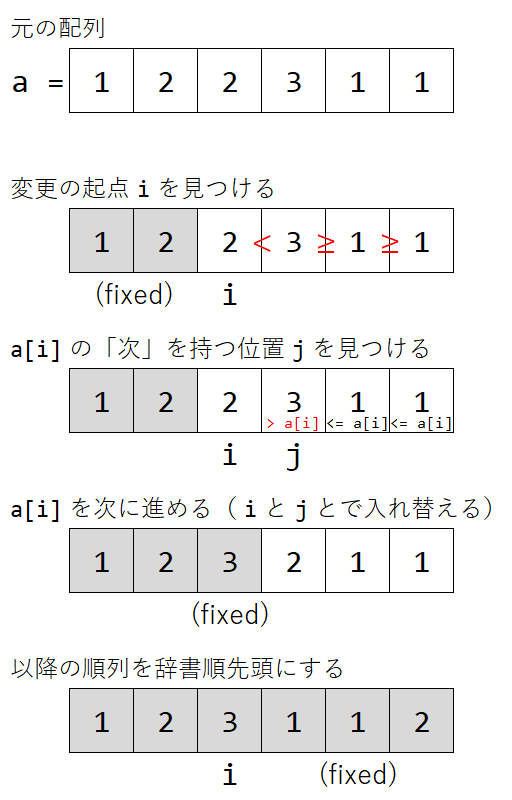
前節で例に挙げた a = [1, 2, 2, 3, 1, 1] に適用すると、下図のように動作する。
細かい注意点として、「 i と j とで入れ替える」とき、入れ替えた後も降順ソートが保たれている必要がある(最後でソートの代わりに反転を使うため)。もし a[i] の次(例では 3 )が複数あったら、一番右側を選んで入れ替えるようにすればうまくいく。元が降順なので普通に右から探索すれば罠にはハマらないが、凝った探索をする気なら注意がいる。
同様の考え方で、前の順列を求める prev_permutation も作れる。単に不等号の向きを逆転させればいい(等号の有無は変えないこと)。
参考
- LeetCode 31: Next Permutation - 今日も窓辺でプログラム
- next_permutation - cpprefjp C++日本語リファレンス
- 重複置換 - Wikipedia
-
辞書順での比較は、2つの列の要素を先頭から比較していき、初めて不一致だったときにその大小関係が採用される(例: "abcd" < "abd" )。不一致が列の終端に着いたためなら、列の短いほうが小さい(例: "abc" < "abcd" )。 c.f. [`Array#<=>`](https://docs.ruby-lang.org/ja/latest/method/Array/i/=3c=3d=3e.html) ↩