pythonで幅優先探索を実装をしてみた（キュー、描画自作）

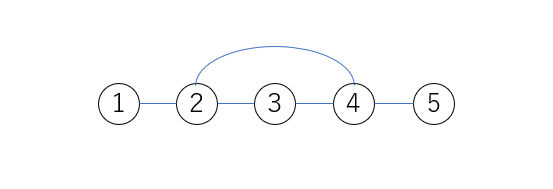
#幅優先探索（BFS）が必要になった場面（前置き）
Atcoderで木構造のグラフで内の２点の最短距離を求める問題に遭遇。
当時は自力でアルゴリズムを作成したが、問題が解ききれなかったため、BFSをきちんと作ってみることにした。
実際に使う際は、便利なライブラリを使わせてもらうとして、
今回は基本的な考え方をプログラミングして整理する。
ライブラリの使った実装し直しはまた後日。

※前回までで、木構造のクラスと描画プログラムを作った。
pythonで自前のグラフ構造のクラスとその描画を作る

※BFSについて以下の記事が詳しくまとめてあったので、参考にさせていただきました。
[BFS (幅優先探索) 超入門！ 〜 キューを鮮やかに使いこなす 〜]
(https://qiita.com/drken/items/996d80bcae64649a6580)

#実装
前置きはよいので以下実装。
##グラフ構造のクラス定義

#グラフ構造の作成
class cglaph():
  def __init__(self):
    #ノードの初期化
    self.nodes={}

  def addnode(self,num):#①ノードを追加
    for i in self.nodes.keys():
      if i==num:
        return(False)
    else:
      self.nodes[num]=list()
      return(True)

  def addedge(self,ag1,ag2):#②エッジを追加
    node1=min(ag1,ag2)
    node2=max(ag1,ag2)
    addok=False

    for i in self.nodes.keys():
      if i==node1:
        for j in self.nodes.keys():
          if j==node2:
            addok=True

    if addok:
      self.nodes[node1].append(node2)
      self.nodes[node2].append(node1)

  def printnodes(self):    #③ノードを表示
    print("■Glaph:")
    print("vertice:neighbors")
    for k,v in self.nodes.items():
      print(k,":",v)


  def getnodes(self):#④ノードのリストを返す
    keylist=list()

    for i in self.nodes.keys():
      keylist.append(i)
    return keylist

  def getedge(self, node):#⑤指定ノードのエッジ（つながっているノード）を返す。
    return self.nodes[node]

####今回のツリー構造のクラスの構想
ノードの情報は辞書型で保持する。keyにノード番号、valueにそのノードに繋がるノードをリストで格納する。
以下のメソッドを入れる。
①ノードの追加
②エッジの追加
③ノード（とそれとつながるノード）の表示
④ノードのリストを返す
⑤指定ノードに繋がるノードのリストを返す

##キュー構造のクラス定義

#キュー構造の定義
class cqu():
  def __init__(self):
    #キューの初期化
    self.qu=list()
    self.head=0
    self.tail=-1

  def quval(self):#①キューの大きさ
    return self.tail-self.head+1

  def printqu(self):#②キューの中身表示
    print(str(self.qu[self.head:self.tail+1])+",head:"+str(self.head)+",tail:"+str(self.tail))
    print(self.qu)

  def enqu(self,num):#③エンキュー
    self.qu.append(num)
    self.tail+=1
 
  def dequ(self):#④デキュー
    if self.quval()!=0:
      outv=self.qu[self.head]
      self.head+=1
      return outv

    else:
      return False

####キュー構造クラスの構想
キューはリスト構造とし、先頭、後尾を示すポインタのような変数を持つこととする。
以下のメソッドを持たせる。
①キューの大きさを返す
②キューの中身を表示
③エンキュー
④デキュー

##木構造の作成

G=cglaph()

G.addnode(1)#ノードの追加
G.addnode(2)
G.addnode(3)
G.addnode(4)
G.addnode(5)
G.addedge(1,2)#エッジの追加
G.addedge(2,3)
G.addedge(3,4)
G.addedge(4,5)
G.addedge(2,4)
G.printnodes()#ノードの一覧表示

nodelist=G.getnodes()#ノードリストを取得
print ("NODE LIST:",nodelist)

G.getedge(1)#ノード１とつながっているノード

イメージは以下のグラフ

※グラフ描画の際のノードの座標は
BFSで探索開始ノードからの距離を使うことでいくらかマシになるので、最後に描画することにする。

##BFSの実装

StartNode=1

#対象グラフG
G.printnodes()

#距離を記録するリスト
NodeList=G.getnodes()
#print(NodeList)
DistList=[0]*len(NodeList)

#キュー構造生成
Q=cqu()

#①探索開始ノードをエンキュー
Q.enqu(StartNode)
#Q.printqu()

while Q.quval():#②キューの大きさが０になるまでループ
  #print("=====loop=====")
  #Q.printqu()
  #print("Qval"+str(Q.quval()))

  checknode=Q.dequ()#③デキュー
  #print("deQ:"+str(checknode))

  nextnodes=G.getedge(checknode)#④エンキューで取得したノードとつながるノードを取得
  #print("next nodes:"+str(nextnodes))

  for i in nextnodes:#⑤つながっている各ノードに距離を与える
    #print(i)
    if DistList[NodeList.index(i)]==0:#⑥探索済み（ノードに距離を与え済み）か判定
      if i!=StartNode:#⑦探索開始ノードは対象外
        #print("enq")
        Q.enqu(i)#⑧エンキュー、未探索であれば距離を与える（探索済みにする）
        DistList[NodeList.index(i)]=DistList[NodeList.index(checknode)]+1#⑨探索もとのノードから距離を＋１
    
    #print(DistList)

print("距離リスト",DistList)

単純な実装であれば、他サイトにいくらでもあるので、あえて作成中のデバッグ用コメントは残してあります。

アルゴリズムとしては、デキューして出発ノードを決定。出発ノードとつながっているノードをエンキュー。を繰り返す。

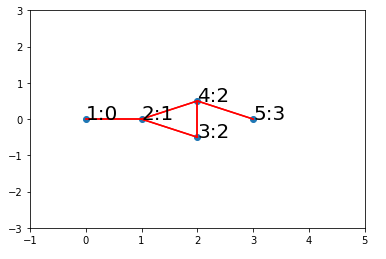
##グラフと探索結果の描画

import matplotlib.pyplot as plt
import collections
import copy

#探索距離に応じたグラフの描画
N=len(nodelist)
x=DistList#x座標は距離
y=[0]*N#Y座標は、X座標が同じノードを等間隔で配置（以下で等間隔を求める）===
c=collections.Counter(DistList)#重複する要素の数を求める。
tmp=c.most_common()

c2=collections.Counter(DistList)#修正用カウンター


tmpmean=copy.deepcopy(tmp)
for i in range(len(tmp)):
  tmpmean[i]=(c[i]-1)*0.5+1


for i,n in zip(DistList,range(N)):
  if c[i]!=1:#1はy=0ライン
    y[n]=-c2[i]+tmpmean[i]
    c2[i]-=1
#===ここまでx,y座標を求めたいだけ

print("x:",x)
print("y:",y)

#グラフ作成
plt.figure(1)

#ノード描画
plt.scatter(x,y)

#ノード位置にノード名を付ける
ax=plt.axes()
for i in range(N):
  ax.annotate(str(nodelist[i])+":"+str(DistList[i]),(x[i],y[i]),size=20)

#エッジを描画
for i in nodelist:
  edges=G.getedge(i)
  for j in edges:
    plt.plot((x[nodelist.index(i)],x[nodelist.index(j)]),(y[nodelist.index(i)],y[nodelist.index(j)]), color='red')


plt.xlim(-1, 5)
plt.ylim(-3, 3)

各ノードについたアノテーションは(ノード番号：探索開始ノードからの距離)としている。

###まとめ、今後の課題
・BFS自体は、キュー構造を使用して簡単に実装可能である。
・実践を見据えてライブラリを利用した実装を今後まとめる。
・距離が同じ（同一階層）ノードが複数連続で続くと、グラフがねじれる現象が発生する。グラフ描画アルゴリズムを調べる。

###参考文献
BFS (幅優先探索) 超入門！ 〜 キューを鮮やかに使いこなす 〜

[グラフ描画アルゴリズムとNetworkxの裏側]
(https://qiita.com/odanny/items/7c550010f5915ae4acdc)

pythonで自前のグラフ構造のクラスとその描画を作る

とっても便利なPythonの辞書型について覚え書き

PythonのCounterでリストの各要素の出現個数をカウント