はじめに
こんにちは、事業会社で働いているデータサイエンティストです。
本記事では、Chernozhukov and Hong(2003)が提案した手法に基づき、ベイズ的な枠組みで一般化モーメント法(GMM, Generalized Method of Moments)のモデルを推定する方法を、Stan言語による実装例とともに解説します。
一般化モーメント法は、計量経済学や政治学方法論といった限られた分野で主に用いられており、一般のデータサイエンス分野ではあまり知られていません。そこで本記事では、幅広い読者にご理解いただけるよう、まずはGMMとその原型であるモーメント法(MM, Method of Moments)の概要から丁寧に説明します。
個人的に、Chernozhukov and Hong(2003)の提案したこの手法には非常に大きな魅力を感じています。しかし、実際の実証分析ではあまり使われておらず、公開されている実装コードも見当たりません。そのため、本記事で紹介するStanコードについては、理論的な整合性に細心の注意を払ってはおりますが、万が一誤りが含まれている可能性もあります。あらかじめご留意いただければ幸いです。
それでもなお、この優れたモデリング手法を広く共有することで、データサイエンスが提供できる価値をさらに高めていきたいと考えています。
もし本記事の内容やコードに誤りや改善点などがございましたら、ぜひご指摘・コメントをいただけますと幸いです。
モーメント法とは
さて、いきなりですが、データサイエンスの基本として、最小二乗法によって線形回帰モデルのパラメータを解析的に求める手順を覚えていますか?
まず、以下のような線形回帰モデルを仮定します。ここで、$y$ は $N$ 次元の従属変数ベクトル、$X$ は $N \times K$ 次元の独立変数行列、$\epsilon$ はモデルで説明できないノイズを表す $N$ 次元の誤差項です:
$$
y = X\beta + \epsilon
$$
つまり、「独立変数 $X$ と係数 $\beta$ の内積に、誤差 $\epsilon$ を加えることで従属変数 $y$ を表現する」という構造です。
それでは、$\beta$ はどのように求めればよいでしょうか?
最小二乗法では、ノイズ項 $\epsilon$ の平方和が最小になるような $\beta$ を求めます。すなわち、以下の目的関数を最小化します:
$$
\min_\beta \ \epsilon' \epsilon
$$
これを $y$ と $X$ を用いた形に書き換えると、
$$
\min_\beta \ (y - X\beta)'(y - X\beta)
$$
となります。
詳細な導出は省略しますが、この目的関数を $\beta$ について微分し、導関数をゼロとおくことで、次のような解析解が得られます:
$$
\hat{\beta} = (X'X)^{-1}X'y
$$
これが、最小二乗法によって得られる回帰係数の解析的な解です。
ただ、実はこの解析解 $\hat{\beta} = (X'X)^{-1}X'y$ は、最小二乗法だけでなく、モーメント法による解としても解釈することができます。
モーメント法では、ノイズ項の平方和を最小化するのではなく、独立変数 $X$ と誤差項 $\epsilon$ が無相関であるという性質に着目します。具体的には、次のモーメント条件を仮定します:
$$
\mathbb{E}[X'\epsilon] = 0
$$
この式を少し丁寧に展開してみましょう:
$$
\mathbb{E}[X'(y - X\beta)] = 0
$$
$$
\mathbb{E}[X'y] - \mathbb{E}[X'X\beta] = 0
$$
$$
\mathbb{E}[X'y] = \mathbb{E}[X'X]\beta
$$
両辺に $\mathbb{E}[X'X]^{-1}$ をかけると:
$$
\beta = (\mathbb{E}[X'X])^{-1} \mathbb{E}[X'y]
$$
ここで、$\mathbb{E}$ を無視して標本値で置き換えると:
$$
\hat{\beta} = (X'X)^{-1}X'y
$$
なんと、不思議なことに、これはまさに最小二乗法で導かれた解析解と同じ式になります。
このように、最小二乗法とモーメント法は異なるアプローチに基づきながらも、同じ解に到達します。
このように、モーメント法は「AとBに相関がない」といった非常に弱い仮定のもとで、パラメータを推定する手法を提供してくれます。たとえば、ここまでの説明では、誤差項 $\epsilon$ が正規分布に従うといった分布に関する仮定を一切置いていません。
さらに、たとえば内生性の問題により $X$ と $\epsilon$ の間に相関がある場合でも、$\epsilon$ と相関のない別の変数 $Z$(=操作変数)が見つかれば、
$$
\mathbb{E}[Z'\epsilon] = 0
$$
というモーメント条件を利用して、$\beta$ を推定することが可能です。
より一般に、経済理論が提供してくれるのは、確率分布の完全な形式ではなく、モーメント条件のみであることが多いという点も重要です。
たとえば、Jagannathan, Skoulakis, and Wang(2002)においては、次のようなモーメント条件が示されます:
- $\beta$:異時点間の割引因子
- $c_t$:$t$期の消費
- $\gamma$:リスク回避度
- $R_{i,t}$:$t$期の資産$i$の総収益
- $I_t$:$t$期の情報集合
このとき、理論的には次のモーメント条件が成立するとされています:
$$
\mathbb{E} \left[\beta \left( \frac{c_{t+1}}{c_t} \right)^{-\gamma} R_{i,t+1} \middle| I_t \right] = 1
$$
これも先ほどの $\mathbb{E}[X'\epsilon] = 0$ と同様、モーメント条件の一種です。
情報集合 $I_t$ に含まれる変数を $K$ 次元のベクトル $z$ とすれば、次のように $K$ 本のモーメント条件を導くことができます:
$$
\mathbb{E} \left[ \left( 1 - \beta \left( \frac{c_{t+1}}{c_t} \right)^{-\gamma} R_{i,t+1} \right) z_1 \right] = 0
$$
$$
\mathbb{E} \left[ \left( 1 - \beta \left( \frac{c_{t+1}}{c_t} \right)^{-\gamma} R_{i,t+1} \right) z_2 \right] = 0
$$
$$
\mathbb{E} \left[ \left( 1 - \beta \left( \frac{c_{t+1}}{c_t} \right)^{-\gamma} R_{i,t+1} \right) z_3 \right] = 0
$$
(途中略)
$$
\mathbb{E} \left[ \left( 1 - \beta \left( \frac{c_{t+1}}{c_t} \right)^{-\gamma} R_{i,t+1} \right) z_k \right] = 0
$$
このようにして、$k$ 本のモーメント条件が得られます。
ただし、これらの条件は線形回帰のように単純な式変形では解けません。そこで登場するのが、一般化モーメント法です。
一般化モーメント法では、観測単位 $i$ に対して得られる $k$ 次元のモーメントベクトルを
$$
m_i(\theta)
$$
と表し、ここで $\theta$ はすべての推定パラメータを含むベクトルです。
一般化モーメント法は以下の目的関数を最小化する $\theta$ を推定します:
$$
\max_{\theta} \ -0.5 \left( \frac{1}{\sqrt{n}} \sum_{i=1}^{n} m_i(\theta) \right)' W_n(\theta) \left( \frac{1}{\sqrt{n}} \sum_{i=1}^{n} m_i(\theta) \right)
$$
これは Chernozhukov and Hong(2003)の Example 3 で紹介されている形式です。ここで $W_n(\theta)$ は、ウエイト行列であり、理論上は効率性を高めるための役割を果たします。
ベイズ版モーメント法の概念
このように、一般化モーメント法は、ノイズ項の分布に関する仮定を一切置かずに、理論が示すモーメント条件をそのまま純粋に推定に活かせる点が、大きな魅力の一つです。
ただし、一般化モーメント法の目的関数:
$$
L_n(\theta) = -0.5 \left( \frac{1}{\sqrt{n}} \sum_{i=1}^n m_i(\theta) \right)' W_n(\theta) \left( \frac{1}{\sqrt{n}} \sum_{i=1}^n m_i(\theta) \right)
$$
には、確率分布に関する情報が一切含まれていないため、通常のベイズ的推定(MCMCや変分推論)を適用することができません。
しかし、たとえば先述した経済モデルを銀行が実務で利活用する場合を考えてみましょう。
現実には、すべての顧客 $u$ が同じリスク回避度 $\gamma$ を持つとは考えにくく、顧客ごとに異なる $\gamma_u$ を仮定した方が、パーソナライズされた金融商品の推薦(リスクの高い資産を誰に勧めるか等)においてはるかに有効です。このように:
$$
\mathbb{E} \left[\beta \left( \frac{c_{t+1}}{c_t} \right)^{-\gamma_u} R_{i,t+1} \middle| I_t \right] = 1
$$
のようなパラメータの異質性を考慮することが、意思決定や収益の最大化において重要となります。
こうした異質性の推定には階層ベイズモデルが有効ですが、一般化モーメント法の目的関数はベイズ推定と整合しないため、そのままでは利用できないという欠点があります。
ここで登場するのが、Chernozhukov and Hong(2003)による革新的な提案です。
彼らは、一般化モーメント法の目的関数 $L_n(\theta)$ を次のように変形することで、擬似的な事後分布を定義しました:
$$
p_n(\theta) = \frac{e^{L_n(\theta)} \pi(\theta)}{\int_{\Theta} e^{L_n(\theta)} \pi(\theta) d\theta}
$$
ここで、$\pi(\theta)$ は $\theta$ に対する事前分布を表します。
この $p_n(\theta)$ を、擬似事後分布とみなすことで、MCMCなどのベイズ的推定手法を適用可能にするというのが彼らの主張です。
この手法により、一般化モーメント法の柔軟性とベイズ推定の表現力を両立させることができ、パラメータの異質性を扱う階層モデリングへの応用も視野に入ってきます。
Stanによる実装に入る前に、階層モデリングへの応用はあくまでも筆者が強く感じた可能性であり、Chernozhukov and Hong(2003)の問題意識ではないことを強調しておきたいです。Chernozhukov and Hong(2003)はMCMCによる効率的な計算を目的としています。
Stanの実装コード
さて、Stanでこのモデルを実装するには、私たちは何をすればよいのでしょうか?
まずは、擬似事後分布の式をもう一度確認しておきましょう:
$$
p_n(\theta) = \frac{e^{L_n(\theta)} \pi(\theta)}{\int_{\Theta} e^{L_n(\theta)} \pi(\theta) d\theta}
$$
Stanは、分母の正規化定数(積分項)をよしなに処理してくれるため、私たちが注目すべきは次の比例関係です:
$$
p_n(\theta) \propto e^{L_n(\theta)} \pi(\theta)
$$
事前分布 $\pi(\theta)$ が正規分布である場合は、Stanでいつも通り以下のように書けば問題ありません(theta ~ normal(0, 1);)。
問題となるのは $e^{L_n(\theta)}$ の部分です。Stanには、一般化モーメント法の目的関数に指数関数を適用した項を直接扱うビルトイン関数は存在しないため、これを自分で target に明示的に加える必要があります。
ここで重要なのは、Stanの target は対数尤度を構築するための変数であるという点です。したがって、次のように対数を取った形で考える必要があります:
$$
log(p_n(\theta)) \propto log(e^{L_n(\theta)}) + log(\pi(\theta))
$$
$$
log(p_n(\theta)) \propto L_n(\theta) + log(\pi(\theta))
$$
つまり、一般化モーメント法の目的関数 $L_n(\theta)$ をそのまま target に加えればよいということになります。
まとめると、Stanでこのモデルを実装する際には:
-
事前分布 $\pi(\theta)$ を通常通り
~構文で指定する -
一般化モーメント法の目的関数 $L_n(\theta)$ を
target +=を使って加える
という2点を押さえれば、擬似ベイズ的な推定が可能になります。
Stanでの実装はこちらです。モーメント法とはのところで説明した操作変数の例を実装しました:
$$
\mathbb{E}[Z'\epsilon] = 0
$$
$$
\mathbb{E}[Z'(y - X \beta)] = 0
$$
モーメント条件は一つしかないため、$W_{n}(\theta)$ を1にすると、目的関数は
$$
L_{n}(\beta) = \ -0.5 \left ( \frac{1}{\sqrt{n}} \sum_{i = 1}^{n} z_i'(y_i - x_i' \beta) \right) ^2
$$
になります。
data {
int N;
vector[N] z;
vector[N] x;
vector[N] y;
}
parameters {
real intercept;
real beta;
}
model {
intercept ~ normal(0, 10);
beta ~ normal(0, 10);
vector[N] moment;
for (i in 1:N){
moment[i] = (1/sqrt(N)) * (y[i] - (intercept + x[i] * beta)) * z[i];
}
target += - 0.5 * sum(moment)^2;
}
シミュレーション分析
ここではまず、内生性がある状態のデータを生成して、変分推論を用いてモデル推定します。パラメータの正解は -0.6 です。
set.seed(123456)
df <- 10000 |>
mvtnorm::rmvnorm(c(0, 0), sigma = matrix(c(1, 0.8, 0.8, 1), nrow = 2)) |>
tibble::tibble(
e = _
) |>
dplyr::mutate(
e_1 = e[,1],
e_2 = e[,2],
z = rnorm(dplyr::n()),
x = 0.9 * z + e_1,
y = - 0.6 * x + e_2
)
m_gmm_init <- cmdstanr::cmdstan_model("gmm.stan")
m_gmm_estimate <- m_gmm_init$variational(
data = list(
N = nrow(df),
z = df$z,
x = df$x,
y = df$y
)
)
m_gmm_summary <- m_gmm_estimate$summary()
結果を確認しましょう:
> m_gmm_summary
# A tibble: 4 × 7
variable mean median sd mad q5 q95
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 lp__ -30.5 -29.1 11.8 11.0 -52.1 -13.8
2 lp_approx__ -0.980 -0.688 1.00 0.707 -2.89 -0.0456
3 intercept -0.0142 -0.00163 1.07 1.13 -1.75 1.69
4 beta -0.522 -0.522 0.0149 0.0144 -0.546 -0.497
$\beta$ の推定値は-0.522で、悪くはなさそうです。念の為、内生性のある状態で利用できない最小二乗法をあえて使うと:
> df |>
lm(y ~ x, data = _) |>
summary()
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.9848 -0.5491 -0.0045 0.5541 3.0172
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.011661 0.008050 1.449 0.147
x -0.161481 0.005992 -26.949 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.805 on 9998 degrees of freedom
Multiple R-squared: 0.06772, Adjusted R-squared: 0.06763
F-statistic: 726.2 on 1 and 9998 DF, p-value: < 2.2e-16
-0.16でかなり外れていますね、、、
ではR言語の ivreg で頻度論の普通の操作変数法はどうでしょうか?
> df |>
ivreg::ivreg(y ~ x | z, data = _) |>
summary()
Call:
ivreg::ivreg(formula = y ~ x | z, data = df)
Residuals:
Min 1Q Median 3Q Max
-4.206645 -0.665584 0.002087 0.660057 3.527035
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.014614 0.009942 1.47 0.142
x -0.595722 0.010979 -54.26 <2e-16 ***
Diagnostic tests:
df1 df2 statistic p-value
Weak instruments 1 9998 8325 <2e-16 ***
Wu-Hausman 1 9997 7772 <2e-16 ***
Sargan 0 NA NA NA
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9942 on 9998 degrees of freedom
Multiple R-Squared: -0.422, Adjusted R-squared: -0.4221
Wald test: 2944 on 1 and 9998 DF, p-value: < 2.2e-16
お!-0.59でかなりいい感じです!
ただし、一度のシミュレーション結果だけで評価するのは適切とは言えません。そこで、Stanモデルによるベイズ推定量、最小二乗法による推定量、頻度論的操作変数法による推定量の頻度論的分布を生成し、それらを比較することにします。
──あ、そうです。ベイズ推定量にも頻度論的分布は定義できます。ちょっと気持ち悪いですよね笑。もちろん、ベイズ推定を強く支持する方もいらっしゃるかもしれませんが、残念ながら私は頻度論のほうがより一般性が高いと考えています。もしこの点に関心がある方は、Efron(2015)などの議論をぜひ読んでみてください。
future::plan(future::multisession)
simple_simulation_result <- 1000 |>
seq_len() |>
furrr::future_map(
\(i){
df <- 10000 |>
mvtnorm::rmvnorm(c(0, 0), sigma = matrix(c(1, 0.8, 0.8, 1), nrow = 2)) |>
tibble::tibble(
e = _
) |>
dplyr::mutate(
e_1 = e[,1],
e_2 = e[,2],
z = rnorm(dplyr::n()),
x = 0.9 * z + e_1,
y = - 0.6 * x + e_2
)
m_gmm_estimate <- m_gmm_init$variational(
data = list(
N = nrow(df),
z = df$z,
x = df$x,
y = df$y
)
)
bayesian_gmm_beta <- m_gmm_estimate$summary() |>
dplyr::filter(variable == "beta") |>
dplyr::pull(mean)
freq_iv_beta <- ivreg::ivreg(y ~ x | z, data = df) |>
coef() |>
purrr::pluck(2)
freq_ols_beta <- lm(y ~ x, data = df) |>
coef() |>
purrr::pluck(2)
return(
list(
bayesian_gmm_beta = bayesian_gmm_beta,
freq_iv_beta = freq_iv_beta,
freq_ols_beta = freq_ols_beta
)
)
},
.progress = TRUE,
.options = furrr::furrr_options(seed = 12345)
)
結果を可視化しましょう:
simple_simulation_result |>
dplyr::bind_rows() |>
dplyr::mutate(
rid = dplyr::row_number()
) |>
tidyr::pivot_longer(!rid, names_to = "estimator", values_to = "value") |>
dplyr::filter(dplyr::between(value, -5, 5)) |>
ggplot2::ggplot() +
ggplot2::geom_density(ggplot2::aes(x = value, fill = estimator), alpha = 0.5) +
ggplot2::geom_vline(xintercept = -0.6, linetype = "dashed") +
ggplot2::scale_fill_manual(
values = c(
"bayesian_gmm_beta"="red",
"freq_iv_beta"="blue",
"freq_ols_beta"="yellow"
)
)
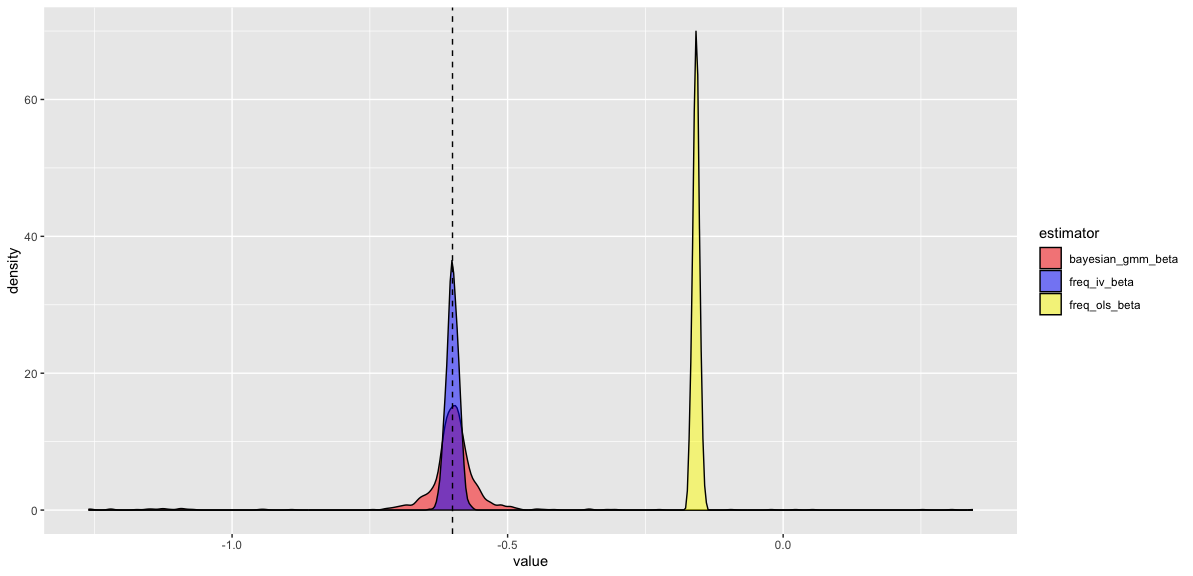
最小二乗法(freq_ols_beta)は、常に大幅に外れていて、そもそも正解である-0.6を中心に分布していません。本記事が実装したChernozhukov and Hong(2003)の提案手法(bayesian_gmm_beta)と頻度論の普通の操作変数法(freq_iv_beta)は正解の-0.6を中心に分布していますが、分散は頻度論の普通の操作変数法の方が低いです。
結論
いかがでしたか?このように、一般化モーメント法をベイズ推定によって扱う手法は、十分に機能する可能性があることが示唆されました。さらに、この枠組みに階層ベイズ構造を組み込むことで、ビジネス上重要なパーソナライズ・レコメンデーションの基盤としても応用できるのではないかと考えています。
今後の記事では、より複雑な一般化モーメント法モデルをどのようにベイズ的に拡張していくかについても紹介していく予定です。
最後に、私たちと一緒に働きたい方はぜひ下記のリンクもご確認ください:
参考文献
Chernozhukov, Victor, and Han Hong. "An MCMC approach to classical estimation." Journal of econometrics 115.2 (2003): 293-346.
Efron, Bradley. "Frequentist accuracy of Bayesian estimates." Journal of the Royal Statistical Society Series B: Statistical Methodology 77.3 (2015): 617-646.
Jagannathan, Ravi, Georgios Skoulakis, and Zhenyu Wang. "Generalized methods of moments: Applications in finance." Journal of Business & Economic Statistics 20.4 (2002): 470-481.