はじめに
こんにちは、事業会社で働いているデータサイエンティストです。
今回の記事では、ミクロ経済学の効用最大化理論と、ミクロ計量経済学の離散選択理論を用いて、word2vec におけるネガティブサンプル(正解ではない単語を抽出して学習データに混ぜる手法)を正当化し、さらに高速化する方法を紹介します。
少し集合論的な議論も出てきますが、ここで強調したいのは、
- 「機械学習モデルをミクロ経済学で解釈できた!わーい!」
- 「機械学習モデルを圏論で解釈できた!わーい!」
といったスタンスは誤りだということです。
「深層学習を圏論的に解釈できた!」——で?このような数学遊びにとどまっては、実証分析者として意味がありません。大切なのは、理論と結びつけることでどんなメリットが得られるのかを明示することです。
本記事で示すポイントは、ネガティブサンプルを「文脈を見て、最も高い効用をもたらす単語を選ぶ」という効用最大化行動として位置づけられることです。これにより、正解データとネガティブサンプルデータを同じレコードに含められるようになり、結果として複雑な内積計算の回数を削減でき、学習の高速化につながります。
また、本記事ではアイデアの説明を中心にしているため、文献の引用は省略される場合があります。ミクロ経済学の理論に興味のある方は Varian(1992)を、離散選択理論を中心とするミクロ計量経済学の理論については Train(2009)を参照してください。
では早速説明に入りたいと思います!
話者の単語選好
ここからはかなりミクロ経済学っぽくなりますが、自然言語処理などの他分野の方にも理解していただけるように、できるだけ丁寧に説明します。
まず、次の文の X に最も適切な、すなわち日本語話者にとって最も「しっくりくる」(満足度の高い)単語を入れる問題を考えましょう:
戦争は X の失敗である
話者は、「戦争は」と「の失敗である」という前後の文脈をもとに、日本語のすべての単語を「しっくりくる」感の順に並べ、$\succeq$ という記号で選好(preference)を表します。例えば、
$$
\text{外交} \succeq \text{チーズ}
$$
とは、この文脈で「外交」を X に入れるのは、「チーズ」を入れるよりも望ましい(あるいは同等に望ましい)ことを意味します。もちろん実際には、この文脈で「チーズ」が「外交」と同等になることはあり得ないので、実際は $\succ$(「外交」がより好ましい)が成立するでしょう。
さて、この選好関係 $\succeq$ に対して、次の3つの条件を課すと、その選好は「合理的」であるといいます:
-
完備性(completeness)
日本語の語彙に属するすべての単語 $x, y$ について、必ず $x \succeq y$ または $y \succeq x$ が成立する。
→ あらゆる2つの単語は比較可能であり、話者が「どちらがより文脈に合うか」を必ず判断できることを意味します。 -
反射性(reflexiveness)
日本語の語彙に属するすべての単語 $x$ について、常に $x \succeq x$ が成立する。
→ 少なくとも自分自身とは同等に望ましい、と定義することで、選好関係が矛盾なく始まることを保証します。 -
推移性(transitivity)
日本語の語彙に属するすべての単語 $x, y, z$ について、もし $x \succeq y$ かつ $y \succeq z$ ならば、必ず $x \succeq z$ が成立する。
→ 文脈への「しっくりくる」感が論理的に一貫することを保証し、循環的な好み($x \succ y \succ z \succ x$ のような矛盾)が生じないようにします。
これらの条件を満たすと、話者の単語選択は「効用最大化」として整合的に記述できます。すなわち、
- 完備性により、話者は常に文脈に対して「どの単語がより適切か」を比較可能です。
- 反射性により、同じ単語を比較しても矛盾が生じません。
- 推移性により、単語間の選好は循環せず、一貫した「最も望ましい単語」を選び出すことが可能です。
これが自然言語処理の観点で重要なのは、「文脈に基づく単語の選択」が経済学的な合理的選好として定式化できることです。つまり、word2vec における「正解単語」と「ネガティブサンプル単語」の比較は、まさにこの合理的選好の枠組みの中で正当化されるのです。
さらに、4つ目の条件
-
連続性(continuity)
日本語の語彙に属するすべての単語 $y$ について、{$ x : x \succeq y $} と {$ x : y \succeq x $} は閉集合である
も満たされれが、日本語のすべての単語を「しっくりくる」感の順は効用関数の相対的な大きさで表現できることが知られています。
連続性条件は、選好関係を効用関数で表現できるために重要な仮定のひとつです。直感的には「しっくりくる」順が急に飛び跳ねることなく、少しずつ変化することを保証しています。
もし連続性が成り立たなければ、ある単語 $y$ に対して「それ以上にしっくりくる」単語の集合や「それ以下の単語の集合」が不連続になり、効用関数で一貫して表すことが難しくなります。
つまり、連続性によって選好の構造が安定し、効用関数による滑らかな数値化が可能になるのです。
また、「しっくりくる」順は文脈によって異なりますので、$\succeq_{c}$ で文脈が $c$ になっている際の「しっくりくる」順を表します。
効用関数
さて、ここでは「しっくりくる」順序が完備性・反射性・推移性・連続性を満たすと仮定し、文脈 $c$ が与えられたときの「しっくりくる」感を効用関数で表現してみましょう:
$$
U_{word,c} = \alpha_{word} + \sum_{d=1}^{\infty} \left( \beta_{word,d} \cdot \delta_{d} \cdot \sum_{i \in c} \gamma_{i,d} \right) + \epsilon
$$
つまり、文脈 $c$ において単語 $word$ を選んだときの満足度(=「しっくりくる」感)は、単語固有の切片 $\alpha$ と、単語ベクトル $\beta$ と文脈ベクトル $\gamma$ の内積(ただし次元ごとに重み $\delta$ をかけて調整)で表現できる、ということです。これらのパラメータ、特に次元の重み $\delta$ の生成方法については後ほど説明します。最後に、分析者が観測できないノイズ項 $\epsilon$ は、例えば個々人の信念や経験、またはその場のただのノリ(?)によって「適切な単語」の感じ方が微妙に異なるような不確実性を表しています。ここでは分析者が把握できる効用関数の部分、$\alpha_{word} + \sum_{d=1}^{\infty} \left( \beta_{word,d} \cdot \delta_{d} \cdot \sum_{i \in c} \gamma_{i,d} \right)$ を $\bar{U_{word_c}}$ と置きます。
さて、ここで、ノイズ項が第1種極値分布に従うと仮定すると、単語 w が選ばれる確率は下記のようにかけることが知られています:
$$
P(word_{i} | c) = \frac{exp(\bar{U_{i_c}})}{\sum_{o \in 日本語の単語} exp(\bar{U_{o_c}})}
$$
まさに機械学習でお馴染みのソフトマックス関数ですね!そうです、これは完全にミクロ経済理論から導かれたものですが、今では word2vec にかなり近づいてきました!
ただ、このままだと、ソフトマックス関数の分母のため、日本語のすべての単語の $\bar{U_{i_c}}$ を計算する必要があり、膨大な計算リソースを使ってしまいます。ここで、ノイズ項が第1種極値分布に従う時の効用最大化アクターの行動の特徴である「無関連な対象からの独立性 (Independence of Irrelevant Alternatives: IIA)」の性質を利用します。
IIA の妥当性
まず、IIA とは何かを説明します。先ほどの「外交」と「チーズ」の例を使って、「外交」が「しっくりくる」単語として選ばれる確率と、「チーズ」が選ばれる確率の比率を計算してみましょう。
$$
P(外交|c) = \frac{exp(\bar{U_{外交_c}})}{\sum_{o \in 日本語の単語} exp(\bar{U_{o_c}})}
$$
$$
P(チーズ|c) = \frac{exp(\bar{U_{チーズ_c}})}{\sum_{o \in 日本語の単語} exp(\bar{U_{o_c}})}
$$
ここで、確率の比率を計算するために $P(外交|c)$ を $P(チーズ|c)$ で割ります:
$$
\frac{P(外交|c)}{P(チーズ|c)} = \frac{\frac{exp(\bar{U_{外交_c}})}{\sum_{o \in 日本語の単語} exp(\bar{U_{o_c}})}}{\frac{exp(\bar{U_{チーズ_c}})}{\sum_{o \in 日本語の単語} exp(\bar{U_{o_c}})}}
$$
お気づきの通り、$\sum_{o \in 日本語の単語} exp(\bar{U_{o_c}})$ は相殺されます。整理すると:
$$
\frac{P(外交|c)}{P(チーズ|c)} = \frac{exp(\bar{U_{外交_c}})}{exp(\bar{U_{チーズ_c}})}
$$
$$
\frac{P(外交|c)}{P(チーズ|c)} = exp(\bar{U_{外交_c}} - \bar{U_{チーズ_c}})
$$
そうなんです。外交とチーズだけを比較して、「戦争は X の失敗である」の X としてどちらが「しっくりくる」かを判断するとき、「正義」、「地政学」、「国際法」、「国際政治学現実主義」、「コーラ」、「ピザ」など他の単語は比率の計算に一切影響しません。この性質が無関連な対象からの独立性、IIAです。
IIAは妥当でしょうか?IIA(独立した選択肢の比率)の妥当性を考えるために、経済学で有名な「赤バス・青バス問題」を自然言語処理の文脈に置き換えてみましょう。
文脈 $c$ において、ある単語を選ぶとします。元々の選択肢は「外交」と「チーズ」の2つです。このとき、IIA が成り立つ場合、2つの単語の選択確率の比は、他の選択肢が追加・削除されても変わらないという性質を持っています。
$$
\frac{P(\text{外交}|c)}{P(\text{チーズ}|c)} \quad \text{は固定}
$$
「戦争は X の失敗である」の X に「外交」を選択する確率を 0.9、「チーズ」を選択する確率を 0.1 としましょう。ここで、新たに「ステーキ」という選択肢を追加した場合を考えます。おそらく、「外交」の選択確率はほとんど変わらず、一方で「ステーキ」と同じくらいふざけた「チーズ」(「戦争はステーキの失敗」ってどゆことw)は、それぞれ 0.05 になると想像するのが自然ではないでしょうか。
しかし、この場合、「ステーキ」が追加される前後で、$\frac{P(\text{外交}|c)}{P(\text{チーズ}|c)}$ は、もともと $\frac{0.9}{0.1} = 9$ だったものが、追加後には $\frac{0.9}{0.05} = 18$ に変わってしまいます。つまり、IIA が要求する「比率が固定」という条件を満たさなくなってしまうのです。
これは正直あまり直感的な帰結ではありませんが、機械学習系でソフトマックスを出力層として利用するモデルは、すべて暗黙的に IIA を仮定しています。層をいくら追加したとしても、最新のモデルアーキテクチャを使っていても、NVIDIA の GPU を使っていても、リーダブルなコードを書いていても、コードレビューをしていても、CI/CD をきちんと整備していても、この点は変わりません。ソフトマックスにはこの大前提が組み込まれており、ソフトマックスを利用する以上、逃れることはできないのです。
IIA を満たさない行動をモデリングする手法はミクロ計量経済学の分野で数多く開発されています。今後は、そうしたモデルを word2vec に応用した場合にどうなるかを比較検討する記事も執筆したいと考えていますが、本記事ではひとまず IIA の仮定を受け入れて、分析を進めます。
尤度関数
詳細は Train(2009)のページ 64~66 を参照していただきたいですが、まさにノイズ項が第1種極値分布に従う場合の効用最大化アクターの行動の特徴である IIA により、元々「外交」 vs 他のすべての日本語の単語の選択問題を、ランダムに選ばれた一部の単語との「外交」 vs その一部の単語の選択問題に置き換えることが可能です。そして、この一部の単語が分析者によってランダムに選択されていれば、パラメータの推定は一致性を保つことが知られています。つまり、「外交」 vs 広辞苑に収録されている全ての日本語の単語の選択問題を、「外交」 vs 「チーズ」の選択問題に置き換えても、情報は変わらないのです。
さて、ここで自然言語処理の専門家の方はお気づきかと思いますが、完全にミクロ経済理論しか使っていないにも関わらず、word2vec のネガティブサンプルの考え方に自然とたどり着きました。
さらに、ノイズ項が第1種極値分布に従う場合、二つの選択肢しかない離散選択問題において、選択肢 A の効用を $U_{A}$、選択肢 B の効用を $U_{B}$ と置くと、選択肢 A を選択する確率は下記のように表すことができます(Train 2009, p. 39):
$$
P(A) = \frac{1}{1 + exp(U_{B} - U_{A})}
$$
従って、「外交」のように本当にコーパスで利用された単語とランダムに選ばれた単語(ネガティブサンプル)の一対一の選択問題において、「外交」が選ばれる確率は:
$$
P(外交|c) = \frac{1}{1 + exp(\bar{U_{ネガティブサンプル_c}} - \bar{U_{外交_c})}}
$$
$$
P(外交|c) = \frac{1}{1 + exp(\alpha_{ネガティブサンプル} + \sum_{d=1}^{\infty} \left( \beta_{ネガティブサンプル,d} \cdot \delta_{d} \cdot \sum_{i \in c} \gamma_{i,d} \right) - \alpha_{外交} - \sum_{d=1}^{\infty} \left( \beta_{外交,d} \cdot \delta_{d} \cdot \sum_{i \in c} \gamma_{i,d} \right) }
$$
$$
P(外交|c) = \frac{1}{1 + exp(\alpha_{ネガティブサンプル} - \alpha_{外交} + \sum_{d=1}^{\infty} \left( (\beta_{ネガティブサンプル,d} - \beta_{外交, d}) \cdot \delta_{d} \cdot \sum_{i \in c} \gamma_{i,d}\right))}
$$
このように表すことができます。
この尤度を利用すれば、元々の word2vec におけるネガティブサンプルでは、正解(ここでいう「外交」)とネガティブサンプル(ここでいう「チーズ」など)の尤度を別々に評価する必要がありました。しかし、これを離散選択問題として定式化することで、一度の尤度関数の評価で済むため、計算すべきサンプルサイズが半減します。これにより、計算時間の短縮も期待できます。
事前分布
さて、ここからはパラメータの事前分布の設定について説明します。内容的にはほとんど
と被ってしまいますが、念の為本記事に転記します。
次元数の自動推定
まず、次元の重要度を決定するための棒折り過程のハイパーパラメータ$\gamma$を以下のようにサンプリングします:
$$
\omega \sim Gamma(0.001, 0.001)
$$
続いて、棒折り過程過程により、次元ごとの重要度$\omega_{d}$を構築します:
$$
\kappa_{d} \sim Beta(1, \omega)
$$
$$
\delta_{d} = \kappa_{d} \prod\limits_{l=1}^{d - 1} (1 - \kappa_{l})
$$
この処理を$d = 1$から$d = \infty$まで繰り返します。
ここでサンプリングされる単語分散表現ベクトルは無限次元を持ちますが、実際には多くの次元に対して$\omega_d$が0に近い値となるため、モデルが本質的に利用する次元数を自動的に推定することが可能となります。
単語分散表現
単語分散表現の生成において、分布の事前構造としてディリクレ過程を用います。まず、棒折り過程に必要なハイパーパラメータ$\alpha$を以下のようにサンプリングします:
$$
\phi \sim Gamma(0.001, 0.001)
$$
次に、クラスタ$p$に対して棒折り過程を適用し、クラスタ分布$p_{p}$を構築します:
$$
\pi_{p} \sim Beta(1, \phi)
$$
$$
p_{p} = \pi_{p} \prod\limits_{l=1}^{p - 1} (1 - \pi_{l})
$$
各クラスタ $p$ の中心ベクトル(無限次元)およびばらつきは次のようにサンプリングされます:
$$
P_{latent,p} \sim Normal(0, 1)
$$
$$
P_{\sigma,p} \sim Gamma(0.001, 0.001)
$$
単語$S$の分散表現ベクトル$\beta_S$は、まずカテゴリ分布により所属クラスタ$\eta_S$を以下のようにサンプリングし、
$$
\eta_{S} \sim Categorical(p)
$$
続いて、そのクラスタに基づく分布から以下のように生成されます:
$$
\beta_{S} \sim Normal(P_{latent, \eta_{S}}, P_{\sigma, \eta_{S}})
$$
これにより、単語$S$の分散表現ベクトルは無限次元かつクラスタ構造を持つ表現として得られます。
この一連の分散表現ベクトルを生成する分布のことをGといって、実証分析のところでその事後分布を可視化します。
Stan コード
Stan 言語によるモデル実装コードはこちらです:
functions {
vector stick_breaking(vector breaks){
int length = size(breaks) + 1;
vector[length] result;
result[1] = breaks[1];
real summed = result[1];
for (d in 2:(length - 1)) {
result[d] = (1 - summed) * breaks[d];
summed += result[d];
}
result[length] = 1 - summed;
return result;
}
real partial_sum_lpmf(
array[] int word,
int start, int end,
array[] int neg_word,
array[] int word_lag_1, array[] int word_lead_1,
array[] int word_lag_2, array[] int word_lead_2,
array[] int word_lag_3, array[] int word_lead_3,
vector word_intercept,
vector dimension,
array[] vector word_embedding,
array[] vector word_context
){
vector[end - start + 1] log_likelihood;
int count = 1;
for (i in start:end){
log_likelihood[count] = - log1p(
exp(
word_intercept[neg_word[i]] - word_intercept[word[count]] +
(dimension .* (
word_context[word_lag_1[i]] + word_context[word_lead_1[i]] +
word_context[word_lag_2[i]] + word_context[word_lead_2[i]] +
word_context[word_lag_3[i]] + word_context[word_lead_3[i]]
)) '* (word_embedding[neg_word[i]] - word_embedding[word[count]])
)
);
count += 1;
}
return(sum(log_likelihood));
}
}
data {
int dimension_type;
int group_type;
int word_type;
int N;
array[N] int word;
array[N] int neg_word;
array[N] int word_lag_1;
array[N] int word_lead_1;
array[N] int word_lag_2;
array[N] int word_lead_2;
array[N] int word_lag_3;
array[N] int word_lead_3;
}
parameters {
real<lower=0> dimension_alpha;
vector<lower=0, upper=1>[dimension_type - 1] dimension_breaks;
real<lower=0> group_alpha;
vector<lower=0, upper=1>[group_type - 1] group_breaks;
vector<lower=0>[group_type] group_sigma;
array[group_type] vector[dimension_type] group_word_embedding;
vector[word_type] word_intercept_unnormalized;
array[word_type] vector[dimension_type] word_embedding;
array[word_type] vector[dimension_type] word_context;
}
transformed parameters {
simplex[dimension_type] dimension;
simplex[group_type] group;
vector[word_type] word_intercept;
dimension = stick_breaking(dimension_breaks);
group = stick_breaking(group_breaks);
word_intercept = word_intercept_unnormalized - mean(word_intercept_unnormalized);
}
model {
dimension_alpha ~ gamma(0.001, 0.001);
dimension_breaks ~ beta(1, dimension_alpha);
group_alpha ~ gamma(0.001, 0.001);
group_breaks ~ beta(1, group_alpha);
group_sigma ~ gamma(0.001, 0.001);
for (i in 1:group_type){
group_word_embedding[i] ~ normal(0, 1);
}
word_intercept ~ normal(0, 10);
for (i in 1:word_type){
word_context[i] ~ normal(0, 1);
vector[group_type] case_when;
for (j in 1:group_type){
case_when[j] = log(group[j]) + normal_lpdf(word_embedding[i] | group_word_embedding[j], group_sigma[j]);
}
target += log_sum_exp(case_when);
}
int grainsize = 1;
target += reduce_sum(
partial_sum_lupmf, word,
grainsize,
neg_word,
word_lag_1, word_lead_1,
word_lag_2, word_lead_2,
word_lag_3, word_lead_3,
word_intercept,
dimension,
word_embedding,
word_context
);
}
generated quantities {
array[dimension_type] real G;
array[word_type] vector[dimension_type] weighted_word_embedding;
{
int sampled_group = categorical_rng(group);
G = normal_rng(group_word_embedding[sampled_group], group_sigma[sampled_group]);
for (i in 1:dimension_type){
G[i] = G[i] * dimension[i];
}
}
{
for (i in 1:word_type){
for (j in 1:dimension_type){
weighted_word_embedding[i, j] = word_embedding[i, j] * dimension[j];
}
}
}
}
前処理とモデル推定
話がすごく長くなりましたね、ここからは実装のための前処理に入ります!
今回の分析では、livedoorニュースコーパスを利用します。
まず、テキストデータの読み込みとMecabで単語分割等を実施します:
mecabbing <- function(text){
this_review <- stringr::str_replace_all(text, "[^一-龠ぁ-んーァ-ヶー]", " ")
mecab_output <- unlist(RMeCab::RMeCabC(this_review, 1))
mecab_combined <- stringr::str_c(mecab_output[which(names(mecab_output) == "名詞")], collapse = " ")
return(mecab_combined)
}
`%>%` <- magrittr::`%>%`
future::plan(future::multisession)
review_df <- list.files("text") %>%
.[which(stringr::str_detect(., ".txt") == FALSE)] |>
furrr::future_map(
\(this_file){
this_file %>%
stringr::str_c("text/", .) |>
list.files() %>%
.[which(stringr::str_detect(., "LICENSE") == FALSE)] %>%
stringr::str_c("text/", this_file, "/", .) |>
purrr::map(
\(this_text){
this_text |>
readr::read_lines() |>
stringr::str_c(collapse = " ") |>
mecabbing() |>
stringr::str_remove_all(
quanteda::stopwords("ja", source = "marimo") |>
c("的", "の", "こと", "さ", "ら", "今", "いま") |>
stringr::str_c(collapse = "|")
) |>
tibble::tibble(
category = this_file,
text = _
)
}
)
},
.progress = TRUE
) |>
dplyr::bind_rows() |>
dplyr::mutate(
doc_id = dplyr::row_number()
)
次に、合計で100回以上出現した単語だけをまとめて、単語マスターを作成します:
word_use <- review_df |>
dplyr::pull(text) |>
quanteda::phrase() |>
quanteda::tokens() |>
quanteda::dfm() |>
quanteda::dfm_trim(min_docfreq = 100) |>
colnames()
word_master <- word_use |>
tibble::tibble(
word = _
) |>
dplyr::arrange(word) |>
dplyr::mutate(
word_id = dplyr::row_number()
)
次に、かなりものすごく長いパイプで
- データフレイムを単語で縦持ちにする
- 不要な単語の削除
- 文脈(前後3単語、計6単語)を抽出
- ネガティブサンプルを初回抽出
- もしネガティブサンプルが本当の単語と被ってしまったら、再抽出する
を実施します。ここで特に説明したいのは、!!"カラム名" := 定義 の文法と、purrr::map(または purrr::map2 など)をパイプ内で使う方法です。
-
!!"カラム名" := 定義は、文字列で指定したカラム名を新しい列として作ることができる tidy evaluation の書き方です。例えば、変数col_name <- "negative_sample"を指定して、下記のように書くと、新しい列 "negative_sample" が作成されます:
> col_name <- "negative_sample"
> tibble::tibble(a = 1) |> dplyr::mutate(!!col_name := 12)
# A tibble: 1 × 2
a negative_sample
<dbl> <dbl>
1 1 12
-
purrr::doneは、purrr::reduceの早期終了のための特殊な関数です。具体的にいうと、reduce()がリストやベクトルの要素を順番に畳み込む処理を行う際、途中で条件を満たした場合に計算を打ち切り、残りの要素を無視して結果を返すことができます。
例えば、ある処理を順に適用していき、ある条件が満たされた時点で計算を終了したい場合に purrr::done() を返すことで、reduce() は残りの要素を評価せずに即座に終了します。
> purrr::reduce(1:10, \(x, i) {
if (i > 5) {
purrr::done(x) # iが5を超えたら早期終了
} else {
x + i
}
})
[1] 15
さて、この二つのtidyverse系パッケージの機能を活用して、前処理を終わらせます:
set.seed(12345)
review_df_long <- review_df |>
dplyr::mutate(
word = text |>
quanteda::phrase() |>
quanteda::tokens() |>
quanteda::tokens_remove("の") |>
as.list()
) |>
tidyr::unnest_longer(word) |>
dplyr::filter(word %in% word_master$word) |>
dplyr::select(doc_id, word, category) |>
dplyr::left_join(word_master, by = "word") |>
dplyr::group_by(doc_id) |>
purrr::reduce(
1:3,
\(this_df, i){
this_df |>
dplyr::mutate(
!!stringr::str_c("lag_", i) := dplyr::lag(word_id, i),
!!stringr::str_c("lead_", i) := dplyr::lead(word_id, i),
)
},
.init = _
) |>
dplyr::ungroup() |>
tidyr::drop_na() |>
dplyr::mutate(
neg_word_id = sample(word_master$word_id, dplyr::n(), replace = TRUE)
) |>
purrr::reduce(
1:1000, # 流石に1000回繰り返してもたまたま被るやつがあるとは思えない
\(this_df, i){
if (sum(this_df$word_id == this_df$neg_word_id) == 0){
return(purrr::done(this_df))
} else {
done_df <- this_df |>
dplyr::filter(word_id != neg_word_id)
not_done_df <- this_df |>
dplyr::filter(word_id == neg_word_id) |>
dplyr::mutate(
neg_word_id = sample(word_master$word_id, dplyr::n(), replace = TRUE)
)
return(dplyr::bind_rows(done_df, not_done_df))
}
},
.init = _
)
次に、モデルをコンパイルして:
m_init <- cmdstanr::cmdstan_model("discrete_choice_word2vec.stan",
cpp_options = list(
stan_threads = TRUE
)
)
変分推論を実施します:
> m_estimate <- m_init$variational(
threads = 6,
seed = 1234,
data = list(
dimension_type = 15,
group_type = 10,
word_type = nrow(word_master),
N = nrow(review_df_long),
word = review_df_long$word_id,
neg_word = review_df_long$neg_word_id,
word_lag_1 = review_df_long$lag_1,
word_lead_1 = review_df_long$lead_1,
word_lag_2 = review_df_long$lag_2,
word_lead_2 = review_df_long$lead_2,
word_lag_3 = review_df_long$lag_3,
word_lead_3 = review_df_long$lead_3
)
)
------------------------------------------------------------
EXPERIMENTAL ALGORITHM:
This procedure has not been thoroughly tested and may be unstable
or buggy. The interface is subject to change.
------------------------------------------------------------
Gradient evaluation took 0.689116 seconds
1000 transitions using 10 leapfrog steps per transition would take 6891.16 seconds.
Adjust your expectations accordingly!
Begin eta adaptation.
Iteration: 1 / 250 [ 0%] (Adaptation)
Iteration: 50 / 250 [ 20%] (Adaptation)
Iteration: 100 / 250 [ 40%] (Adaptation)
Iteration: 150 / 250 [ 60%] (Adaptation)
Iteration: 200 / 250 [ 80%] (Adaptation)
Success! Found best value [eta = 1] earlier than expected.
Begin stochastic gradient ascent.
iter ELBO delta_ELBO_mean delta_ELBO_med notes
100 -346268.226 1.000 1.000
200 -310176.536 0.558 1.000
300 -297892.589 0.386 0.116
400 -295094.884 0.292 0.116
500 -294421.526 0.234 0.041
600 -294168.948 0.195 0.041
700 -293907.744 0.167 0.009 MEDIAN ELBO CONVERGED
Drawing a sample of size 1000 from the approximate posterior...
COMPLETED.
Finished in 651.1 seconds.
約 10 分で終わりました!
結果をデータフレイムで保存します:
m_summary <- m_estimate$summary()
結果の可視化
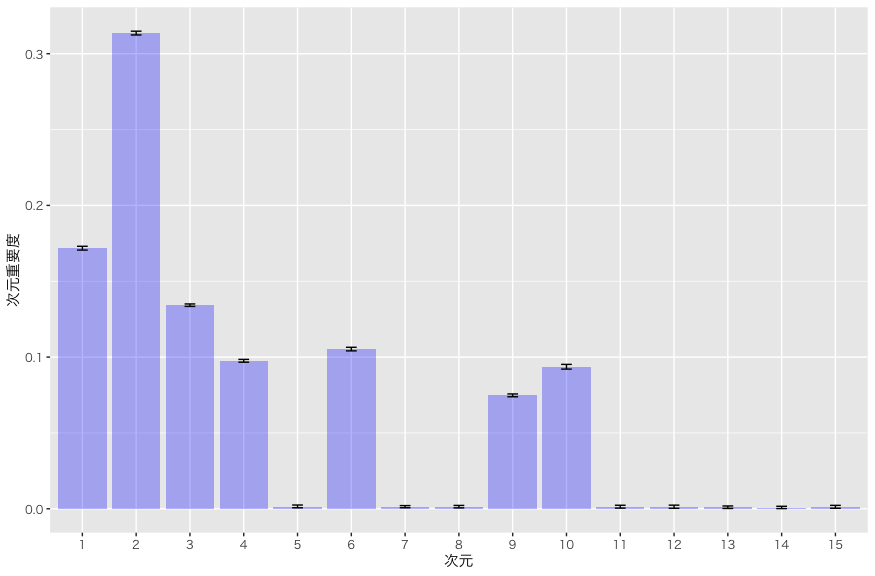
まずは、推定された次元数から確認しましょう:
m_summary |>
dplyr::filter(stringr::str_detect(variable, "^dimension\\[")) |>
ggplot2::ggplot() +
ggplot2::geom_bar(ggplot2::aes(x = as.factor(1:15), y = mean),
stat = "identity", fill = ggplot2::alpha("blue", 0.3)) +
ggplot2::geom_errorbar(
ggplot2::aes(x = as.factor(1:15), ymin = q5, ymax = q95),
width = 0.2
) +
ggplot2::labs(
x = "次元",
y = "次元重要度"
) +
ggplot2::theme_gray(base_family = "HiraKakuPro-W3")
実際は 7 次元くらいが利用されています。まだ明確な理論的言語化には至っていませんが、本モデルのように「各次元に異なる重みを与える」構造ではなく、一般的なword2vec、あるいはTransformerのように「すべての次元が等しく重要である」と仮定する場合、たとえば本モデルで推定された重みが0.5および0.25の次元を同じように表現するには、それぞれを2つおよび1つの等重みの次元に分割して表現する必要があります。
言い換えれば、次元ごとの重要度を柔軟に調整できる構造を採用することで、同じ表現力を保ちながら、必要な次元数を大幅に削減できる可能性があるということです。
あくまでも現時点では仮説に過ぎませんが、大規模言語モデルは、実際には同じ情報を異なる次元で大量に・重複的に保持しているだけなのではないか、という可能性も示唆されます。
次に、単語の分散表現とその分布Gをt-SNEで可視化します:
set.seed(12345)
tsne_df <- m_summary |>
dplyr::filter(stringr::str_detect(variable, "weighted_word_embedding\\[")) |>
dplyr::pull(mean) |>
matrix(ncol = 15) |>
rbind(
m_estimate$draws("G") |>
as.data.frame() |>
as.matrix()
) |>
Rtsne::Rtsne() |>
purrr::pluck("Y") |>
as.data.frame() |>
tibble::tibble() |>
dplyr::bind_cols(
type = c(rep("word", nrow(word_master)), rep("group", 1000)),
word = c(word_master$word, rep("group", 1000))
)
g_tsne <- tsne_df |>
dplyr::filter(type == "word") |>
ggplot2::ggplot() +
ggplot2::geom_text(ggplot2::aes(x = V1, y = V2, label = word), color = ggplot2::alpha("blue", 0.3)) +
ggplot2::geom_density_2d(data = tsne_df |>
dplyr::filter(type == "group"),
ggplot2::aes(x = V1, y = V2),
color = ggplot2::alpha("black", 0.2),
show.legend = FALSE
) +
ggplot2::theme_gray(base_family = "HiraKakuPro-W3") +
ggplot2::xlim(c(-50, 50)) +
ggplot2::ylim(c(-50, 50))
plotly::ggplotly(g_tsne)
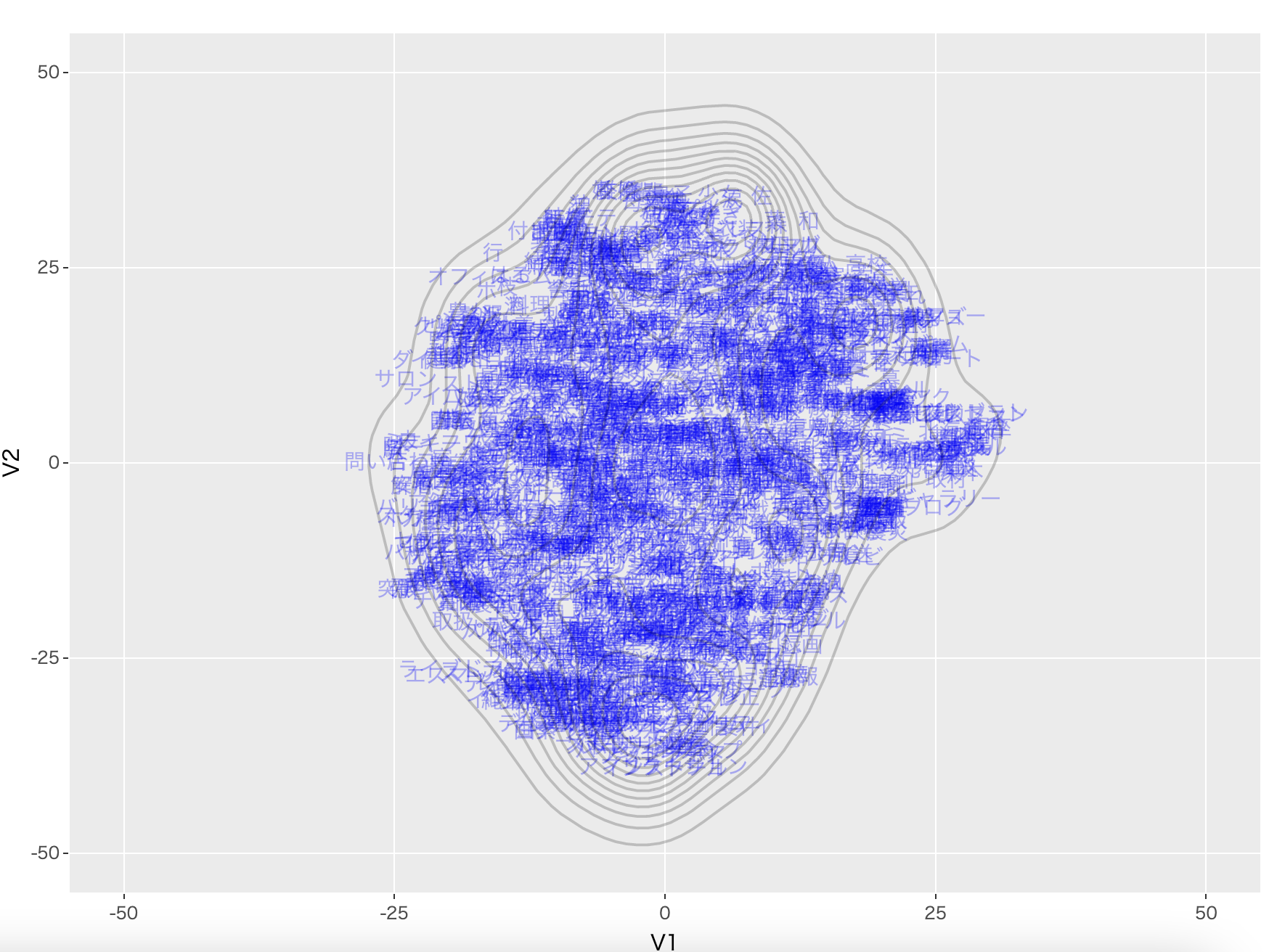
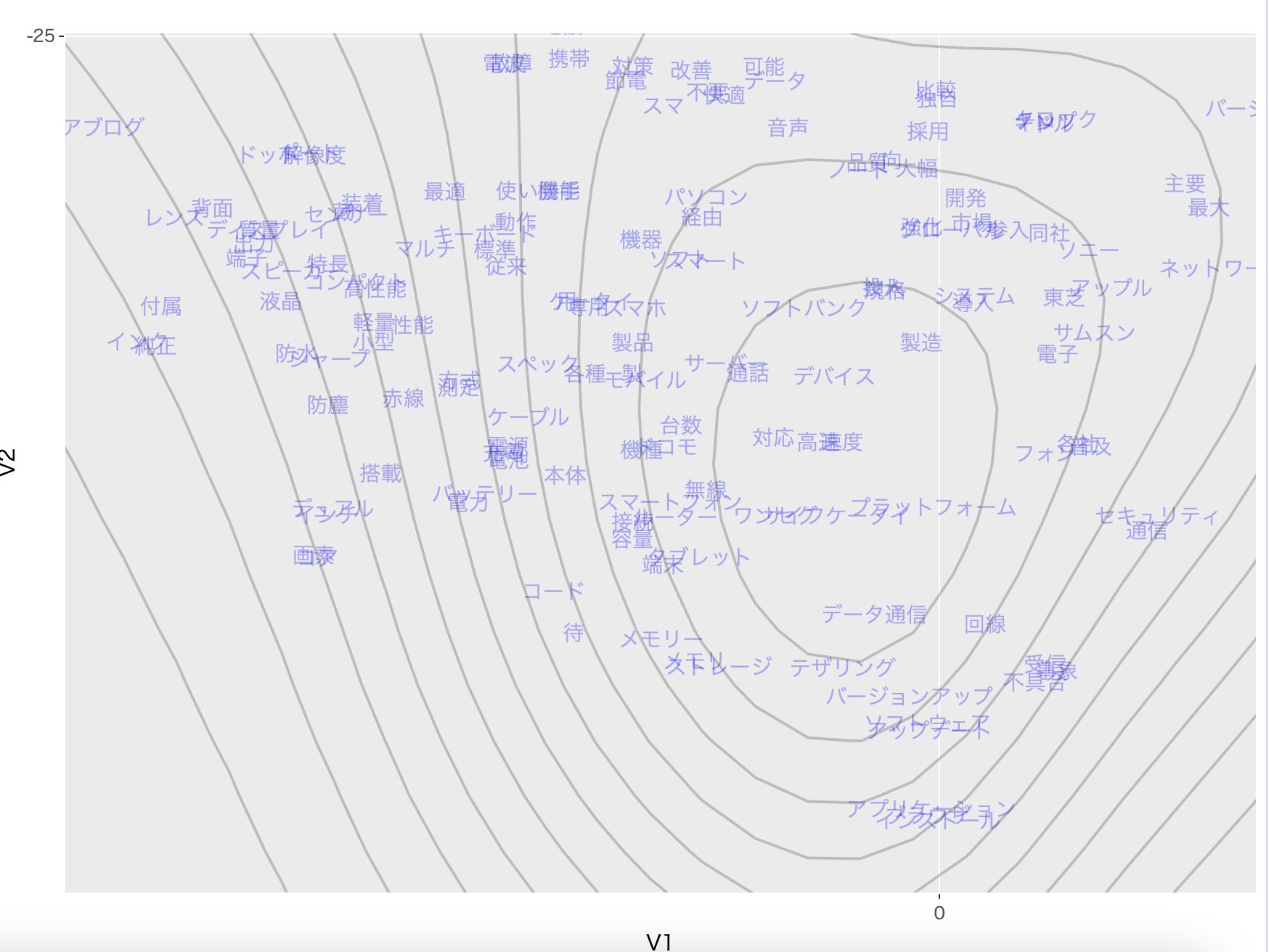
文字が単語の分散表現に対して $\delta$ によって重み付けされたベクトルを、t-SNEによって2次元に投影した際の位置を示しています。図中の等高線は、分散表現の分布Gの事後分布を可視化したものです。
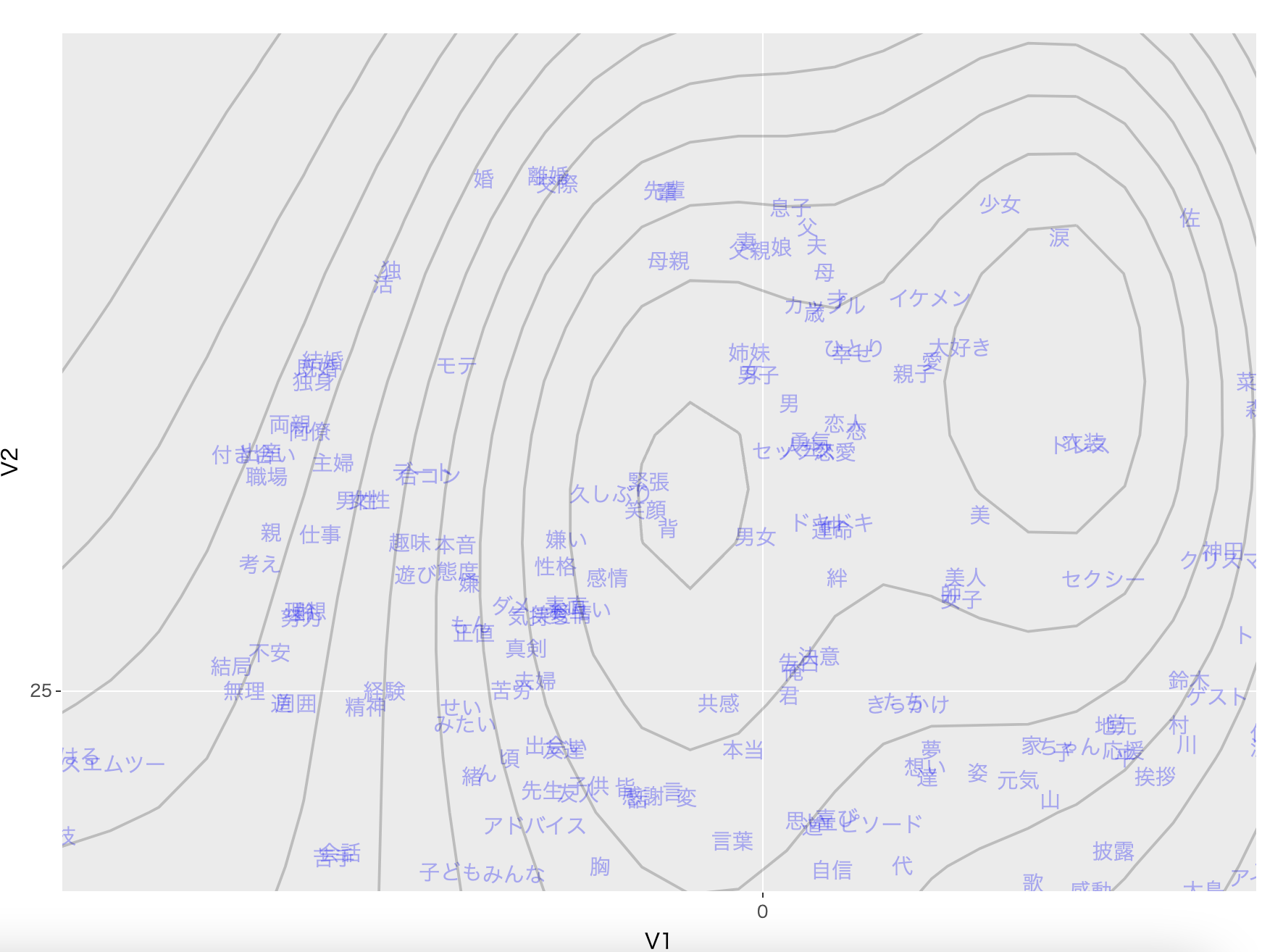
まず上の方を確認すると:
「親子」「父」「夫」「母」などの家族を表す単語が近くにあり、かつ「結婚」「既婚」「独身」がほぼ重なっていることから、この話者の選択問題をミクロ経済学とミクロ計量経済学だけで尤度関数を定式化した word2vec に似たモデルも、日本語の意味構造を問題なく捉えられていると評価できます。
他にも:
一番右の「銀座」、「渋谷」、「東京」が近くにあるのも、日本語の構造を捉えられた証拠です。
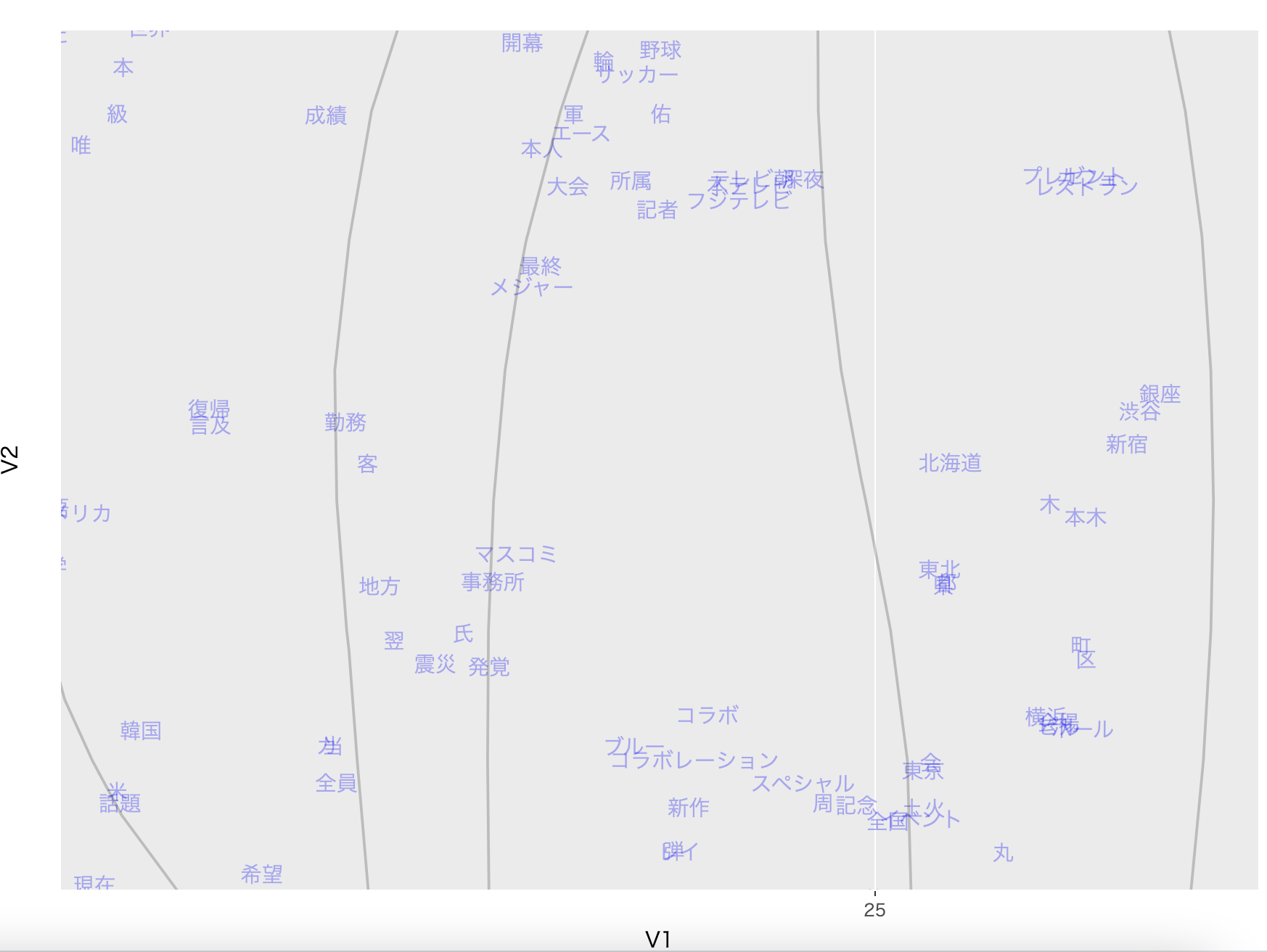
最後に、下の方に行くと:
ほぼ全てが IT、家電系の単語になっているのを確認できます。
結論
いかがでしたか?
本記事では、ミクロ経済学の効用最大化理論と離散選択理論を利用することで、word2vec におけるネガティブサンプリングという経験的な手法に対し、強固な理論的基盤を与え、さらに計算効率の向上を実現する新たなモデルを提案しました。
従来のモデルは、ネガティブサンプルを単なる「誤ったペア」として扱うことが多かったのに対し、本モデルはこれを「話者が文脈に応じて選択しなかった単語」という効用最大化アクターの行動として再解釈しました。このアプローチにより、正解データとネガティブサンプルデータを同一レコードとして統合でき、尤度関数の評価回数を半減させることで、計算資源を効率的に利用する道を開きました。
また、モデルの性能について、livedoorニュースコーパスに適用した結果、以下の2つの重要な示唆が得られました。
- 意味構造の正確な学習: 「父」や「母」といった家族を表す単語群や、「銀座」「渋谷」「東京」といった地名が近接して配置されるなど、人間が認識する意味構造を正確に捉えていることが確認できました。これは、経済学的なフレームワークが自然言語の意味論を捉える上で有効であることを示しています。
- 次元数の自動推定: ディリクレ過程と棒折り過程を用いた階層ベイズモデルにより、モデルが本質的に必要とする次元数を自動的に推定できることが示されました。この柔軟な構造は、従来の固定次元のモデルでは見落とされがちだった、言語構造の階層的な特徴を捉える可能性を秘めています。また、これは大規模言語モデルが持つ冗長な次元構造を削減し、より効率的な表現を可能にするという仮説を支持するものです。
本記事で紹介したモデルは、経済学と機械学習という二つの分野を融合させることで、理論的な厳密性と実用的な効率性の両方を追求する試みです。得られた結果は、この融合が単なる「数学遊び」ではなく、言語モデルの設計に新たな視点をもたらし、より洗練された表現学習へと繋がる可能性を示しています。
今後は、このフレームワークをより大規模なコーパスに適用し、そのスケーラビリティを検証するとともに、経済学分野で開発されたプロビットモデルや入れ子型ロジットモデルといったさらに高度な離散選択モデルを応用することで、IIAの仮定から脱却した、より現実に近い言語行動をモデリングすることを目指します。
最後に、私たちと一緒に働きたい方はぜひ下記のリンクもご確認ください:
参考文献
Train, Kenneth E. Discrete choice methods with simulation. Cambridge university press, 2009.
Varian, Hal R. Microeconomic analysis. Vol. 3. New York: Norton, 1992.