はじめに
こんにちは、事業会社で働いているデータサイエンティストです。
本記事では、Conley, Hansen, McCulloch, and Rossi(2008)、Li and Ansari(2014)、Yang and Dunson(2010)を参考に、ベイズ機械学習の一手法であるディリクレ過程混合モデルを用いて、操作変数推定を行うモデルを紹介します。
問題意識
操作変数法(Instrumental Variables: IV)は、次のような状況で役立ちます。
$$
Y = X\beta + \epsilon_{1}
$$
$$
X = Z\gamma + \epsilon_{2}
$$
ここで、$\epsilon_{1}$と$\epsilon_{2}$が相関していると、$X$と$Y$の間に因果関係ではない相関(交絡)が生じてしまい、$\beta$ を正しく推定できません。操作変数 $Z$ を用いることで、この交絡を解消しようというのが IV の考え方です。
これをより直感的な実例で説明しましょう。
たとえば、あるアプリゲームのプロダクトマネージャが次のように考えたとします。
「ゲームへの課金が増えると、ユーザーの継続率も上がるのではないか?」
この関係を調べるために、次のような回帰式を考えます:
$$
\text{ゲーム継続率} = \text{ゲーム課金} \cdot \beta + \epsilon_{1}
$$
しかし、ここで問題があります。課金をたくさんするユーザーは、そもそもゲームが大好きなヘビーユーザーである可能性が高く、課金とは無関係に継続率が高いかもしれません。つまり、$\epsilon_1$と課金量に関係する$\epsilon_2$が相関している可能性があります。
そこで、プロダクトマネージャは「ゲーム課金クーポン」を操作変数として使うことを考えます:
$$
\text{ゲーム課金} = \text{ゲーム課金クーポン} \cdot \gamma + \epsilon_2
$$
この「クーポン」はユーザーの性格とは無関係に配布されている(と仮定)ため、ゲーム継続率に直接影響を与えず、ゲーム課金だけに影響を与える良い操作変数になる可能性があります。
このようにして、操作変数法を使えば、単なる相関ではなく、因果関係としての$\beta$を推定することができます。
頻度論操作変数法
ここからは、統計学・計量経済学の話に入ります。伝統的な計量経済学では、操作変数推定量(IV推定量)は以下のような直交条件によって定義されます:
$$
\mathbb{E}(Z\epsilon_{1}) = 0
$$
これは、前述の例で説明したように、クーポン(操作変数)がユーザーの性格や嗜好($\epsilon_1$)とは無関係に配布されている、つまり$Z$と$\epsilon_1$が相関していないことを意味します。この仮定を用いて、操作変数推定量$\beta_{IV}$を次のように導出します:
$$
\mathbb{E}(Z(Y - X\beta_{IV})) = 0
$$
$$
\mathbb{E}(ZY - ZX\beta_{IV}) = 0
$$
$$
\mathbb{E}(ZY) - \mathbb{E}(ZX)\beta_{IV} = 0
$$
$$
\mathbb{E}(ZY) = \mathbb{E}(ZX)\beta_{IV}
$$
$$
\beta_{IV} = (\mathbb{E}(ZX))^{-1}\mathbb{E}(ZY)
$$
重要なのは、$\epsilon_1$や$\epsilon_2$の分布の具体的な形状には依存せず、操作変数と誤差項が無相関であるという一つの仮定だけに基づいて推定が行われているという点です。
これに対して、本記事で紹介するモデルでは、ディリクレ過程混合モデルを用いて、$\epsilon_1$と$\epsilon_2$の分布自体を柔軟に学習しながら、$\beta$を推定します。
このアプローチは、誤差項の構造が複雑だったり、非正規的であっても、それをモデリングの一部として取り込むことで、よりロバストかつ柔軟な因果推定を可能にします。
ディリクレ過程混合操作変数法
ディリクレ過程混合操作変数法の基本的な発想は、少々乱暴に言えば、無限個の正規分布のペアを用いて、誤差項$\epsilon_1$と$\epsilon_2$の分布を近似するというものです。
まず、ディリクレ過程の集中度を表すハイパーパラメータ$\alpha$を次のようにガンマ分布からサンプリングします:
$$
\alpha \sim Gamma(0.001, 0.001)
$$
次に、棒折り過程を用いて、各ペア$p$に属する確率$p_p$を構築します。これは、クラスタ数が理論上無限大であるという前提に基づいており、以下のように定義されます:
$$
\pi_p \sim Beta(1, \alpha)
$$
$$
p_p = \pi_p \prod_{l=1}^{p - 1} (1 - \pi_l)
$$
この$p_p$は、観測値がクラスタ$p$に属する事前確率を表しています。言い換えれば、全ての観測値のうち$p_p$の割合のデータが、クラスタ$p$に対応する2つの独立した正規分布から$\epsilon_1$ と$\epsilon_2$を生成されたと考えます。
次に、各観測値$i$について、どのクラスタ(ペア)に属するかを次のようにサンプリングします:
$$
\eta_i \sim Categorical(p)
$$
最後に、クラスタ$\eta_{i}$に応じて、それぞれの誤差項は次のようにサンプリングされます:
$$
\epsilon_{1,i} \sim Normal(\mu_{1,\eta_i}, \sigma_{1,\eta_i})
$$
$$
\epsilon_{2,i} \sim Normal(\mu_{2,\eta_i}, \sigma_{2,\eta_i})
$$
このようにして、誤差項$\epsilon_1$と$\epsilon_2$が独立した二つの正規分布からサンプリングされていますが、実は両者の複雑な依存構造を、柔軟にかつ非パラメトリックに捉えることが可能となります。結果として、従来の操作変数法よりも誤差項の非正規性にロバストかつ表現力の高い因果推定が実現されます。
Stan言語での実装はこのようになります。実装では、$\epsilon_{1}$と$\epsilon_{2}$の平均がゼロになるように、$\mu_{1}$と$\mu_{2}$を標準化しています。
functions {
vector stick_breaking(vector breaks){
int length = size(breaks) + 1;
vector[length] result;
result[1] = breaks[1];
real summed = result[1];
for (d in 2:(length - 1)) {
result[d] = (1 - summed) * breaks[d];
summed += result[d];
}
result[length] = 1 - summed;
return result;
}
}
data {
int group_type;
int N;
vector[N] z;
vector[N] x;
vector[N] y;
}
parameters {
real<lower=0> group_alpha; // ディリクレ過程の全体のパラメータ
vector<lower=0, upper=1>[group_type - 1] group_breaks; // ディリクレ過程のstick-breaking representationのためのパラメータ
matrix[group_type, 2] error_mu_unnormalized;
matrix<lower=0>[group_type, 2] error_sigma;
vector[2] intercept;
vector[2] beta;
}
transformed parameters {
simplex[group_type] group;
matrix[group_type, 2] error_mu;
group = stick_breaking(group_breaks);
error_mu[:,1] = error_mu_unnormalized[:,1] - error_mu_unnormalized[:,1] '* group;
error_mu[:,2] = error_mu_unnormalized[:,2] - error_mu_unnormalized[:,2] '* group;
}
model {
group_alpha ~ gamma(0.001, 0.001);
group_breaks ~ beta(1, group_alpha);
to_vector(error_mu) ~ normal(0, 10);
to_vector(error_sigma) ~ inv_gamma(5, 5);
intercept ~ normal(0, 10);
beta ~ normal(0, 10);
for (i in 1:N){
vector[group_type] case_when;
for (g in 1:group_type){
case_when[g] = log(group[g]) +
normal_lpdf(x[i] | intercept[1] + beta[1] * z[i] + error_mu[g, 1], error_sigma[g, 1]) +
normal_lpdf(y[i] | intercept[2] + beta[2] * x[i] + error_mu[g, 2], error_sigma[g, 2]);
}
target += log_sum_exp(case_when);
}
}
generated quantities {
vector[2] error_sample;
{
int eta = categorical_rng(group);
error_sample[1] = normal_rng(error_mu[eta, 1], error_sigma[eta, 1]);
error_sample[2] = normal_rng(error_mu[eta, 2], error_sigma[eta, 2]);
}
}
データシミュレーションとモデル推定
ここでは
$$
y = -0.5 \cdot x + \epsilon_{2}
$$
$$
x = 0.9 \cdot z + \epsilon_{1}
$$
$$
\begin{bmatrix}
\epsilon_1 \
\epsilon_2
\end{bmatrix}'
\sim Normal \left(
\begin{bmatrix}
0 \
0
\end{bmatrix}',
\begin{bmatrix}
1 & 0.8 \\
0.8 & 1
\end{bmatrix}
\right)
$$
の状況でデータを10000件生成します:
set.seed(123456)
df <- 10000 |>
mvtnorm::rmvnorm(c(0, 0), sigma = matrix(c(1, 0.8, 0.8, 1), nrow = 2)) |>
tibble::tibble(
e = _
) |>
dplyr::mutate(
e_1 = e[,1],
e_2 = e[,2],
z = rnorm(dplyr::n()),
x = 0.9 * z + e_1,
y = - 0.5 * x + e_2
)
続いて、Stanモデルのコンパイルと推定を実施します:
m_init <- cmdstanr::cmdstan_model("bayes_iv.stan")
> m_estimate <- m_init$variational(
data = list(
group_type = 10,
N = nrow(df),
z = df$z,
x = df$x,
y = df$y
),
draws = nrow(df)
)
------------------------------------------------------------
EXPERIMENTAL ALGORITHM:
This procedure has not been thoroughly tested and may be unstable
or buggy. The interface is subject to change.
------------------------------------------------------------
Gradient evaluation took 0.023994 seconds
1000 transitions using 10 leapfrog steps per transition would take 239.94 seconds.
Adjust your expectations accordingly!
Begin eta adaptation.
Iteration: 1 / 250 [ 0%] (Adaptation)
Iteration: 50 / 250 [ 20%] (Adaptation)
Iteration: 100 / 250 [ 40%] (Adaptation)
Iteration: 150 / 250 [ 60%] (Adaptation)
Iteration: 200 / 250 [ 80%] (Adaptation)
Success! Found best value [eta = 1] earlier than expected.
Begin stochastic gradient ascent.
iter ELBO delta_ELBO_mean delta_ELBO_med notes
100 -24693.969 1.000 1.000
200 -23709.416 0.521 1.000
300 -23570.380 0.349 0.042
400 -23623.538 0.262 0.042
500 -23694.164 0.211 0.006 MEDIAN ELBO CONVERGED
Drawing a sample of size 10000 from the approximate posterior...
COMPLETED.
Finished in 50.8 seconds.
シミュレーションしたデータと同じ件数の事後分布を抽出させるので、少し時間がかかりました。
結果を保存します:
m_summary <- m_estimate$summary(
NULL,
"mean",
quantiles = ~ posterior::quantile2(., probs = c(0.025, 0.975))
)
推定結果確認
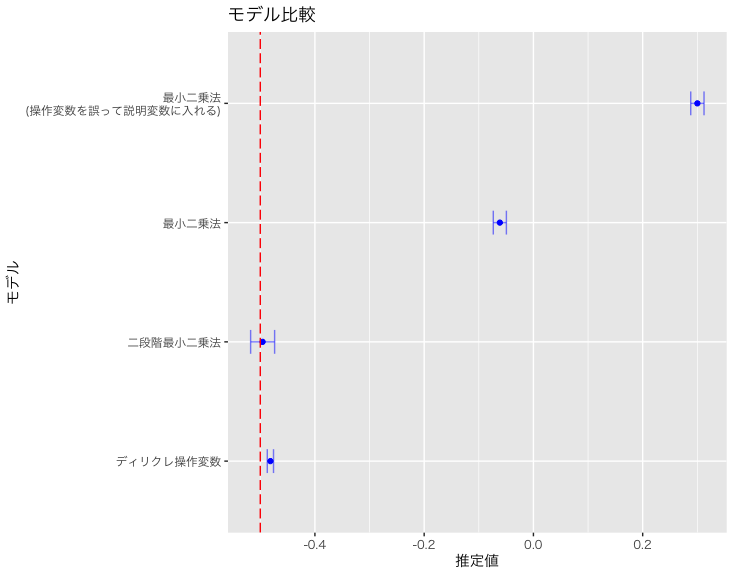
ここではまず、本モデルで推定された係数を確認します。比較のために、以下の3つのケースと並べて示します:
- 頻度論に基づく操作変数法(二段階最小二乗法)
- 内生性を無視した通常の最小二乗法(最小二乗法)
- 操作変数そのものを誤って説明変数に含めた最小二乗法
m_summary |>
dplyr::filter(stringr::str_detect(variable, "^beta\\[2")) |>
dplyr::mutate(
model = "ディリクレ操作変数"
) |>
dplyr::select(model, mean, q2.5, q97.5) |>
dplyr::bind_rows(
df |>
lm(y ~ x, data = _) |>
summary() |>
coef() |>
data.frame() |>
tibble::rownames_to_column(var = "var") |>
tibble::as_tibble() |>
dplyr::filter(var == "x") |>
dplyr::mutate(
mean = Estimate,
q2.5 = Estimate - 2 * `Std..Error`,
q97.5 = Estimate + 2 * `Std..Error`,
model = "最小二乗法"
) |>
dplyr::select(model, mean, q2.5, q97.5)
) |>
dplyr::bind_rows(
df |>
lm(y ~ x + z, data = _) |>
summary() |>
coef() |>
data.frame() |>
tibble::rownames_to_column(var = "var") |>
tibble::as_tibble() |>
dplyr::filter(var == "x") |>
dplyr::mutate(
mean = Estimate,
q2.5 = Estimate - 2 * `Std..Error`,
q97.5 = Estimate + 2 * `Std..Error`,
model = "最小二乗法\n(操作変数を誤って説明変数に入れる)"
) |>
dplyr::select(model, mean, q2.5, q97.5)
) |>
dplyr::bind_rows(
df |>
ivreg::ivreg(y ~ x | z, data = _) |>
summary() |>
coef() |>
data.frame() |>
tibble::rownames_to_column(var = "var") |>
tibble::as_tibble() |>
dplyr::filter(var == "x") |>
dplyr::mutate(
mean = Estimate,
q2.5 = Estimate - 2 * `Std..Error`,
q97.5 = Estimate + 2 * `Std..Error`,
model = "二段階最小二乗法"
) |>
dplyr::select(model, mean, q2.5, q97.5)
) |>
ggplot2::ggplot() +
ggplot2::geom_point(ggplot2::aes(x = mean, y = model), color = "blue") +
ggplot2::geom_errorbarh(ggplot2::aes(xmin = q2.5, xmax = q97.5, y = model), position = "dodge", height = 0.2, color = ggplot2::alpha("blue", 0.5)) +
ggplot2::geom_vline(xintercept = -0.5, linetype = "longdash", color = "red") +
ggplot2::labs(
title = "モデル比較",
x = "推定値",
y = "モデル"
) +
ggplot2::theme_gray(base_family = "HiraKakuPro-W3")
図の中の破線はパラメータの真の値である-0.5の位置を示しています。このように、頻度論に基づく二段階最小二乗法は、真の値に最も近い推定結果を示しており、本記事で実装したディリクレ過程混合操作変数モデルも、それに次ぐ精度で悪くないパフォーマンスを示しています。
一方で、内生性を無視した通常の最小二乗法は、推定値が大きく乖離しており、さらに操作変数を誤って説明変数に含めたモデルに至っては、推定値の符号すら逆転しており、完全に不適切な結果となっています。
操作変数を誤って説明変数として回帰式に含めてしまうと、なぜこのように不適切な結果につながるのかについては、別の記事であらためて詳しく解説します。
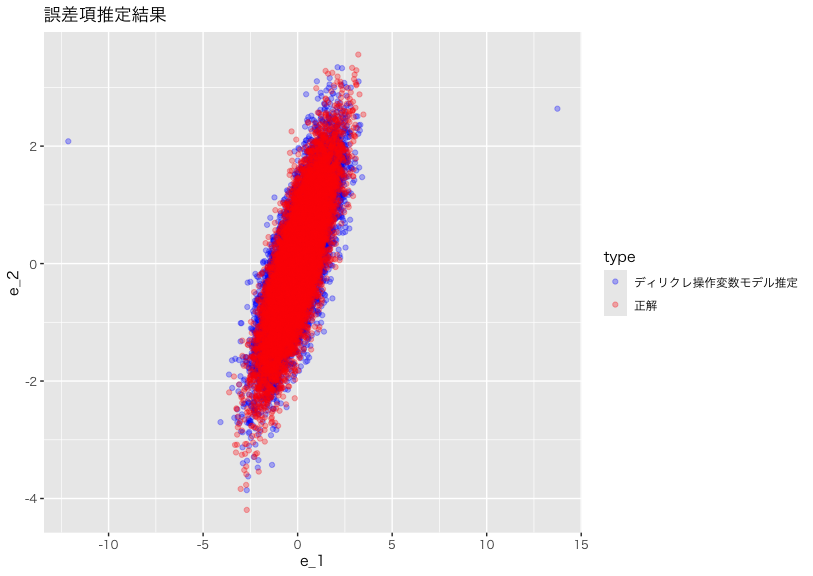
最後に、ディリクレ過程混合モデルが、$\epsilon_{1}$と$\epsilon_{2}$の分布を正しく捉えられるかを確認しましょう:
m_estimate$draws("error_sample") |>
tibble::as_tibble() |>
dplyr::mutate(
dplyr::across(
dplyr::everything(),
~ as.numeric(.)
)
) |>
`colnames<-`(c("e_1", "e_2")) |>
dplyr::mutate(
type = "ディリクレ操作変数モデル推定"
) |>
dplyr::bind_rows(
df |>
dplyr::mutate(
type = "正解"
) |>
dplyr::select(type, e_1, e_2)
) |>
ggplot2::ggplot() +
ggplot2::geom_point(ggplot2::aes(x = e_1, y = e_2, color = type), alpha = 0.3) +
ggplot2::scale_color_manual(values = c("ディリクレ操作変数モデル推定" = "blue",
"正解" = "red")) +
ggplot2::labs(
title = "誤差項推定結果"
) +
ggplot2::theme_gray(base_family = "HiraKakuPro-W3")
このように、一部の点が大きく外れているが、概ね分布の形を再現できているといえるのではないでしょうか。
結論
いかがでしょうか?本モデルを用いることで、頻度論的な手法では困難な、$\epsilon_{1}$と$\epsilon_{2}$の分布そのものを推定したり、他の階層ベイズ構造を保ったまま内生性の問題に対処したりすることが可能になります。
私たちと一緒にデータサイエンスの力を使って社会を改善していきたい方はぜひこちらのページをご確認ください:
参考文献
Conley, T. G., Hansen, C. B., McCulloch, R. E., & Rossi, P. E. (2008). A semi-parametric Bayesian approach to the instrumental variable problem. Journal of Econometrics, 144(1), 276-305.
Li, Y., & Ansari, A. (2014). A Bayesian semiparametric approach for endogeneity and heterogeneity in choice models. Management Science, 60(5), 1161-1179.
Yang, M., & Dunson, D. B. (2010). Bayesian semiparametric structural equation models with latent variables. Psychometrika, 75(4), 675-693.