はじめに
こんにちは、事業会社で働いているデータサイエンティストです。
本記事は、前回の記事の続編です:
実際にモーメント条件を利用して、モデルがきちんと正規分布の平均を推定できるかを確認します。
モデル説明
詳細の説明は前回の記事を参照していただきたいですが、簡単に振り返ると、一般化モーメント法は、観測値 $i$ に対して得られるモーメントベクトル $m_i(\theta)$ をまとめて、以下の目的関数を最小化する $\theta$ を推定します:
$$
\max_{\theta} \ L_n(\theta) = \ -0.5 \left( \frac{1}{\sqrt{n}} \sum_{i=1}^{n} m_i(\theta) \right)' W_n(\theta) \left( \frac{1}{\sqrt{n}} \sum_{i=1}^{n} m_i(\theta) \right)
$$
さらに、ベイズ版一般化モーメントの場合、一般化モーメント法の目的関数 $L_n(\theta)$ を次のように変形することで、擬似的な事後分布を定義します:
$$
p_n(\theta) = \frac{e^{L_n(\theta)} \pi(\theta)}{\int_{\Theta} e^{L_n(\theta)} \pi(\theta) d\theta}
$$
ここで、$\pi(\theta)$ は $\theta$ に対する事前分布を表します。
この $p_n(\theta)$ を、擬似事後分布とみなすことで、MCMCなどのベイズ的推定手法を適用可能になります。
なかなか面白い発想ですね。でも、これって本当に上手くいくんですか?というわけで、確認しましょう!
いきなり難しい話に入ってもあまり意味がないので、まず正規分布のモーメント条件でベイズ一般化モーメント法の性能を確認しましょう。この例はR言語のgmmパッケージのVignettesから持ってきました。
正規分布の一次モーメント条件は
$$
\mu = \mathbb{E}(x_i)
$$
二次モーメント条件は
$$
\sigma^2 = \mathbb{E}(x_i - \mu)^2
$$
三次モーメント条件は
$$
\mathbb{E}x_i^3 = \mu (\mu^2 + 3 \sigma^2)
$$
したがって、ベクトルでまとめて書くとこうなります:
\mathbb{E} \begin{bmatrix}
\mu - x_i \\
\sigma^2 - (x_i - \mu)^2 \\
x_i^3 - \mu (\mu^2 + 3\sigma^2)
\end{bmatrix} \equiv \mathbb{E}(m_i(\theta)) = 0
本記事では、一次モーメントと二次モーメントしか使わないベイズ一般化モーメント推定(gmm_normal_2)、一次から三次モーメントまで使うベイズ一般化モーメント推定(gmm_normal_3)、最後に正規分布の尤度を利用して普通に正規分布の平均をベイズの教科書通りに推定するモデル(real_normal)を比較します。
補足ですが、一般化モーメント法は、有限個のモーメント条件しか利用しません。一方、尤度関数は確率分布が持つすべてのモーメントを含み、あらゆる情報を活用します。そのため、尤度関数のほうが圧倒的に多くの情報を利用することになります。
Stanによる実装コードはこちらです:
data {
int N;
vector[N] x;
}
parameters {
real mu;
real<lower=0> sigma;
}
model {
mu ~ normal(0, 10);
sigma ~ gamma(1, 1);
vector[2] moment = rep_vector(0.0, 2);
for (i in 1:N){
moment[1] += mu - x[i];
moment[2] += sigma^2 - (x[i] - mu)^2;
}
target += - 0.5 * ((1/sqrt(N)) * moment)' * ((1/sqrt(N)) * moment);
}
data {
int N;
vector[N] x;
}
parameters {
real mu;
real<lower=0> sigma;
}
model {
mu ~ normal(0, 10);
sigma ~ gamma(1, 1);
vector[3] moment = rep_vector(0.0, 3);
for (i in 1:N){
moment[1] += mu - x[i];
moment[2] += sigma^2 - (x[i] - mu)^2;
moment[3] += x[i]^3 - mu * (mu^2 + 3*sigma^2);
}
target += - 0.5 * ((1/sqrt(N)) * moment)' * ((1/sqrt(N)) * moment);
}
data {
int N;
vector[N] x;
}
parameters {
real mu;
real<lower=0> sigma;
}
model {
mu ~ normal(0, 10);
sigma ~ gamma(1, 1);
x ~ normal(mu, sigma);
}
シミュレーション結果
では、早速シミュレーションデータで性能を確認しましょう!正解データは平均1、標準偏差3の正規分布です。
set.seed(12345)
df_norm <- 500 |>
rnorm(n = _, mean = 1, sd = 3) |>
tibble::tibble(
x = _
)
m_gmm_normal_2_init <- cmdstanr::cmdstan_model("gmm_normal_2.stan")
m_gmm_normal_2_estimate <- m_gmm_normal_2_init$variational(
seed = 12345,
data = list(
N = nrow(df_norm),
x = df_norm$x
)
)
m_gmm_normal_3_init <- cmdstanr::cmdstan_model("gmm_normal_3.stan")
m_gmm_normal_3_estimate <- m_gmm_normal_3_init$variational(
seed = 12345,
data = list(
N = nrow(df_norm),
x = df_norm$x
)
)
m_real_normal_init <- cmdstanr::cmdstan_model("real_normal.stan")
m_real_normal_estimate <- m_real_normal_init$variational(
seed = 12345,
data = list(
N = nrow(df_norm),
x = df_norm$x
)
)
結果を確認しましょう:
> m_gmm_normal_2_estimate
variable mean median sd mad q5 q95
lp__ -6.55 -6.07 1.44 0.96 -9.53 -5.17
lp_approx__ -0.97 -0.68 1.01 0.71 -2.92 -0.05
mu 1.26 1.26 0.05 0.05 1.18 1.33
sigma 2.96 2.96 0.01 0.01 2.95 2.98
> m_gmm_normal_3_estimate
variable mean median sd mad q5 q95
lp__ -25.20 -24.01 9.37 9.24 -41.91 -11.96
lp_approx__ -0.91 -0.64 0.95 0.61 -2.70 -0.05
mu 1.22 1.22 0.00 0.00 1.22 1.22
sigma 2.96 2.96 0.00 0.00 2.95 2.96
> m_real_normal_estimate
variable mean median sd mad q5 q95
lp__ -1259.86 -1259.53 1.30 1.02 -1262.46 -1258.51
lp_approx__ -0.99 -0.69 0.98 0.70 -2.84 -0.05
mu 1.22 1.22 0.15 0.15 0.98 1.47
sigma 3.05 3.05 0.09 0.09 2.90 3.19
なんか、なんとも言えないですね、、、
なので、やはり前回の記事のように、この三つのモデルの性能を頻度論的な分布で確認しましょう。ここでは事後分布の平均だけでなく、信用区間のカバー範囲も確認します。
future::plan(future::multisession)
moment_simulation_results <- 1000 |>
seq_len() |>
furrr::future_map(
\(i){
df_norm <- 500 |>
rnorm(n = _, mean = 1, sd = 3) |>
tibble::tibble(
x = _
)
m_gmm_normal_2_summary <- m_gmm_normal_2_init$variational(
seed = 12345,
data = list(
N = nrow(df_norm),
x = df_norm$x
)
)$
summary()
m_gmm_normal_3_summary <- m_gmm_normal_3_init$variational(
seed = 12345,
data = list(
N = nrow(df_norm),
x = df_norm$x
)
)$
summary()
m_real_normal_summary <- m_real_normal_init$variational(
seed = 12345,
data = list(
N = nrow(df_norm),
x = df_norm$x
)
)$
summary()
return(
list(
gmm_normal_2_mean = m_gmm_normal_2_summary |>
dplyr::filter(variable == "mu") |>
dplyr::pull(mean),
gmm_normal_2_q5 = m_gmm_normal_2_summary |>
dplyr::filter(variable == "mu") |>
dplyr::pull(q5),
gmm_normal_2_q95 = m_gmm_normal_2_summary |>
dplyr::filter(variable == "mu") |>
dplyr::pull(q95),
gmm_normal_3_mean = m_gmm_normal_3_summary |>
dplyr::filter(variable == "mu") |>
dplyr::pull(mean),
gmm_normal_3_q5 = m_gmm_normal_3_summary |>
dplyr::filter(variable == "mu") |>
dplyr::pull(q5),
gmm_normal_3_q95 = m_gmm_normal_3_summary |>
dplyr::filter(variable == "mu") |>
dplyr::pull(q95),
real_normal_mean = m_real_normal_summary |>
dplyr::filter(variable == "mu") |>
dplyr::pull(mean),
real_normal_q5 = m_real_normal_summary |>
dplyr::filter(variable == "mu") |>
dplyr::pull(q5),
real_normal_q95 = m_real_normal_summary |>
dplyr::filter(variable == "mu") |>
dplyr::pull(q95)
)
)
},
.progress = TRUE,
.options = furrr::furrr_options(seed = 12345)
)
まず可視化しましょう;
moment_simulation_results |>
dplyr::bind_rows() |>
dplyr::select(dplyr::ends_with("_mean")) |>
`colnames<-`(c("gmm_normal_2", "gmm_normal_3", "real_normal")) |>
dplyr::mutate(
rid = dplyr::row_number()
) |>
tidyr::pivot_longer(!rid, names_to = "variable", values_to = "mean") |>
dplyr::left_join(
moment_simulation_results |>
dplyr::bind_rows() |>
dplyr::select(dplyr::ends_with("_q5")) |>
`colnames<-`(c("gmm_normal_2", "gmm_normal_3", "real_normal")) |>
dplyr::mutate(
rid = dplyr::row_number()
) |>
tidyr::pivot_longer(!rid, names_to = "variable", values_to = "q5"),
by = c("rid", "variable")
) |>
dplyr::left_join(
moment_simulation_results |>
dplyr::bind_rows() |>
dplyr::select(dplyr::ends_with("_q95")) |>
`colnames<-`(c("gmm_normal_2", "gmm_normal_3", "real_normal")) |>
dplyr::mutate(
rid = dplyr::row_number()
) |>
tidyr::pivot_longer(!rid, names_to = "variable", values_to = "q95"),
by = c("rid", "variable")
) |>
ggplot2::ggplot() +
ggplot2::geom_point(ggplot2::aes(x = mean, y = rid)) +
ggplot2::geom_errorbarh(ggplot2::aes(xmin = q5, xmax = q95, y = rid), height = 0.2, color = ggplot2::alpha("blue", 0.3)) +
ggplot2::geom_vline(xintercept = 1, linetype = "dashed", color = "red", linewidth = 1.5) +
ggplot2::facet_wrap(~ variable, scales = "free_x") +
ggplot2::labs(y = "", x = "Estimated Value", title = "Simulation Results by Model") +
ggplot2::theme(
axis.text.y = ggplot2::element_blank(), # remove y-axis text
axis.ticks.y = ggplot2::element_blank(), # remove y-axis ticks
axis.title.y = ggplot2::element_blank(), # remove y-axis title (already done)
panel.grid.major.y = ggplot2::element_blank(), # remove major y grid lines
panel.grid.minor.y = ggplot2::element_blank() # remove minor y grid lines
)
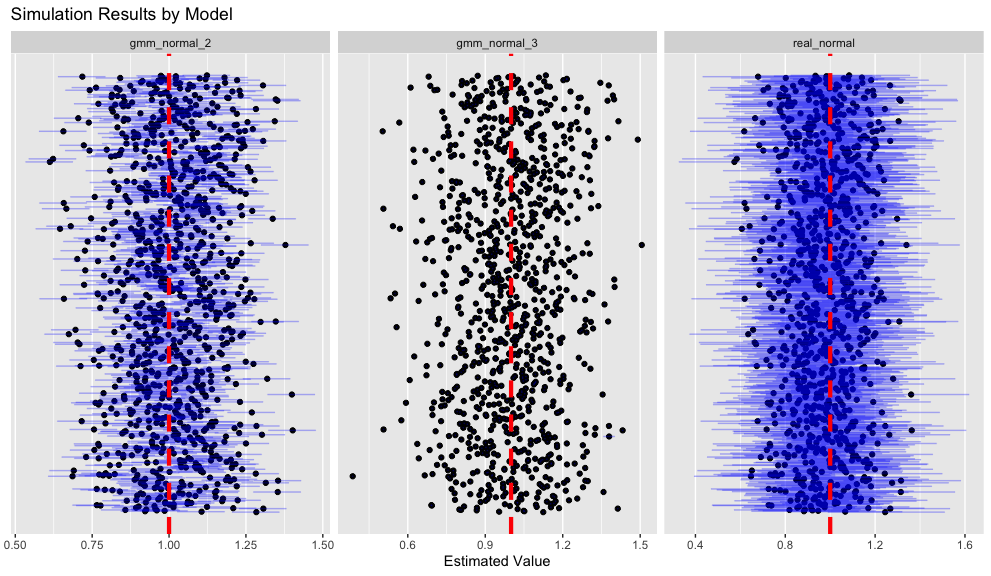
どのモデルにおいても、事後分布の平均は正解値である1の付近に分布しています。ただし、三次モーメントまでを用いるモデル(gmm_model_3)では、信用区間の幅がほとんどなく、推定の精度が非常に高いことが確認できます。二次モーメントまでを用いるモデル(gmm_model_2)も、gmm_model_3 ほどではないものの、比較的狭い信用区間を持っていますが、一部のサンプルでは正解値 1 をカバーしていないことがわかります。一方、尤度関数をそのまま用いたモデル(real_normal)は信用区間が最も広く、多くのサンプルで1を適切にカバーしている様子が視覚的に確認できます。
目検だけで判断するのはあまり客観的ではないため、ここで実際に信用区間が1をカバーした割合(include_ratio)と事後分布の平均の正解(1)に対する平均二乗誤差(mean_squared_error)をモデル別に計算します:
> moment_simulation_results |>
dplyr::bind_rows() |>
dplyr::select(dplyr::ends_with("_mean")) |>
`colnames<-`(c("gmm_normal_2", "gmm_normal_3", "real_normal")) |>
dplyr::mutate(
rid = dplyr::row_number()
) |>
tidyr::pivot_longer(!rid, names_to = "variable", values_to = "mean") |>
dplyr::left_join(
moment_simulation_results |>
dplyr::bind_rows() |>
dplyr::select(dplyr::ends_with("_q5")) |>
`colnames<-`(c("gmm_normal_2", "gmm_normal_3", "real_normal")) |>
dplyr::mutate(
rid = dplyr::row_number()
) |>
tidyr::pivot_longer(!rid, names_to = "variable", values_to = "q5"),
by = c("rid", "variable")
) |>
dplyr::left_join(
moment_simulation_results |>
dplyr::bind_rows() |>
dplyr::select(dplyr::ends_with("_q95")) |>
`colnames<-`(c("gmm_normal_2", "gmm_normal_3", "real_normal")) |>
dplyr::mutate(
rid = dplyr::row_number()
) |>
tidyr::pivot_longer(!rid, names_to = "variable", values_to = "q95"),
by = c("rid", "variable")
) |>
dplyr::mutate(
include = (1 - q95) * (1 - q5) < 0,
squared_error = (1 - mean) ^ 2
) |>
dplyr::summarise(
include_ratio = mean(include),
mean_squared_error = mean(squared_error),
.by = variable
)
# A tibble: 3 × 3
variable include_ratio mean_squared_error
<chr> <dbl> <dbl>
1 gmm_normal_2 0.421 0.0190
2 gmm_normal_3 0.009 0.0292
3 real_normal 0.929 0.0197
尤度を利用したモデル(real_normal)は最も高いカバー率を示しており、全体の約93%のサンプルにおいて、信用区間が正解値である1を含んでいます。gmm_normal_2 のカバー率は42%にとどまり、gmm_normal_3 に至っては10%を下回っています。平均二乗誤差に関しては、real_normal と gmm_normal_2 の間に大きな差は見られませんが、gmm_normal_3 の推定精度は著しく低く、他のモデルに比べて劣っています。
シミュレーションの結果を踏まえると、筆者の実装に問題がない限り、以下のような示唆が得られると考えられます:
- 確率モデルが分かっている場合は、モーメント条件よりも尤度を用いるべきである
- モーメント条件を増やせば必ずしも推定精度が向上するとは限らない
結論
いかがでしたでしょうか?本記事では、もし尤度が既知である、あるいは分析上合理的に仮定できる(たとえば、データが正規分布やポワソン分布に従うといったケース)のであれば、ベイズ一般化モーメント法を用いるべきではないということを、シミュレーションを通じて示しました。
今後は、尤度を仮定せず、経済学的理論に基づいて導出されたモーメント条件のみを用いてベイズ一般化モーメント法を活用するアプローチについて、別の記事で紹介する予定です。ぜひご期待ください。
最後に、私たちと一緒に働きたい方はぜひ下記のリンクもご確認ください: