はじめまして、りょーつといいます。高専出身の大学院1年生です。研究の専門は力学や機構学で、Qiitaでは主に制御工学や数学に関する記事を書いています。
本稿はスクリュー理論の解説(布教)をする7つ目の記事です。前回までの記事は以下のリンクを参照してください。
スクリュー理論① 外積の歪対称行列表現
スクリュー理論② 行列の指数関数
スクリュー理論③ 行列指数と回転行列の関係
スクリュー理論④ 回転行列の成分表示
スクリュー理論⑤ 回転行列による座標系の表現
スクリュー理論⑥ 剛体の速度・加速度の座標変換公式の導出
スクリュー理論は剛体の運動を記述する手法で、ロボット工学などでよく使われています。日本の高専や大学ではDH法を使った記述を学ぶことが多いですが、国際的にはスクリュー理論を使った記述が一般的となってきているようです。スクリュー理論を扱う日本語の文献は少ないので、この記事が誰かの助けになればいいなと思います。
目次
1. はじめに
本稿では三次元空間における右手系の回転行列について紹介します。基本的な内容は以前の記事と同様ですが、三次元になっている分、難易度が上がります。特に右手系と左手系の違いについて触れられたらいいなと思っています。
2. 右手系の回転行列の定義
本章では右手系の三次元回転行列の定義を紹介します。以下の2式を満たす$3\times 3$行列$R$が右手系の三次元回転行列となります。
R^T R \
=
I
\tag{1}
\det{R} \
=
1
\tag{2}
ただし$I$は単位行列です。
では(1)、(2)式の意味を考えてみましょう。まず(1)式は、互いに直交する3つの単位ベクトルが並ぶことで回転行列$R$が構成されることを意味しています。これは、回転行列$R$そのものが正規直行基底を表していることになります。本当にそうなのか確かめてみましょう。
3つの互いに直交する三次元単位縦ベクトル$\boldsymbol{u_i}\in \mathbb{R} ^ 3\ \ (i = 1,2,3)$を考えます。このとき$\boldsymbol{u_i}$が単位ベクトルであることと、$\boldsymbol{u_i}$と$\boldsymbol{u_j}\ \ (i \neq j)$が互いに直交することを式で表すと以下のようになります。
\boldsymbol{u_i}^T \boldsymbol{u_i} \
=
1
\ \ (i = 1,2,3)
\tag{3}
\boldsymbol{u_i}^T \boldsymbol{u_j} \
=
0
\ \ (i \neq j)
\tag{4}
また、クロネッカーのデルタ$\delta_{ij}$を用いることで(3)(4)式は以下のようにまとめることができます。
\boldsymbol{u_i}^T \boldsymbol{u_j} \
=
\delta_{ij}
\tag{5}
(5)式のような特性をもつ単位ベクトル$\boldsymbol{u_i}$を使って、行列$A$を
A
=
\begin{bmatrix}
\boldsymbol{u_1} & \boldsymbol{u_2} & \boldsymbol{u_3}\\
\end{bmatrix}
\tag{6}
のように定義したとします。行列$A$に対して(1)式と同様の操作を行うと
A^T A \
=
\begin{bmatrix}
\boldsymbol{u_1}^T \\
\boldsymbol{u_2}^T \\
\boldsymbol{u_3}^T \\
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{u_1} & \boldsymbol{u_2} & \boldsymbol{u_3}\\
\end{bmatrix}
=
\begin{bmatrix}
\delta_{11} & \delta_{12} & \delta_{13}\\
\delta_{21} & \delta_{22} & \delta_{23}\\
\delta_{31} & \delta_{32} & \delta_{33}\\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1\\
\end{bmatrix}
=
I
\tag{7}
となり、たしかに互いに直交する3つの単位ベクトルが並ぶことで回転行列$R$が構成されることをフワッと確認することができました。
次に(2)式の意味を考えたいと思います。(2)式は(6)式のように直交行列を定義したとき、単位ベクトルの間に
\boldsymbol{u_1} \times \boldsymbol{u_2}
=
\boldsymbol{u_3}
\tag{8}
の関係があることを意味しています。実際に確かめてみましょう。ここで
\boldsymbol{u_1}
=
\begin{bmatrix}
u_{11} \\
u_{21} \\
u_{31} \\
\end{bmatrix}
\tag{9}
\boldsymbol{u_2}
=
\begin{bmatrix}
u_{12} \\
u_{22} \\
u_{32} \\
\end{bmatrix}
\tag{10}
とすると、(8)式の仮定より
\boldsymbol{u_3}
=
\begin{bmatrix}
u_{13} \\
u_{23} \\
u_{33} \\
\end{bmatrix}
=
\begin{bmatrix}
u_{21} u_{32} - u_{31} u_{22} \\
u_{31} u_{12} - u_{11} u_{32} \\
u_{11} u_{22} - u_{21} u_{12} \\
\end{bmatrix}
\tag{11}
が得られます。あとは(2)式と同様に行列式を計算してみましょう。少し展開が大変ですが、以下のような結果が得られます。
\det{A}
=
\begin{vmatrix}
u_{11} & u_{12} & u_{21} u_{32}\\
u_{21} & u_{22} & u_{31} u_{12}\\
u_{31} & u_{32} & u_{11} u_{22}\\
\end{vmatrix}
-
\begin{vmatrix}
u_{11} & u_{12} & u_{31} u_{22} \\
u_{21} & u_{22} & u_{11} u_{32} \\
u_{31} & u_{32} & u_{21} u_{12} \\
\end{vmatrix}
=
u_{11}(u_{11}{u_{22}}^2 - u_{12} u_{31} u_{32})
- u_{21}(u_{11} u_{12} u_{22} - u_{21} {u_{32}}^2)
+ u_{31}({u_{12}}^2 u_{31} - u_{21} u_{22} u_{32})
- u_{11}(u_{12} u_{21} u_{22} - u_{11} {u_{32}}^2)
+ u_{21}({u_{12}}^2 u_{21} - u_{22} u_{31} u_{32})
- u_{31}(u_{11} u_{12} u_{32} - {u_{22}}^2 u_{31})
=
{(u_{11}u_{22})}^2 - 2(u_{11}u_{22})(u_{12}u_{21}) + {(u_{12}u_{21})}^2
+
{(u_{21}u_{32})}^2 - 2(u_{21}u_{32})(u_{22}u_{31}) + {(u_{22}u_{31})}^2
+
{(u_{12}u_{31})}^2 - 2(u_{12}u_{31})(u_{11}u_{32}) + {(u_{11}u_{32})}^2
=
{(u_{11}u_{22} - u_{12}u_{21})}^2
+
{(u_{21}u_{32} - u_{22}u_{31})}^2
+
{(u_{12}u_{31} - u_{11}u_{32})}^2
=
{u_{13}}^2
+
{u_{23}}^2
+
{u_{33}}^2
=
\boldsymbol{u_3}^T \boldsymbol{u_3}
=
\delta_{33}
=
1
\therefore \ \
\det{A}
=
1
\tag{12}
たしかに行列式の計算結果が$1$になることが分かりました。この結果の意味を図的に考えてみたいと思います。
3つの互いに直交する三次元単位縦ベクトル$\boldsymbol{v_i}\in \mathbb{R} ^ 3\ \ (i = 1,2,3)$とそれらを並べて以下のように定義される行列$B$を考えます。
B
=
\begin{bmatrix}
\boldsymbol{v_1} & \boldsymbol{v_2} & \boldsymbol{v_3}\\
\end{bmatrix}
\tag{13}
ここで$\boldsymbol{v_i}$には(8)式とは異なり、
\boldsymbol{v_3}
=
\boldsymbol{v_2} \times \boldsymbol{v_1}
\tag{14}
の関係がある場合を考えてみます。外積の順番が逆になっていることに注意です。このときの行列式を計算すると、(2)式の関係から
\det{B}
=
\begin{vmatrix}
\boldsymbol{v_1} & \boldsymbol{v_2} & \boldsymbol{v_3}\\
\end{vmatrix}
=
\begin{vmatrix}
\boldsymbol{v_1} & \boldsymbol{v_2} & \boldsymbol{v_2} \times \boldsymbol{v_1}\\
\end{vmatrix}
=
-
\begin{vmatrix}
\boldsymbol{v_1} & \boldsymbol{v_2} & \boldsymbol{v_1} \times \boldsymbol{v_2}\\
\end{vmatrix}
=
-1
\tag{15}
となり、計算結果が$1$にならないことが分かりました。(12)式と(15)式の結果より、互いに直交する単位ベクトルを並べて行列を構成したとしても、3本目の基底の向きに応じて右手系の回転行列に属するか変化することが分かります。
では、行列$B$のように
C^T C = I
\tag{16}
\det{C} = -1
\tag{17}
を満たすものは何なのでしょうか。(16)(17)式の双方を満たす$3\times 3$行列$C$は左手系の三次元回転行列となります。このことをまとめたものが図1になります。
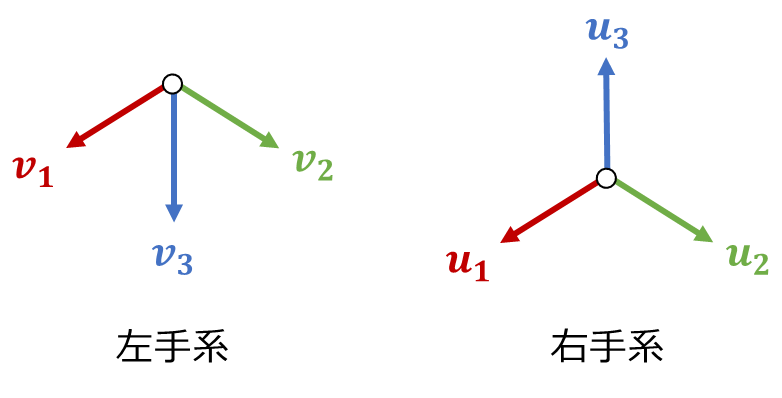
図1 三次元回転行列の右手系と左手系
回転行列の定義として(1)(2)式を用いることが多いですが、これは世の中で右手系がよく使われているからです。実際には(1)式が回転行列の定義であり、(2)式は回転行列の内、右手系となるものを絞りこむための条件となります。
これらのことから2次元の場合と同様に、右手座標系は右手系の回転行列、左手座標系は左手系の回転行列で表現できることが分かりました。
3. おわりに
本稿では三次元回転行列の定義と右手系・左手系についてフワッと紹介しました。次回以降は回転行列を用いた座標変換について紹介し、演算子としての扱い方についてお話できたらいいなあと考えています。
最後まで読んでいただき、ありがとうございました!