スクリュー理論⑤ 回転行列による座標系の表現

　はじめまして、りょーつといいます。高専出身の大学院1年生です。研究の専門は力学や機構学で、Qiitaでは主に制御工学や数学に関する記事を書いています。
　本稿はスクリュー理論の解説(布教)をする5つ目の記事です。前回までの記事は以下のリンクを参照してください。

スクリュー理論① 外積の歪対称行列表現
スクリュー理論② 行列の指数関数
スクリュー理論③ 行列指数と回転行列の関係
スクリュー理論④ 回転行列の成分表示

スクリュー理論は剛体の運動を記述する手法で、ロボット工学などでよく使われています。日本の高専や大学ではDH法を使った記述を学ぶことが多いですが、国際的にはスクリュー理論を使った記述が一般的となってきているようです。スクリュー理論を扱う日本語の文献は少ないので、この記事が誰かの助けになればいいなと思います。

目次

1.はじめに
2.回転行列の定義
3.回転行列による座標系の表現
4.おわりに

1. はじめに

　本稿では回転行列を用いた座標系の表現について紹介します。回転行列という名前から、回転にかかわってそうなイメージが付きがちですが、回転行列が座標系そのものを表しているというイメージが伝わればうれしいです。行列演算の知識を使用します。

2. 回転行列の定義

　前回の記事で回転行列の成分表示をしましたが、「回転行列とはなにか？」という点についてはあまり触れていなかったのでここでフワッと説明していきます。今回は2次元空間における右手系の回転行列を考えます。2次元空間における回転行列は互いに直交する大きさが1のベクトルを2つ、行列式が1になるように並べて作られる行列です。例えば2次元の縦ベクトル$\boldsymbol{u_1}\in \mathbb{R} ^ 2$と$\boldsymbol{u_2}\in \mathbb{R} ^ 2$がそれぞれ

\boldsymbol{u_1}
\perp
\boldsymbol{u_2}
\ \ \
\Leftrightarrow
\ \ \
\boldsymbol{u_1} \cdot \boldsymbol{u_2}
=
0
\tag{1}

||\boldsymbol{u_1}||
=
1
\ \ \
\Leftrightarrow
\ \ \
\boldsymbol{u_1} \cdot \boldsymbol{u_1}
=
1
\tag{2}

||\boldsymbol{u_2}||
=
1
\ \ \
\Leftrightarrow
\ \ \
\boldsymbol{u_2} \cdot \boldsymbol{u_2}
=
1
\tag{3}

を満たすとき、

A
=
\begin{bmatrix}
\boldsymbol{u_1} & \boldsymbol{u_2}\\
\end{bmatrix}
\tag{4}

のような$2\times 2$行列$A$は2次元空間における回転行列の候補となります。回転行列$\rm{A}$には以下の2つの性質があります。

A^\rm{T} A \ 
=
I
\tag{5}

\det({A}) \ 
=
1
\tag{6}

ただし$I$は単位行列を意味します。(1)~(4)式に示した性質をもとに(5)式を導出してみましょう。(1)~(3)式で表した直交性をもとに(5)式の左辺を計算してみると

A^\rm{T} A \ 
=
\Bigg[
\begin{matrix}
\boldsymbol{u_1}^\rm{T} \\
\boldsymbol{u_2}^\rm{T} \\
\end{matrix}
\Bigg]
\begin{bmatrix}
\boldsymbol{u_1} & \boldsymbol{u_2}\\
\end{bmatrix}
=
\Bigg[
\begin{matrix}
\boldsymbol{u_1}^\rm{T} \boldsymbol{u_1} &  \boldsymbol{u_1}^\rm{T} \boldsymbol{u_2}\\
\boldsymbol{u_2}^\rm{T} \boldsymbol{u_1} &  \boldsymbol{u_2}^\rm{T} \boldsymbol{u_2}\\
\end{matrix}
\Bigg]
=
\begin{bmatrix}
\boldsymbol{u_1}\cdot \boldsymbol{u_1} & \boldsymbol{u_1}\cdot \boldsymbol{u_2}\\
\boldsymbol{u_2}\cdot \boldsymbol{u_1} & \boldsymbol{u_2}\cdot \boldsymbol{u_2}\\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0\\
0 & 1\\
\end{bmatrix}
=
I
\tag{7}

となり、(5)式が導出されます。行列式の性質より

\det({A^\rm{T}}) \ 
=
\det({A})
\tag{8}

であることに注意して(5)式の両辺の行列式を計算してみます。左辺は

\det({A^\rm{T} A}) \ 
=
\det({A^\rm{T}}) \det({A})
= (\det{A})^2
\tag{9}

になります。一方右辺は明らかに

\det(I) \ 
=
1
\tag{10}

です。(9)式と(10)式をつなげると

(\det{A})^2 
=
1

\therefore
\det{A} 
=
\pm \ 1

\tag{11}

が得られます。(11)式は(6)式に似た形をしていますが、"$-1$"を含んでいるので証明達成とはなりませんでした...ではここで(11)式の意味を考えてみたいと思います。(4)式の説明のところで回転行列を作るベクトル$\boldsymbol{u_1}$と$\boldsymbol{u_2}$の並べる順番に注意が必要だと述べました。この性質が"$-1$"に関係します。ためしに(4)式とは異なる並べ方をした行列$B$を考えてみましょう。

B
=
\begin{bmatrix}
\boldsymbol{u_2} & \boldsymbol{u_1}\\
\end{bmatrix}
\tag{12}

行列$B$の行列式を計算すると交換則より以下の関係が得られます。

\det({B})
=
\begin{vmatrix}
\boldsymbol{u_2} & \boldsymbol{u_1}\\
\end{vmatrix}
=
-
\begin{vmatrix}
\boldsymbol{u_1} & \boldsymbol{u_2}\\
\end{vmatrix}
=
-\det({A})
\tag{13}

(13)式より、ベクトルの並べ方を間違えると行列式が"$-1$"になってしまうことが分かります。次章でもう少し詳細な説明を書くので、まずは回転行列は互いに直交する大きさが1のベクトルを2つ、行列式が1になるように並べて作られる行列ということを抑えておいてください。(数式的には(5)式と(6)式を満たす行列が回転行列として定義されます。)

3. 回転行列による座標系の表現

　本章では回転行列の図的イメージを示し、座標系の表現とのつながりについて説明します。おさらいになりますが、回転行列$A$の定義は互いに直交する大きさが1のベクトル$\boldsymbol{u_1}$と$\boldsymbol{u_2}$を行列式が1になるように並べて作られる行列です。まずはこの定義のうち互いに直交する大きさが1のベクトルの部分に注目してみます。図で表すときっと以下のようになりますね。

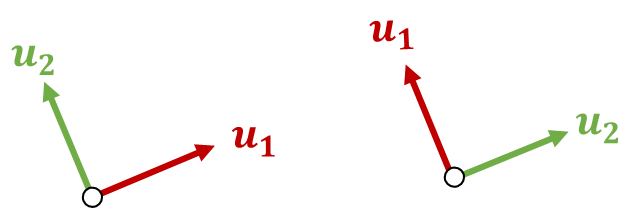
図1　回転行列を構成するベクトル

図1より、回転行列は座標系を表していることが分かります。なんとなくイメージはつかめましたが、「どんな順番で座標軸を取るか?」という問題が残っています。この説明のために以下の簡単な問題を考えてみてください。

Q. 図2に示す2つの$x-y$座標系のうち、直観的に好きなのはどちらですか？

図2　右手系と左手系

　おそらく多くの人は$x$軸が右を向いているものを選択したかと思います。$x$軸が左を向いていたとしても本質的な問題はないのですが、なんだか$x$軸が右を向いているほうが直観的に分かりやすいですよね。ちなみに上の図において$x$軸が右を向いているものは右手系、左を向いているものは左手系と呼ばれています。
　このように座標系をつくるときは基底の"並び方"が重要となります。ロボットの分野でも右手系を使うことが多いので、図1のうち右手系となるもののみを選別できるように条件を追加しないといけません。そうして追加されたのが(6)式です。まとめると(5)式を満たす行列は回転行列であり、追加で(6)式を満たすものが右手系の回転行列ということになります。(ちなみに(5)式を満たした上で行列式が$-1$になると左手系を意味します。)

では、互いに直交するベクトル$\boldsymbol{u_1}$と$\boldsymbol{u_2}$をどのように並べれば右手系の回転行列(行列式が1になる行列)を作れるのでしょうか？説明のために回転行列の1列目に配置されるベクトルを1つ目の基底、2列目に配置されるベクトルを2つ目の基底とします。このとき2つ目の基底が1つ目の基底を半時計まわりに回転させた方向を向いていたら右手系となります。

　なんとなく雰囲気を感じ取ってもらうためにたくさんの例を用意しました。

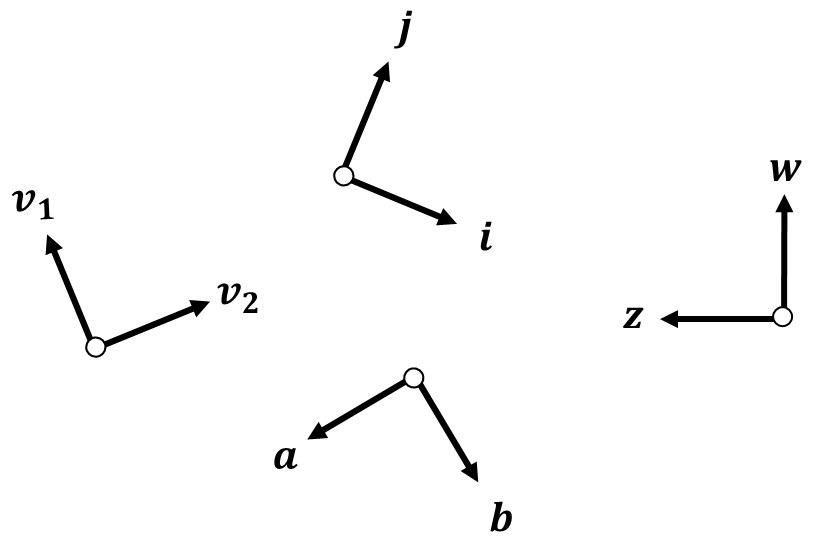
図3からは以下の回転行列が得られます。

A_1
=
\begin{bmatrix}
\boldsymbol{i} & \boldsymbol{j}\\
\end{bmatrix}
\tag{14}

A_2
=
\begin{bmatrix}
\boldsymbol{v_2} & \boldsymbol{v_1}\\
\end{bmatrix}
\tag{15}

A_2
=
\begin{bmatrix}
\boldsymbol{w} & \boldsymbol{z}\\
\end{bmatrix}
\tag{16}

A_2
=
\begin{bmatrix}
\boldsymbol{a} & \boldsymbol{b}\\
\end{bmatrix}
\tag{17}

右手系の回転行列のノリが伝わったでしょうか..?このノリは今後3次元空間の回転行列を扱う際にも必要になってきます。

4. おわりに

　本稿では2次元空間に限定し、回転行列の定義とともに、その図的イメージを踏まえて座標系との対応関係を紹介しました。うまく文章に落とし込むのが難しい内容でしたので、分かりづらい部分もあったかもしれません。適宜更新していくのでなにかの理解の助けになれば幸いです。来週は本記事をもとに3次元空間の回転行列について考えていこうと思います。
　最後まで読んでいただきありがとうございました(^^)