スクリュー理論① 外積の歪対称行列表現

　はじめまして、りょーつといいます。高専出身の大学院1年生です。研究の専門は力学や機構学で、主に制御工学や数学に関する記事を書いています。
　これから何回かに分けてスクリュー理論の解説(布教)をしたいと思っています。スクリュー理論は剛体の運動を記述する手法で、ロボット工学などで使われています。日本の高専や大学ではDH法を使った記述を学ぶことが多いですが、国際的にはスクリュー理論を使った記述が一般的となってきているようです。自分の出身大学では、2022年度から工学部のカリキュラムにスクリュー理論が取り入れられるようになりました。スクリュー理論を扱う日本語の文献は少ないので、この記事が誰かの助けになればいいなと思います。

目次

1.はじめに
2.ベクトルの線形写像
3.三次元ベクトルの外積
4.外積の歪対称行列表現
5.おわりに

1. はじめに

　本稿では三次元ベクトルの外積演算が線形写像とみなせることを示し、その変換行列を導出します。また、変換行列が歪対称行列であることも確認します。
　線形代数の知識をすこし使います。本記事ではあまり厳密なことは書かず、フワッと受け入れられるような内容を目指します。

2. ベクトルの線形写像

　まずは写像についてフワッと説明します。AIとおしゃべりすることを想像してみてください。AIにベクトル$\boldsymbol{x}$を食わせるとベクトル$\boldsymbol{y}$が出力されるとします。このときベクトル$\boldsymbol{y}$の生成方法にルールが存在すれば、このAIはベクトルの「写像」と呼ばれます。

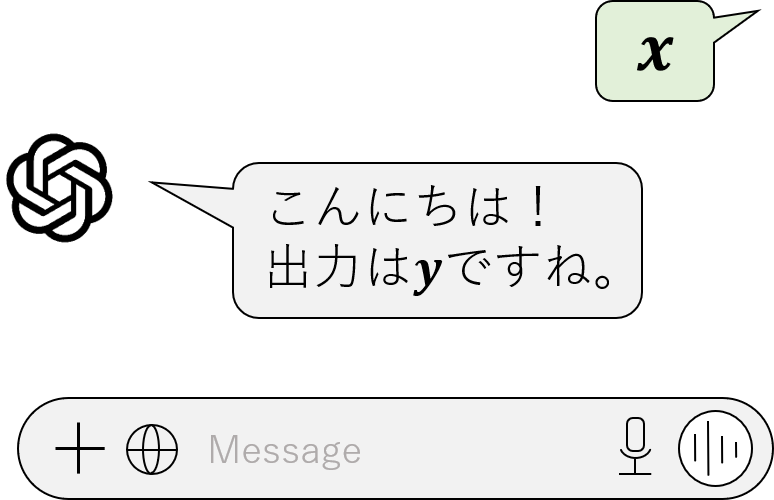
図1　$\boldsymbol{x}$を食わせると$\boldsymbol{y}$を出力する生成AI

　生成方法のルールは入力されるベクトル$\boldsymbol{x}$に関連するものであればなんでもよく、例えば入力したベクトルの全成分を2倍するとか、向きを反転させるとかいろいろ考えられます。写像を$f$と表記するのであれば、ベクトル$\boldsymbol{x}$とベクトル$\boldsymbol{y}$の関係は以下のように表せます。

\boldsymbol{y}
= 
f(\boldsymbol{x})
\tag{1}

　写像の中にもいろいろ種類があり、その中でも以下のルールを満たすものが線形写像と呼ばれます。

①$f(\boldsymbol{0})=\boldsymbol{0}$
②$f(k\boldsymbol{a})=kf(\boldsymbol{a})$
③$f(\boldsymbol{b} + \boldsymbol{c})=f(\boldsymbol{b}) + f(\boldsymbol{c})$

上の3つをざっくり文章で説明すると

①零ベクトルを入力すると零ベクトルが出力される
②入力が$k$倍されると出力も$k$倍される
③ベクトルの和$\boldsymbol{b} + \boldsymbol{c}$を入力したとき、出力はそれぞれの出力の和$f(\boldsymbol{b}) + f(\boldsymbol{c})$に分解できる

となります。これらの条件を満たす線形写像は表現行列と呼ばれる行列$T$を使って

\boldsymbol{y}
= 
T\boldsymbol{x}
\tag{2}

のように写像$f$を表現できます。

3. 三次元ベクトルの外積

　外積は2つのベクトルを入力し、1つのベクトルを出力する演算です。表記には$\boldsymbol{\times}$や$\boldsymbol{\wedge}$という記号を使います。$\boldsymbol{\wedge}$は高次元を扱う場合に使用される記号で、工学分野では$\boldsymbol{\times}$が一般的に使用されます。2つのベクトル$\boldsymbol{a}$と$\boldsymbol{b}$の外積を$\boldsymbol{c}$とするとき、以下のような数式で表されます。

\boldsymbol{c}
= 
\boldsymbol{a}
\times
\boldsymbol{b}
\tag{3}

では、外積によってどんなベクトル$\boldsymbol{c}$が得られるのでしょうか？外積の計算結果$\boldsymbol{c}$は以下に示す特徴を有することが知られています。

㋐ 出力ベクトル$\boldsymbol{c}$は2つの入力ベクトル$\boldsymbol{a}$, $\boldsymbol{b}$の両方に直交する。
㋑ 出力ベクトル$\boldsymbol{c}$の大きさは$\lVert\boldsymbol{c}\rVert = \lVert\boldsymbol{a}\rVert \lVert\boldsymbol{b}\rVert \sin{\phi}$で計算される。ただし$\phi$は$\boldsymbol{a}$と$\boldsymbol{b}$のなす角である。
㋒ 出力ベクトル$\boldsymbol{c}$の向きは1つ目の入力$\boldsymbol{a}$から2つ目の入力$\boldsymbol{c}$に向かって右ねじを回転させたときにねじが進む方向である。

文章で書いても分かりづらいので㋐～㋒を直観的に示した図を貼っておきます。

図2　㋐ 外積の出力$\boldsymbol{c}$は2つの入力$\boldsymbol{a}$, $\boldsymbol{b}$の両方に直交する。

図3　㋑ 外積の出力$\boldsymbol{c}$の大きさは$\lVert\boldsymbol{c}\rVert = \lVert\boldsymbol{a}\rVert \lVert\boldsymbol{b}\rVert \sin{\phi}$で計算される。ただし$\phi$は$\boldsymbol{a}$と$\boldsymbol{b}$のなす角である。

図4　㋒ 出力$\boldsymbol{c}$の向きは1つ目の入力$\boldsymbol{a}$から2つ目の入力$\boldsymbol{c}$に向かって右ねじを回転させたときにねじが進む方向である。

　外積によって得られるベクトル$\boldsymbol{c}$の具体的な計算方法は以下の行列式で表されます。

\boldsymbol{c}
= 
\begin{vmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
\end{vmatrix}
\tag{4}

ただし

\boldsymbol{a}
= 
a_1\boldsymbol{i} + a_2\boldsymbol{j} + a_3\boldsymbol{k} \\
\tag{5}

\boldsymbol{b}
= 
b_1\boldsymbol{i} + b_2\boldsymbol{j} + b_3\boldsymbol{k} \\
\tag{5}

\boldsymbol{c}
= 
c_1\boldsymbol{i} + c_2\boldsymbol{j} + c_3\boldsymbol{k} \\
\tag{7}

とし、$\boldsymbol{i}$, $\boldsymbol{j}$, $\boldsymbol{k}$を正規直交基底とします。なお、行列式中の$\boldsymbol{i}$, $\boldsymbol{j}$, $\boldsymbol{k}$はただの記号とみなして計算します。
　外積は通常、2つのベクトルから1つのベクトルを出力する演算ですが、ここでは入力ベクトルを1つ固定し、1つのベクトルから1つのベクトルを出力する演算とみなしてみることにします。具体的には定ベクトルを$\boldsymbol{a}$、入力ベクトルを$\boldsymbol{x}$、出力ベクトルを$\boldsymbol{y}$としたときに

\boldsymbol{y}
= 
\boldsymbol{a}
\times
\boldsymbol{x}
\tag{8}

という外積を考えれば、1つのベクトルから1つのベクトルを出力する演算とみなせますね。(8)式はあるベクトル$\boldsymbol{x}$を入力することでベクトル$\boldsymbol{y}$が出力されているので写像とみなすことができます。
　さらに(8)式はただの写像ではなく、線形写像となります。実際に確認してみましょう。前提として

\boldsymbol{x}
= 
x_1\boldsymbol{i} + x_2\boldsymbol{j} + x_3\boldsymbol{k} \\
\tag{9}

\boldsymbol{y}
= 
y_1\boldsymbol{i} + y_2\boldsymbol{j} + y_3\boldsymbol{k} \\
\tag{10}

とします。
まずは線形写像の条件①を確認します。入力ベクトル$\boldsymbol{x}$が零ベクトルの場合

\boldsymbol{y}
= 
\boldsymbol{a}
\times
\boldsymbol{0}
=
\begin{vmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_1 & a_2 & a_3 \\
0 & 0 & 0 \\
\end{vmatrix}
=
\boldsymbol{0}
\tag{11}

となり、たしかに零ベクトルが出力されます。
　次に条件②を確認します。$k$を定数とし、ベクトル($k\boldsymbol{x}$)を入力すると行列式の特性から

\boldsymbol{y}
= 
\boldsymbol{a}
\times
(k\boldsymbol{x})
=
\begin{vmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_1 & a_2 & a_3 \\
kx_1 & kx_2 & kx_3 \\
\end{vmatrix}
=
k\begin{vmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_1 & a_2 & a_3 \\
x_1 & x_2 & x_3 \\
\end{vmatrix}
=
k \bigl( \boldsymbol{a}
\times
\boldsymbol{x} \bigr)
\tag{12}

となり、たしかに入力と同様$k$倍のベクトルが出力されます。
　次に条件③を確認します。ベクトル$\boldsymbol{z}$を

\boldsymbol{z}
= 
z_1\boldsymbol{i} + z_2\boldsymbol{j} + z_3\boldsymbol{k} \\
\tag{13}

と定義し、ベクトル($\boldsymbol{x}+\boldsymbol{z}$)を入力すると行列式の特性から

\boldsymbol{y}
= 
\boldsymbol{a}
\times
(\boldsymbol{x} + \boldsymbol{z})
=
\begin{vmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_1 & a_2 & a_3 \\
x_1 + z_1 & x_2 + z_2 & x_3 + z_3 \\
\end{vmatrix}
=
\begin{vmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_1 & a_2 & a_3 \\
x_1 & x_2 & x_3 \\
\end{vmatrix}
+
\begin{vmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_1 & a_2 & a_3 \\
z_1 & z_2 & z_3 \\
\end{vmatrix}
=
\boldsymbol{a}
\times
\boldsymbol{x} 
+
\boldsymbol{a}
\times
\boldsymbol{z} 
\tag{14}

となり、たしかに各ベクトルの外積結果の和が出力されます。
　以上のことから定ベクトル$\boldsymbol{a}$との外積は線形写像であることが示せました。外積が線形写像ということは、(2)式のように表現行列$T$が存在するはずです。次章では外積の表現行列$T$を計算します。

4. 外積の歪対称行列表現

　外積演算の表現行列$T$を計算してみます。表現行列$T$は定ベクトル$\boldsymbol{a}$に依存するため、ここでは$T_a$と書くことにします。これまでのことをまとめると表現行列$T_a$は

\boldsymbol{y}
= 
T_a \boldsymbol{x}
= 
\boldsymbol{a}
\times
\boldsymbol{x}
\tag{15}

を満たします。実際に(15)式の右辺を計算して$T_a$を求めてみましょう

\boldsymbol{a}
\times
\boldsymbol{x}
=
\begin{vmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
a_1 & a_2 & a_3 \\
x_1 & x_2 & x_3 \\
\end{vmatrix}
=
\begin{vmatrix}
a_2 & a_3 \\
x_2 & x_3 \\
\end{vmatrix}
\boldsymbol{i}
-
\begin{vmatrix}
a_1 & a_3 \\
x_1 & x_3 \\
\end{vmatrix}
\boldsymbol{j}
+
\begin{vmatrix}
a_1 & a_2 \\
x_1 & x_2 \\
\end{vmatrix}
\boldsymbol{k}

=
\begin{bmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
\end{bmatrix}
\begin{bmatrix}
a_2 x_3 - a_3 x_2 \\
a_3 x_1 - a_1 x_3 \\
a_1 x_2 - a_2 x_1 \\
\end{bmatrix}
=
\begin{bmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
\end{bmatrix}
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
x_3 \\
\end{bmatrix}
\tag{16}

また、ベクトル$\boldsymbol{y}$は

\boldsymbol{y} 
=
\begin{bmatrix}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
\end{bmatrix}
\begin{bmatrix}
y_1 \\
y_2 \\
y_3 \\
\end{bmatrix}
\tag{17}

であるため、(16)式と(17)式の座標を比較すると

\begin{bmatrix}
y_1 \\
y_2 \\
y_3 \\
\end{bmatrix}
=
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
x_3 \\
\end{bmatrix}
=T_a
\begin{bmatrix}
x_1 \\
x_2 \\
x_3 \\
\end{bmatrix}

\therefore
T_a
=
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0 \\
\end{bmatrix}
\tag{18}

のように外積の表現行列$T_a$が得られます。ここで表現行列$T_a$の転置をとると

\therefore
{T_a}^T
=
-T_a
\tag{19}

という関係が得られます。(19)式の関係を満たす行列は歪対称行列と呼ばれ、外積を(15)式のように行列を使用して表記することを歪対称行列表現と言ったりします。外積演算の歪対称行列表現はスクリュー理論を学ぶ上で至るところに登場します。

5. おわりに

　本記事ではスクリュー理論を学ぶうえで重要な、外積の歪対称行列表現について紹介しました。来週は歪対称行列表現を使用してベクトルの回転運動を記述する方法について紹介したいと思っています。
　最後までよんでいただきありがとうございました(^^)