基礎的な強化学習アルゴリズムともいえる、SARSA,Q学習についての解説になります。
これからの強化学習という本の内容を参考にさせていただきました。
要点をまとめて、なるべく簡潔にPythonで実装したいと思います。
強化学習の基本的な枠組み
マルコフ決定過程(Markov Decision Process : MDP)
強化学習は、行動する主体であるエージェント、そのまわりの環境、そしてそれらの間の相互作用からなります。
この相互作用を表す数理モデルはいくつかありますが、一番有名なものに**マルコフ決定過程(Markov Decision Process: MDP)**というものがあります。
MDPは、状態空間S、行動空間A(s)、初期状態分布P0、状態遷移確率P(s'|s,a)、報酬関数r(s,a,s')の要素によって記述される確率過程です。
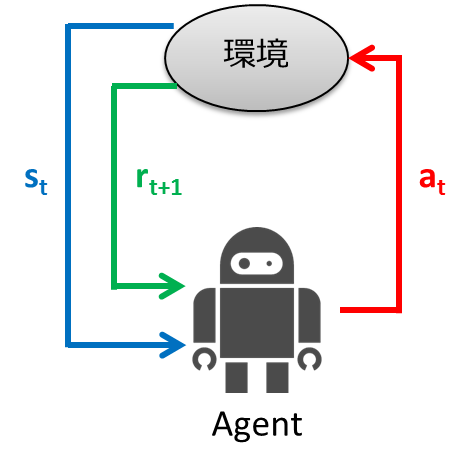
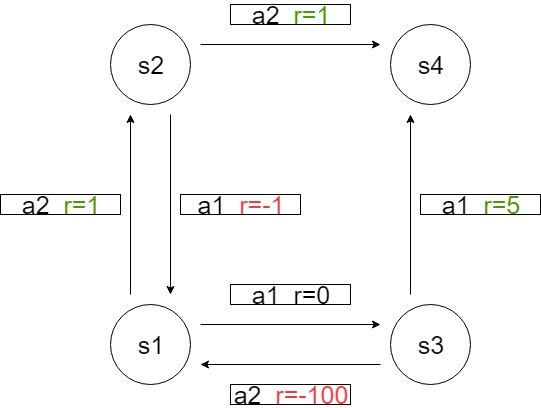
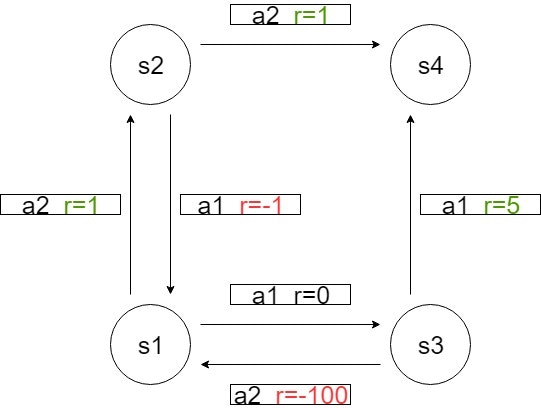
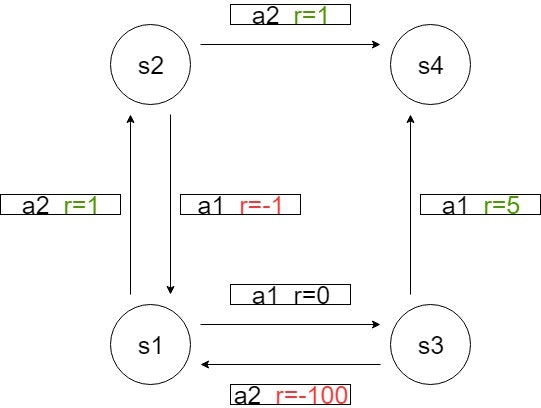
例えば次のような状態遷移図を考えてみましょう。
初期状態S=s1として、行動a2を取って状態S=s2に遷移したとします。
選択した方向に必ず進むなら、状態遷移確率P(s2|s1,a2)=1となり、r(s1,a2,s2)=1となります。
選択した方向に70%の確率ですすむなら、P(s2|s1,a2)=0.7となります。
良い方策とは何か?
エージェントが行動を決定するためのルールは方策とよばれπで表します。良い方策πを見つけるのが強化学習の目標となります。
行動したときの報酬の大きさを方策の指標にするのはどうでしょうか?
しかし、これはあまり適当ではありません。なぜなら、すぐには小さな報酬しか得られなくても、のちにとても大きな報酬を得ることができれば、はじめの行動は全体としてみればいい行動とみなせるからです。
そこで、現在の報酬から未来の報酬まで足し合わせた収益を考えます。
時間ステップtで得られた報酬をRtとして、区間Tにおける収益Gtは、

となります。
また、未来の不確実性を考慮して、報酬を割り引く形で表現する割引報酬和というのもあります。

収益Gtは区間Tの取り方によって確率的に変化するため指標としては使いづらいです。なので、収益の期待値を取った、状態価値関数を考え、良い方策πを定義するための指標にします。

Eπは方策πのもとでの期待値を表しています。
また、行動決定を行うためには、行動も条件に加えたほうが便利な場合が多いので、

これを行動価値関数と呼びます
価値反復に基づくアルゴリズム
ベルマン方程式
Eπは線形な演算なので、

また、方策πのもとで、状態sのとき、行動aが選択される確率をπ(a|s)と表すと(πは方策、π(a|s)は確率であることに注意)
第1項については、

となり、第2項については、

となります。このうち、

の部分は、Vπ(s')とみることができるので、第2項は、

となります。これらをまとめると、ある方策πのもとでの状態価値関数に関するベルマン方程式を得ます。

同様にして、行動価値関数についても、

よって、

となります。
さきほどの状態遷移図を使って、状態価値関数を計算してみましょう。
スタートはs1、ゴールはs4で、ゴールしたら終了です。
方策は行動a1のみを取る方策π1を考えます。

選択した方向に必ず進むとして、状態遷移確率P(s'|s,a)=1、割引率γ=0.8とします。
このとき、状態s1における状態価値関数は、

同様にして、

状態s4では報酬を得ることができないので、Vπ1(s4)=0

次に、行動a1とa2を等確率で選択する方策π2を考えます。

さきほどと同様にして、

すべての状態において、π1のもとでの状態価値のほうが高いので、π1はπ2よりも良い方策と定義することができます。
もし、状態によって状態価値の大小関係が変わる場合は、その二つの方策の間には優劣はつけないものとします。
SARSA
ベルマン方程式を使って状態価値を求めることができました。
しかし、上の例のように、ベルマン方程式から価値関数を求めるには状態遷移確率P(s'|s,a)がわかっている必要があります。
一般の強化学習ではそれは未知なので、状態遷移確率を直接使わずに価値関数を求めなければなりません。
エージェントが試行錯誤することで価値関数を求めるアルゴリズムとしてSARSAがあります。

←は左辺に右辺を代入して更新していくという意味です。状態遷移確率が未知の場合でも価値関数を計算することができます。
また、SARSAを式変形してみます。

Q(St,At)に第2項を加えていることがわかります。第2項のα以下の部分はTD誤差と呼ばれ、学習の収束からの離れ具合を表しています。もし、収束すればTD誤差は0になるはずです。
Pythonを使って実際にSARSAを実装してみましょう。
まずライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
次に状態遷移図の関数を実装
def StateTransition(s,a):
r=0
#状態s1
if s==S[0]:
#行動a1
if a==A[0]:
s=S[2]
r=0
#行動a2
if a==A[1]:
s=S[1]
r=1
#s2
elif s==S[1]:
#a1
if a==A[0]:
s=S[0]
r=-1
#a2
if a==A[1]:
s=S[3]
r=1
#s3
elif s==S[2]:
#a1
if a==A[0]:
s=S[3]
r=5
#a2
if a==A[1]:
s=S[0]
r=-100
return s,r
状態と行動を入力すると、報酬と次の状態を返します。
パラメータの設定と方策π、SARSAアルゴリズムの実装
学習率αは0.01、割引率γは0.8、試行回数(Episode)は3000です。
# とりうる状態と行動
S=np.array([0,1,2,3])
A=np.array([0,1])
# パラメータ
a1_per=0.5 #行動a1の選択確率
alpha=0.01
gamma=0.8
episode=3000
endEpi=False
# 価値関数の値を保存するためのリスト
Q=np.array([[10.,10.],[10.,10.],[10.,10.],[0.,0.]])
# グラフ表示のためのリスト
result_q_s1a1=[]
result_q_s1a2=[]
# 確率a1_perによって行動が決まる方策π
def Pi(a1_per):
#a1
if np.random.uniform(0,1) <= a1_per:
return 0
#a2
else:
return 1
# SARSAアルゴリズム
def SARSA(s,a,r,s_next,a_next):
#TD誤差
TD=r+gamma*Q[s_next,a_next]-Q[s,a]
#関数の更新
Q[s,a]+=alpha*TD
これらを使って、エージェントが試行錯誤しながらSARSAアルゴリズムで価値関数を更新していきます。Q(s1,a1),Q(s1,a2)の値をリストに保存し、最後にプロットします。
if __name__=='__main__':
for step in range(episode):
print('\n Step=', step+1)
#終了フラグ
endEpi=False
#初期状態
s=S[0]
a=Pi(a1_per)
#メインルーチン
while not endEpi:
#状態の遷移と報酬を得る
s_next,r=StateTransition(s,a)
#次の行動
a_next=Pi(a1_per)
#SARSA
SARSA(s,a,r,s_next,a_next)
#表示
print('\ns=', s, 'a=', a, 'r=', r,
's_next=', s_next, 'a_next=', a_next)
#更新
a=a_next
s=s_next
# s4に到達したら終了
if s == S[3]:
endEpi = True
# step毎のQの値を保存
#s1a1
result_q_s1a1.append(Q[0,0])
#s1a2
result_q_s1a2.append(Q[0,1])
#s1,a1
x=np.arange(0,episode,1)
y=result_q_s1a1
plt.plot(x,y,label='Q(s1,a1)')
#s1,a2
x=np.arange(0,episode,1)
y=result_q_s1a2
plt.plot(x,y,label='Q(s1,a2)')
#Q関数の値
print('\nQ=\n',Q)
#グラフの表示
plt.legend()
plt.ylim(-60,10)
plt.show()
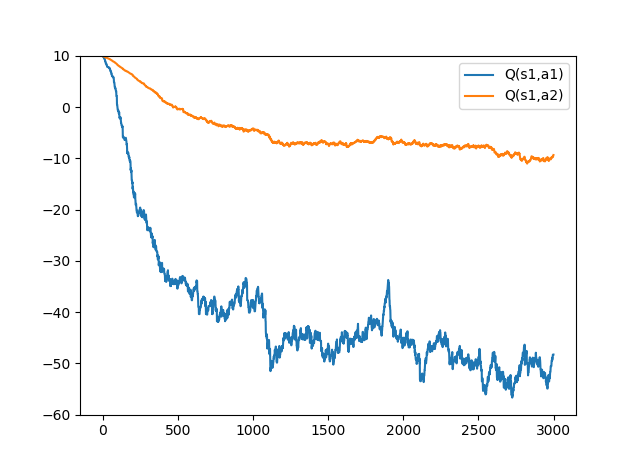
a1の選択確率が50%のとき(a1_per=0.5)
a1_per=0.5では行動がランダムなので、s3のときにr=-100になる場合が多く、Q(s1,a1)の値は低くなります。一方、Q(s1,a2)では失敗が少なく、より多くの報酬が得られることを学習しています。
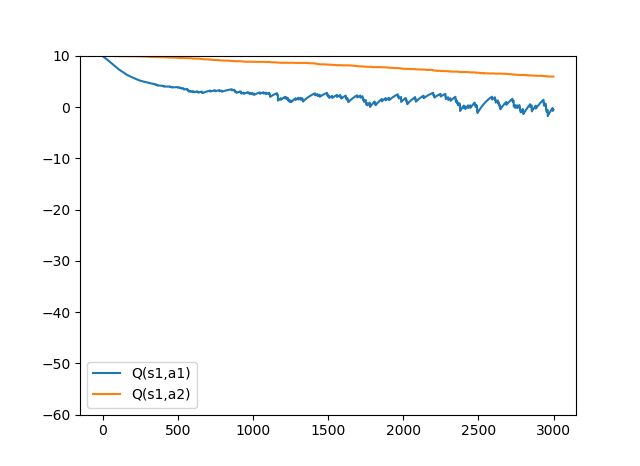
a1の選択確率が95%のとき(a1_per=0.95)
a1_per=0.5のときの方策に比べて、違う値に収束しました。
a1を選択する確率が95%なら、状態s3のときr=-100になる場合が低くなることが価値関数に反映されています。
Q-Learning
次にQ学習アルゴリズムについてご紹介します。

Q学習では常に最大の行動価値を目標値として更新していきます。
こちらもPythonで実装してみましょう。
# QLearning
def QLearning(s,a,r,s_next):
#TD誤差
TD=r+gamma*max(Q[s_next,0],Q[s_next,1])-Q[s,a]
#関数の更新
Q[s,a]+=alpha*TD
また、さきほどのメインルーチンのSARSAの部分を、
# =====省略=====
# 次の行動
a_next=Pi(a1_per)
#SARSA
SARSA(s,a,r,s_next,a_next)
#表示
print('\ns=', s, 'a=', a, 'r=', r,
's_next=', s_next, 'a_next=', a_next)
# =====省略=====
Q-Learningに差し替えます
# =====省略=====
# 次の行動
a_next=Pi(a1_per)
#Q-Learning
QLearning(s,a,r,s_next)
#表示
print('\ns=', s, 'a=', a, 'r=', r,
's_next=', s_next, 'a_next=', a_next)
# =====省略=====
グラフも見やすいようにy軸の範囲を変えます
plt.ylim(0,11)
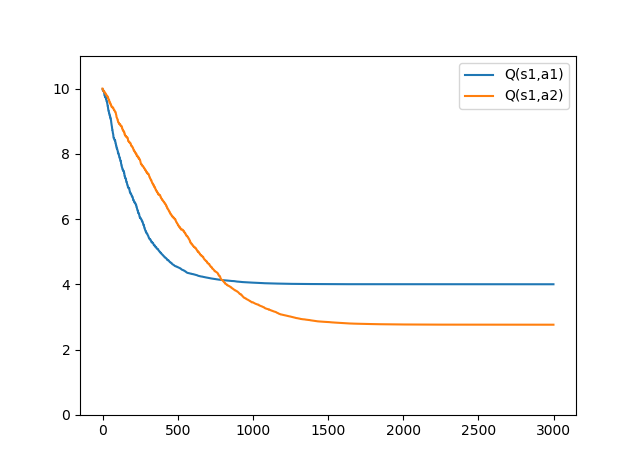
a1の選択確率が50%のとき(a1_per=0.5)
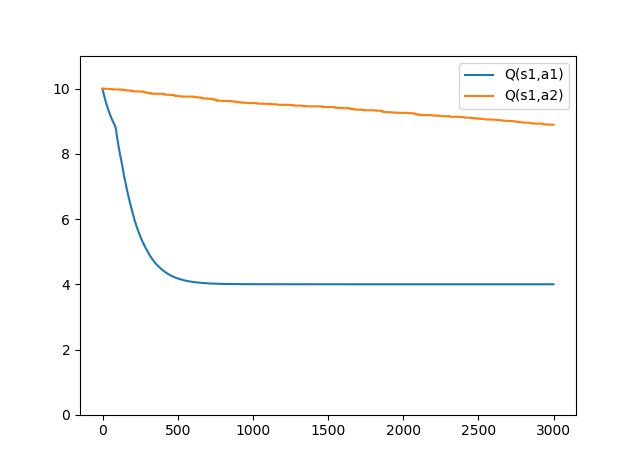
a1の選択確率が95%のとき(a1_per=0.95)
SARSAとは違う結果になりました。
これはQ-Learningは、エージェントがすべての場所で理想的な行動をした場合の価値を計算しているためです。なので、状態s3で行動a2をとる可能性を考慮していません。
Q-Learningで学習される最適行動価値関数は、方策によらず同じ値に収束します。
しかし、a1_per=0.95のように、あまり試されないような行動がある場合収束に時間がかかります。(a1_per=0.95のグラフはまだ収束していない)
価値反復法
a1_per=0.5, a1_per=0.95など方策πをあらかじめ決めていましたが、今度は価値反復法を使って、価値関数の更新に伴い方策πを決めていきたいと思います。
つまり、価値関数が大きくなるときの行動を選択していくということです。
しかし、常に最大値を選ぶようなgreedy法では局所解にハマる可能性があるので、確率εでランダム行動を行うε-greedy法を使います。
先ほどとパラメータは同じですが、さらに追加します。
tryNum=1000
# グラフ表示のためのリスト
resultQ_all_sum=[]
resultSARSA_all_sum=[]
価値反復法に基づくε-greedy法
# 価値反復法に基づく方策π
def Pi2(s_next):
#確率εでランダム行動
if np.random.uniform(0,1)<=epsilon:
a_next=np.random.choice([0,1])
#確率1-εで価値関数の最大値を選択
else:
a_next=np.argmax(Q[s_next])
return a_next
また、行動価値関数Qの部分、
# 価値関数の値を保存するためのリスト
Q=np.array([[10.,10.],[10.,10.],[10.,10.],[0.,0.]])
は削除し、メインルーチン内で初期化します。
if __name__=='__main__':
#QLearning
for i in range(tryNum):
print('QLearning {}/{} Completed'.format(i,tryNum))
# 価値関数を保存するためのリスト
#-1~1で初期化
Q=np.random.uniform(-1,1,(4,2))
for step in range(episode):
#報酬の合計
result_sum=0
# 終了フラグ
endEpi = False
# 初期状態
s = S[0]
a = Pi2(s)
# メインルーチン
while not endEpi:
# 状態の遷移と報酬を得る
s_next, r = StateTransition(s, a)
result_sum+=r
# 次の行動
a_next = Pi2(s_next)
# QLearning
QLearning(s, a, r, s_next)
# 更新
s = s_next
a = a_next
# s4に到達したら終了
if s == S[3]:
endEpi = True
#result_sumの保存
resultQ_all_sum.append(result_sum)
# 3000Episodeを1000回繰り返し平均収益を保存
# QLearning
#(1000,3000)にする
resultQ_all_sum = np.array(resultQ_all_sum).reshape((tryNum, episode))
#列に対して平均をとる
resultQ_all_sum_mean = np.mean(resultQ_all_sum, axis=0)
# プロット
x = np.arange(0, episode, 1)
y = resultQ_all_sum_mean
plt.plot(x, y, label='QLearning')
#SARSA
for i in range(tryNum):
print('SARSA {}/{} Completed'.format(i,tryNum))
# 価値関数を保存するためのリスト
#-1~1で初期化
Q=np.random.uniform(-1,1,(4,2))
for step in range(episode):
#報酬の合計
result_sum=0
# 終了フラグ
endEpi = False
# 初期状態
s = S[0]
a = Pi2(s)
# メインルーチン
while not endEpi:
# 状態の遷移と報酬を得る
s_next, r = StateTransition(s, a)
result_sum+=r
# 次の行動
a_next = Pi2(s_next)
# QLearning
SARSA(s,a,r,s_next,a_next)
# 更新
s = s_next
a = a_next
# s4に到達したら終了
if s == S[3]:
endEpi = True
#result_sumの保存
resultSARSA_all_sum.append(result_sum)
#SARSA
#(1000,3000)にする
resultSARSA_all_sum=np.array(resultSARSA_all_sum).reshape((tryNum,episode))
#列に対して平均をとる
resultSARSA_all_sum_mean=np.mean(resultSARSA_all_sum,axis=0)
#プロット
x=np.arange(0,episode,1)
y=resultSARSA_all_sum_mean
plt.plot(x,y,label='SARSA')
plt.ylim(-3,5)
plt.legend()
plt.show()
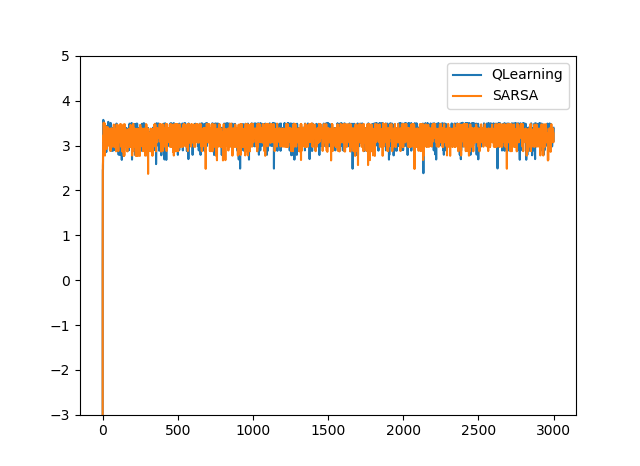
SARSA,Q-Learningをそれぞれ、3000エピソードを1000回繰り返し、その平均をグラフにプロットします。
ε=0.01のとき
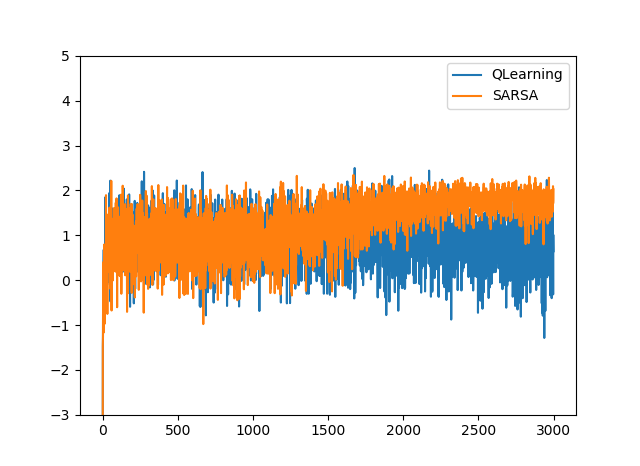
ε=0.1のとき
ε=0.01のときはどちらもほぼ同じ値に収束しました。
しかし、ε=0.1のときでは違う値に収束しています。これは、探索が多いため、Q-Learningでは状態s3のときにr=-100になる場合が多いことを表しています。
一方、SARSAでは探索によるノイズを含めた価値関数を学習しているため、探索が多い場合では、s1→s2→s4というルートを学習していることを表しています。
OpenAIGymのFrozenLake問題を解く
最後に応用として、より複雑なゲームで価値反復法によるQ学習を使ってみたいと思います。
ゲーム部分を実装するのは大変なので、OpenAIGymというものを利用します。
OpenAIGymでは強化学習をしやすいようにゲームを、Pythonでコマンド一発で使えるような形で提供されています。
pip install gym
で基本的に使えると思いますが、環境で多少変わるのでこちらの記事なども参照ください。
OpenAI Gym 入門
今回はFrozenLakeというゲームをやっていきます。

FrozenLakeでは左上のSからスタートし、右下のGに行けばゴールです。
状態は、左上のSからs=0,s=1,s=2...と続いていき、右下のGでs=15になります。
行動は、左(0)、下(1)、右(2)、上(3)
Fは凍った床で、Hが穴で落ちたら終了になります。
床が凍っているので、進みたい方向には1/3でしか進めず、残りの1/3ずつは左右にずれます。
import gym
import numpy as np
import matplotlib.pyplot as plt
# パラメータ
GAMMA=0.99
ALPHA=0.3
EPSILON=0.01
EPISODE=10000
STEP=100
CNT_GOAL=0
# 報酬の保存
result_mean=[]
# 価値関数
Q=np.random.uniform(-1,1,(16,4))
# 環境生成
env=gym.make('FrozenLake-v0')
# QLearning
def QLearning(s,a,r,s_next):
#TD誤差
TD=r+GAMMA*max(Q[s_next])-Q[s,a]
#関数の更新
Q[s,a]+=ALPHA*TD
# 価値反復法に基づく方策π
def ValueIteration(s_next):
#確率εでランダム行動
if np.random.uniform(0,1)<=EPSILON:
a_next=np.random.randint(0,4)
#確率1-εで価値関数の最大値を選択
else:
a_next=np.argmax(Q[s_next])
return a_next
if __name__=='__main__':
#価値反復法を用いて強化学習
for episode in range(EPISODE):
print('\n%d EPISODE\n' % (episode + 1))
# 環境リセット、初期状態取得
s = env.reset()
a = ValueIteration(s)
for t in range(STEP):
# 次の状態に遷移、報酬、終了条件を取得
s_next, r, done, _ = env.step(a)
# 報酬
if done:
# ゴールした時
if s_next == 15:
r = 2
CNT_GOAL += 1
# 穴に落ちたか、時間切れになったとき
else:
r = -1
# 次の行動
a_next = ValueIteration(s_next)
# 価値関数の更新
QLearning(s, a, r, s_next)
# 更新
s = s_next
a = a_next
# 終了条件に達したら終了
if done:
break
# 100EPISODEごとにゴールした回数の平均を記録する
if (episode + 1) % 100 == 0:
r_mean = CNT_GOAL / 100
result_mean.append(r_mean)
CNT_GOAL = 0
#最終的な価値関数を使って100回試行して表示してみる
for episode in range(100):
print('\n%d EPISODE\n' % (episode + 1))
# 環境リセット、初期状態取得
s = env.reset()
# ゲームの描写
env.render()
for t in range(STEP):
#行動
a=ValueIteration(s)
# 次の状態に遷移、報酬、終了条件を取得
s, _, done, _ = env.step(a)
#ゲームの描写
env.render()
# 終了条件に達したら終了
if done:
print('\n%dSTEP Finished' % (t + 1))
break
# 価値関数の表示
print('\n価値関数\n',Q)
# グラフ表示
x = np.arange(0, EPISODE / 100, 1)
y = result_mean
plt.plot(x, y)
plt.ylim(0, 1)
plt.show()
アルゴリズムや方策πの決定などは、上で説明したものと同じになります。
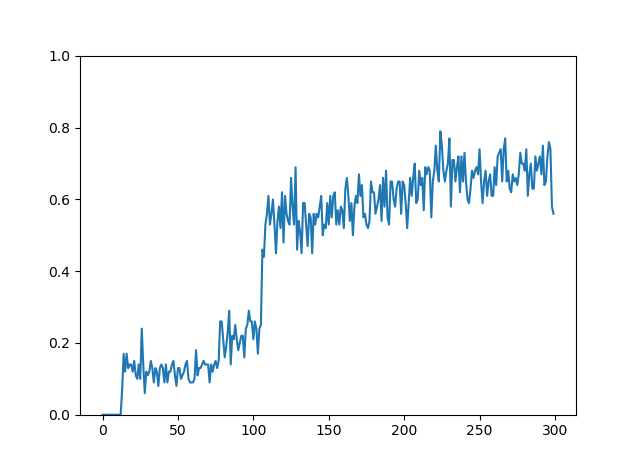
ゴールした回数を記録しておき、100エピソード毎に平均をとりグラフにプロットします。また、学習した行動価値関数を使って、100回ほど試しにゲームをして表示します。
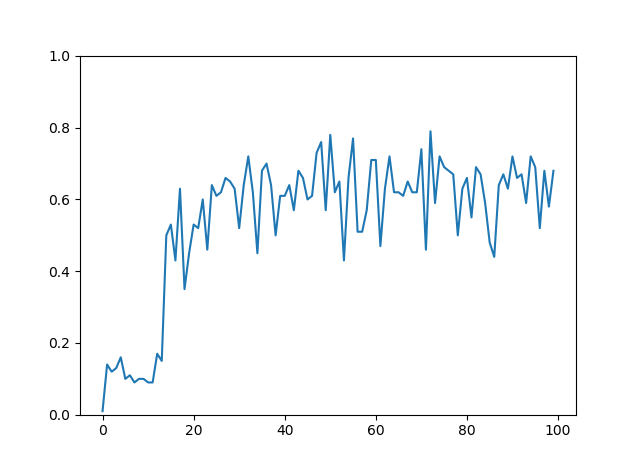
0.6前後に収束しました。これは確率60%前後でゴールしていることを意味します。(ただし、10000エピソードでは学習が収束しない場合もある)
行動価値関数の初期値によって学習の収束にかかる時間が変わります。

実際にみてみると、それなりの確率でゴールしていることがわかります。
学習率を変えてみる
学習率αは大きいと収束は早くなりますが安定しなくなります。逆にαを小さくすると、学習は安定しますが、収束に時間がかかります。
α=0.7
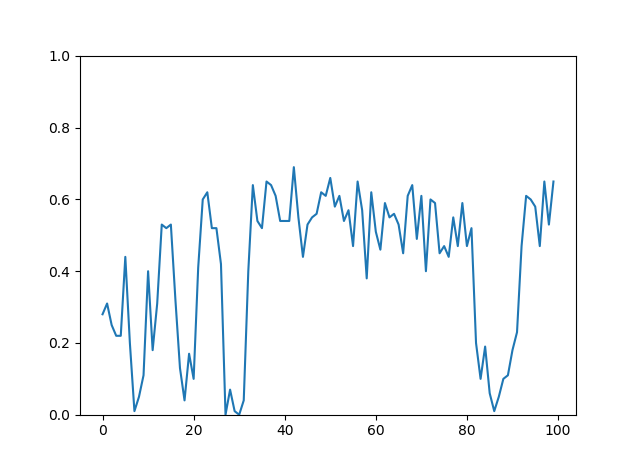
α=0.01
収束するまでに1万エピソード以上かかっている。