はじめに
前回はマルコフ連鎖とモンテカルロ法をそれぞれ解説し、マルコフ連鎖モンテカルロ法(通称:MCMC法)の概要をまとめました。
MCMC法は複数アルゴリズムがありますが、今回はメトロポリス・ヘイスティング方法(通称:MH法)をまとめたいと思います。
今回も下記記事及び、本を参考にして学びました。
マルコフ連鎖モンテカルロ法の振り返り
マルコフ連鎖モンテカルロ法(通称:MCMC法)は、多次元空間の確率分布等複雑な分布を確率分布に基づくサンプリングから求める方法です。
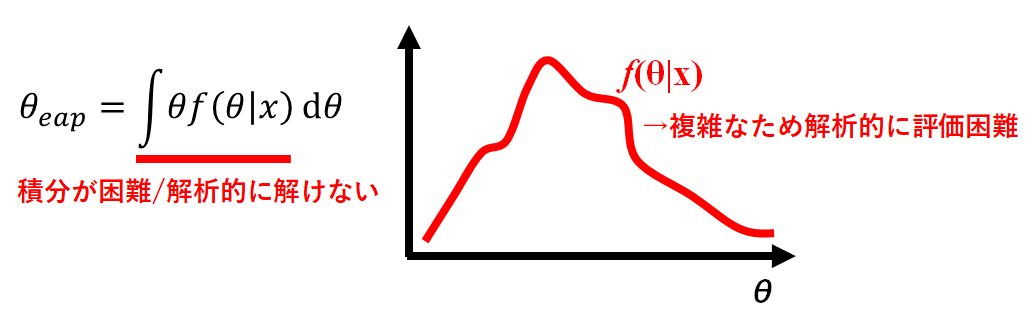
関数の期待値$θ_{eap}$を求めるうえで、データ分析を対象にすると高次元の関数になりがちです。その場合、計算が非常に複雑で解けない場合も多いため、その対象とする分布をランダムにサンプリング(モンテカルロ法)することを考えます。
そのサンプリングした値を集めた分布を所望の分布となるようマルコフ連鎖で調整していくのです。
このMCMC法は下記大きく4つの手法、アルゴリズムがあります。
- メトロポリス・ヘイスティング法(今回説明)
- ハミルトニアン・モンテカルロ法
- ギブズサンプリング
- スライスサンプリング
今回は、このメトロポリス・ヘイスティング法についてまとめます。
メトロポリス・ヘイスティング法とは
MCMC法では、任意の確率変数$θ,θ'$について下記に示す詳細釣り合い条件を考えます。
f(θ'|θ)f(θ) = f(θ|θ')f(θ') \hspace{1cm} 式1
この時、$f(θ'|θ)$及び$f(θ|θ')$が遷移核と呼ばれる分布です。通常、既知である事後分布$f(θ)$に対して式1を満たすような遷移核をいきなり見つけることは非常に困難です。
そこでこの遷移核$f(|)$の代わりに分析者が適当な遷移核$q(|)$を提案分布として利用します。この適当に選ぶことが実は難しさを表していることが後の実装で分かります。
提案分布とは、目標分布からのサンプルとして適当である候補を提案する確率分布です。この提案分布は適当に選ぶことから、必ずしも等号を満たすわけではありません。例えば、
q(θ|θ')f(θ') > q(θ'|θ)f(θ)\hspace{1cm} 式2\\
こちらの式2のようになります。この式について、詳細釣り合い条件として満たすために確率補正を行う方法を**メトロポリス・ヘイスティング(Metropolis-Hastings algorithm)法(通称MH法)**と呼びます。
元々は、物理化学の領域で提案されたアルゴリズムです。それをベイズ統計に応用されたのです。
式2は$θ$への移動確率が、$θ'$への移動確率よりも大きくなっている状態です。但し、遷移確率との補正を行うために、符号が正の補正係数$c$と$c'$を導入します。
f(θ|θ') = cq(θ|θ')\\
f(θ'|θ) = c'q(θ'|θ)
となるため、補正後は、
cq(θ|θ')f(θ')=c'q(θ'|θ)f(θ)
となって統合が成り立ちました。ただこの場合でも、
- 補正の係数が[tex:c,c']の二つあり冗長
- 補正係数が0以上1以下に収まっていないため、確率的行動をとりにくい
等の課題があります。従って、
r = \frac{c}{c'} = \frac{q(θ'|θ)f(θ)}{q(θ|θ')f(θ')}\\
r' =\frac{c'}{c'} = 1
となります。これを代入すると
rq(θ|θ')f(θ')=r'q(θ'|θ)f(θ)
となるため、$rq(θ|θ')$と$r'q(θ'|θ)$を遷移核とすれば、詳細釣り合い条件を満たすこととなります。
MHアルゴリズム
さて、MHアルゴリズムは下記です。
- 提案分布 $q( | θ^{t})$を利用して、乱数$a$を発生させる。
- 以下の命題を判定する。
q(a|θ^{t})f(θ^{t}) > q(θ^{t}|a)f(a)
- 真:式1 不等号条件より、$θ =a$,$θ' =θ^{t}$の状態と判定されます。この場合、提案分布は$q(θ|θ')$なので、式2の左辺の係数$r$を使って確率的補正をする必要があります。
r =\frac {q(θ^{t}|a)f(a) }{q(a|θ^{t})f(θ^{t})}
を計算し、確率$r$で$a$を受容し、$θ^{t+1}=a$とします。確率$1-r$で$a$を破棄し、$θ^{t+1}=θ^t$とします。
- 偽:式1 不等号条件より、$θ' =a$,$θ =θ^{t}$の状態と判定されます。この場合、提案分布は$q(θ'|θ)$なのですから、式2の右辺の係数$r'$を使って確率的補正をする必要があります。確率$1(=r')$で必ず$a$を受容し、$θ^{t+1}=a$とします。
3)$ t = t + 1$として、1へ戻る。
要約すると、提案された候補点$a$を確率$min(1,r)$で受容$(θ^{t+1}=a)$し、さもなくばその場に留まる$θ^{t+1}=θ^{t}$ことを任意回数繰り返すとなります。
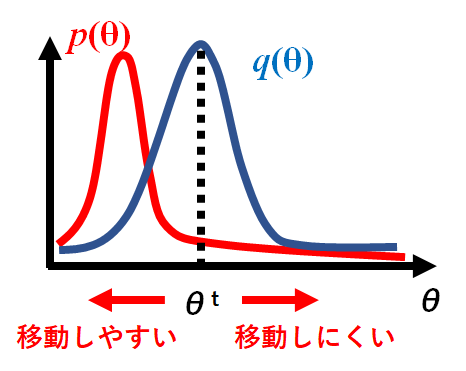
移動の概要を下記図としました。目標分布$f(θ)$に向かって$θ$は移動しやすい状態を作っています。
実装して確認する(独立MH法)
それでは実際にこのMH法を実装していきたいと思います。MH法には細かく独立MH法と、ランダムウォークMH法があります。まずは独立MH法についてです。
お題は下記です。
母数$θ$の事後分布を$f(θ|α=11, λ=13)$のガンマ分布と仮定する。そして、提案分布は平均1,分散0.5の正規分布$q(θ)$とする。
ここで、補正係数は
r =\frac {q(θ^{t})f(a) }{q(a)f(θ^{t})}
とする。プログラムは下記です(ライブラリのインポート等は書いておりません。後ほど全文リンクを御覧ください)。
theta = []
# Initial value
current = 3
theta.append(current)
n_itr = 100000
for i in range(n_itr):
# 提案分布からの乱数生成
a = rand_prop()
if a < 0:
theta.append(theta[-1])
continue
r = (q(current)*f_gamma(a)) / (q(a)*f_gamma(current))
assert r > 0
if r < 0:
#reject
theta.append(theta[-1])
continue
if r >= 1 or r > st.uniform.rvs():#乱数を発生させて、rよりも大きい場合に受容させる
# Accept
theta.append(a)
current = a
else:
#Reject
theta.append(theta[-1])
ポイントとしては、確率$r$で受容するかどうかを決める表し方です。
if r >= 1 or r > st.uniform.rvs()
st.uniform.rvs()メソッドにより$0~1$の一様分布における乱数を発生させてやり、それより大きいと受容させると決めています。
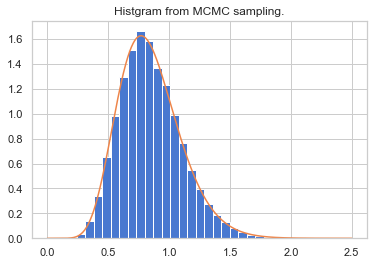
このプログラムの結果、事後分布を再現できているか確認します。
plt.title("Histgram from MCMC sampling.")
plt.hist(theta[n_burn_in:], bins=30, normed=True)
xx = np.linspace(0, 2.5,501)
plt.plot(xx, st.gamma(11, 0, 1/13.).pdf(xx))
plt.show()
ヒストグラムとして青で表しているデータがMH法により移動した$θ$の頻度分布です。正規化して和が1となるように補正しています。
オレンジ色が元々再現したかった事後分布ですので、再現できていることが確認できます。
さて、問題なくできたように見えますが先ほど提案分布では平均1、分散0.5としました。これは恣意的であり、実は上手くいかない場合があります。
例えば、平均を3、分散を0.5の正規分布が提案分布とすると、
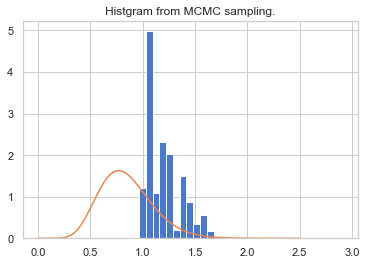
このようにずれてしまいます。実は、独立MH法においては目標分布に近い分布を定常分布としないと上手く収束してくれない課題があります。つまり、独立MH法は提案分布の良し悪しによって、収束までの成績に大きな違いが現れます。
今回は、簡単のために事後分布が明らかになっていますが、実際のデータ解析では分布が不明場合が多くあります。
従い、この課題を解決する方法を考える必要があります。
ランダムウォークMH法
この課題を解決する方法として、ランダムウォークMH法呼ばれるアルゴリズムが提案されています。
提案の候補を
a =θ^{t} + e
とします。$e$は平均0の正規分布や一様分布などが用いられます。
提案分布に正規分布や一様分布などの対称な分布を選ぶと、
q(a|θ^{t}) = q(θ^{t}|a)
と提案分布がかけます。
従い、ランダムウォークMH法における補正係数rは、
r = \frac {f(a)}{f(θ^{t})}
となり、提案分布が常に消えます。
実装して確認する(ランダムウォークMH法)
さて、先ほどと同じ問題について実装して確認してみましょう。
# MCMC sampling
theta = []
current = 5
theta.append(current)
n_itr = 100000
prop_m = 5
prop_sd = np.sqrt(0.10)
x = np.linspace(-1,5,501)
def rand_prop1(prop_m):
return st.norm.rvs(prop_m, prop_sd)
for i in range(n_itr):
a = rand_prop1(current) # 提案分布からの乱数生成
r = f_gamma(a) / f_gamma(current)
if a < 0 or r < 0:
#reject
theta.append(theta[-1])
pass
elif r >= 1 or r > st.uniform.rvs():
# Accept
theta.append(a)
current = a
status = "acc"
col = "r"
else:
#Reject
theta.append(theta[-1])
pass
グラフ描写が下記です。
plt.title("Histgram from MCMC sampling.")
n, b, p = plt.hist(theta[n_burn_in:], bins=50, density=True)
xx = np.linspace(0, 2.5,501)
plt.plot(xx, st.gamma(11, 0, 1/13.).pdf(xx))
plt.show()
kk = 11.
tt = 13.
print ("sample mean:{0:.5f}, sample std:{1:.5f}".format(np.mean(theta), np.std(theta)))
# 理論期待値・分散
print("mean:{0:.5f}, std:{1:.5f}".format( kk/tt, np.sqrt(kk*((1/tt)**2))) )
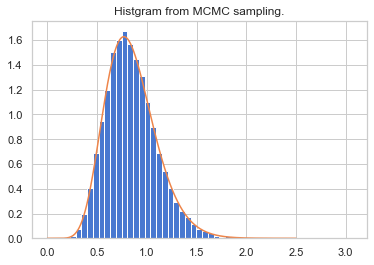
きれいに分布が再現できていることが分かりました。
先ほどの独立MH法と比較しても、こちらのランダムウォークMH法のアルゴリズムが安心して使えそうであることが分かりました。
と言いつつもMH法の問題点
これで一安心、と言いたいところですが実はまだまだ課題が残っています。結局、$e$の値を適切に指定する必要であるため、これもハイパーパラメータ的な考え方が必要になっています。
分散が小さければ受理される遷移の割合は高いものの、状態空間での前進はゆっくりとしたランダムウォークであるため、長い収束時間が必要になります。一方、分散が多きければ棄却率が高くなります。
これを解決する方法にハミルトニアンモンテカルロ法があります。それについては次回まとめられればと思います。
終わりに
今回、メトロポリス・ヘイスティング法をまとめました。事後分布の平均に向かって収束させていく方法を考えることは、さながらニューラルネットワークにおける重みパラメータの最適化に似ています。
結局アルゴリズムは異なるものの、行いたい目的は似ているのでそこが掴めると統計・機械学習の面白さや広がりが見えてくるように思いました。
プログラム全文はこちらに格納しております。
https://github.com/Fumio-eisan/Montecarlo20200516