はじめに
現在、ベイズ統計について学んでいます。その中から、マルコフ連鎖モンテカルロ法についてまとめます。本記事では入り口として、マルコフ連鎖やモンテカルロ法の概要について説明します。
今回参考にさせて頂いた本はこちらです。
マルコフ連鎖モンテカルロ法とは何か
ベイズ推論において、観測データを$X$、パラメータや潜在変数などの非観測の変数をまとめた集合を$Z$としたとき、確率モデル$P(X,Z)$を考えます。このとき、学習や予測といった具体的な課題を解決するためには$P(Z|X)$の事後分布を計算することが必要です。
さて、この事後分布は解析的に解くことができなかったり、数値的に解くことが非常に計算量が多くなる課題があります。
そこで、この求めたい分布の特性を$P(Z|X)$から複数のサンプルを得ることによって調べようとします。このサンプルリング方法として、マルコフ連鎖モンテカルロ法があるのです。
それぞれの用語を簡単に説明すると、
- マルコフ連鎖:次の状態は、前の状態からのみで決まる
- モンテカルロ法:乱数を用いた試行で近似解を求める手法
となります。下記で簡単にそれぞれまとめます。
モンテカルロ法(Monte Carlo Methods)
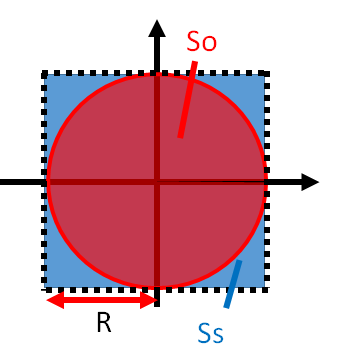
乱数を用いた試行で近似解を求める手法です。よく説明の例に用いる内容として、円周率$π$の近似解があります。これは、半径$R$の円及びそれを覆う正方形を考えます。
このとき、円の面積を$So$、正方形の面積から円の面積を引いた面積を$Ss$とすると、
So = πR^2\\
Ss = 4R^2-πR^2\\
と表すことができます。
さて、この二つの式を足して$π$を$So$と$Ss$を用いて表します。
π = \frac {4So}{So + Ss}
となります。
ここで、半径を$1$に直して考えます。
区間$[0,1]$において乱数を生成することで円内に入った場合は$1$、円外の場合は$0$として$1$となる確率を求めます。
例としてpythonで実装します。
import random
inner =0
for i in range(1000000):
x, y = random.random(), random.random()
if x**2 + y**2 < 1:
inner +=1
print (inner * 4/1000000)
$3.141072$となりました。凡そ$3.1415$に近い値となることが分かりました。乱数によって近似を行うモンテカルロ法を確認しました。
マルコフ連鎖(Markov Chain)
マルコフ連鎖とは、一個前の状態だけによって次の状態が決まることを指します。高校数学で習う漸化式をご存じの方は、それを思い浮かべて頂けると良いかと思います。
実際の例で一個前の状態から決まる事象は思い浮かべにくいのですが、教科書やウェブページで見た例がこちらです。
- 天気の例:明日の天気が、今日の天気のみで決まると仮定
- 服装の例:明日着る制服の種類が、今日の制服の種類のみで決まると仮定
- お弁当の例:明日食べるお弁当の種類が、今日食べるお弁当の種類のみで決まると仮定
等々上げだしたらきりがありません。
ここで、例題を考えます。
ネクタイ問題:ある高校では、制服のネクタイが公式に3種類用意されています。朱、緑、青です。一年生は100人いるとします。第一日目は朱、緑、青のネクタイをそれぞれ、$0.6,0.25,0.15$の確率で着用して登校することが経験的に知られています。この高校の生徒は、前日に絞めたネクタイ柄にだけ基づいて当日のネクタイ柄を決めます。
その確率下記に示します。さて、1日後、あるいは10日経過したときにそれぞれの色を着用している確率はどうなるでしょうか。
|表|当日:朱 |当日:緑 |当日:青|
|:---:|---|---|---|---:|
|前日:朱|0.3|0.3|0.4
|前日:緑|0.1|0.5|0.4
|前日:青|0.2|0.6|0.2
第$t$日のネクタイの柄を表す確率変数を、添え字$t(=1,....,T)$を用いて$X^{t}$とします。時間と共に変化する確率変数を確率過程と呼びます。一般的な確率過程は、
P(X^t|X^{t-1},・・・,X^1)
のように、それ以前の経緯を踏まえた条件付き確率になります。
しかしながら今回の場合では、
P(X^t|X^{t-1},・・・,X^1) = P(X^t|X^{t-1})
のように、前日の確率にのみ影響を受ける確率過程を、マルコフ連鎖と呼ぶのです。
このマルコフ連鎖を規定する条件付き確率を下記のように表すことができます。これを遷移核(transition kernel)あるいは推移核と呼びます。
{\bf{P}}=\begin{pmatrix} 0.3 & 0.3 & 0.4 \\
0.1 & 0.5 & 0.4 \\
0.2 & 0.6 & 0.2 \end{pmatrix}
定常分布への収束
さて、何日間か経った後の確率分布を求めようと思います。$p_朱^{t} = p(X^{t} = 朱)$と表記すると、$X^{t}$の確率分布は$\textbf p^{t} =(p_1^{t},p_2^{t},p_3^{t})$であり、$\textbf p^{1} =(0.6,0.25,0.15)$となります。
2日目に朱のネクタイを着用する確率は、
$\textbf p(X^2 = 朱) =0.3×0.6 + 0.1×0.25 + 0.2×0.15 = 0.235$
となります。
同じような考え方で繰り返し計算すると以下のように求めることができます。
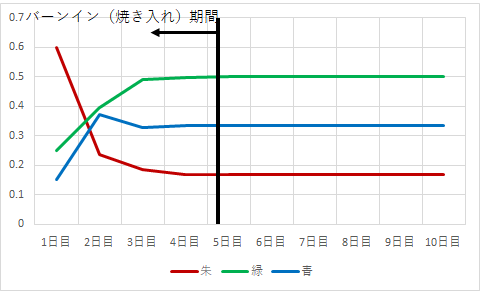
凡そ、4日目以降は変化が無くなっていることが分かります。先ほどの答えとしては、「4日目以降は朱:緑:青 =1/6:1/2 : 1/3で安定する」となります。
このとき変化しなくなった確率分布$\bf p$を定常分布あるいは不変分布と呼びます。また、この定常分布に代わるまでの間をバーンイン期間と呼びます。
詳細釣り合い条件(マルコフ連鎖・モンテカルロ法の融合)
このネクタイ問題では、最終的な着用状態である定常状態を求めることが目的でした。しかし、今回は事後分布が明らかな状態で、事後分布に合う乱数を手に入れたいと考えます。
換言すると、事後分布が定常分布になるような遷移核を設計することを考えます。
このように、サンプルリングしたい分布に対して、それを定常分布とするマルコフ連鎖を構成する方法をマルコフ連鎖モンテカルロ法(通称:MCMC法)と呼ぶのです。
MCMC法では、定常分布が既知であるものの、遷移核が未知です(ネクタイ問題と逆)。
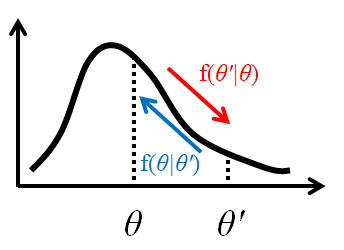
ここでマルコフ連鎖が定常分布に収束するための条件として、詳細釣り合い条件という考え方を用います。確率変数$θ,θ'$について、下記式のことを指します。
f(θ'|θ)f(θ) = f(θ|θ')f(θ')
先ほどのネクタイ問題の場合だと、
p(朱|緑) ×\frac {1}{6} = p(緑|朱) ×\frac {1}{2}
となります。
$f(θ'|θ)$や$f(θ|θ')$が遷移核となります。
こちらに詳細釣り合い条件の概要を示します。点$θ$を分布の中心付近とし、点$θ'$を分布の周辺部とします。このとき、詳細釣り合い条件が意味するところは、
f(θ'):f(θ) = 1 :a ならば\\
f(θ|θ'):f(θ'|θ) = a :1
となります。
$θ'$→$θ$の移動は$θ$→$θ'$の移動より$a$倍起こりやすいことを言います。つまり、中心付近に移動しやすいことを表しています。
この詳細釣り合い条件が見た割れていれば、初期状態をでたらめに取っていてもいずれ中心部に乱数列が引き寄せられることを意味します。
終わりに
マルコフ連鎖とモンテカルロ法をそれぞれまとめた後、マルコフ連鎖モンテカルロ法としてネクタイ問題を例にまとめました。
概要がまとまりましたので、次回このMCMC法を活用するアルゴリズムの説明を取り扱いたいと思います。
次の記事です。
メトロポリタン・ヘイスティング法(マルコフ連鎖モンテカルロ法における手法の一つ)を実装を交えて理解する
https://qiita.com/Fumio-eisan/items/6e8bad9977e945ddb2fc
ブログとしても下記記載いたしました。さらに詳しくまとめていく役割としています。