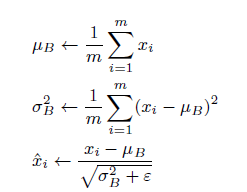はじめに
GAN:敵対的生成ネットワーク関連の内容です。GANにおけるモデルは必ずしも訓練によって本物と見分けがつかない画像に収斂していくわけではありません。
訓練が進まない理由として、勾配の消失・モード崩壊という不安定性があります。
この不安定性は、Discriminator(識別器)のリプシッツ連続やリプシッツ定数のコントロールが重要だと言われています。この不安定性を解消するには、Spectral Normalizationが便利です。
さて、、、分からない言葉がいくつか出てきました。今回はこれらの意味するところを私なりに解釈した内容をまとめたいと思います。
今回も参考にさせて頂いた本はこちらです。
Inpaintingからディープラーニング、最新のGAN事情について学べる本を書いた
https://qiita.com/koshian2/items/aefbe4b26a7a235b5a5e
- リプシッツ連続、リプシッツ関数とは
- 特異値分解とは
- Spectral Normalizationとは
リプシッツ連続、リプシッツ関数とは
関数$f(x)$がリプシッツ連続であるとは、任意の$x_1$,$x_2$に対して、
|\frac{f(x_1)-f(x_2)}{x_1-x_2}| \leq k 式1
を満たすような定数$k$が存在することを言います。この$k$はリプシッツ定数と呼びます。
さて、リプシッツ連続の内容を進める前に、関数が連続であることを振り返りたいと思います。
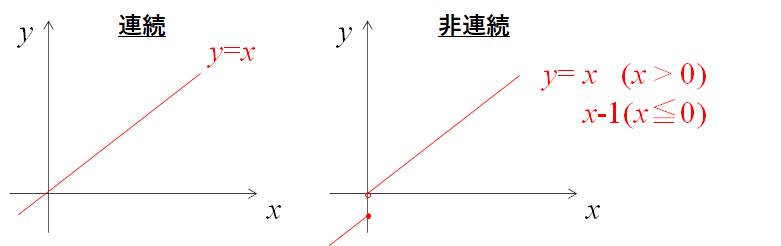
単に、関数が連続だという場合は下記です。
$x=x_0$で連続とは、
\lim_{x \to x_0} f(x) = f(x_0) 式2\\
が成立することをいいます。そして、対象とするすべての点で連続であるときに、$f(x)$は連続関数であるといえます。
例えば下記のような例が連続関数と連続関数で無い場合をいいます。
直感的に理解しやすいかと思います。
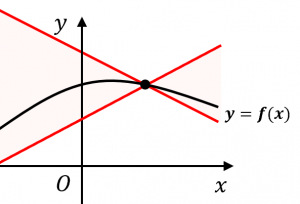
一方、リプシッツ連続とは、上記の式1を満たす$k$が存在する関数となります。
上の図において、関数上のどの点でも傾き $±k$ の直線を引くと、関数のグラフはその間におさまっている状態をリプシッツ連続であると呼びます。
先ほどの$y=x$を例に考えてみましょう。式1は、
|\frac{f(x_1)-f(x_2)}{x_1-x_2}| \leq k \\
\Rightarrow 1\leq k
となります。従って、$k$の値が0.01などの場合は式が成り立たなくなるので、この関数はリプシッツ連続であるといえなくなってしまいます。
従って、 関数が連続であることと、リプシッツ連続であることは
リプシッツ連続\in連続
にように連続が包含する形になります。
GANでは通常$k=1$と制約をおくことが安定性を高めるとされている経験則になります。
参考URL
https://mathwords.net/lipschitz
特異値分解とは
次に特異値分解(singular value decomposition)について説明します。この特異値分解とは行列における操作のことで、下記のSpectral Normalizationにとって必要な操作となるため、ここでまとめます。
特異値分解とは、任意の$m×n$行列$A$に対して、$A = UΣV$となる直行行列$U,V$及び非対角成分が0、対角成分が非負で大きさの順に並んだ行列$Σ$で分けることを言います。
そして、この$Σ$の成分を特異値と呼びます。
$U,V,Σ$の求め方に関しては下記pdfを参照頂ければと思います。
さて、Pythonではこれら特異値分解は簡単に求めることができます。
import numpy as np
data = np.array([[1,2,3,4],[3,4,5,6]])
U, S, V = np.linalg.svd(data)
print(U)
print(S)
print(V)
[[-0.50566621 -0.86272921]
[-0.86272921 0.50566621]]
[10.73807223 0.8329495 ] #特異値
[[-0.28812004 -0.41555404 -0.54298803 -0.67042202]
[ 0.7854851 0.35681206 -0.07186099 -0.50053403]
[-0.40008743 0.25463292 0.69099646 -0.54554195]
[-0.37407225 0.79697056 -0.47172438 0.04882607]]
このようにして、特異値は[10.73807223 0.8329495 ]であることが確かめられました。最大特異値は10.74程度であることが分かります。
参考URL
https://thinkit.co.jp/article/16884
Spectral Normalizationとは
さて、最後のこのSpectral Normalizationについてです。ニューラルネットワークの層を作りこむ上ではBatch Normalization(以下Batch Norm)と呼ばれる手法が有名です。
このBatch Normは、2015年に提案された手法です。全結合層や畳み込み層の後に組み込まれる層になっています。効果としては以下です。
- 学習が早く進行(=損失関数の値が収束しやすい)
- 初期値に依存しにくい(ロバスト性がある)
- 過学習の抑制
処理としては以下のような処理を行います。
ミニバッチとして$x_1,x_2・・・x_m$の$m$この入力データに対して、平均$μB$,分散$σ_B^2$を求めています。
これら効果を享受できるBatch Normですが、ことGANの学習に関しては連続性を損なる要因として挙げられています。
上記式でもわかるように、Batch Normは標準偏差で割っているため分数関数の表現になります。分数関数は、$x=0$で連続で無いことから連続性を損なっていることが理解できます。
従って、この問題を解決する手段がSpectral Normalizationになります。
Spectral Normalization for Generative Adversarial Networks
https://arxiv.org/abs/1802.05957
これは日本人が著者で、株式会社Preferred Networksの方々が発表したものです。
Spectral Normalizationは係数を最大特異値で割るという考えになります。モデルに対して、リプシッツ連続性を担保し、リプシッツ定数が1となるようにコントロールすることができます。
この最大特異値を求めるために、先の特異値分解を用います。
実装上は非常に簡便です。tensorflowを用いた場合は解のようにConvSN2Dにより規定することで実装できます。
import tensorflow as tf
from inpainting_layers import ConvSN2D
inputs = tf.random.normal((16, 256, 256, 3))
x = ConvSN2D(64,3,padding='same')(inputs)
print(x.shape)
さて、この特異値を求める方法ですが、そのままsvdメソッドを適用すると計算量が膨大になるため、べき乗法というアルゴリズムを用います。
$(N,M)$の行列$X$における最大特異値は
- $U:(1,X)$の行列$U$を定義する。そのとき正規乱数として初期化
- 以下をP回繰り返す
- $V=L_2(UX^T)$を試算。ただし$L2=x/\sqrt(Σx_{i,j})+ε$ ,($ε$は微小量)
- $U=L_2(VX)$を試算。
- $σ = VXT^T$を試算。$σ$が最大特異値となる。
実装すると下記になります。元のdata行列は上で用いたものです。
results = []
for p in range(1, 6):
U = np.random.randn(1, data.shape[1])
for i in range(p):
V = l2_normalize(np.dot(U, data.T))
U = l2_normalize(np.dot(V, data))
sigma = np.dot(np.dot(V, data), U.T)
results.append(sigma.flatten())
plt.plot(np.arange(1, 6), results)
plt.ylim([10, 11])
さて、10.74あたりで先ほどと同じ結果が得られました。このようにして実装上は求めています。
終わりに
今回、Spectral Normalizationに関わる内容をまとめました。大枠な流れはつかんだものの、数学的なところに関しては理解不足なことが残りました。
引き続き実装を行う中で理解を深めたいと思います。
プログラムはこちらに格納しています。
https://github.com/Fumio-eisan/SN_20200404