多層ニューラルネットワーク(Keras)のパラメータを変えて損失関数の値に与える影響を評価した（題材：MNIST分類）

はじめに

　
　ニューラルネットワークはKerasやChainer, Torchなど多くのフレームワークが用意されており1行ずつ組み合わせることで簡単にモデルを作成することが可能です。
　なるべく早い時間で計算を行え、正確であることが良いモデルです。
　今回、正確なモデルを作成する観点でモデルのパラメータを変えたときに損失関数の値に与える影響を評価しました。

　
　今回の要点はこちらです。

• モデルの概要
• 活性化関数による差
• 最適化手法による差
• ニューラルネットワークの層による差

モデルの概要

　今回はチュートリアルとしてよく使用される手書き数字認識MNISTを題材にします。ニューラルネットワークはKerasのフレームワークを用いて構成したいと思います。
　Kerasの場合は以下の記述でニューラルネットワークモジュールをインポートすることが可能で、かつMNISTデータを格納させることが可能です。

NN.ipynb

import tensorflow as tf
import tensorflow.keras.layers as layers
from tensorflow.keras.layers import LeakyReLU
from sklearn.model_selection import train_test_split
(X_train,y_train),(X_test,y_test)=tf.keras.datasets.mnist.load_data()

　ちなみに使用したkeras及びtensorflowのバージョンは下記です。tensorflow下のkerasとして動かしています。

• tensorflow 2.1.0
• keras-applications 1.0.8
  
• keras-preprocessing 1.1.0

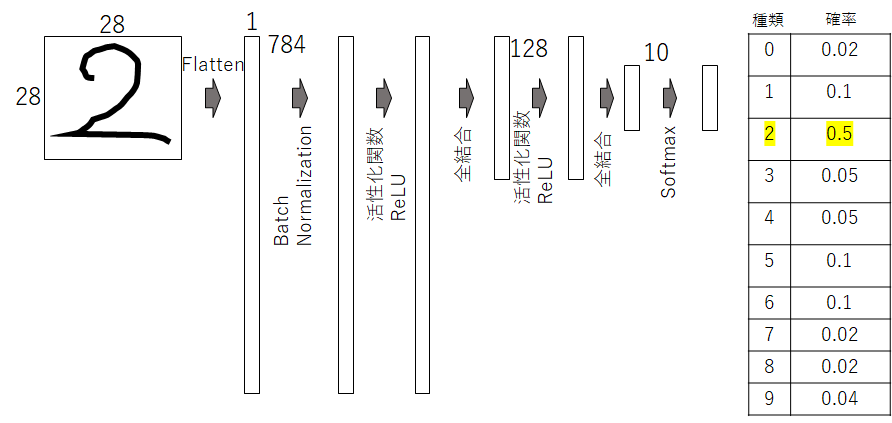
　ニューラルネットワークのモデルの構成はこちらです。今回は畳み込みを利用せずに最初に平坦化させています。そして、全結合層は2層あります。

NN.ipynb

inputs = layers.Input((28,28))　# 入力層
x = layers.Flatten()(inputs)　# 平坦化
x = layers.BatchNormalization()(x)　# Batch Normalization（収束させやすくします）
x = layers.Dense(128, activation='relu')(x)　#全結合層
x = layers.Dense(10, activation="softmax")(x)　#全結合層&ソフトマックス関数
outputs = x
model = tf.keras.models.Model(inputs, outputs)

kerasにはモデルの概要を見えることができるコマンドsummaryが用意されています。

NN.ipynb

model.summary()

Model: "model_10"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_11 (InputLayer)        [(None, 28, 28)]          0         
_________________________________________________________________
flatten_10 (Flatten)         (None, 784)               0         
_________________________________________________________________
batch_normalization_9 (Batch (None, 784)               3136      
_________________________________________________________________
dense_21 (Dense)             (None, 128)               100480    
_________________________________________________________________
dense_22 (Dense)             (None, 10)                1290      
=================================================================
Total params: 104,906
Trainable params: 103,338
Non-trainable params: 1,568

　各層での処理やパラメータなどよく分かりますね。

活性化関数による差

　まずは活性化関数の差による損失関数の収束の仕方を評価していきたいと思います。今回は代表的なものとして下記４つを試します。

• ReLU
• LeakyReLU
• tanh
• Sigmoid

　各関数の概要は多くのページで解説されています。私もまとめたものがありますので、こちらをご覧頂けると幸甚です。

3層順伝搬型ニューラルネットワークを自作して、計算を深く理解しようとした
https://qiita.com/Fumio-eisan/items/3038041c1ed076d643e7

モデルの定義

NN(acti.)OK.ipynb

inputs = layers.Input((28,28))
x = layers.Flatten()(inputs)
x = layers.BatchNormalization()(x)
x = layers.Dense(128, activation=LeakyReLU(alpha=0.01))(x)#ここを書き換えて活性化関数を変更
x = layers.Dense(10, activation="softmax")(x)
outputs = x
model = tf.keras.models.Model(inputs, outputs)

さて、上記の一文を変えることで活性化関数を変えることができます。

モデルのコンパイルと学習

NN(acti.)OK.ipynb

model.compile('adam', 'sparse_categorical_crossentropy',['sparse_categorical_crossentropy'])
history = model.fit(X_train, y_train, epochs=10, verbose=1, validation_data=(X_test, y_test))

NN(acti.)OK.ipynb

nb_epoch = len(loss1)
plt.plot(range(nb_epoch), loss1, label='ReLU')
plt.plot(range(nb_epoch), loss2, label='sigmoid')
plt.plot(range(nb_epoch), loss3, label='tanh')
plt.plot(range(nb_epoch), loss4, label='LeakyReLU')
plt.legend(loc='best', fontsize=10)
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

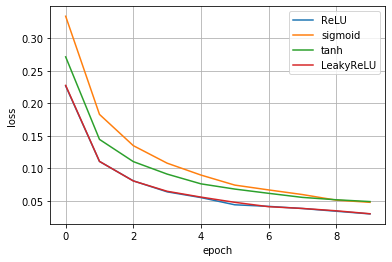
この縦軸のloss値（＝損失関数の値）が低くなるほどより誤差が少ない正確なモデルであることを意味します。
結果は、ReLUとLeakyReLUが同等でその次にtanh<sigmoidであることが分かりました。基本、ReLUを使っていることが多い理由が分かりましたね。

最適化手法による差

続いて、最適化手法の差です。最適化手法は損失関数の値を小さくするうえで、重みパラメータなどの値を更新する方法です。詳細はこちらの記事をご覧ください。

ニューラルネットワークにおける最適化手法（ＳＧＤからＡＤＡＭまで）を丁寧に理解しようとした
https://qiita.com/Fumio-eisan/items/798351e4915e4ba396c2

最適化手法は下記のコンパイル時に引数として与えることで指定することができます。
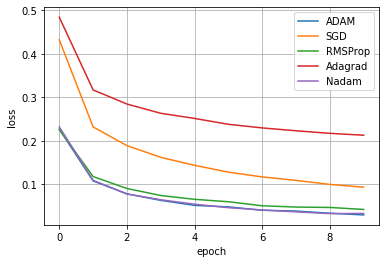
今回適用した最適化手法は歴史順にSGD,RMSProp,Adagrad,Adam,Nadamです。

NN(opti.)OK.ipynb

model.compile('adam', 'sparse_categorical_crossentropy',['sparse_categorical_crossentropy'])

※下記は活性化関数はReLUに統一です。

結果がこちらになります。やはり、AdamとNadamが良いことが分かります。RMSpropもかなり良いloss値まで下がっています。多くのモデルでAdamを推奨していることが分かりますね。

ニューラルネットワークの層による差

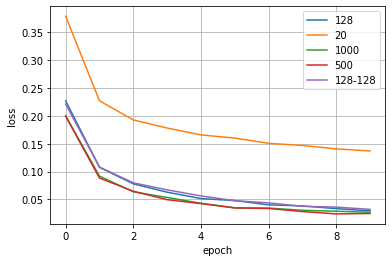
　最後に、ニューラルネットワークの層の決め方による差を評価します。下記に示す条件を試算しました。

※活性化関数はReLU(活と表記）, 最適化手法はAdam, BatchNormalizationはBNと表記しています。

　その結果がこちらです。だいたい一緒なのですが、中間層が20のCase3.の収束が遅いことが分かります。あまりに中間層の数が少ないと区別する表現が乏しくなるためだと思います。逆に、それ以上の１２８以上だとほぼサチレートしていくことから、これ以上の表現力では今回のMNISTでは十分であることが分かります。

終わりに

今回、地道に条件を変えてニューラルネットワークの損失関数の値を評価しました。活性化関数はReLU、最適化手法はADAMと一般的に使われている手法に行きついている理由がよくわかりました。

　次回は畳み込みの最適化に着目した評価をしていければと思います。

プログラムはこちらに格納しています。
※パラメータを変えることはご自身でお願いいたします。そのまま動かすと一条件のみの結果が出力されるプログラムになっています。
https://github.com/Fumio-eisan/minist_mlp20200307