はじめに+雑感(機械学習/深層学習の技術進歩って早いですね)
製造業で非システム部門で働く私にとって、ニューラルネットワークを初めとする機械学習周りの技術(≒アルゴリズム?)進歩はものすごく早いものだと感じます。日々新しいアルゴリズムが開発され、arXivといった審査がほぼ無い論文サイトに公開されます。そして、github等のプラットフォームによりすぐに(ある程度)誰でも実装することができることは、ものづくり産業である製造業と技術の進歩が全く異なります。
私の業界で新しい装置や技術が開発されたとなれば、まずはそれを導入することで得られるメリットを見積もる必要があります。そして装置を導入する投資額に対して、得られるメリットが見合えば、稟議書を通して予算をつけてもらい、購入に移ることができます。この時点で、新しい技術が開発されてから数年必要であることはざらです。
さらに導入のためには、メーカー・システム会社さんとの詳細仕様検討、制作、出荷前の検査などがあります。また、工事の段取りや導入スケジュールを引いていざ工事となります。予算をつけてから1、2年後にようやく装置、技術が導入されます。
また、基本的に導入されれば10年、20年と使っていくものが多くあるため、ものによってはWindows XPが入っているPCも普通にあります(スタンドアローンで。。)。
そんな製造業とは技術導入のスピードが全く異なる機械学習、ニューラルネットワークの分野で、今回は最適化手法について私が理解した内容をまとめたいと思います。
基本的な内容であるSGDから現在よく使用されているADAMまでをそれぞれの特徴と課題に着目してまとめました。
今回、参考にさせて頂いたレビュー論文はこちらです。
On Empirical Comparisons of Optimizers for Deep Learning
https://arxiv.org/abs/1910.05446
概要下記になります。
- 最適化手法の概要
- 最適化手法の変遷
最適化手法の概要
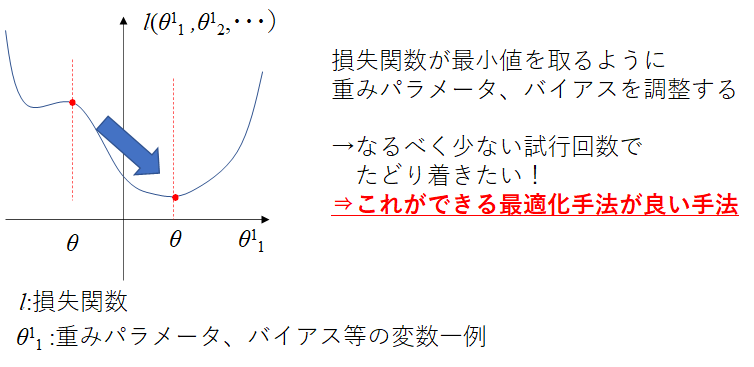
ニューラルネットワークにおいて、モデルの精度を表す関数として損失関数があります。これは、以前の記事でもまとめましたが下記のことを示します。
損失関数は、その得られる値を最小化させることで予測精度の高いモデルへとすることができます。従って、その損失関数が小さくなるようなパラメータを探す必要があります。このとき、このパラメータの微分した値を手掛かりにパラメータを更新していきます。
モデルの精度を上げるためには損失関数を最小化させることが必要であることを確認しました。このとき、最小化させる手法を最適化手法と呼んでいます。
ここで記載しているθ:重みパラメータやバイアスを変化させて、損失関数を最小化させることを考えます。
最適化手法の変遷
SGD(Stochastic Gradient Descent):確率的勾配降下法
1951年(これは古いですね)にRobbinsとMonro氏らによって発表されたアルゴリズムになります。重み$\mathbf{w}$で損失関数$E$を偏微分した値と学習率$\eta$を掛けた値を引いています。
A Stochastic Approximation Method
https://projecteuclid.org/euclid.aoms/1177729586
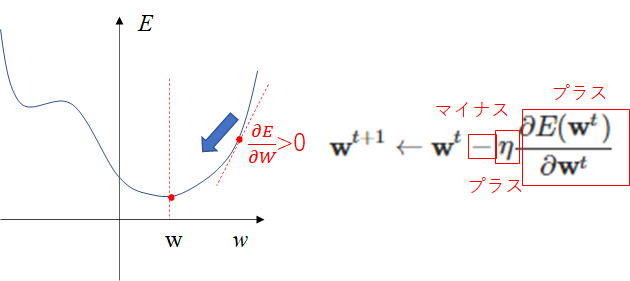
ここで、←の意味は、左辺(t+1番目)の値に右辺(t番目)の値を入れるという意味です。漸化式の考え方と同じですね。
\mathbf{w}^{t + 1} \gets \mathbf{w}^{t} - \eta \frac{\partial E(\mathbf{w}^{t})}{\partial \mathbf{w}^{t}}
偏微分した値は勾配であり、+の勾配であれば引くことで最小値に向かうことがイメージできるかと思います。
ここで$\eta$は固定値(0.01とか0.001とかを取ります)となっているため、モデルを作る人間が手動で値を決める必要があります。勾配の値で最小値に向かっていくため、損失関数によってはハンチングをしたりすることで、収束しないことがあります。
**このように、手動で調整するため自動的に値が最適化されない値をハイパーパラメータと呼びます。**機械学習をさせたい人間としては、この値をなるべく自動で最適化させたい!と思うのが常になります。
次に、この式について、より早く収束に向かわせるように調整したアルゴリズムが下記になります。
Momentum
1964年にPolyak氏ら(旧ソ連)で発表されたアルゴリズムです。
先ほどの式に対して、前回の更新量($\mathbf{w}^{t}$-$\mathbf{w}^{t-1}$)を足した式になります。物理学の力学分野でいうところの慣性と同じ考え方をすることから、Momentum(慣性項)と呼ばれます。$\alpha$はこの慣性項のパラメータになります。
Some methods of speeding up the convergence of iteration methods
https://www.researchgate.net/publication/243648538_Some_methods_of_speeding_up_the_convergence_of_iteration_methods
\mathbf{w}^{t + 1} \gets \mathbf{w}^{t} - \eta \frac{\partial E(\mathbf{w}^{t})}{\partial \mathbf{w}^{t}} + \alpha( \mathbf{w}^{t}-\mathbf{w}^{t-1})
先ほどの勾配がプラスとなる場合を考えます。$\mathbf{w}^{t}$よりも$\mathbf{w}^{t-1}$の値が大きいことから、結果として最後の慣性項は-の値となります。従って、SGDよりも早く収束に向かうことが想像できます。
物理の力学のように物体が運動している考え方を取り入れたものになります。
しかしながら、この場合も学習率$\eta$や$\alpha$はある値を取っている定数であるため、最適化が自動で行えない課題が残っています。
従って、次はこの学習率を自動で調整してくれる仕組みを取り入れることを先人は考えました。
AdaGrad
2011年(急に最近になりました)にJohn Duchi氏らによって発表されたアルゴリズムです。初期値として学習率$\eta_{0}$を決める必要はあります。また、最後の式自体はSGDと同じ式に見えます。
しかし、$\eta$は重みパラメータ$w$の関数となっていることが分かります。
パラメータ$\epsilon$は、無限大に発散させないように小さな正の定数を設定しています。
(PDFです)Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
http://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf
h_{0} = \epsilon\\
h_{t} = h_{t−1} + \nabla E(\mathbf{w}^{t})^{2}\\
\eta_{t} = \frac{\eta_{0}}{\sqrt{h_{t}}}\\
\mathbf{w}^{t+1} = \mathbf{w}^{t} - \eta_{t}\frac{\partial E(\mathbf{w}^{t})}{\partial \mathbf{w}^{t}}
学習率を勾配によって変わる変数としています。勾配の2乗となっています。従って必ず正の値を取ります。その値が加算されていくため、それを分母に取る学習率は徐々に低い値を示していきます。これは、最適点に落ち着かない現象を回避してくれる効果があります。
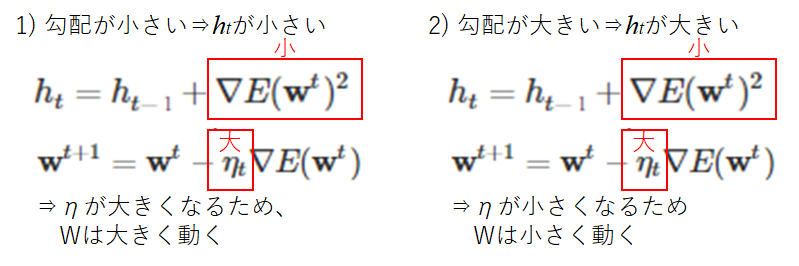
さて、学習率が変化するようになったことで落ち着いて最適点に収束していきそうな気がします。しかしここでも課題が出てきます。学習回数(epochs)を重ねていくと、更新量が0に近づいて行ってしまうため更新がされなくなってしまいます。最適点に落ち着いていない場合はこれでは問題です。
従って、それを解決しようとした考えが次のRMSPropになります。
参考URL
Adagradによる最適化
https://www.renom.jp/ja/notebooks/tutorial/basic_algorithm/adagrad/notebook.html
RMSProp
2012年にTijmen Tieleman氏らによって発表されたアルゴリズムです。
先ほどの$h$についてみると、過去全部を用いるわけではなく、直近の勾配の二乗和をとるようになっています。$\alpha$は0.99などの値を指定します。すると下記$h$に関する式について、第2項の値が小さい一方で第1項の方が値が大きくなることが分かります。
つまりAdaGradよりも$\alpha$の値を調整することで直近とそれより以前の勾配の影響どちらを考慮させたいかを適切に選んで最適化に向かわせることができます。
h_{t} = \alpha h_{t−1} + (1 - \alpha) \nabla E(\mathbf{w}^{t})^{2}\\
\eta_{t} = \frac{\eta_{0}}{\sqrt{h_{t}} + \epsilon}\\
\mathbf{w}^{t+1} = \mathbf{w}^{t} - \eta_{t} \nabla E(\mathbf{w}^{t})\\
AdaDelta
2012年にMatthew氏らによって発表されたアルゴリズムになります。(この辺りから理解に時間がかかるようになりました。。)
先ほどのRMSPropと同じ考え方となっています。直近の勾配二乗和を使おうとしていることが分かります。
ADADELTA: An Adaptive Learning Rate Method
https://arxiv.org/abs/1212.5701
h_{t} = \rho h_{t−1} + (1 - \rho) \nabla E(\mathbf{w}^{t})^{2}\\
v_{t} = \frac{\sqrt{s_{t} + \epsilon}}{\sqrt{h_{t} + \epsilon}} \nabla E(\mathbf{w}^{t})\\
s_{t+1} = \rho s_{t} + (1 - \rho) v_{t}^{2}\\
\mathbf{w}^{t+1} = \mathbf{w}^{t} - v_{t}
ADAM
そして最後に、現在多くの最適化手法として用いられているADAMについてです。これは、2015年にKingma氏らによって発表されたアルゴリズムになります。Adamとは、Adaptive(適応性のある)、Moment(運動量)、Estimation(見積)の略になります。
考え方としては、Momentumで出てきた物理法則に準じる動きを取り入れることと、AdaGradで出てきた学習率を適宜変化させていくことを取り入れたハイブリッドなアルゴリズムになります。
Adam: A Method for Stochastic Optimization
https://arxiv.org/abs/1412.6980
m_{t+1} = \beta_{1} m_{t} + (1 - \beta_{1}) \nabla E(\mathbf{w}^{t}) ;勾配の1乗を溜め込む\\
v_{t+1} = \beta_{2} v_{t} + (1 - \beta_{2}) \nabla E(\mathbf{w}^{t})^{2}:勾配の2乗を溜め込む\\
\hat{m} = \frac{m_{t+1}}{1 - \beta_{1}^{t}}\\
\hat{v} = \frac{v_{t+1}}{1 - \beta_{2}^{t}}\\
\mathbf{w}^{t+1} = \mathbf{w}^{t} - \alpha \frac{\hat{m}}{\sqrt{\hat{v}} + \epsilon}
また、$\hat{m}$や$\hat{v}$はバイアス補正と呼ばれる値となっています。これは、ある定数によって割った値を示しています。通常、$\beta_{1}$は0.9、$\beta_{2}$は0.999を示します。
AdaGradやRMSPropは学習率だけに対して調整を行うようなものをAdamは勾配の2乗平均と平均を1次モーメントと2次モーメントとして考慮することで、パラメータごとに適切なスケールで重みが更新されることを可能にしました。
現在(2020年初頭)はこのADAMをさらに高精度なものにしていくか、が最適化手法研究の流れの一部なようです。
終わりに
今回、確率的勾配降下法(SGD)から現在よく使用されているADAMについてその考え方に重きを置いてまとめました。人間の知恵によってアルゴリズムが改善していくことが実感できました。しかし、ADAMにおいても結局ハイパーパラメータは残っており、モデルごとに適切な値を選択する必要があります。
次回は考え方が分かりましたので、実際の関数を使ってその収束の仕方、最適化にどんな違いが表れるのか比較検証してみたいと思います。
最後に、表現等に誤りや語弊がありましたらコメントを記載して頂けると幸甚です。ここまで閲覧頂きありがとうございました。
以下に参考にさせて頂いたURLを記載します。
Optimizer : 深層学習における勾配法について
https://qiita.com/tokkuman/items/1944c00415d129ca0ee9#%E3%81%BE%E3%81%A8%E3%82%81
Optimizer入門&最新動向
https://www.slideshare.net/MotokawaTetsuya/optimizer-93979393
俺はまだ本当のAdamを理解していない
https://qiita.com/exp/items/99145796a87cc6cd47e1
勾配降下法の最適化アルゴリズム
https://www.slideshare.net/nishio/ss-66840545