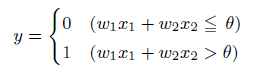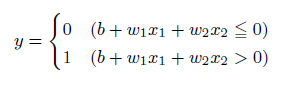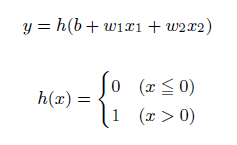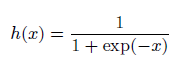3層順伝搬型ニューラルネットワークを自作して、計算を深く理解しようとした

#はじめに

　機械学習や深層学習はライブラリが豊富なため、簡単なコピペにより予測が可能になっています。私自身も多くの先人が作ったプログラムを動かして概要は分かるようなレベルになってきました。
　特に、深層学習（ニューラルネットワーク）に関してはＧＡＮや自然言語処理に応用されています。目まぐるしく新しい技術が生み出されているジャンルであり、社会・産業への応用が迅速に進んでいると思っています。従って、そのような変革の中心にある技術と認識しており、非常に興味深くこれら分野について深く理解したい！という動機があります。

　現在、ディープラーニングの教科書として有名なこちらで基礎から学び始めております。
https://www.oreilly.co.jp/books/9784873117584/
　今回、ニューラルネットワークをほぼ一から構築することで（numpyは使用しますが）、そこで行われている計算を実感を持って理解したいと思います。

　要約としては下記です。

• パーセプトロンを理解する
• ニューラルネットワークに展開する
• 3層のニューラルネットワークを実装する

##パーセプトロンを理解する

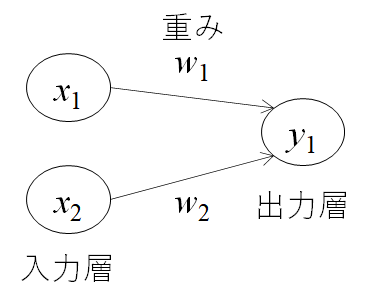
　　パーセプトロンとは、複数の信号を入力として受け取り、一つの信号を出力することを示します。機械学習の分野では、信号を出力しないことは０、信号を出力することを１として扱います。

　

　この考えを簡単に図にしたものが上の図になります。xは入力信号、yが出力信号、wが重みを表します。この〇はニューロンと呼ばれます。ニューロンには、重みと入力の値を掛けた総和が送られます。この時、総和が閾値θを超えたときに出力１を出します。下記の式になります。

###AND回路で確認してみる

　それでは、実際にプログラムを作ります。上記の図で示している簡単なパターンを再現しました。
　まず、閾値が０．４の時で計算してみましょう。

NN.ipynb

def AND(x1,x2):
    w1,w2,theta = 0.5,0.5,0.4
    tmp = x1*w1 + x2*w2
    b = -0.5
    if tmp <= theta:
        return 0
    elif tmp > theta:
        return 1

print(AND(0,0))
print(AND(1,0))
print(AND(0,1))
print(AND(1,1))

0
1
1
1

　結果として、x1,x2どちらかが1であれば出力として1を吐き出すことが分かりました。一方、閾値を0.7とすると、下記のようになります。

print(AND(0,0))
print(AND(1,0))
print(AND(0,1))
print(AND(1,1))
0
0
0
1

x1,x2どちらかだけが1だと出力で1を吐き出さなくなりました。閾値の設定により得られる出力が変わることが確認できます。

##ニューラルネットワークに展開する
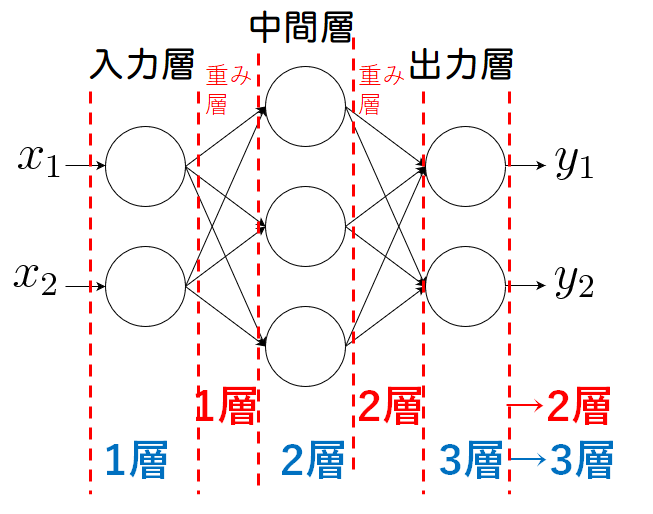
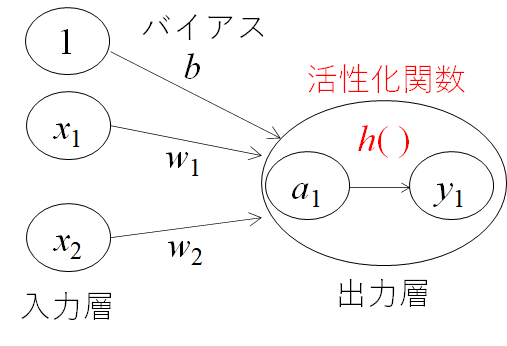
　多層パーセプトロンとは、入力層と出力層の間に中間層と呼ばれる層があるネットワークのことです。本によっても記載が異なる場合がありますが、下記図の場合入力層を0層、中間層を1層、出力層を2層と呼ぶことにしています。

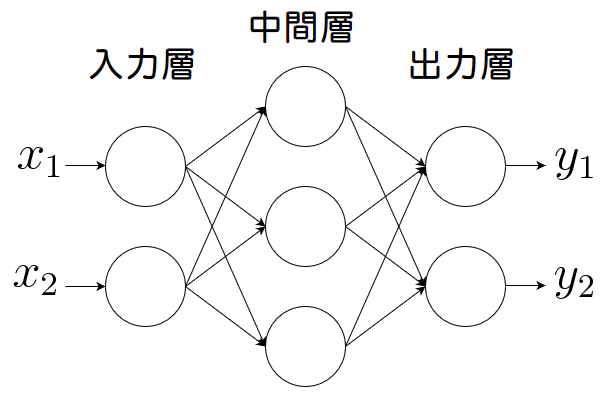
###ニューラルネットワークの層の数え方

　ここで、〇層のニューラルネットワークと呼ぶ際の数え方には流儀（慣習？）があるようです。重み層を数えたり、あるいはニューロンの層を呼ぶ場合もあるようです。どちらが一般的かは私も経験があまりありませんが、オライリーの教科書に習って重み層ベースで名付けたいと思います。

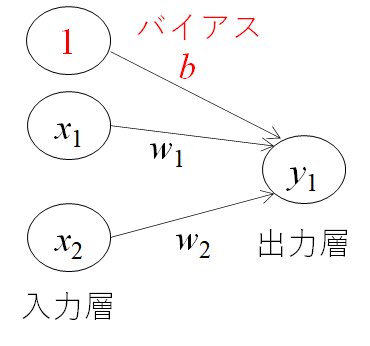
###バイアスを理解する
　

　次に、バイアスｂと呼ぶ値を導入します。先ほどの閾値θを―ｂとして先ほどの式を整理すると上式のように、０を基準にしてｙの出力を０か１に決めることが可能になります。バイアスとは、小職の業界（製造業）では「下駄をはかせる」補正値の意味合いで、値を全体的にｙ軸に上下させることが可能となります。

###活性化関数を理解する
　

　ｙが０か１かを判別させる関数を活性化関数と呼びます。この活性化関数によって得られる値は０か１近辺の値とすることができるため、計算の発散を防ぐことができる機能もあります。
　この活性化関数はいくつか種類があります。

• シグモイド関数

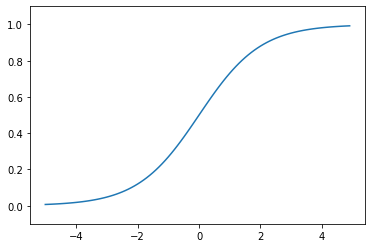
　活性化関数でよく使われる関数の一つです。下記のような自然対数の底であるネイピア数eの関数の分数、になります。ぱっとこの関数の形は思い浮かびにくいのですが、描くくと下記のようになります。

NN.ipynb

import numpy as np
def sigmoid(x):
    return 1/(1+np.exp(-x))


xxx = np.arange(-5.0,5.0,0.1)#sigmoid関数を表示
yyy = sigmoid(xxx)
plt.plot(xxx,yyy)
plt.ylim(-0.1,1.1)
plt.show

ｘ＝０を境にｘ＞０では徐々にｙ＝１に漸近していくことが分かります。また、逆にｘ＜０ではｙ＝０に漸近していくことが分かります。入力した値を０～１の間で出力させることができる点が、活性化関数の役割を果たせているため、非常に便利であることが分かります。

• ステップ関数

　次に、先ほどのシグモイド関数をさらに極端に０，１を出力させる関数としてステップ関数があります。
これは下記のように書くことになります。

NN.ipynb

def step_function(x):
    return np.array(x > 0, dtype=np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
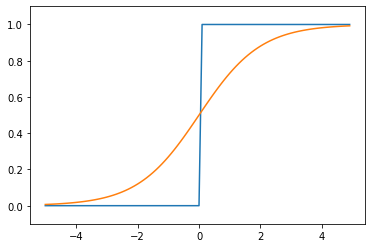
plt.plot(xxx,yyy)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) 
plt.show()

青がステップ関数で、オレンジがシグモイド関数になります。出力値を０か１しかとらないことが良く分かります。この関数の使い分けに関しては、私自身感覚が薄いところもあるため、今後の宿題とさせてください。
感覚としては、シグモイド関数のほうがより細やかに値を取ることが可能であるため、微妙な入力差でも違いを区別できる機能を有していると理解しています。一方で、多層で計算負荷が高い場合は、適宜ステップ関数を利用することで負荷を下げつつ判別させることができる使い分けをするのではないかと思います。

• 非線形関数（ReLU関数）

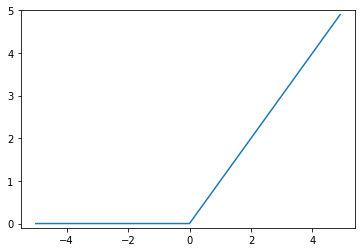
　最後に、こちらもよく使われている印象があるReLU(Rectified Linear Unit)関数についてです。ｘが０を超えていれば、その値をそのままｙとして出力し、０以下なれば０を出力する関数になります。

NN.ipynb

def relu(x):
    return np.maximum(0,x)

xx = np.arange(-5.0,5.0,0.1)
yy = relu(xx)
plt.plot(xx,yy)
plt.ylim(-0.1,5)
plt.show

###順伝搬型ってなに
　
　今回、順伝搬型のニューラルネットワークを作ります。この順伝搬型とは、入力から出力に一方向に流れていくことを示しています。モデルの学習を考える際は、逆に出力から入力へ向かって計算を行います。これは逆伝搬法と呼びます。

##3層のニューラルネットワークを実装する

　さて、実際に3層のニューラルネットワークを記述していきたいと思います。

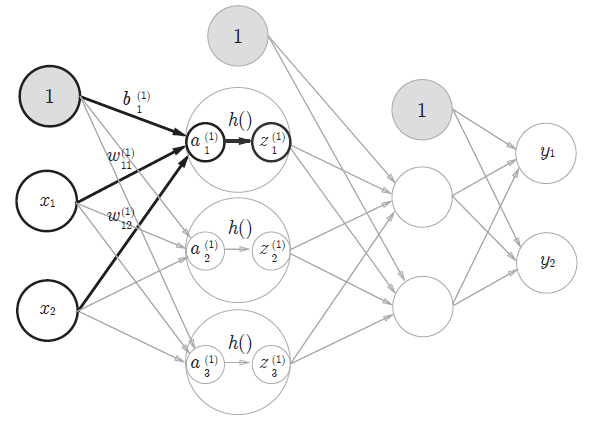
　上図で記されている3層のニューラルネットワークを作ることを考えます。
　まずは、上図の太字で目立っている計算だけを下記に取り出してみます。

NN.ipynb

def init_network():
    network = {}
    network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
    network['b1'] = np.array([0.1,0.2,0.3])
    return network

def forword(network,x):
    W1= network['W1']
    b1= network['b1']
    
    a1 = np.dot(x,W1)+b1
    z1 = sigmoid(a1)
    
    return y

network = init_network()
x = np.array([2,1])
z1 = forword(network,x)
print(z1)

[0.40442364 0.59557636]

init_network()関数に重みやバイアスを定義させ、forword()関数に実際に計算させる式を定義させました。後は、その関数を呼び出して初期値のｘを代入させて答えを吐き出せるようにしています。ずらっと関数を定義せずに記述するよりも分かりやすいですね。

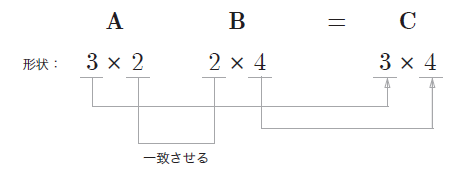
　また、ここでnp.dotとして記載している行列の内積を表す関数にも注意が必要です。行列の積は、掛け算の順番で得られる行列の次元が変わることから、記述の際は注意しましょう。

###3層のニューラルネットワーク

NN.ipynb

def init_network():
    network = {}
    network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
    network['b1'] = np.array([0.1,0.2,0.3])
    network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
    network['b2'] = np.array([0.1,0.2])
    network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
    network['b3'] = np.array([0.1,0.2])
    return network

def forword(network,x):
    W1,W2,W3 = network['W1'],network['W2'],network['W3']
    b1,b2,b3 = network['b1'],network['b2'],network['b3']
    
    a1 = np.dot(x,W1)+b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1,W2)+b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2,W3)+b3
    y = softmax(a3)
    
    return y

　二つの関数に最後まで記述させるとこのような書き方になります。さて、ここで先出ししましたがsoftmaxと書かれた記述が最後にあります。これについて次でまとめました。

###恒等関数とソフトマックス関数
　あとは、この二つの関数に層を付け加えていけば良いことが分かります。そして、最後に出力する値ｙについて考えます。
　数字の０～９種類を当てる問題など分類を行う必要がある場合は、それぞれの種類に該当する確率を出力させ、一番確率が高いものを予測値とします。そのような確率として表すうえで便利な関数がソフトマックス関数です。

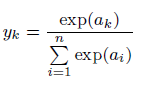
ある分類の項目すべてで取る値の総和を分母とし、個別の取る値を分子とすることで確率を表す値とすることができます。
このソフトマックス関数で終えることで分類問題を確率へ帰着させ、最も高い値を予測値としているのです。
　

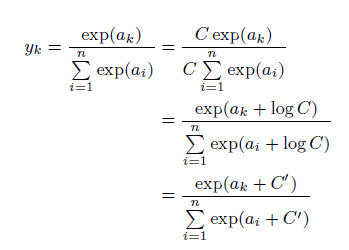
　実装上では、expの指数関数であるため、非常に値が発散しやすくなる課題があります。
　従って、ある定数を分母、分子にかけてexpの指数に入れ込むことで発散しにくくなることを便宜上行っておくことがよくあるようです。

NN.ipynb

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a-c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a/sum_exp_a
    return y

###初期条件を入力し、答えを出力させる

NN.ipynb

network = init_network()
x = np.array([2,1])
y = forword(network,x)
print(y)

[0.40442364 0.59557636]

試しに、ｘへ適当な値を入れてみたところ、下記のように答えが返ってきました。
ｙ１が４０％、ｙ２が６０％の確率であることを示す値が出力されました。
後は入力の行列が大きくなったり、層が深くなる（≒増える）ことで複雑な分類を行えるようになっていくと理解しています。

#終わりに

　今回、非常にベーシックなニューラルネットワークを手作りしました。手を動かしてみるだけでかなり理解が深まりました。
　**なんとなくコピペして動かしたＧＡＮアルゴリズムの基礎の基礎、をようやっと分かるようになりました。**ここに、モデルの学習や畳み込みといった考えを入れることで畳み込みニューラルネットワークへ、さらにＧＡＮへ繋がっていくのでしょう。
　最新の技術へたどり着くにはまだまだ序章かもしれませんが、このようにまとめて着実に理解を深めることで確実に自分の技術力アップにつなげていければと思います。

プログラム全文はこちらです。関数で遊んだだけのファイルと3層ニューラルネットワークのファイルに分かれています。
https://github.com/Fumio-eisan/neuralnetwork_20200318