はじめに
ベイズ統計学を学ぶ上で期待値をおさらいしました。
下記本を参考にしました。
期待値とは
期待値(expectation)とは、ある関数$f(x)$の確率分布$p(x)$のもとでの$f(x)$の平均値のことを指します。表記としては、$E[f]$と書きます。
離散分布では以下のように表します。
E[f] = \sum_x p(x)f(x)
一方、連続変数の場合は積分として表すことができます。
E[f] = \int p(x)f(x)dx
エントロピー
確率分布$p(x)$に対する次のような期待値をエントロピー(entropy)と呼びます。
\begin{align}
H[p(x)]& = - \sum_x p(x) ln(p(x))\\
\end{align}
有限和での近似(モンテカルロサンプリング)
分布$p(x)$から独立に抽出されたサンプルの集合を$\bf {z}^{(n)} (n = 1,...,N)$としたとき、期待値は下記のように近似できます。
E[f] = \frac{1}{L} \sum_{n=1}^{N}f(\bf{z}^{(N)})
となります。
ここで例題で考えます。
例題
$p(x=1)=0.3,p(x=1)=0.7$となるような離散分布を考えます。
エントロピーの定義からエントロピーは
\begin{align}
H[p(x)]& = - \sum_x p(x) ln(p(x))\\
&=-(p(x=1)lnp(x=1) + p(x=0)lnp(x=0) )\\
&= -(\frac{3}{10}ln\frac{3}{10}+\frac{7}{10}ln\frac{7}{10})\\
&=0.610
\end{align}
となります。
さて、これを有限和で近似する場合の計算をしてみます。random.uniformメソッドにより0~1の無作為な値を出力させて、それが$p(x=1)=0.3$よりも大きくなるかどうかで$x=1$か$x=2$かどうかを判別させています。
そして、$x=1,2$となる回数をcntで数えさせることをしています。
下記のようなプログラムになります。試しに1000回計算しています。
cnt = []
proba_1 =[]
proba_2 =[]
time = 1000
a = random.uniform(0,1)
exp =[]
for i in range(time):
a = random.uniform(0,1)
if a > p1:
cnt = np.append(cnt,1)
else:
cnt = np.append(cnt, 0)
proba_1 = np.append(proba_1, (i+1-sum(cnt))/(i+1))
proba_2 = np.append(proba_2, sum(cnt)/(i+1))
exp = np.append(exp, -(((i+1-sum(cnt))*math.log(p1))+((sum(cnt))*math.log(p2)))/(i+1))
plt.xlabel('time')
plt.ylabel('probability')
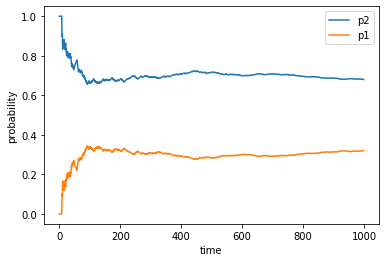
plt.plot(time_plot, proba_2, label="p2")
plt.plot(time_plot, proba_1, label="p1")
plt.legend()
$p(x=1)=0.3,p(x=2)=0.7$に大よそ100回以降収束していくことが分かりました。
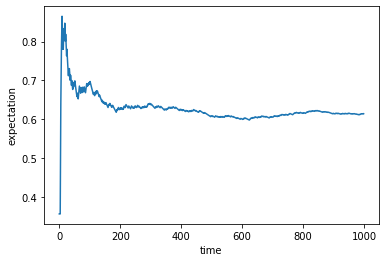
こちらも100回以降で元々求めていた期待値(=エントロピー)の0.61あたりに収束していることが分かりました。
確かにこの期待値近似の手法が問題ないことが確認することができました。
終わりに
今回は非常に簡単な例題だったため、算出及び確かめることが容易でした。しかし、実際の問題では期待値が解析的に求めることが難しい場合がほとんどです。
従い、このモンテカルロサンプリングで近似することを覚えておくと有益なのだと思います。
プログラ全文はこちらです。
https://github.com/Fumio-eisan/VI20200520