前書き
備忘録のつもりです
間違い等含むかもしれません
量子コンピューティング 基本アルゴリズムから量子機械学習までのP. 77, 78の内容が個人的に難しかったためそれについていろいろ書いていこうと思います
ここの内容の元論文はQuantum principal component analysisのようです
私は物理ではなくコンピュータ系の人間なので量子力学の知識があまり無いですが、本はここのページから割と突然に(?)量子力学の知識をやや使ってきていたようでありまして、ここで苦戦したという具合です
そういった知識不足のため以下ではしっかりとした量子力学的な説明というよりも「コンピュータ系の人が量子コンピュータを使おうとしたときの把握の仕方」をしています
計算などはこちらのページに大変詳しく書かれていらっしゃいましたので、この記事ではさらにその周辺知識をまとめます
密度行列
純粋状態と混合状態、密度行列の細かい説明は他に譲りますが(自信がない)、何でもエンタングルした複数量子ビットの、一部分だけに注目したときにはそれが混合状態となってしまいベクトルの形ではなく密度行列でしか書けない、ということだそうです(本だとP.52)
ここは古典コンピュータを触ることばかりやっていた私にとっては意味不明ポイントですね
5bitあるうちの2bitに注目したければ単にほかのbitを無視すればいいので
量子は他の量子とは影響関係があるから単に無視できないということでしょうか
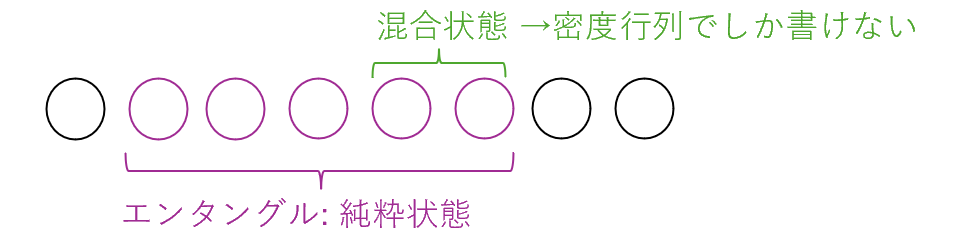
図で言うと、右の2量子ビットの状態だけを抜き出して書き表したいとき、密度行列を用いることとなるようです
(全体5量子ビットがエンタングルしているために、その状態ベクトルを5つの2次元ベクトルのテンソル積の形に分解できないため。分解できるなら単にその量子ビットに対応するベクトルを無視すればよい。)
Matrix Density Exponentiationの計算では、一部の量子ビットの状態にのみ注目することで得たい計算結果を得られるということなので、必然的にその説明には密度行列を用いることになるようです
と言っても、とりあえずはそんなに難しいことは無く、まず$\ket{\psi}$という純粋状態の、密度行列での表記法は
\ket{\psi}\bra{\psi}
とするだけです。
ゲートの適用については、ベクトルでの表記法だと
\ket{\psi} \longrightarrow U\ket{\psi}
という具合でしたが、密度行列では
\ket{\psi}\bra{\psi} \longrightarrow U\ket{\psi}\bra{\psi}U^{\dagger}
と両方から挟めばよいだけです。
また、量子コンピュータでは計算基底しか使わないと思うので、それならば各状態の観測確率は、密度行列の対応するインデックスの対角要素の値そのままです。これは混合状態が純粋状態の線形和で書けることを考えるとすぐにわかります(詳細略)。
また複数量子ビットあるときも、ベクトルでの表記と同じように、密度行列のテンソル積をとればよいです。逆に、エンタングルメント状態の時、テンソル積に分解できません
部分トレース
それでは実際にエンタングルした量子ビットの一部分のみに着目し、その部分の量子状態を、密度行列を用いて書きます
これには部分トレースという計算をするとよいそうです
まず部分トレースとは、テンソル積$C=A \otimes B$とあったときに、$A$または$B$についてのみトレースをとる計算です。つまり
\begin{align}
\mathrm{Tr}_{A}(C)&=\mathrm{Tr}(A)B\\
\mathrm{Tr}_{B}(C)&=\mathrm{Tr}(B)A
\end{align}
のような計算です。しかし、$C$がテンソル積に分解できない場合もあります。このときは、上の定義に従い、要素ごとに見ていった場合
C
=
\begin{bmatrix}
\color{orange}{a_{11}B} & a_{12}B \\
a_{21}B & \color{orange}{a_{22}B}
\end{bmatrix}
となりますから、
\mathrm{Tr}_{A}(C):=\mathrm{Tr}(A)B=(a_{11}+a_{22})B=\color{orange}{a_{11}B}+\color{orange}{a_{22}B}
のようになるので、ブロック対角要素を足すというのを$\mathrm{Tr}_A$とします
一方$\mathrm{Tr}_B$については、上の$C$の各$B$において$\mathrm{Tr}$、つまり
\mathrm{Tr}_{B}(C):=\mathrm{Tr}(B)A
=
\begin{bmatrix}
a_{11}\mathrm{Tr}(B) & a_{12}\mathrm{Tr}(B) \\
a_{21}\mathrm{Tr}(B) & a_{22}\mathrm{Tr}(B)
\end{bmatrix}
のような計算になります。つまり、各ブロック行列について$\mathrm{Tr}$をとればよいです。このように要素ごとに注目すれば、一般の行列にも部分トレースの計算ができます。
量子コンピュータの話に戻すと、上での各行列$A,B,C$が密度行列となります。非対角要素の扱いへの理解が怪しいですが、対角要素の各インデックスが対応する状態を得られる確率であることを踏まえると、対角要素のみに注目すれば、これが確率の周辺化の計算になっていることはわかると思います。つまり、$\mathrm{Tr}$した方の量子ビットは、各状態の確率の和をとり周辺化で消滅、$\mathrm{Tr}$してないほうの量子ビットの確率を残した、ということになります。$\mathrm{Tr}$した方は無視されることとなり、それを「トレースアウトする」と言うそうです。
(密度行列は$\mathrm{Tr}$したら必ず1になることに注意)
これで、全体の状態を表す密度行列の部分トレースをとることで、一部の量子ビットの状態を取得できるようになりました。
密度行列冪を利用した量子位相推定
そもそも密度行列冪 (Matrix Density Exponentiation) とは何かといえば、行列$\tilde{A}$を、(そうでなければ)エルミート行列化した
A
=
\begin{bmatrix}
O & \tilde{A} \\
\tilde{A}^\dagger & O
\end{bmatrix}
という行列の指数関数$e^{iAt}$を任意の量子状態に効率よく作用させる方法でした。
行列指数関数の性質として
A\ket{\psi}=\lambda\ket{\psi}
とすると($\lambda$が$A$の固有値)、
e^{iAt}\ket{\psi}=e^{i\lambda t}\ket{\psi} \tag{1}
という風になります。
ところで、一般的な量子位相推定は、
U\ket{\psi_0}=e^{i2\pi\phi}\ket{\psi_0}
の$\phi$(固有値の位相)を求める計算でした。つまり右辺の指数関数の指数部をおろしてくる計算なわけですが、式(1)でも同じように指数部をおろすことができれば、位相ではなく直接固有値が求まりそうです。
つまり、量子位相推定のアルゴリズムにおいて、$U$を$e^{iAt}$に置き換える方法が考えられます
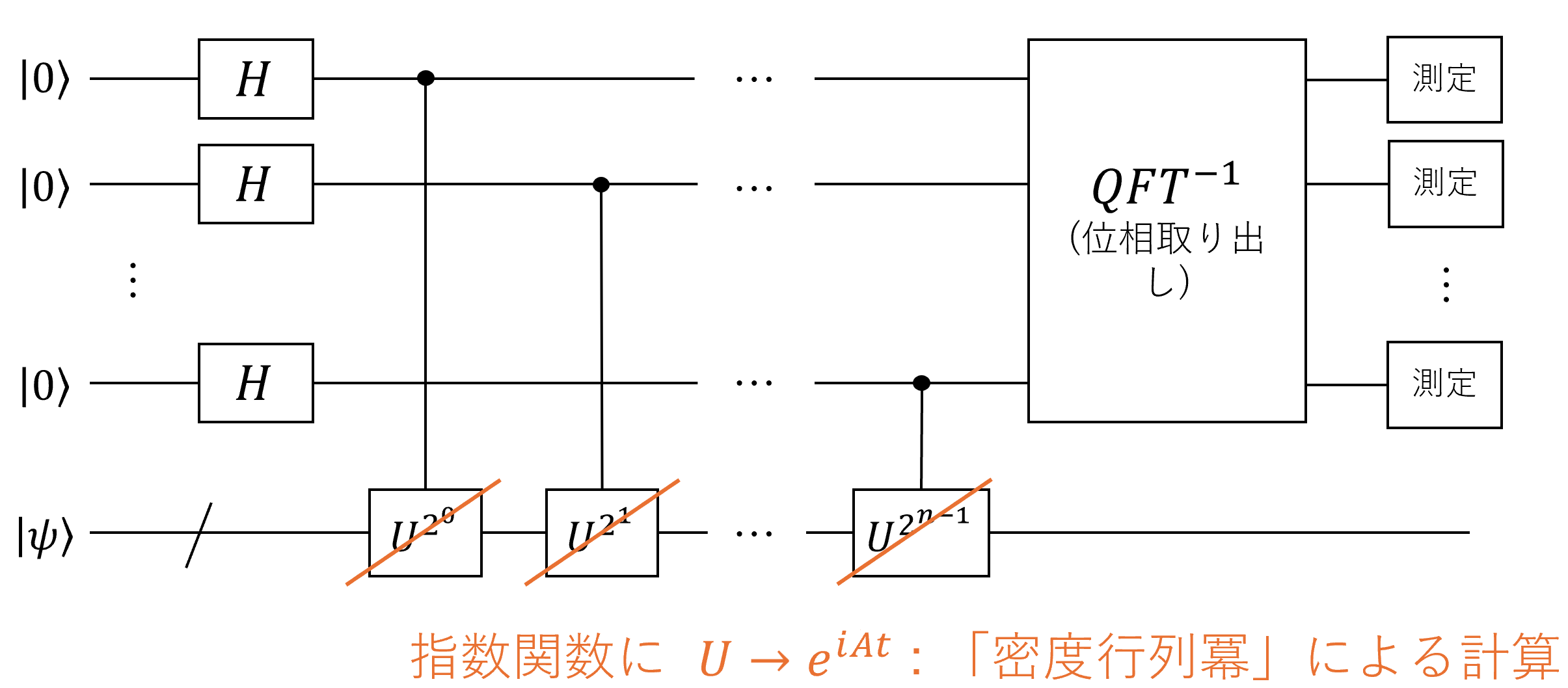
これがHHLアルゴリズムとかで利用できそうだ、という話なんだと思います。
(指数回の$e^{iAt}$の掛け算のために指数個の$A$の用意が必要な気がするけど、大丈夫なのかとかよくわからなかった)
前書きで挙げた本やQuantum principal component analysisの論文だと(というかHHLの元論文でも)、上の量子回路図の左半分を数式1本で述べているようで、例えばその本では
\sum_{k=1}^{n} \ket{k}\bra{k} \otimes \sigma \otimes \rho^{(1)} \otimes \rho^{(2)} \otimes \ldots \otimes \rho^{(n)}
に対し、ゲート
\sum_{k=1}^{n} \ket{kt}\bra{kt} \otimes \prod_{g=1}^{k}e^{-i \mathcal{S}_g t}
を作用させる (ここの$\sum_{k=1}^{n} \ket{kt}\bra{kt}$は本当は$\ket{kt}$が$\ket{k}$だと思う)、といった具合に述べられており、難しいです。
上の量子回路図を見れば、この上の式の$\sum_{k=1}^{n} \ket{k}\bra{k}$はアダマールゲートを通過後の量子状態に対応しているんじゃないかと思います。
そして、ゲートの方の$\sum_{k=1}^{n} \ket{k}\bra{k}$なんですが、これが「条件付き」のゲート計算に(ちょっと違うが)対応しているようで、つまり、ゲートを適用してみた
\left( \sum_{k=1}^{n} \ket{k}\bra{k} \otimes \prod_{g=1}^{k}e^{-i \mathcal{S}_g t} \right)
\left(\sum_{k=1}^{n} \ket{k}\bra{k} \otimes \sigma \otimes \rho^{(1)} \otimes \rho^{(2)} \otimes \ldots \otimes \rho^{(n)} \right)
の計算は、一見すると$\sum$があって、掛け算は全部の項の組み合わせ、大量の項が出てくるように見えますが、$\ket{k}$は正規直交基底なので、実は考える必要があるのは右と左で同じ$k$である項のみです。つまり例えば、$\ket{k_1}\bra{k_1}\ket{k_2}\bra{k_2}$となる項は消えてしまいます。つまり、展開すると、
\sum_{k=1}^{n}
\ket{k}\bra{k} \otimes \left( \prod_{g=1}^{k}e^{-i \mathcal{S}_g t} \right)(\sigma \otimes \rho^{(1)} \otimes \rho^{(2)} \otimes \ldots \otimes \rho^{(n)})
のように書けます。ここで、$\braket{k|k}=1$を利用しています。
この式を解釈すると、つまり、図では上のもともと$\ket{0}$でアダマールゲートを通過した部分が1のとき、SWAPを1回、2のときSWAPを2回、といった具合になります。
ここでよくよく回路図を見てみると、$\ket{k}$の2進表記を考えれば図において$U$の掛けられている回数とすぐ上で述べたSWAPの回数がうまいこと一致していることがわかると思います。桁で考えるか、数値で考えるか、みたいなです。
このように、$\ket{k}$が直交することを利用して、ゲートにおいて$\sum_{k=1}^{n} \ket{k}\bra{k}$を「$\ket{k}$のとき」という意味で利用するというテクニックはしばしばみられるように思います。
またHHLの論文やqPCAの論文だと、この$\ket{k}$を$\ket{\tau}$や$\ket{n\Delta t}$などと表記しており、直後のQFTを踏まえてこれらが時間領域で行われているということを強調しているようです。これらは量子力学を通らず量子コンピュータに無理やりいきなり入った人にとっては、ケットベクトルの扱い方が意味的に?異なっており、いままで数字かベクトルを表す文字しかケットベクトルに入れてこなかった人にとっては、ちょうど一番最初に扱った$\ket{\uparrow}$のような扱い方の急な再来には対応できず理解に手古摺りました。
また、量子アルゴリズムというのは非常に非直感的で、私からすれば、ともすればマジックと区別がつきません。密度行列冪もなんで思いつくのかよくわかりませんでした。なんとなくですが、指数関数の一次近似
e^{-i\rho t}\sigma e^{i\rho t} \approx \sigma + i(\sigma \rho - \rho \sigma)t
を見れば、量子力学に詳しい人だと何か思うところがあるのでしょうか。0次の項は単位行列でもかけておけばと思いますが、1次の項が難しい。SWAPゲートと、$\sigma \rho$または$\rho \sigma$に何か関係でもあるのでしょうか。SWAPテストとか。
また、ゲートをユニバーサル・セット・ゲートに分解するのはコンパイラの仕事だそうで、個人的に、しばらくそのことを見逃しており、どうやってゲートを実際に作るのかでやや混乱していたのでその旨も残しておきます。SWAPゲートは疎なのでその指数関数も多項式個のゲートに分解できるということなのでしょうか。