共分散$$cov(x,y)=(x-\bar x)(y-\bar y)$$は、よく散布図の関係を例に説明していることが多いが、抽象的な説明や理解だとで主成分分析だったりGauss過程を考える際には難しくなると思う。
そこで、自身の理解のために共分散がどういう性質を持っているのかをイチから考えよう。
前提知識
どうしても、深く使いこなすには線形代数の知識が必要です。
とくに内積$u\cdot v=|u||v|\cos\theta$、
多次元のベクトル、行列演算の線形写像性
$$u=Av \qquad \mathrm{as}\qquad u_i=\sum_jA_{ij}v_j$$
$$u\cdot v=u^Tv$$
はよく使います。
※印特に断りがない限りベクトルはn行1列の行列と見なす
まとめ
- サンプルX,Yを、それぞれ一列に並べたベクトル$X=(x_1, x_2,...,y_n),Y=(y_1,y_2,...,y_n)$
と考えると分かりやすいよ - 相関性とはサンプル同士の偏り(偏差)が比例関係に従う度合いをいうよ。ベクトルを平行な成分と垂直な成分に分離したとき、平行な成分が大きいほど相関性が高いよ
- 相関係数とはX,Yの偏差をベクトルとしたとき、なす角度のcos値(コサイン類似度)だよ
- 共分散は各々の分散の相乗平均に相関係数をかけたもので、分散を相互相関に対応させた拡張と解釈できるよ
- サンプルは複数の成分をまとめてd次元ベクトルとし、それをサンプリング方向を列方向に並べて行列として議論したほうが楽だよ。そうすると分散と共分散は分散共分散行列でまとめて記述できるよ
- 主成分分析PCAはサンプルを見る座標軸を回転させるとき、各軸が無相関になるような座標軸の向きを得る計算だよ。
- 主成分分析の処理は中身を理解さえしていれば自力実装は簡単だよ。これを使うためだけならscikit-learnは使うまでもないよ
サンプル間の相関性の定義
前提として、サンプル$X,Y$は順序も重要だったとする。すなわち、n番目のデータは$(x_n,y_n)$と対応するサンプルを考える。
このとき、各データをX軸Y軸それぞれに相当するところに点を打っていくことで散布図ができる。
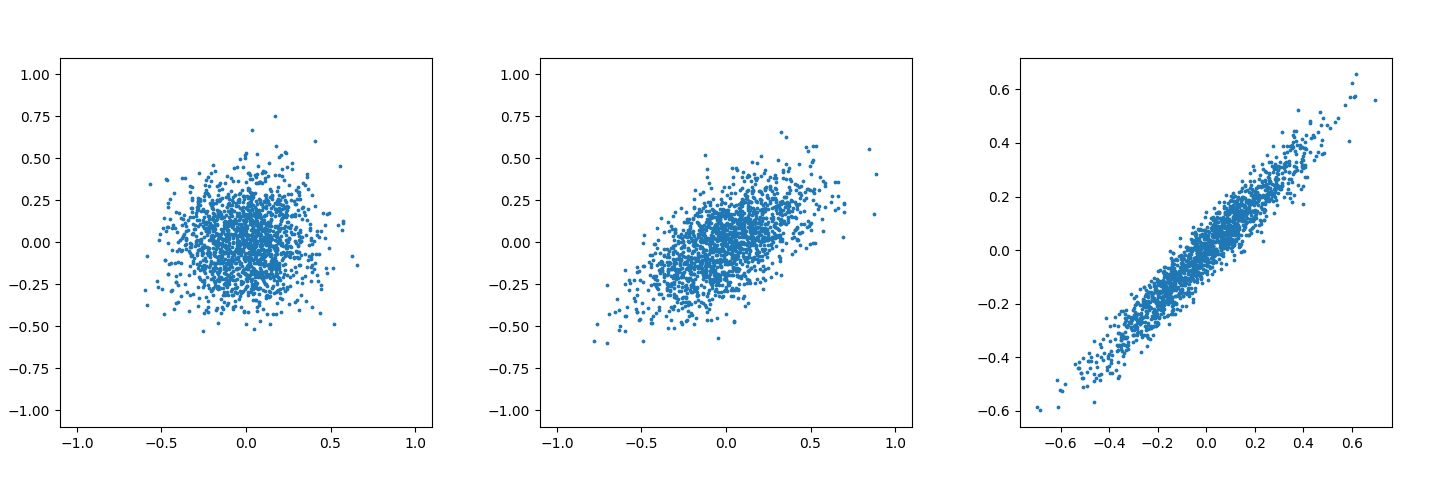
散布図が無相関の場合と弱い相関、強い相関の場合に散布図をプロットすると、以下になる。
2つのサンプル$X,Y$の偏りが比例関係にあるときに、この二つの集団は完全に相関すると定義する。一方、この2つサンプルの偏りが逆の符号で比例関係にあるときも相関する(反相関関係)といっていいはずだ。
偏りが比例関係にあるときを数学的に表すならば、
$$(X-\bar X)=k(Y-\bar Y)$$
であるといえる。ただし、$\bar X, \bar Y$は各サンプルの平均値である。
ここで、X,Yをもう少し具体的に書き下す。X,Yは複数のサンプルを保持しているだろうから、
$$X={x_n}, Y={y_n}$$
であろう。
すると平均値は、
$$\bar x=\sum_n\frac{{x_n}}{N}, \bar y=\sum_n\frac{{y_n}}{N}$$
と定義できる。便宜上、平均値は数列ではなく単値なので、小文字にしておいた。
ここで、
$$S_x={x_n-\bar x}, S_y={y_n-\bar y}$$
はサンプルの平均値からの偏り(右辺は偏差と呼ぶ)を数列化したものである。
ところで、この$S_x,S_y$をN次元空間上のベクトルだと考えよう。冒頭の通り偏差が比例関係
$S_x=kS_y$
のとき相関すると定義した。それは言い換えると、
- 偏差ベクトル$S_x,S_y$が平行であれば相関(反相関)する
といえる。
逆に、相関しないとは$S_x,S_y$が全く上記の関係をみたさないときだろう。
その中間の状態を式でしめすなら。
$$S_x=kS_y+S_z$$
なる、$S_y$と垂直であるベクトル$S_z$がゼロでないときだと該当するだろう。
分散と共分散
分散は、サンプルの偏差の二乗和として定義した値である。
$$v_x=\sum_n\frac{s_{xn}^2}{N}=\frac{S_x^TS_x}{N}$$
これは、偏差ベクトル$S_x$の長さの二乗という見方ができる。
とくに、
$$\sigma_x=\sqrt{V_x}$$
はサンプルXの標準偏差と呼ぶが、これは偏差ベクトルの長さに等しい。
なお、分散はベクトル的や表現としてみれば、自分の偏差ベクトルとの内積である。
一方、共分散は偏差ベクトル同士の内積である。
$$cov(X,Y)=\sum_n\frac{s_{xn}s_{yn}}{N}=S_x^TS_y=\sigma_x\sigma_y\cos\theta$$
つまり、偏差ベクトル$S_x,S_y$の射影で分散を取ることで得られる、と解釈できる。
$\cos\theta$のことをベクトル$S_x,S_y$のコサイン類似度ということもある。
今までの式から$\cos\theta=\frac{cov(X,Y)}{\sqrt{v_xv_y}}$と変形できる。右辺を相関係数と呼び、-1なら反相関、1なら相関、0は無相関である。その間の数値は相関の強度を意味するが、相関強度とはつまりX,Yをそれぞれ一列に並べてベクトルX,Yとみなしたと、ベクトルX,Yのなす角度のcos値(コサイン類似度)であるということがわかる。
無相関の場合$\cos\theta=0$、つまり$S_x,S_y$が直交することに対応することになる。このとき、冒頭の$S_x=kS_y+S_z$とするためのkは0(=比例しない)である場合と対応することからも辻褄が合う。
なお、念のため与えられた偏差$S_x,S_y$に対する比例係数kの出し方は以下である。
$$S_x^TS_y=kS_y^TS_y+S_z^TS_y=kS_y^TS_y$$
なお、$S_z^TS_y$は$S_z,S_y$が垂直であることから0であるので、
$$k=\frac{S_x^TS_y}{S_y^TS_y}$$
となる。
見方を変えれば、自身との共分散は相関係数が常に1であり、それを分散と定義しているとも取れる。すなわち、共分散は自己相関のみで定義された分散という定義を相互相関に拡張したものだと言える。
一般化
さきほどまではサンプルX、Yを別々に定義していたが、前提にあるようにXとYを同時に得るような場合は以下の構造のサンプル行列Mを一つ定義すればすむ。
$$M=\left(\begin{array}{lcr}
x_1&y_1 \
x_2&y_2 \
x_3&y_3 \
x_4&y_4
\end{array}\right)$$
より一般的には、サンプルを構成する各データは$D$個ずつ得られるものとする。
それをD次元のベクトル$\mathbf w$として定義する。
n番目のデータは、
$$\mathbf w_n=(a_n,b_n,c_n,...)$$
で表現される。
サンプル行列$M$はこのとき、
$$M=(\mathbf w_1, \mathbf w_2,...,\mathbf w_N)$$
と定義できる。$M$はD行N列の行列とし、サンプルは列方向である。
このとき、偏差行列は$\mathbf w_n$をサンプル方向に平均した平均値ベクトル$\mu$を用いて、
$$S=M-\mu$$
と表せる。
※ただし、$\mu$は列(サンプル)方向に同じ値を使うしていくものとする。
相関は自己相関含めて2つの成分の組み合わせごとに計算できるので、分散と共分散はあわせてDxD個の組合せが存在する。
$$\Sigma=SS^T$$
ここで、$\Sigma$はD行D列の行列となる。その例として、
$$\Sigma_{ij}=\sum_nS_{in}S_{jn}$$
という風に、$i$次元目と$j$次元目の要素の共分散(対角成分は分散)が計算される。
この$\Sigma$のことを分散共分散行列という。
データの合成と主成分分析(PCA)
たとえば直交もしない、平行でない二つのベクトル$v,u$について、以下のような演算を行うことで直交するベクトルを取り出すことができる。
$$p=u|v|^2-(u\cdot v)v$$
こうすると、$v$と直交するように$u$を修正したベクトル$p$が得られる。$p$が$v$と直交することは両辺を$v$と内積をとればわかる。
ところで前述の議論で、サンプルの偏差$S_x,S_y$が直交しているかどうかで無相関かどうかが決まるという話があった。
もし現在のX,Yの間に相関をもつとすると、データの各成分を加算したりすることで無相関なサンプル2つP,Qに変換したら、P,Qはデータの解釈の助けにならないだろうか?
サンプルYに対して以下の修正を行おう。
$$P=(S_x^TS_x)Y-(S_x^T S_y)
X=V_xY-cov(x,y)X$$
線形変換なので偏差も同様に、
$$S_p=V_xS_y-cov(x,y)S_x$$
となる。
このとき、Xは変換をすることなく、Xと無相関となる合成サンプルPが得られた。
変換後の共分散を求めて、相関性をみよう。
$$cov(x,p)=S_x^TS_p=S_x^T(-cov(x,y)S_x+V_xS_y)$$
$$=(-cov(x,y)S_x^TS_x+V_xS_x^TS_y)=(-cov(x,y)V_x+V_xcov(x,y))=0$$
というわけで、めでたく無相関は達成した。
しかし、実はこの変換で無相関を実現すると、場合によって大きく情報を欠落することがある。
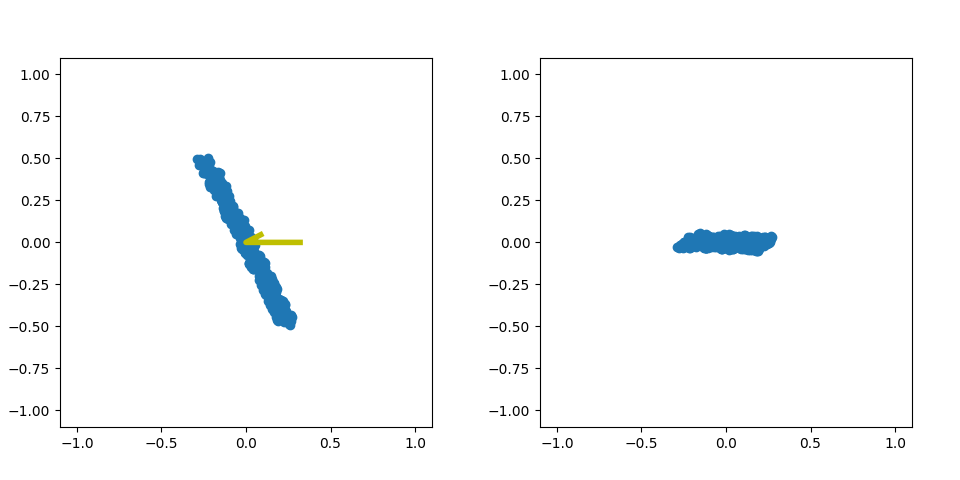
以下のグラフは、同じサンプルにおけるx-yとx-pの散布図だ。
x-pのグラフはp方向のばらつきがとても小さくなってしまっている。
なぜか?以下の二点が問題となっている。
- XとPがもとのデータの軸に対して直交しない軸への変換を行うと、データの一部情報が過小評価されたりする。
- スケールも変化しまっていることも、データの解釈を難しくしてしまう意味でまずい。
この二点を解決するような変換はつまり、
- 変換前の軸に対して、直交性を保つような軸への変換を行う。
- 変換前後でスケールを維持する
そして、これを満たしつつ
- サンプルを無相関となるような合成サンプルに変換する
を目指す。実に欲張りな用件で、そんな変換が実現できるのだろうか?答えをいえば、1通りだけ存在する。これを用いるものを主成分分析(PCA: principal component analysis)と呼ぶ。
ここからはX,Yをまとめて行列表記$M$で行おう。第一次目的はサンプル行列$M$の分散共分散行列$\Sigma=S_MS_M^T$を、
非対角成分(=次元間の共分散)を0にしてやれるような合成サンプル行列Pを作る方法がわかればいい。
合成サンプルは線形変換行列U(DxD次元の正方行列)を用いて、
$$P=U^TM$$
で定義される。つまり、Uが特定できれば第一目的は達成する。
Uを使って変換後の$\Sigma^U$を式で表そう。
$$\Sigma^U=S_US_U^T=U^TS_MS_M^TU=U^T\Sigma U$$
つまり、行列Uで元の分散共分散行列$\Sigma$を挟み込んで計算したとき、対角成分以外を0に落とすようなUを求めればいい。
なお、この操作は行列の対角化である。
これだけだとUは無数に存在するので、以下の二つの条件を追加で加える。
スケール不変かつ各軸が直交するように
$$U^TU=UU^T=I$$
この条件を満たす$U$のことをユニタリ行列という。なお、複素数を考慮したときは
$$U^\dagger U=UU^\dagger=I$$
となる($I$は単位行列)。$U^\dagger$は転置して複素共役をとること(=$U$のエルミート共役、随伴行列)とよぶ。
ユニタリ性をもつことで残り2条件を満たすことの証明は省略するが、簡単にいえばユニタリ行列は$U={u_i}$ ($u_i$はベクトル)としたとき、
$$(U^TU)={u_i^Tu_j}=I$$
つまり、構成するベクトル群$u_i$は長さが1であり、互いに直交するベクトルであると言える。このこの行列をベクトルに適用したときの役割は概ね座標の回転に対応する。
こうなるような行列は固有値固有ベクトルを用いることでできる。長さ1のベクトル$u$に対して固有値方程式
$$\Sigma \mathbf u=\lambda \mathbf u$$
を満たすようにするには
$$(\Sigma-\lambda I)u=0$$
なので、左辺の$\Sigma-\lambda I$の行列値が0である必要がある。それを解けば(行列式は$\lambda$に関してD次式になるため)重解含めてD個の値が求まる(固有値)。重解が存在しない場合はそれぞれ代入したときに不定方程式となるので、整理する。
たとえばD=2のとき、
$$au_x+bu_y=0$$
のように自由度1の関係式となる(a,bは変数ではなく値として求まる)。
このとき、$u=(b/r,-a/r), r=\sqrt(a^2+b^2)$となる、という感じで求まる。
まとめると、PCAは分散共分散行列を対角化するユニタリ行列を用いることで得られ、固有値固有ベクトルを求めればできる。ユニタリ行列は元のベクトルに対して作用させることは座標の回転になるので、
PCAは元のデータを無相関化させるような軸に回転させようとしたとき、各軸が向くべき方向を求める解析方法だといえる。
なお、無相関化した際に各成分の分散の大小が決まるが、大きいほどサンプルの情報をよく保持している軸だと言える。この分散は固有値に等しくなるので、固有値が大きい順に固有ベクトルをソートし、一定本数のベクトルを調べる使い方が一般的である。
一番固有値(=分散)が大きくなる軸を第一主成分という。
PCAの自力実装
では議論は終わったのでpythonにおいてnumpyだけでpcaを実装してみよう。
わざわざ実装しなくてもscikit-learnとかでpcaは使えるわけだが、結論から言えばわずか数行の関数を記述するだけでPCAは実装できるので、PCA使う為だけにわざわざscikit-learn依存にするのは冗長性が高いのではと思う(scikit-learn, 結構重いライブラリなので)。
PCAのテスト用サンプル
おそらく、コーディングに慣れた人ほど「コードは組むことよりテストする方が難しい」という考えを持っているだろう。
今回もそれに当てはまると思う。テストケースを考えるのは結構頭を使うし骨も折れる。
というわけで、まずはテストに適したサンプルを作っていこう。
PCAをテストしやすいサンプルとは、あらかじめ以下の式でランダムサンプリングすることで得られる。
$$w=a_1e_1+a_2e_2+a_3e_3$$
a,b,cは各々範囲を決めてランダムサンプルすることで得られ、$e_n$はXYZ軸を各軸まわりに適当に回転することで得られる。
適当に回転する操作は回転行列を3つ定義してやればできる。
例としてz軸周りの回転操作を行う回転行列は、
$$R_z=\left(\begin{array}{lcr}
\cos\theta&\sin\theta&0 \
-\sin\theta&\cos\theta&0 \
0&0&1
\end{array}\right)$$
x軸、y軸に対する回転行列もこれと同様に定義する。
せっかくなので$\theta$が面に見える表記で表すと、
$$J_z=\left(\begin{array}{lcr}
0&1&0 \
-1&0&0 \
0&0&0
\end{array}\right)
$$
なる$J_z$を用いて、
$$R_z=\exp(J_z\theta)$$
と表現できるのでこれを使おう。
なおこれは、
$$\exp(x)=\lim_{h\rightarrow 0}(1+xh)^\frac{1}{h}$$
と、微小回転行列
$$H=\left(\begin{array}{lcr}
1&h \
-h&1
\end{array}\right)$$
を知っていれば導くことは容易だろう(実装には意味ないが式が綺麗なので使う)。
ということで
$$E=(e_1,e_2,e_3)$$
という行列は、単位行列を各軸にそって適当に回転させれば得られるので、
$$E=\exp(J_x\theta_x)\exp(J_y\theta_y)\exp(J_z\theta_z)I$$
として定義できる。
ということで、PCRをテストしたいサンプルは、
- 単位行列を回転させる量$\theta_x,\theta_y,\theta_z$と、ランダムサンプルの値域$\sigma_a,\sigma_b,\sigma_c$を求める
- 回転後の軸$E$を求める。
- N個の(a,b,c)を範囲$[0,k_a],[0,k,b],[0,k_c]$の一様分布からサンプリングする。なお簡単のために$k_a>k_b>k_c$としておく。
とすることで得られる。
得たサンプルをPCAして得られる各単位ベクトルは、第一主成分から順に:
$$(e_a,e_b,e_c)$$
であることが期待値となる。
また、各ベクトルに対する分散期待値は、
$$(\frac{k_x^2}{12},\frac{k_y^2}{12},\frac{k_z^2}{12})$$
であることが期待値となることは以下の式から分かる。
$$\int_0^1 k^2(x-\frac{1}{2})^2dx=\frac{k^2}{12}$$
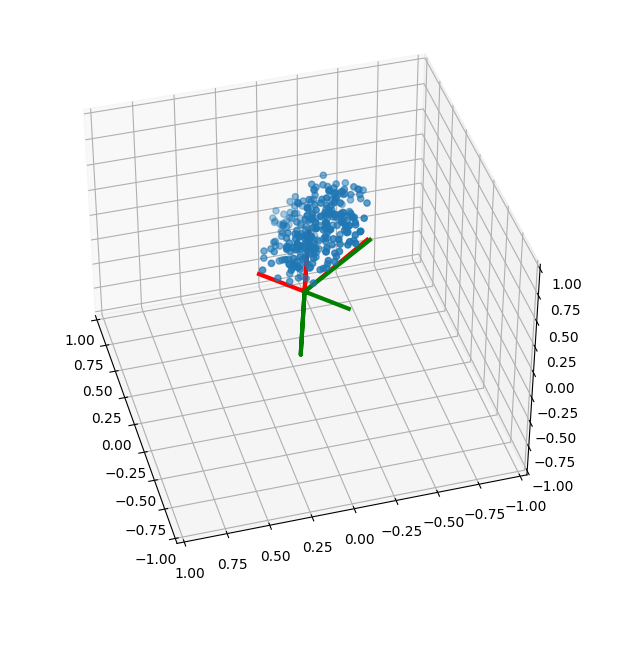
例として、3d空間上にランダムな相関性を持つサンプルを作ってみよう。pythonで書くと以下。
def makerotmat(tX,tY,tZ):
# create rotation matrices corresponding to rotations about each axis.
zrot=np.array([[np.cos(tZ),-np.sin(tZ),0],[np.sin(tZ),np.cos(tZ),0],[0,0,1]])
yrot=np.array([[np.cos(tY),0,-np.sin(tY)],[0,1,0],[np.sin(tY),0,np.cos(tY)]])
xrot=np.array([[1,0,0],[0,np.cos(tX),-np.sin(tX)],[0,np.sin(tX),np.cos(tX)]])
return xrot,yrot,zrot
def rotateVec(tX,tY,tZ,m):
# calc m -> exp(Jx.tX)exp(Jy.tY)exp(Jz.tZ)m
xr,yr,zr=makerotmat(tX,tY,tZ)
m=(zr@(yr@(xr@m)))
return m
def make_sample3d(rots=None, scales=None, num=300):
# random rotation and rescaling.
# make random-axes to do it.
if rots is None:
rots=np.random.uniform(size=(3,))*2*np.pi
if scales is None:
scales=0.1+np.random.uniform(size=(3,))*0.7
scales.sort()
scales=scales[::-1]
# generate uncorrelated random 3d-data.
seed=np.random.uniform(size=(3,num))*scales[:,None]
# ideal variance of this distribution.
eig_val_gt=np.array(scales)**2/12
# unit vector of xyz-axis.
xyz_axes=np.array([[1,0,0],[0,1,0],[0,0,1]])
# make ground truth of unitary matrix.
unitary_gt=rotateVec(*rots,xyz_axes)
# rotate the data.
data=unitary_gt@seed
return data, (eig_val_gt, unitary_gt)
作った関数をmatplotlibでテストしよう。
import matplotlib.pyplot as plt
data, (eigval_gt, unitary_gt)=make_sample3d()
fig=plt.figure()
ax=fig.add_subplot(1,1,1,projection="3d")
ax.set_xlim(-1,1)
ax.set_ylim(-1,1)
ax.set_zlim(-1,1)
ax.scatter(*data)
drawaxes(ax, unitary_gt, eigval_gt, "r", 3)
plt.show()
本来、1つだけの場合はsubplotを使う必要はないのだが、subplotでない場合の書き方を忘れたのでこのままにする(適当)
drawaxes関数はユニタリ行列と固有値を入力したら、一様分布を仮定したときの各軸の長さを描画する関数として定義する。
def drawaxes(sp, axes, eigvals, color, lw):
es=(eigvals*3*4)**(1/2)
axes=(axes*es[None,:])
vax=np.concatenate((axes, axes*0), axis=1)
if axes.shape[0]==2:
vax=vax[:,(0,2,1)]
else:
vax=vax[:,(0,3,1,3,2)]
sp.plot(*vax, color=color, lw=lw)
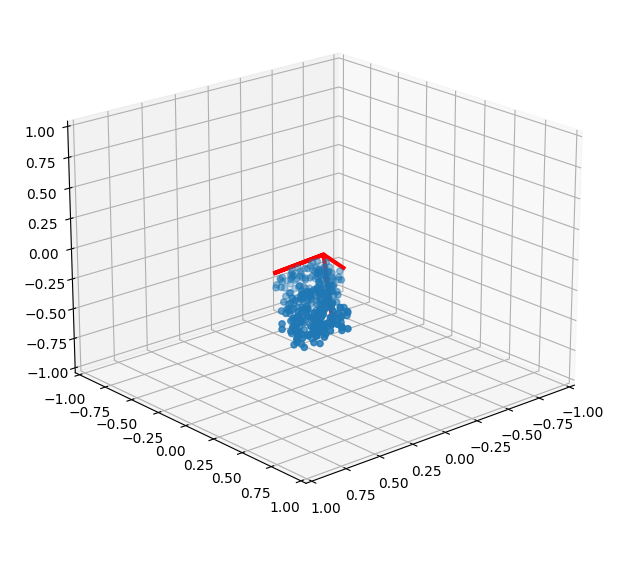
うまい具合にX軸、Y軸、Z軸それぞれで相互相関性をもってくれているように見える。赤い線は一様分布からサンプリングしてきた各軸を意味する。固有値から長さも正しく復元できているようだ。
PCA本体の実装
これは、先ほど議論したPCAの考え方を踏襲して実装すれば、それほど難しくない。
念のため手順をおさらいしよう。
- サンプルの分散共分散行列$\Sigma$を求める
- $\Sigma$の固有値固有ベクトルを求める
- 固有値が大きい順にソートする
なお、固有値は座標変換値の各軸の分散に対応するので0以上は保証されると言っていいはずだ。
手順通りに組むと以下になる。
# calc variance-covariance matrix.
def CalcSigma(data):
sd=data-data.mean(axis=1)[:,None]
Sigma=(sd@sd.T)/sd.shape[1]
return sd, Sigma
# calc pca.
def pca(data):
_, Sigma=CalcSigma(data)
ew, rvec=np.linalg.eig(Sigma)
ewi=np.argsort(ew)[::-1]
ew=ew[ewi]
rvec=rvec[:,ewi]
unitary=rvec
return ew, unitary
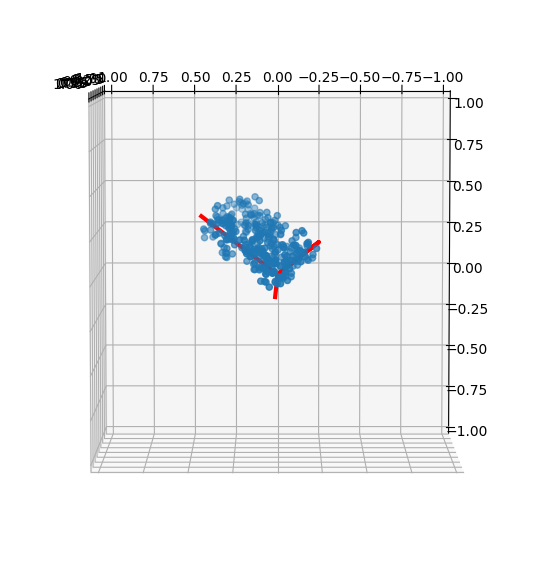
さて、組んだコードを実行し、
各サンプルのPCAした結果の期待値と比較しよう。
なお、PCAで得られた軸は元々乱数で使った軸とは反対になることがあるが、PCAは平均値からの分散方向を求めていることにある。平均$\bar x$に対して、偏差のサンプリング$r\in[-0.5,0.5]$に対して$x=\bar x+re_r$でサンプリングしたのか、$x=\bar x-re_r$でサンプリングしたのかの区別が付かないことによる。
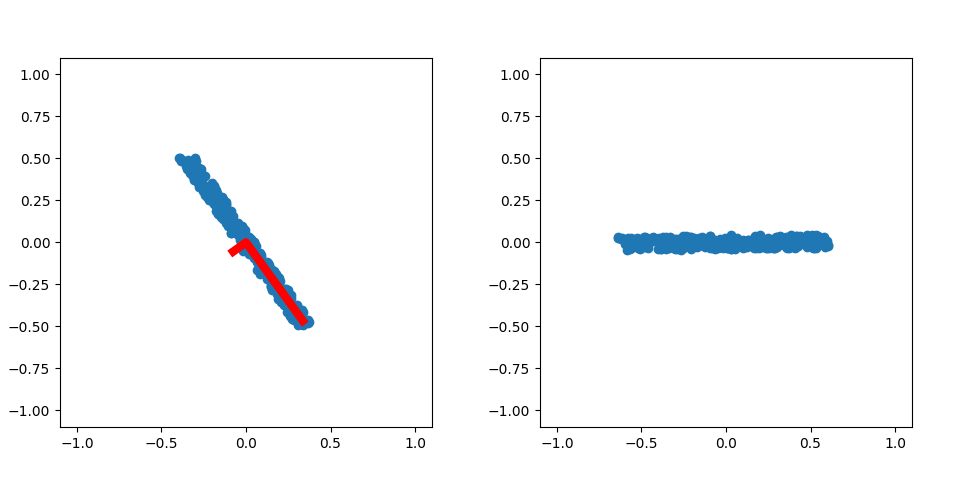
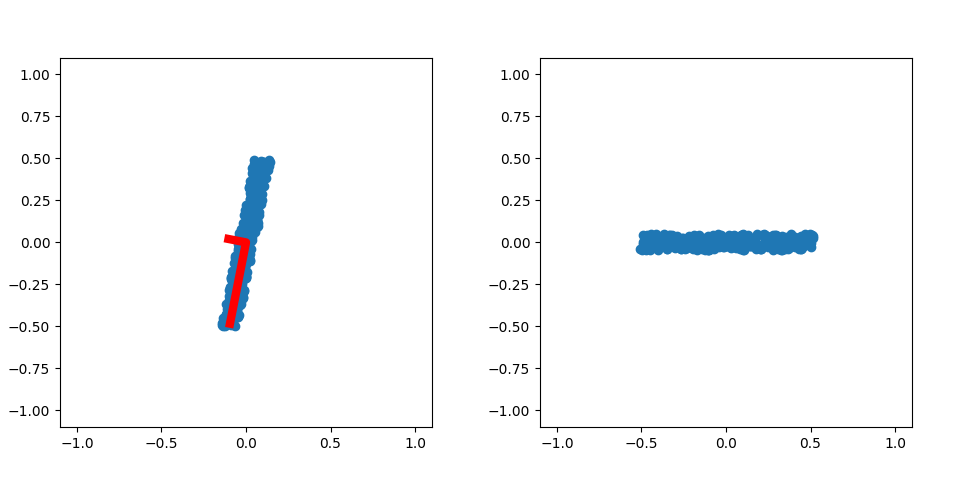
この図は軸の描画をサンプリングの一辺から伸ばしていることが問題なようだ。
軸をサンプリングの重心から片方向の範囲分をのばすようにしよう。そのとき3d図だとわかりにくいので、2dの場合のテストで行う。
左の図は、サンプルに対してPCAして得られた各軸を固有値で一様分布の範囲まで伸ばした線を赤線で描いている。
図の右側は赤線の軸に沿ってサンプルを回転させたものだ。右図の分布が縦横で斜めに関係を持っていないので無相関であることは分かる。
数値上で手っ取り早く確認したい場合は、
e,u=pca(data)
u_data=u.T@data
s=u_data-u_data.mean(axis=1)[:,None]
Sigma=s@s.T/s.shape[1]
として、ユニタリ行列を逆回転させたデータで分散共分散行列を求め、対角成分以外が非常に小さい値になっているか確認すればよい。
所感
共分散のおさらいから、PCAの実装までをしてみたら以外と長い記事になってしまった。イチからまとめることで理解が整理されたのはよかったかなと思う。