目次
概要
既に以下の記事を読んでいることを前提とします。
【プログラマーのための統計学】 度数分布とヒストグラム
ローレンツ曲線とは
所得や、人口の偏りなどを調べるために作成するグラフのことです。
例として、ある地域の村の人口の偏りを調査します。
村の数は全部で100とします。
各村の人口は以下のようになりました。
見辛いですが、全ての村の全人口をlistにしてあります。
population = [
124, 151, 102, 189, 160, 145, 120, 132, 135, 159, 114, 175, 171, 124, 154,
177, 152, 120, 144, 121, 113, 163, 186, 196, 183, 105, 130, 149, 130, 123,
175, 143, 186, 182, 184, 174, 134, 158, 196, 109,
216, 285, 209, 288, 276, 281, 283, 200, 262,
267, 235, 206, 245, 232, 299, 249, 295, 232, 206, 237,
369,
487, 450, 487,
597, 548,
682,
712, 706, 755, 700, 709, 747, 773, 796, 739, 716, 756, 767, 752, 728, 750,
829, 875, 845, 881, 865, 804, 845, 890, 872, 833, 874, 845, 859, 837, 847, 811, 893, 807
]
ローレンツ曲線を求めるには
ローレンツ曲線は、X軸、Y軸に、それぞれ2種類の累積相対度数が必要になります。
- 各階級の度数の累積相対度数
- 各階級に属する値の合計の累積相対度数
それぞれ説明をしていきます。
1. 各階級の度数の累積相対度数
まず1つ目は、階級を人口、度数を村の数とした、累積相対度数を算出します。
こちらの記事に書いた内容と同じ要領で、計算をします。
【プログラマーのための統計学】 度数分布とヒストグラム
| 階級 | 階級値 | 度数 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| 100人以上 - 200人未満 | 150 | 40 | 0.40 | 0.40 |
| 200人以上 - 300人未満 | 250 | 20 | 0.20 | 0.60 |
| 300人以上 - 400人未満 | 350 | 1 | 0.01 | 0.61 |
| 400人以上 - 500人未満 | 450 | 3 | 0.03 | 0.64 |
| 500人以上 - 600人未満 | 550 | 2 | 0.02 | 0.66 |
| 600人以上 - 700人未満 | 650 | 1 | 0.01 | 0.67 |
| 700人以上 - 800人未満 | 750 | 15 | 0.15 | 0.82 |
| 800人以上 - 900人未満 | 850 | 18 | 0.18 | 1.00 |
2. 各階級に属する値の合計の累積相対度数
2つ目は、階級を人口、度数を各階級ごとの村の合計人数とした、累積相対度数を算出します。
各階級ごとの村の合計人数を出すために、前述のpopulationという名前の変数のlistの値を元に計算します。
例えば、「400人以上 - 500人未満」の合計人数は、下記のように、1424人になります。
1424 = 487 + 450 + 487
また、全ての村の人口の合計は41029人になるので(populationの値を全て足した値)、相対度数は、
「400人以上 - 500人未満」の場合は、0.03(小数点第3位以下切り捨て)となります。
0.03 = \frac{1424}{41029}
このような形で各階級を計算し、人数の累積相対度数を算出します。
度数分布表
前述の1つ目、2つ目をまとめた度数分布表です。
(相対度数、累積相対度数は、小数点第3位以下は切り捨てています)
| 階級 | 階級値 | 度数 | 相対度数 | 度数の累積相対度数 | 合計人数(度数) | 人数の相対度数 | 人数の累積相対度数 |
|---|---|---|---|---|---|---|---|
| 100人以上 - 200人未満 | 150 | 40 | 0.40 | 0.40 | 5988 | 0.14 | 0.15 |
| 200人以上 - 300人未満 | 250 | 20 | 0.20 | 0.60 | 5003 | 0.12 | 0.27 |
| 300人以上 - 400人未満 | 350 | 1 | 0.01 | 0.61 | 369 | 0.01 | 0.28 |
| 400人以上 - 500人未満 | 450 | 3 | 0.03 | 0.64 | 1424 | 0.03 | 0.31 |
| 500人以上 - 600人未満 | 550 | 2 | 0.02 | 0.66 | 1145 | 0.02 | 0.34 |
| 600人以上 - 700人未満 | 650 | 1 | 0.01 | 0.67 | 682 | 0.01 | 0.36 |
| 700人以上 - 800人未満 | 750 | 15 | 0.15 | 0.82 | 11106 | 0.27 | 0.63 |
| 800人以上 - 900人未満 | 850 | 18 | 0.18 | 1.00 | 15312 | 0.37 | 1.00 |
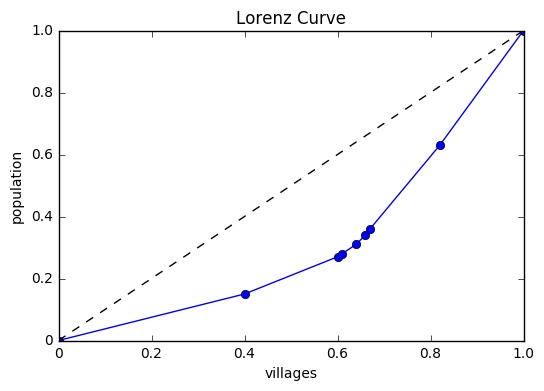
この表の「度数の累積相対度数」をx軸、「人数の累積相対度数」をy軸にしたグラフが、ローレンツ曲線になります。
ローレンツ曲線を描く
前述のデータを、matplotlibを使って、グラフにします。
参考:jupyter(ipython notebook) + matplotlib + vagrantでグラフ描画
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
# 横座標, 度数の累積相対度数
left = np.array([
0,
0.40,
0.60,
0.61,
0.64,
0.66,
0.67,
0.82,
1.00,
])
# 縦座標, 人数の累積相対度数
height = np.array([
0,
0.15,
0.27,
0.28,
0.31,
0.34,
0.36,
0.63,
1.00
])
ax.plot(left, height, marker='o')
# グラフのタイトル
plt.title('Lorenz Curve')
# X軸のタイトル
plt.xlabel('villages')
# Y軸のタイトル
plt.ylabel('population')
left = np.array([0, 0.2, 0.4, 0.6, 0.8, 1.0])
height = np.array([0, 0.2, 0.4, 0.6, 0.8, 1.0])
ax.plot(left, height, linestyle='dashed', color='black')
# X軸のラベル
label = [0, 0.2, 0.4, 0.6, 0.8, 1.0]
# ラベルを打つX軸の場所
ax.set_xticks(label)
# X軸にラベルをセット
ax.set_xticklabels(label)
# ラベルを打つY軸の場所
ax.set_yticks(label)
# Y軸にラベルをセット
ax.set_yticklabels(label)
# 描画
plt.show()
この青い曲線が、ローレンツ曲線です。
ローレンツ曲線を見て分かること
上記で作成したローレンツ曲線を、どのように見ればよいのかを説明します。
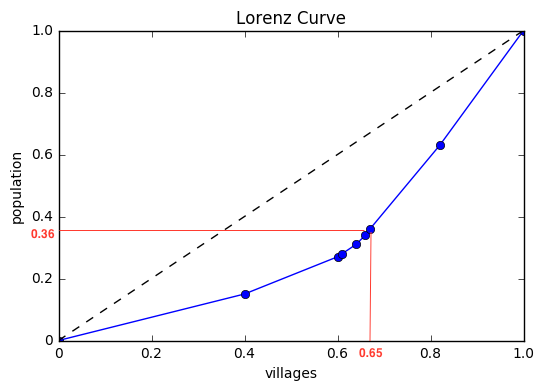
赤線を引いた部分の座標を見てみます。
この点からわかることは、約65%の村が、全人口の36%くらいしかいないということです。
つまり、残り64%の人口は、他のどこかの村に偏っているということになります。
また、曲線の膨らみが大きいほど、偏りがあるということになります。
ジニ係数
この偏りを数値で表したものを、ジニ係数といいます。
ジニ係数の出し方ですが、まず、上記グラフの破線を「完全平等線」といいます。
この「完全平等線」と、ローレンツ曲線の間の面積を2倍したものが、ジニ係数になります。
ジニ係数は0から1までの値をとなり、1に近くほど偏りが大きく、0に近くほど偏りが少ないということになります。
ちなみに、ジニ係数が0の場合は、ローレンツ曲線は、完全平等線と重なります。
ジニ係数を算出する
実際にジニ係数を計算します。
ここでは、計算をしやすいように、前述の例ではなく、以下の値を使って計算します。
X軸
0, 0.4, 0.8, 1
Y軸
0, 0.2, 0.6, 1.0
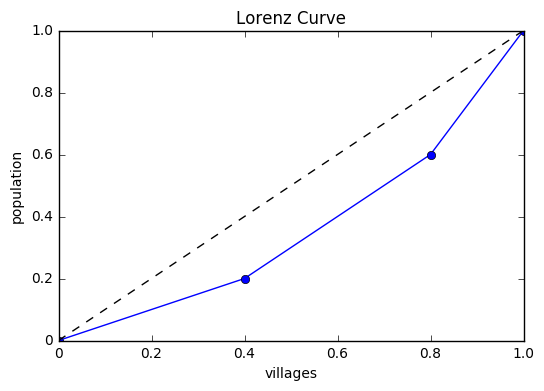
この値から、以下のようなローレンツ曲線が出来上がります。
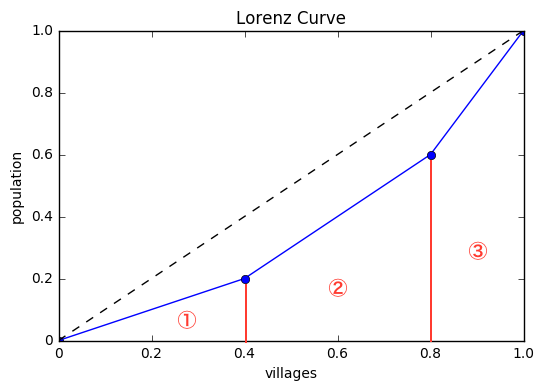
このグラフを、以下のように分割して、完全平等線を斜辺とした三角形から、図の、1、2、3の部分の面積を引いて2倍すれば、ジニ係数が求められます。
まず、完全平等線を斜辺とした三角形の面積を求めます。
0.5 = 1\times1\div2
1の部分の面積を求めます。
底辺が0.4、高さが0.2の直角三角形なので、以下で求められます。
0.04 = 0.4\times0.2\div2
2の部分の面積を求めます。
右に回転させると、上底0.2, 下底0.6, 高さ0.4の台形となるので、以下で求められます。
0.16 = (0.2+0.6)\times0.4\div2
3の部分の面積を求めます。
こちらも右に回転させると、上底0.6, 下底1, 高さ0.2の台形となるので、以下で求められます。
0.16 = (0.6+1)\times0.2\div2
これらを3つの値を、完全平等線を斜辺とした三角形の面積から引いて、2倍すればジニ係数が出るので、下記の式のとおり、0.28がジニ係数となります。
0.28 = (0.5 - 0.04 - 0.16 - 0.16)\times2
以上