目次
概要
統計学で使用する、度数分布とヒストグラムについてです。
pythonでヒストグラムを作成もします。
度数分布
度数分布とは
収集したデータをいくつかの階級(区間)に分けたときの、それぞれの階級に所属するデータの分布状況のこと
引用元:コトバンク
らしいです。言葉の定義だけでは難しいので、実際に例を挙げて説明していきます。
度数分布表
ある組織の年齢の分布を調べるとします。
組織の人数は全部で100人いるとします。
調査した結果、下記のような結果になりました。
非常に見づらいですが、100人全員分の年齢をlistにしています。
ages = [23, 22, 23, 22, 24, 20, 22, 24,
29, 28, 25, 25, 26, 27, 28, 27, 25, 25, 27, 25, 25,
32, 32, 32, 33, 33, 32, 33, 32, 30, 33, 32,
35, 39, 38, 38, 37, 35, 38, 35, 35, 38, 35, 37,
43, 44, 40, 41, 44, 41, 40, 43, 44, 41, 41, 44, 43, 42, 40, 44, 42, 41, 42,
47, 49, 49, 46, 48, 45, 49, 49, 49, 49, 49, 48, 46, 49, 45, 48, 49, 48,
54, 52, 54, 53, 53, 54, 50, 51, 52, 54,
58, 56, 58, 58, 55, 57, 56, 56, 55]
このデータを元に、年齢層別の分布表を作ります。
このような表のことを、度数分布表と言います。
| 階級 | 階級値 | 度数 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| 20歳以上 - 25歳未満 | 22.5 | 8人 | 0.08 | 0.08 |
| 25歳以上 - 30歳未満 | 27.5 | 13人 | 0.13 | 0.21 |
| 30歳以上 - 35歳未満 | 32.5 | 11人 | 0.11 | 0.32 |
| 35歳以上 - 40歳未満 | 37.5 | 12人 | 0.12 | 0.44 |
| 40歳以上 - 45歳未満 | 42.5 | 19人 | 0.19 | 0.63 |
| 45歳以上 - 50歳未満 | 47.5 | 18人 | 0.18 | 0.81 |
| 50歳以上 - 55歳未満 | 52.5 | 10人 | 0.10 | 0.91 |
| 55歳以上 - 60歳未満 | 57.5 | 9人 | 0.09 | 1.00 |
以下、各項目の説明です。
[階級]
度数を集計するためのグループ分けした区間。この例では年齢。
[階級値]
階級の真ん中の値のこと。
階級がa以上b未満のとき、階級値は以下で求められます。
階級値 = \frac{a+b}{2}
上記の表の20歳以上25歳未満の場合の階級値は、22.5になります。
22.5 = \frac{20+25}{2}
[度数]
該当の階級のデータ数。この例では、人数。
[相対度数]
各階級ごとの度数の全体に占める割合で、度数 / 合計 。
相対度数 = \frac{度数}{合計}
この例では、 各階級の人数 / 100人 となるので、上記の表の20歳以上25歳未満の場合の相対度数は 0.08 になります。
0.08 = \frac{8}{100}
[累積相対度数]
その階級までの相対度数の全ての和(累積和)のことです。
上記の表の場合は、以下のようになります。
20歳以上 - 25歳未満 = 0.08
25歳以上 - 30歳未満 = 0.08 + 0.13
30歳以上 - 35歳未満 = 0.08 + 0.13 + 0.11
35歳以上 - 40歳未満 = 0.08 + 0.13 + 0.11 + 0.12
︙
55歳以上 - 60歳未満 = 0.08 + 0.13 + 0.11 + 0.12 + 0.19 + 0.18 + 0.1 + 0.09 = 1
一番最後の階級は必ず 1 になります。
ヒストグラム
ヒストグラムとは度数分布表をグラフにしたもののことです。
前述の度数分布表を、pythonのmatplotlibを使って、ヒストグラムにします。
(正しくは、ヒストグラムに見せかけた棒グラフを作ります。詳細は後述します。)
matplotlibの使い方はこちらを参照
jupyter(ipython notebook) + matplotlib + vagrantでグラフ描画
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
# 横座標
left = np.array([0, 1, 2, 3, 4, 5, 6, 7])
# 縦座標
height = np.array([8, 13, 11, 12, 19, 18, 10, 9])
ax.bar(left, height, width=1.0)
# グラフのタイトル
plt.title('Ages')
# X軸のタイトル
plt.xlabel('Age group')
# Y軸のタイトル
plt.ylabel('Numbers')
# X軸のラベル
label = [
'20 - 24',
'25 - 29',
'30 - 34',
'35 - 39',
'40 - 44',
'45 - 49',
'50 - 54',
'55 - 59'
]
# ラベルを打つX軸の場所
ax.set_xticks([0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5])
# X軸にラベルをセット、90度回転させる
ax.set_xticklabels(label, rotation = 90)
# 描画
plt.show()
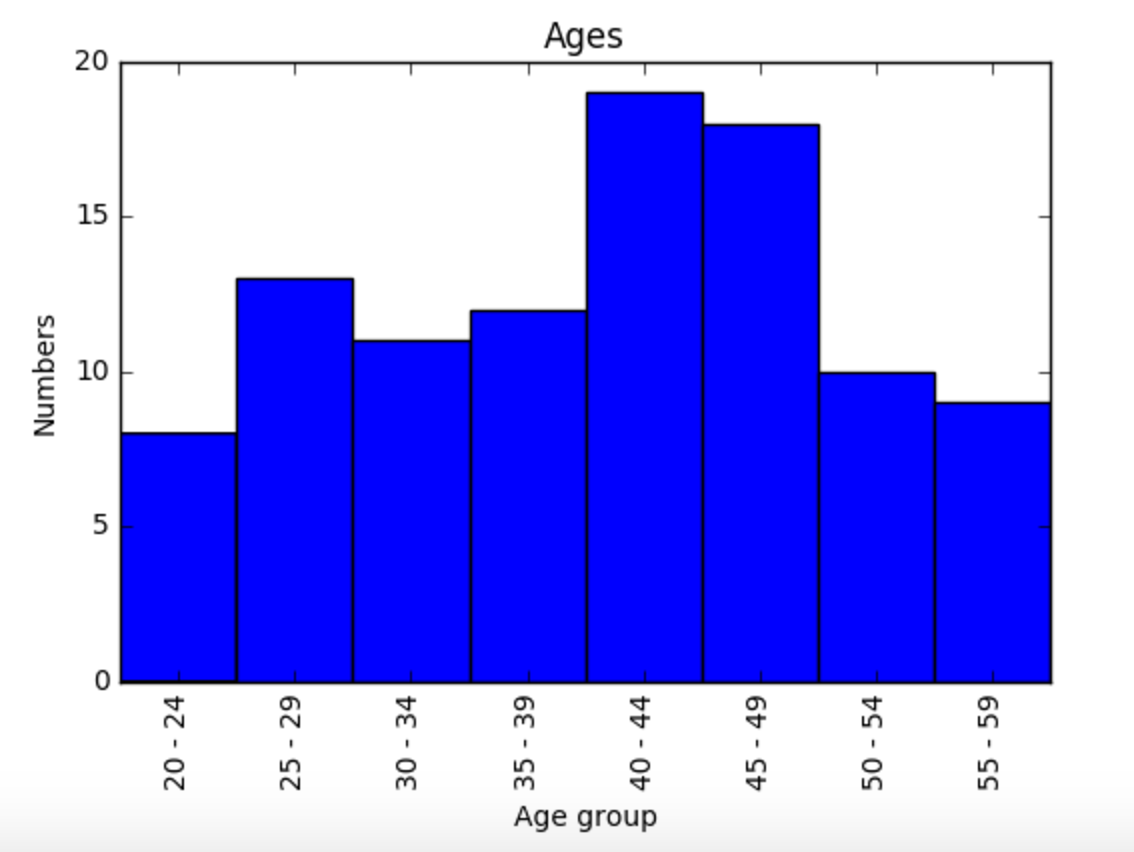
すると、このようなグラフが出来上がります。
これが、ヒストグラムです。

X軸が階級(年齢層)、Y軸は度数(人数)を表しています。
40歳以上 - 45歳未満が一番多いことがわかります。
ヒストグラムと棒グラフ
ヒストグラムは棒グラフに見えますが、厳密には、ヒストグラムと棒グラフは違います。
■棒グラフ
棒:それぞれが独立している
軸:お好きに、どうぞ
使う目的:棒同士を比較する
■ヒストグラム
棒:全部でひとつ
軸:横軸が「階級」で縦軸が「度数」
使う目的:分布を見る
らしいです。
詳細は下記を参照してください。
「棒グラフ」と「ヒストグラム」の違い
pythonのmatplotlibを使ってヒストグラムを作る
先ほど、「ヒストグラムに見せかけた棒グラフを作ります。」と言いましたが、
今度は、matplotlibを使って、本当のヒストグラムを作成します。
前述の例では、集計結果を度数分布表にしてから、ヒストグラム(実際は棒グラフ)を作りました。
しかし、pythonのmatplotlibを使えば、集計結果からそのままヒストグラムを作ることができます。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# 100人分の年齢
ages = [
23, 22, 23, 22, 24, 20, 22, 24,
29, 28, 25, 25, 26, 27, 28, 27, 25, 25, 27, 25, 25,
32, 32, 32, 33, 33, 32, 33, 32, 30, 33, 32,
35, 39, 38, 38, 37, 35, 38, 35, 35, 38, 35, 37,
43, 44, 40, 41, 44, 41, 40, 43, 44, 41, 41, 44, 43, 42, 40, 44, 42, 41, 42,
47, 49, 49, 46, 48, 45, 49, 49, 49, 49, 49, 48, 46, 49, 45, 48, 49, 48,
54, 52, 54, 53, 53, 54, 50, 51, 52, 54,
58, 56, 58, 58, 55, 57, 56, 56, 55]
fig, ax = plt.subplots()
# 8個の階級でヒストグラムを作成します。binsの最小値と最大値をrangeで指定します。
# 戻り値について n => 各階級における度数、bins => 階級のリスト
n, bins, patches = ax.hist(ages, bins=8, range=(20, 60))
# グラフのタイトル
ax.set_title('Ages')
# X軸のタイトル
ax.set_xlabel('Age group')
# Y軸のタイトル
ax.set_ylabel('Numbers')
# X軸のラベル
label = [
'20 - 24',
'25 - 29',
'30 - 34',
'35 - 39',
'40 - 44',
'45 - 49',
'50 - 54',
'55 - 59'
]
# ラベルを打つX軸の場所。階級値をセットする。
ax.set_xticks([22.5, 27.5, 32.5, 37.5, 42.5, 47.5, 52.5, 57.5])
# X軸にラベルをセット、90度回転させる
ax.set_xticklabels(label, rotation = 90)
# 描画
plt.show()
これを実行すると、先ほど棒グラフとして作成したものと、同じ形のヒストグラムが出来上がりました!
度数分布表を作成しなくてよいので、とても便利ですね!
階級幅の決め方
階級の幅の決め方ですが、特にルールがあるわけではありませんが、
スタージェスの公式を使って算出するということもできます。
k=1+log_2N
n はデータ数、k は階級数になります。
前述の例だと、k は100になり、以下のようになります。
k=1+log_2100
log2 というのは自然対数です。
参考:2の自然対数
なんか難しそうですが、
pythonであれば、以下の関数で求めることができます。
python2系の場合
import math
k = 1 + math.log(n, 2)
python3系の場合
import math
k = 1 + math.log2(n)
ただし、スタージェスの公式で求められる値は、あくまで目安なので、階級数が明確な場合は、わざわざ公式を使う必要はありません。
次項:ローレンツ曲線とジニ係数