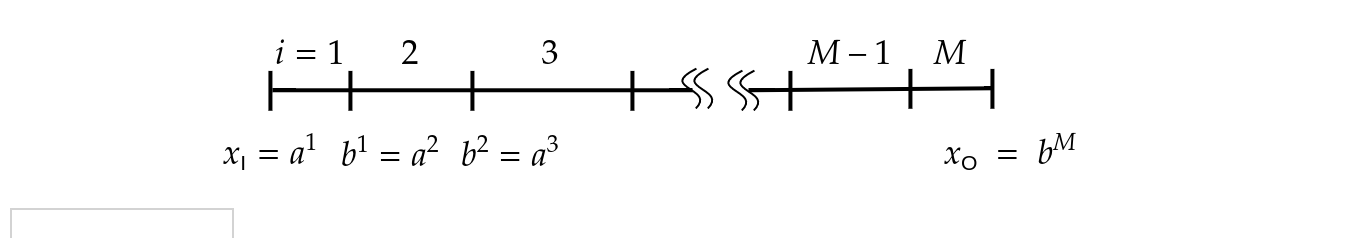スペクトル要素法事始：Chebyshev多項式を用いて一次元Helmholtz方程式を解く

スペクトル要素法：有限要素法とスペクトル法を通じた理解

TwitterではRunge-Kuttaに続いて有限要素法が流行っていますが，2018年の数値計算Advent calendarにもいくつか有限要素法を扱った記事がありました．

• @nqomorita さんの記事「有限要素法と反復法線形ソルバのはじめの一歩 [前編]」では，熱伝導方程式を題材に有限要素法の離散化がとてもわかりやすく解説されています．
• @t_kemmochi さんの記事「FreeFem++の紹介」はとてつもない大作で，有限要素法を用いた偏微分方程式の解析ソフトであるFeeeFem++のきわめて充実したチュートリアルとmatplotlibを用いた可視化，さらには付録として関数解析を用いた有限要素法の理論的な解説までがまとめられています．
• @muripo_life さんの記事「Galerkin法の数理についてまとめてみた」では，有限要素法で広く用いられるGalerkin法について，関数解析まで踏み込んでの解説がまとめられています．

有限要素法とは 弱形式（積分形式）で定式化した支配方程式を領域を分割した「要素」ごとに基底関数で展開し，線形の行列方程式を構成して解く手法です．領域を要素に分割するため複雑な形状に対応でき，現実世界での様々な問題を解く際にきわめて強力です．しかしながら，基底関数が低次のため精度に限界があるという欠点があります．¹
それに対し，スペクトル法と呼ばれる方程式に現れる物理量を高次の展開関数で近似して計算する手法は，有限要素法とある種相補的な性質を持ちます．つまり，領域全体を一つの展開関数で記述するため領域の形状や境界条件に制限が生じる代わりに，展開関数の次数を上げることで精度を飛躍的に向上させることができます．ごく簡単にまとめると，

• 有限要素法は領域を要素に分割するためさまざまな領域形状で問題を解くことができるが，展開関数が低次のため（スペクトル法に比べると）精度が良くない
• スペクトル法は高次の展開関数を用いるため高精度だが，領域全体で一つの展開関数を用いるため領域の形状などに対し制限を抱える

といえます．²

[](
スペクトル法の中でも最も一般的なのは展開関数として三角関数を用いるFourierスペクトル法で，この手法は系が周期性をもつことを要請します．

	スペクトル法	有限要素法
基底関数	高次（三角関数，Chebyshev多項式など）	線形
領域形状	特殊（周期境界条件など）	任意
)

そこで，これらの手法を組み合わせて 複雑な領域にも対応できる一般性をもち，しかも精度の良い手法 が欲しくなります．この手法こそが今回紹介する スペクトル要素法 です．スペクトル法あるいは有限要素法をご存じの方にとっては，

• 有限要素法から見ると，各要素の基底関数としてより高次（かつ性質の良いもの）を用いる
• スペクトル法から見ると，領域を要素に分割した上で弱形式の支配方程式にスペクトル法を適用し，要素境界には弱形式による連続性を用いる

と書くと理解しやすいと思います．

---

この記事では，スペクトル要素法が初めて提唱された1984年の論文
A spectral element method for fluid dynamics: Laminar flow in a channel expansion
の1.3節に基づいて，Dirichlet境界条件のもとでの一次元Helmholtz方程式

\begin{align}
\left\{ \begin{array}{l}
  \frac{\mathrm{d}^2 u(x)}{\mathrm{d} x^2} -\lambda^2 u(x) = f(x), ~~~~~-1 \le x \le 1 \\
  u(-1) = u(1) = 0 \\
\end{array} \right.
\end{align}

を解くプログラムをJuliaで実装し，スペクトル要素法の一端を紹介したいと思います．³

スペクトル要素法のアルゴリズム

領域の要素分割

一次元領域 $[x_{\text{I}}, x_{\text{O}}]$ を $M$ の要素に分割し， $i$ 番目の要素を $N_{x}^{i}+1$ の離散点で補間することを考えます．
各要素が $x^i \in [a^i, b^i]$ の領域を担当するものとして，

\begin{align}
  [x_{\text{I}}, x_{\text{O}}] &= [a^1, b^1] \cup [a^2, b^2] \cup \cdots \cup [a^i, b^i] \cup \cdots \cup [a^M, b^M] \nonumber \\
  &= \bigcup_{i=1}^{M} [a^i, b^i], ~~~~~~~~(a^1 = x_{\text{I}}, b^M = x_{\text{O}})
\end{align}

のようにします．

[](
この様子を示す．
$i$番領域の開始点$a^i$は，「領域開始点$+(i-1)$番要素が覆う距離」として定義できる．
いま，各要素について$[a^i, b^i]$は必ずしも等しくない．
これを$L^i$と書くことにする．

\begin{align}
  a^i &= a^1 +\sum_{j=1}^{i-1} (b^j -a^j) \nonumber \\
      &= a^1 +\sum_{j=1}^{i-1} L^j
\end{align}

大域座標を$M$の要素に「等分する」とすると，$L^i$をより直観的に書くことができる．

\begin{align}
  L^i &= \frac{x_{\text{O}} -x_{\text{I}}}{M} \nonumber \\
      &= \frac{b^M -a^1}{M}
\end{align}

このときEq. \ref{eq:Defofai}をより明示的に書くことができる．

\begin{align}
  a^i &= x_{\text{I}} +\sum_{j=1}^{i-1} L^j \nonumber \\
      &= a^1 +(i-1) \frac{b^M -a^1}{M} \nonumber \\
      &= \Big( 1-\frac{i-1}{M} \Big) a^1 +\frac{i-1}{M} b^M
\end{align}

これで，大域座標を$M$この自由な要素に分割することができた．
)
いま，ある要素を「大域座標」 $x \in [a^i, b^i]$ から「局所座標」 $\bar{x}^i \in [-1,1]$ に写すような写像を考えられます．
この局所座標を $\cos$ を用いて $N_{x}^i+1$ 点に離散化すると，

  \bar{x}_{j}^i = \cos \frac{\pi j}{N_{x}^i}, ~~~(j = 0, 1, \dots N_{x}^i)

のように書けます．

局所座標における離散点 $\bar{x}^i_j \in [-1,1]$ と，対応する大域座標 $x_q \in [a^i, b^i]$ には 要素境界のオーバーラップを除いて 一対一の関係があります．

[](

  \bar{x}_{j}^i = \frac{2}{L^i} (x_{q}-a^i) -1

ただし，両座標の定義域について以下のように確かめられる．

\begin{align}
  x &\in [a^i, a^i+L^i] \\
  x-a^i &\in [0, L^i] \\
  \frac{1}{L^i} (x-a^i) &\in [0,1] \\
  \frac{2}{L^i} (x-a^i) &\in [0,2] \\
  \therefore \frac{2}{L^i} (x-a^i)-1 &\in [-1,1].
\end{align}

Eq. \ref{eq:ConnectLocalGlobalCoordinate}を離散点で表す．

  \bar{x}_{j}^i = \frac{2}{L^i} (x_{q}-a^i) -1

ただし大域座標のナンバリング$q$は次式で定義される．

  q = \sum_{l=1}^{i-1} N_{x}^{l} +j

これは，大域座標で考える$i$番要素の$N_{x}^i$番座標$\bar{x}{N{x}^i}^i$と$i+1$番要素の$0$番座標$\bar{x}_{0}^{i+1}$が重なることによる．

  \bar{x}_{N_{x}^i}^i = \bar{x}_{0}^{i+1}

また，Eq. \ref{eq:DefofqofGlobalCoordinate}について，離散点数$N_{x}^i$が全ての要素で相等しいとき，これを$N_x$としてより簡単に$q$を表せる．

  q = (i-1) N_x +j

ここで，全離散点数$N_{x}^\text{all}$を定義しておく．

\begin{align}
  N_{x}^\text{all} &= \sum_{l=1}^{M} N_{x}^{l} +1 \\
                   &= M N_{x} +1 ~~~(\text{only if } N_{x}^i \text{ is always equal} )
\end{align}

)

Chebyshev多項式と物理量の近似

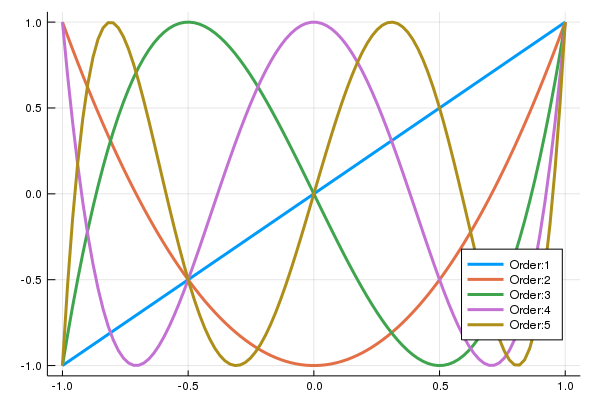
Chebyshev多項式は，

T_n(\theta) = \cos (n\theta)

のように表される関数で，基底関数としてよい性質を持っています．一次から五次までのChebyshev多項式を図示すると，

のようになります．Chebyshev多項式についてまとめられている資料をいくつか挙げておきます．

• 京都大学 竹広先生のノート： チェビシェフ関数変換法
• 九州大学 吉田先生のノート： 直交多項式
• @cometscome_phys さんの記事： チェビシェフ多項式による関数近似:Juliaで眺めてみる。

さて， $i$ 番要素での物理量 $u^i(\bar{x})$ をChebyshev多項式 $T_n$ を使って表します．$i$ 番要素の $j$ 次展開係数を $u_j^i$ と書くことにして，

\begin{align}
u^i(\bar{x}) &= \sum_{j=0}^{N_x^i} u_j^i h_j^i(\bar{x}^i) \\
h_j^i(\bar{x}^i) &= \frac{2}{N_i^x} \sum_{j=0}^{N_x^i} \frac{1}{\bar{c}_j \bar{c}_n} T_n(\bar{x}_j^i) T_n(\bar{x}^i)
\end{align}

[](

  a_{n}^i = \sum_{n=0}^{N_{x}^i} \beta_{n,j} u(x_q) T_{n}(\bar{x}_{j}^i)

)

\begin{align}
\bar{c}_k =\left\{ \begin{array}{ll}
  1 & (k\neq0, N_{x}^i) \\
  2 & (k=0, N_{x}^i) \\
\end{array} \right.
\end{align}

[](

\begin{align}
\beta_{n,j} =\left\{ \begin{array}{ll}
  1/4 & (n=0,~j=0 ~\mathrm{or}~ N_{x}^i) \\
  1/2 & (n=0,~j: ~\mathrm{else}) \\
  1/2 & (n \ne 0,~j=0 ~\mathrm{or}~ N_{x}^i) \\
  1   & (n \ne 0,~j: ~\mathrm{else}) \\
\end{array} \right.
\end{align}

)

となります．$h_j^i$ は $i$ 番要素以外でゼロであり，Lagrange補間の性質

h_j^i(\bar{x}_k^i) = \delta_{jk}

を満たしています．このことから， 展開関数であるChebyshev多項式の次数=要素内の離散点数 であることが分かります．

次節以降で，Helmholtz方程式（の弱形式による定式化）をこの多項式によって展開し，解くべき一次方程式を定めます．
[](
$\bar{c}_k$ として要素境界（を担当するChebyshev多項式の最低次と最高次）における補正が入っていることに注意してください．
)

Helmholtz方程式の定式化

弱形式による定式化

Helmholtz方程式をスペクトル要素法で近似する（つまり，有限要素法と同じく弱形式で定式化し弱解を求める）ことは，次の言明と同値です．

\delta I = 0, ~~ I = \int_{x_{\text{I}}}^{x_{\text{O}}} \Bigl[ -\frac{1}{2} \Big( \frac{\mathrm{d} u}{\mathrm{d} x} \Big)^2 - \frac{\lambda^2}{2} u^2 -uf \Bigr] ~\mathrm{d}x

を満たす$u(x)$を見つける．

[](
まず，この言明と方程式が同値であることを示す．
汎関数$U$を次のように定義する．

U \Big( u, \frac{\partial u}{\partial x} \Big) = -\frac{1}{2} \Big( \frac{\partial u}{\partial x} \Big)^2 - \frac{\lambda^2}{2} u^2 -uf

これによって作用$I$を定義する．

  I = \int_{x_{\text{I}}}^{x_{\text{O}}} U \Big( u, \frac{\partial u}{\partial x} \Big) ~\mathrm{d}x

作用$I$の変分$\delta I$を計算する．

\begin{align}
  \delta I &= \int_{x_{\text{I}}}^{x_{\text{O}}} \Bigl[ U +\delta U \Bigr] ~\mathrm{d}x - \int_{x_{\text{I}}}^{x_{\text{O}}} U ~\mathrm{d}x \\
  &= \int_{x_{\text{I}}}^{x_{\text{O}}} \delta U ~\mathrm{d}x \\
  &= \int_{x_{\text{I}}}^{x_{\text{O}}} \Bigl[ \frac{\partial U}{\partial u} \delta u + \frac{\partial U}{\partial \Big( \frac{\partial u}{\partial x} \Big)} \delta \Big( \frac{\partial u}{\partial x} \Big) \Bigr] ~\mathrm{d}x \\
  &= \int_{x_{\text{I}}}^{x_{\text{O}}} \Bigl[ \frac{\partial U}{\partial u} - \frac{\partial u}{\partial x} \frac{\partial U}{\partial \Big( \frac{\partial u}{\partial x} \Big)} \Bigr] \delta u ~\mathrm{d}x
\end{align}

ただし以下の部分積分の関係を用いる．

\begin{align}
  \int_{x_{\text{I}}}^{x_{\text{O}}} \frac{\partial U}{\partial \Big( \frac{\partial u}{\partial x} \Big)} \delta \Big( \frac{\partial u}{\partial x} \Big) ~\mathrm{d}x
  &= \int_{x_{\text{I}}}^{x_{\text{O}}} \frac{\partial U}{\partial \Big( \frac{\partial u}{\partial x} \Big)} \frac{\partial (\delta u)}{\partial x} ~\mathrm{d}x \\
  &= \Bigl[ \frac{\partial U}{\partial \Big( \frac{\partial u}{\partial x} \Big)} \delta u \Bigr]_{-1}^{1} -\int_{x_{\text{I}}}^{x_{\text{O}}} \frac{\partial}{\partial x} \Bigl[ \frac{\partial U}{\partial \Big( \frac{\partial u}{\partial x} \Big) } \Bigr] \delta u ~\mathrm{d}x \\
  &= 0 -\int_{x_{\text{I}}}^{x_{\text{O}}} \frac{\partial}{\partial x} \Bigl[ \frac{\partial U}{\partial \Big( \frac{\partial u}{\partial x} \Big) } \Bigr] \delta u ~\mathrm{d}x
\end{align}

ここで，$\delta u(x_{\text{I}}) = \delta u(x_{\text{O}}) = 0$なる関係は変分の両端が停留するという要請より導かれた．
以上より作用の変分$\delta I$についてまとめると，Helmholtz方程式が現れる．

\begin{align}
  \delta I &= \int_{x_{\text{I}}}^{x_{\text{O}}} \Bigl[ \frac{\partial U}{\partial u} - \frac{\partial}{\partial x} \frac{\partial U}{\partial \Big( \frac{\partial u}{\partial x} \Big)} \Bigr] \delta u ~\mathrm{d}x \\
  &= \int_{x_{\text{I}}}^{x_{\text{O}}} \frac{\partial U}{\partial u} \delta u ~\mathrm{d} x - \int_{x_{\text{I}}}^{x_{\text{O}}} \frac{\partial}{\partial x} \frac{\partial U}{\partial \Big( \frac{\mathrm{d} u}{\mathrm{d} x} \Big)} \delta u ~\mathrm{d} x \\
  &= \int_{x_{\text{I}}}^{x_{\text{O}}} \Bigl[ -\lambda^2 u -f \Bigr] - \int_{x_{\text{I}}}^{x_{\text{O}}}  \frac{\partial}{\partial x} \Bigl[ -\frac{\partial u}{\partial x} \Bigr] \delta u ~\mathrm{d} x \\
  &= \int_{x_{\text{I}}}^{x_{\text{O}}} \Bigl[ \frac{\partial^2 u}{\partial x^2} -\lambda^2 u -f \Bigr] \delta u ~\mathrm{d} x
\end{align}

よって，Helmholtz方程式の解が見つかるとき，作用の変分が0となる．
以上よりHelmholtz方程式をスペクトル要素近似することが許された．
詳しい説明は省略しますが，上記の積分方程式と与えられた境界条件から，一次元Helmholtz方程式を数値的に解くことができます．
)

これを正当化する議論については，再掲ですが @t_kemmochi さんによる記事や書籍等を参照してください．

要素方程式

Helmholtz方程式の弱形式に対する要素方程式(The elemental equations)を次式で定めます．

\begin{align}
\int_{-1}^1 \Bigl[ -\frac{1}{2} \Big( \frac{\mathrm{d} u}{\mathrm{d} x} \Big)^2 - \frac{\lambda^2}{2} u^2 \Bigr] ~\mathrm{d}x &= \int_{-1}^1 uf  ~\mathrm{d}x \\
( A_{jk}^i -\lambda^2 B_{jk}^i ) u_{k}^i &= B_{jk}^i f_{k}^i
\end{align}

下付き添字のみ総和規約を用いることに注意します．

要素行列は以下より定まります．

\begin{align}
  A_{jk}^i &= \frac{-2}{L^i (N_{x}^i)^2} \frac{4}{\bar{c}_{j}\bar{c}_{k}}
  \sum_{n=0}^{N_{x}^i} \sum_{m=0}^{N_{x}^i} \frac{1}{\bar{c}_{n}\bar{c}_{m}} T_{n}(\bar{x}_j^i) T_{m}(\bar{x}_k^i) a_{nm}; \\
 a_{nm} &= \int_{-1}^{1} \Bigl\{ \frac{\mathrm{d} T_{n}}{\mathrm{d} x} \frac{\mathrm{d} T_{m}}{\mathrm{d} x} \Bigr\} ~\mathrm{d}x, \\
 B_{jk}^i &= \frac{L^i}{2 (N_{x}^i)^2} \frac{4}{\bar{c}_{j}\bar{c}_{k}} \sum_{n=0}^{N_{x}^i} \sum_{m=0}^{N_{x}^i} \frac{1}{\bar{c}_{n}\bar{c}_{m}} T_{n}(\bar{x}_j^i) T_{m}(\bar{x}_k^i) b_{nm}; \\
 b_{nm} &= \int_{-1}^{1} \{ T_n T_m \} ~\mathrm{d}x \nonumber
\end{align}

ここでChebyshev多項式の性質から，

\begin{align}
  a_{nm} &= \int_{-1}^{1} \Bigl\{ \frac{\mathrm{d} T_{n}}{\mathrm{d} x} \frac{\mathrm{d} T_{m}}{\mathrm{d} x} \Bigr\} ~\mathrm{d}x \\
  &= 0, &~~n+m ~~\mathrm{odd} \\
  &= \frac{nm}{2} [J_{|(n-m/2)}-J_{|(n+m/2)}], &~~n+m ~~\mathrm{even} \\
  J_{k} &= -4 \sum_{p=1}^k \frac{1}{2p-1}, &k \ge 1, \\
    &= 0, &k = 0, \\
 b_{nm} &= \int_{-1}^{1} \{ T_n T_m \} ~\mathrm{d}x \nonumber \\
  &= 0, &~~n+m ~~\mathrm{odd}\\
  &= \frac{1}{1-(n+m)^2} +\frac{1}{1-(n-m)^2}, &~~n+m ~~\mathrm{even}
\end{align}

です．これらの性質については先ほど挙げた竹広先生のノートや吉田先生のノートを参照してください．
一見とても複雑な式の羅列ですが，前に述べたChebyshev多項式による物理量の近似式と見比べると，弱形式をChebyshev展開で定義したものであることが分かると思います．

[](
とても複雑に見えますが，本質的には

• $A_{jk}^i$ と $B_{jk}^i$ はChebyshev逆変換
• $a_{nm}$ と $b_{nm}$ はChebyshev多項式 $T_n$ と $T_m$ に対する（導関数の）積を積分したもの
  であり，作用の変分と同じであることが分かります．
  )

大域方程式

各要素で定義された要素方程式を直接剛性法(Direct stiffness method)によって足し上げると，系全体の方程式，

  C_{pq} u_{q} = B_{pq} f_{q}

を得ることができます．直接剛性法における要素行列の足し上げを $B_{jk}^i$ から $B_{pq}$ への演算を例に見てみます．この操作の模式図を示すと，


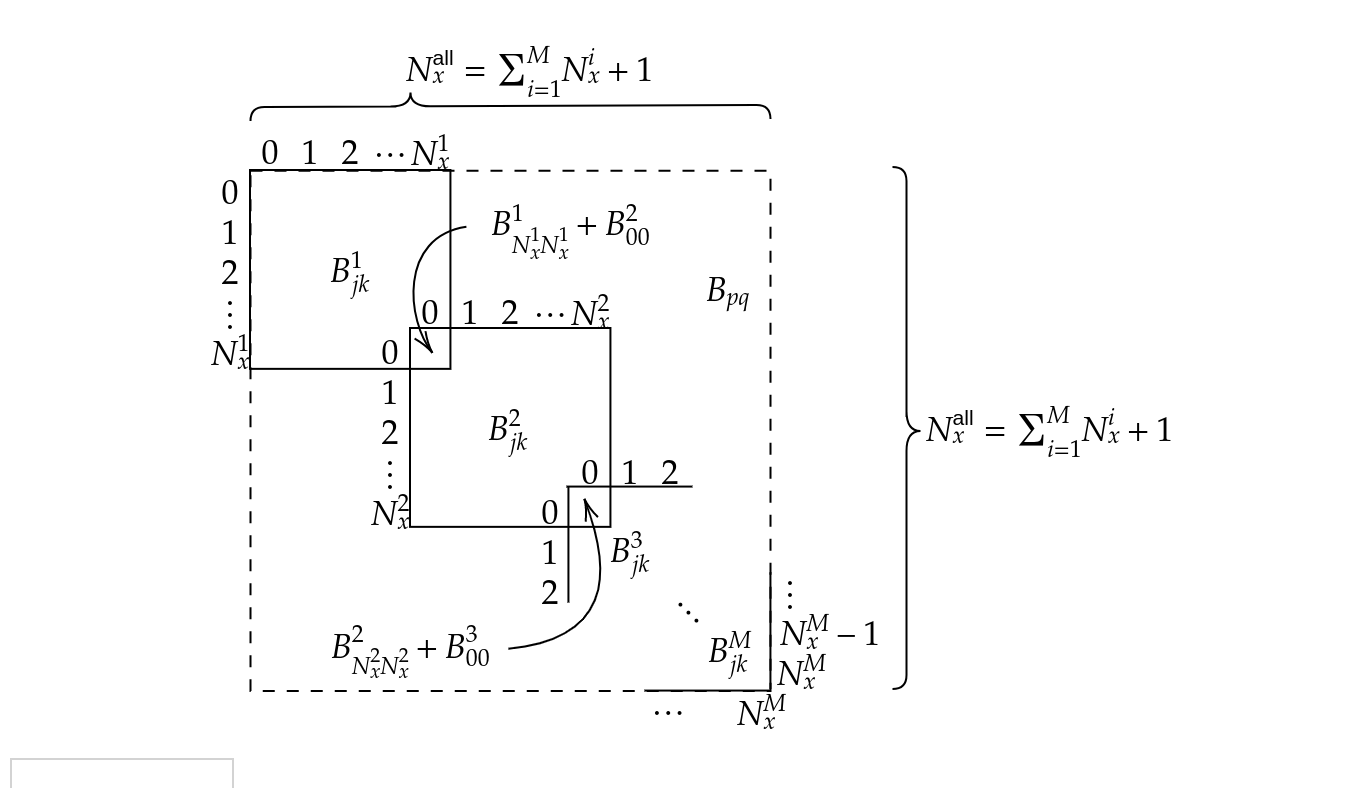
のようになります．図から分かるように，同じ大域座標に対応する要素境界を意味する$B_{N_{x}^i k}^i$行と$B_{0 k}^{i+1}$行，$B_{j N_{x}^i}^i$列と$B_{k 0}^{i+1}$列が重ね合わされています．この処理は有限要素法においても全く一緒ですが，要素内部に相当する行列要素が（重ね合わされず）そのまま残っている点が異なります．
結局，$(N_{x}^i +1) \times (N_{x}^i +1)$の大きさの要素行列 $B_{jk}^i$ を $M$ 要素分足しあげたとき，大域行列 $B_{pq}$ の大きさは $\big(\sum_{i=1}^{M}N_{x}^i +1) \times (\sum_{i=1}^{M}N_{x}^i +1\big)$ となります．この行列の大きさが大域離散点数と一致していることが分かると思います．

境界条件

今回の実装において，Dirichlet境界条件は大域係数行列の対応する行を0とする行列圧縮(Matrix condensation)によって実現できます．この様子を模式図で示すと，


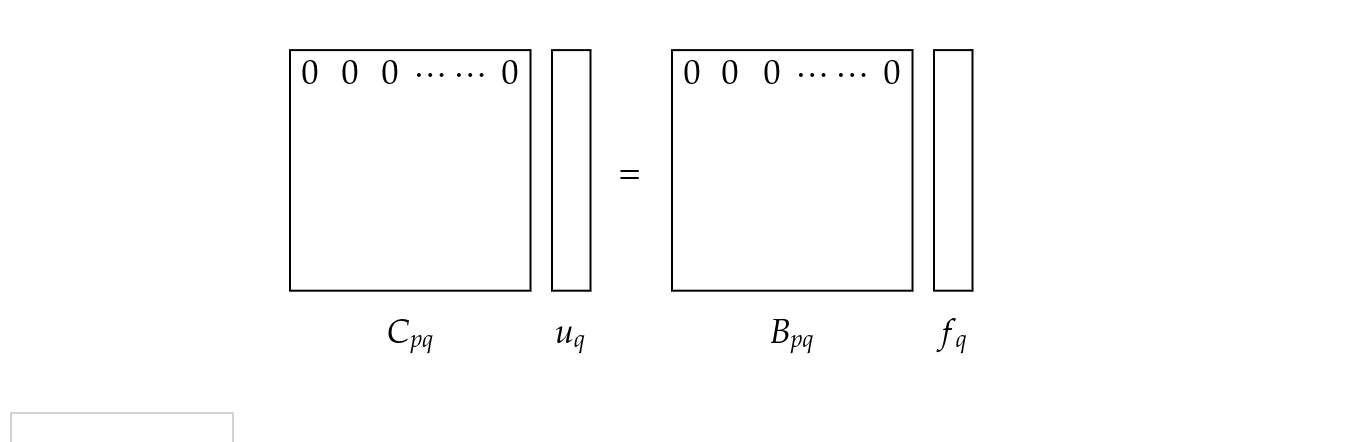
のようになります．

また，ゼロNeumann境界条件は係数行列をそのまま用いることで自然に導入(Naturally imposed)されることが弱形式の定式化から分かります．

実装と計算デモ

今回は，原論文でテスト問題として使われていたのと同じ条件で計算します．⁴

名前	条件
領域	$x \in [-1,1]$
定数項	$\lambda^2 = 0$
外力項	$f = \cos(\pi x+\pi /4)$
上流・下流における境界条件	$u[-1] = 0, u[1]=0$

[](

\begin{align}
\lambda^2 &= 0 \\
f &= \cos(\pi x+\pi /4) \\
x &\in [-1,1] \\
u(-1) &= 0 \\
u(1)  &= 0
\end{align}

)

このときの問題と解析解を示すと，

\begin{align}
\left\{ \begin{array}{l}
  \frac{\mathrm{d}^2 u(x)}{\mathrm{d} x^2} = \cos(\pi x+\pi /4), ~~~~~-1 \le x \le 1 \\
  u(-1) = u(1) = 0 \\
\end{array} \right.
\end{align}

u(x) = \frac{\sin(\pi x) - \cos(\pi x) - 1}{\sqrt{2} \pi^2}

となります．

実装はgithubに置いてあります．
Helmholtz_SEM_Julia
メインの処理は以下の通りです．

## Main
set_initial_condition(param_,var_)
  # 計算に利用する配列の初期化
set_global_x(param_,var_)
  # 大域座標と局所座標の間の変換を定義
set_B_local(param_,var_)
set_C_local(param_,var_)
  # 要素行列を定義
set_B_global(param_,var_)
set_C_global(param_,var_)
  # 大域行列を定義（直接剛性法による足しあげ）
set_f_local(param_,var_)
  # 局所座標での外力項を定義
set_f_global(param_,var_)
  # 大域座標での外力項を定義（直接剛性法による足しあげ）
set_RHS(param_,var_)
  # 大域右辺ベクトルを定義
var_.u = solve_LineraEquation(param_,var_)
  # 線形方程式を反復解法で解き，解を求める

結果

様々な要素数 $M$ と要素内離散点数 $N_x^i$ に対する数値解を，解析解と共に示します．

• 要素数 $M=2$ ，要素内離散点数（=Chebyshev多項式の次数） $N_x^i=3$
  

• 要素数 $M=4$ ，要素内離散点数 $N_x^i=6$
  

• 要素数 $M=8$ ，要素内離散点数 $N_x^i=10$
  

計算点数（ $\leftrightarrow$ 要素数，要素内離散点数）を増加させると，数値解が解析解とよく一致していくことがわかります．

要素数/離散点数による収束

解に対する要素数および要素内離散点数の影響をみていきます．

• 要素数 $M=2,3,4$ ，要素内離散点数 $N_x^i=6$ に固定
  

• 要素数 $M=2$ に固定，要素内離散点数 $N_x^i=3,5,7,9$
  

離散点の増加に伴い，それ以外の補間誤差（interpolant error）が減少していっていることが分かります．また，原論文では要素数を固定したとき要素内離散点数（=Chebyshev多項式の次数）に対して $L^\infty$ 誤差が指数的に減少することが述べられています．⁵

スペクトル要素法：応用

ここまで，スペクトル要素法が初めて提唱された論文に基づいて実装をおこなってきました．そのため，現在実際に使われている手法は今回実装したものとはかなり異なります．⁶
最近のスペクトル要素法について勉強したいという方は，例えば，
Spectral/hp Element Methods for Computational Fluid Dynamics
を参照してください．さらに最新の情報としては，この書籍の著者の一人でもあるS. Sherwin教授らのグループによるレビュー論文，
Spectral/hp element methods: recent developments, applications, and perspectives（Arxiv）
があります．

また，流体解析ソルバとしてスペクトル要素法を用いているものに，

• Nektar++
  • University of UtahのM. Kirby教授，Imperial College LondonのS. Sherwin教授らの主導するプロジェクト
• semtex
  • Monash UniversityのH. Blackburn教授によるプロジェクト．
  • 3次元Cartesian座標系に加え，Fourier展開を用いた一次元周期性のある系にも対応している
• NEK5000
  • University of IllinoisのP. Fischer教授の主導するプロジェクト
  • 導入された方の記事： Nek5000をインストールしてみた

などがあります．ぜひ試してみて（そしてインストール方法や使い方をQiitaにまとめてみて）ください！

参考文献

Anthony Patera, A spectral element method for fluid dynamics: Laminar flow in a channel expansion
G. Karniadakis and S. Sherwin, Spectral/hp Element Methods for Computational Fluid Dynamics
竹広真一，チェビシェフ関数変換法
吉田茂生，直交多項式
チェビシェフ多項式による関数近似:Juliaで眺めてみる。
Juliaで数値計算　その1：コードサンプル〜基本的計算編〜
Julia言語と Plots + GR で複素関数のgifアニメーションを作る

1. 要素数を増やした場合の誤差が代数的に減少する，という方が適切かもしれません． ↩

2. これはごく大雑把な「お気持ち」程度の定義です．厳密な定義は書籍・論文等にあたってください．また，私が誤解している点がありましたらご指摘ください． ↩

3. なお，執筆者の力不足から関数解析を用いたスペクトル要素法の基礎づけについては満足な議論ができておりません．申し訳ありません． ↩

4. $\lambda^2=0$ としているためPoisson方程式になっており記事タイトルから外れていますが，実装はHelmholtz方程式としておこなっています ↩

5. ここまでこの記事で示したかったのですが，原論文に基づいて $L^\infty$ を計算してみても論文通りの図が得られませんでした．バグ，あるいは私自身の理解が間違っている可能性があるため，この部分は宿題としたいと思います（いつかきちんと完成させたいです）． ↩

6. 例えば，展開関数としてはChebyshev多項式ではなくJacobi多項式やLegendre多項式（それらをさらに拡張したもの）などが使われますし，ある方向に周期性をもつ系に対してはFourier展開と2次元スペクトル要素法を組み合わせて解く，といったこともおこなわれています． ↩