この記事では、線形回帰の基本からスタートし、Pythonを使ってLASSOやリッジ回帰などの正則化手法、さらに多項式回帰を用いた非線形回帰まで、幅広く丁寧に解説します。
初心者でも理解しやすいように理論と実装をバランスよく紹介し、データ分析に役立つ回帰モデルの全体像をつかめる内容です。これから回帰分析を学びたい方や、より高度な回帰手法を実践したい方に最適な入門ガイドとなっています。
本記事では以下の流れで説明する。
1 線形回帰
機械学習の教師あり学習には、クラスの所属関係やカテゴリ変数を予測する分類モデル(Classification Analysis)と、連続値を目的変数とする回帰分析(Regression Analysis)があります。
回帰分析の目標は、1つ以上の特徴量と目的変数(連続値)の関係をモデルで表すことにあります。これらの関係性を、線形(直線)で表すモデルを 線形回帰(Linear Regression)と呼びます。線形回帰には、特徴量を1つでモデルを構成する単線形回帰(Simple Linear Regression)と、複数の特徴量を使う重線形回帰(Multiple Linear Regression)(多重線形回帰)があります。
1.1 単線形回帰
単線形回帰は、1つの特徴量を持つので式で表すと以下のようになります。
$$
y = w_0 + w_1x
$$
回帰分析では、訓練データを通過する直線のうち最も適合するものを見つけ出すことを意味します。この最も適合する直線を回帰直線(Regression Line)と呼び、回帰直線から、訓練データへの縦線を残差(Residual)と呼びます。
1.2 重線形回帰
単線形回帰に対して、複数の特徴量を持つ線形回帰を重回帰分析と呼びます。上式では、$x_0$=1として、$w_0$はy軸の切片を表しています。
$$
y = w_0 x_0 + w_1 x_1 + \cdots + w_m x_m = \sum^m_{i=0}w_ix_i = \mathbf{w}^T\mathbf{x}
$$
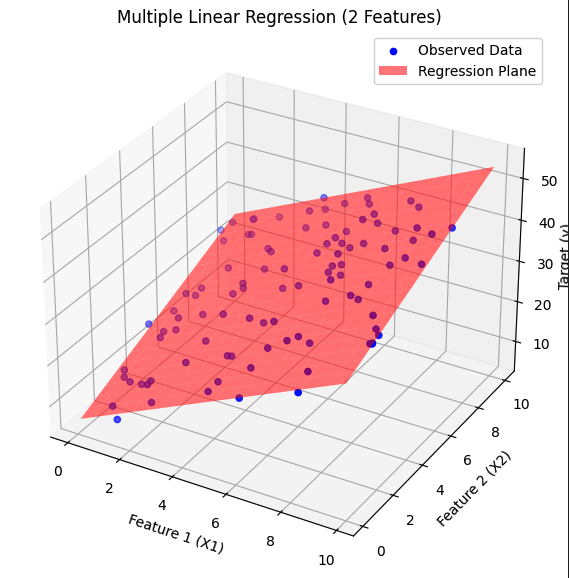
下図は、特徴量が2つの重回帰モデルの超平面が3次元の散布図として図示されたものです。
重回帰の超平面を書くコード
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from mpl_toolkits.mplot3d import Axes3D
# 1. 適当なデータを生成
np.random.seed(0)
n_samples = 100
X1 = np.random.rand(n_samples) * 10 # 特徴量1
X2 = np.random.rand(n_samples) * 10 # 特徴量2
noise = np.random.randn(n_samples) * 2 # ノイズ
# 目的変数(線形モデルにノイズを加える)
y = 3 * X1 + 2 * X2 + 5 + noise
# 特徴量を結合
X = np.column_stack((X1, X2))
# 2. 線形回帰モデルを学習
model = LinearRegression()
model.fit(X, y)
# 3. 回帰平面の描写用メッシュグリッド
X1_grid, X2_grid = np.meshgrid(
np.linspace(X1.min(), X1.max(), 20),
np.linspace(X2.min(), X2.max(), 20)
)
X_grid = np.column_stack((X1_grid.ravel(), X2_grid.ravel()))
y_pred_grid = model.predict(X_grid).reshape(X1_grid.shape)
# 4. 3Dプロット
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
# 実データ点の散布図
ax.scatter(X1, X2, y, color='blue', label='Observed Data')
# 回帰平面
ax.plot_surface(X1_grid, X2_grid, y_pred_grid, alpha=0.5, color='red', label='Regression Plane')
# ラベル付け
ax.set_xlabel("Feature 1 (X1)")
ax.set_ylabel("Feature 2 (X2)")
ax.set_zlabel("Target (y)", labelpad=0)
ax.set_title("Multiple Linear Regression (2 Features)")
plt.legend()
plt.show()
1.3 線形回帰のコスト関数
線形回帰とは、「訓練データを通過する直線のうち最も適合するものを見つけ出すこと」と説明しましたが、この直線はどのように見つけるのでしょうか?線形回帰では、訓練データと回帰直線との縦の距離、すなわち残差の2乗和を最小にする直線を最適な回帰直線とします。この方法を最小二乗法(Ordinary Least Squares: OLS)と呼びます。
線形回帰のコスト関数は、最小二乗法で計算され、以下のように書けます。
$$
\min_{\boldsymbol{w}} \mathbf{J}(\mathbf{w}) = \sum_{i=1}^{n} \left( y_i - \hat{y} \right)^2
$$
ここで、$\hat{y}$は、$\mathbf{w}^\top \mathbf{x}_i$で計算されます。
このコスト関数$\mathbf{J}(w)$を勾配効果法などを使って、最小化することで、最適なパラメータ$w_i$を見つけます。
1.4 線形回帰の評価指標
線形回帰モデルの評価指標としてとよく使われるのが、平均二乗誤差(Mean Squared Error:MSE)と決定係数($R^2$)です。MSEは、予測値と実際の値の差(残差)の 二乗の平均 を取ったもので、「予測がどれだけ実際とズレているか」の平均的な大きさを表します。
$$
$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
$$
MSEは値が小さいほど、予測精度が高いことを示しています。MSEは直感的に理解しやすい手法ですが、その反面単位が目的変数の二乗の単位なので、目的変数のスケールに依存し、残差を二乗しているため外れ値の影響を受けやすいという特徴があります。
次に、決定係数はモデルがどれだけデータの変動を説明できるかを表す指標として、0~1の範囲で計算され、1に近いほど良いモデルとされます。
R^2=1-\frac{\sum_{i=1}^n(y_i - \hat{y_i})^2}{\sum_{i=1}^n(y_i - \bar{y})^2}
上式で、分母は全変動(Total Sum of Squares, TSS)、分子は残差平方和(Residual Sum of Squares, RSS)と呼ばれます。分母の全変動は、常に平均 $\bar{y}$ で予測するという超単純なモデル(ベースライン)による誤差を表しています。それに対して、分子の残差平方和は自分のモデルが予測した値 $\hat{y}_i$ と実際の値 $y_i$ のズレの合計(二乗)です。そのため、決定係数が計算している比率とはベースラインと比べて、モデルがどれだけ誤差を減らしたかを示します。
決定係数は単位を持たないため、他のモデルとの比較を行いやすいといったメリットがあります。
1.5 線形回帰の実装
ここでは、Housingデータセットを使用して実装を行っていきます。データセットは、こちらからダウンロードできます。詳しいデータセットの説明などは、こちらを参考にしてください。
Housingデータセットをインポート
import pandas as pd
url = "https://raw.githubusercontent.com/rasbt/python-machine-learning-book-3rd-edition/master/ch10/housing.data.txt"
# データの読み込み
df = pd.read_csv(url, delim_whitespace=True, header=None)
df.columns = [
"CRIM", "ZN", "INDUS", "CHAS", "NOX", "RM", "AGE", "DIS", "RAD", "TAX", "PTRATIO", "B", "LSTAT", "MEDV"
]
X = df[["RM", "LSTAT"]].values # 特徴量として「部屋数」と「低所得者の割合」を使用
y = df["MEDV"].values # 目的変数として「住宅価格」を使用
print(df.head())
特徴量を2つだけ使って、重回帰分析を行います。scikit-learnのLinearRegressionモジュールを使うと簡単に実装できます。
# 回帰分析を実装する
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
# データの標準化
scaler = StandardScaler()
X = scaler.fit_transform(X)
y = scaler.fit_transform(y.reshape(-1, 1)).flatten()
# 線形回帰モデルのインスタンスを作成
model = LinearRegression()
# モデルを学習
model.fit(X, y)
# 予測値を計算
y_pred = model.predict(X)
# 平均二乗誤差を計算
mse = mean_squared_error(y, y_pred)
print(f"平均二乗誤差 (MSE): {mse:.2f}")
# 平均二乗誤差 (MSE): 0.36
# 回帰係数と切片、決定係数を表示
r2 = r2_score(y, y_pred)
print(f"回帰係数: {model.coef_[0]:.2f}, {model.coef_[1]:.2f}")
print(f"切片: {model.intercept_:.2f}")
print(f"決定係数 (R^2): {r2:.2f}")
# 回帰係数: 0.39, -0.50
# 切片: 0.00
# 決定係数 (R^2): 0.64
ここで求められた回帰分析の超平面を図示と以下のようになります。

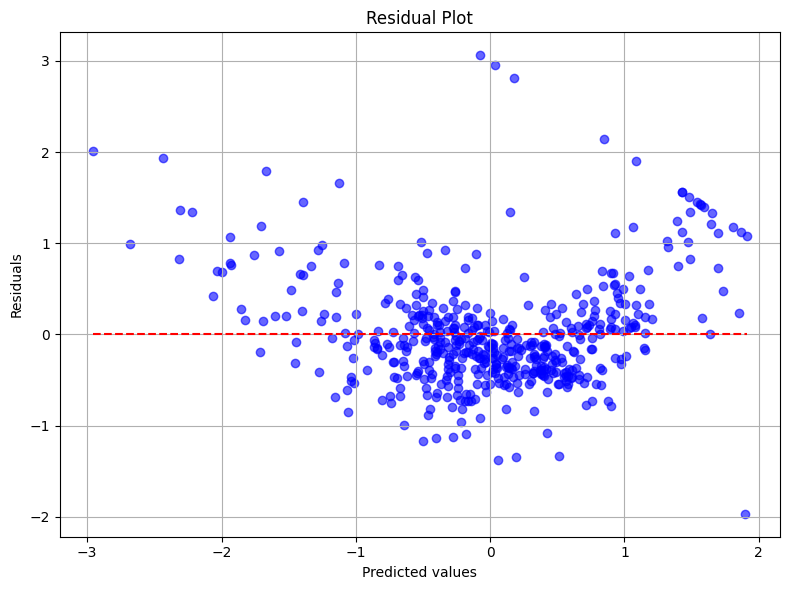
さらなる線形回帰モデルの性能評価として、残差プロット(Residual Plot)を確認するグラフィカルな解析手法を用いることもできます。良い回帰モデルは、残差が0に近いことに加えて、残差がランダムに分布し、中央の回帰直線の周りにランダムに散らばります。もし、残差プロットに何かしらのパターンが見られる場合は、モデルが何かしらの説明情報を捕捉できていないことを示唆しています。
以下は、今回の実装で作成したモデルにおける残差プロットです。これを見ると、残差はランダムに分布しておらず何かしらのパターンが存在しているように見えます。
2 正則化と回帰分析
正則化は、モデルの極端なパラメータの重みにペナルティを科すことで、過学習を抑制する手法です。正則化された線形回帰の最も一般的なアプローチは、リッジ回帰(Ridge Regression)、LASSO(Least Absolute Shrinkage and Selection Operator)、Elastic Net法の3つです。
リッジ回帰は、L2ペナルティ付きの線形回帰です。そのため、最小二乗法コスト関数に対して、L2正則化項を追加します。
\mathbf{J}(\mathbf{w})_{Ridge} = \sum_{i=1}^{n} \left( y_i - \hat{y} \right)^2 + \lambda||w||^2_2
LASSOはL1正則化を用いた手法なので、上式のL2正則化項をL1正則化項($\lambda||w||_1$)に置き換えるだけです。
Elastic Netはこの両者の折衷案で、L1ペナルティは疎性を生成するために使われ、L2ペナルティは$m>n$の場合に特徴量をn個よりも多く選択するために使われます。Elastic Netは、LASSOのように変数選択(疎性)を行いながら、リッジ回帰のように相関のある変数に対して安定した推定を可能にするという利点があります。特に、多重共線性のある場合や、LASSOでは変数選択しきれない場合に有効です。
\mathbf{J}(\mathbf{w})_{Elastic Net} = \sum_{i=1}^{n} \left( y_i - \hat{y} \right)^2 + \lambda_1 \sum^m_{j=1}|w_j|^2 + \lambda_2 \sum^m_{j=1}|w_j|
それぞれの実装は、scikit-learnでサポートされているモジュールを使えば良いです。以下では、それぞれの回帰器の初期化の実装コードを紹介します。
from sklearn.linear_model import Ridge, Lasso, ElasticNet
# リッジ回帰
ridge_model = Ridge(alpha=1.0)
# LASSO回帰
lasso_model = Lasso(alpha=0.1)
# エラスティックネット回帰
elastic_net_model = ElasticNet(alpha=0.1, l1_ratio=0.5)
3 非線形回帰
2次以上の項(多項式の項)を回帰式に含むモデルを多項式回帰モデルと呼び、これを使うことで非線形な回帰分析を行うことができます。
y = w_0 + w_1x_1 + w_2x^2 \cdots + w_dx^d
3.1 非線形回帰の実装
これまでの実装と同様にHousingデータセットに対して、非線形回帰を行なってみます。scikit-learnのPolynomialFeaturesクラスを使います。たとえば、2つの特徴量 $x_1$, $x_2$ を用いた場合、1次の線形回帰の式は以下のように書けます。
1次式
$$
\hat{y} = \beta_0 + \beta_1 x_1 + \beta_2 x_2
$$
そこで、degree=2 では以下のような多項式特徴量が生成され、2次の回帰式ができます:
$$
\hat{y} = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1^2 + \beta_4 x_1 x_2 + \beta_5 x_2^2
$$
degree=3 では以下のような多項式特徴量が生成され、3次の回帰式ができます:
$$
\hat{y} = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1^2 + \beta_4 x_1 x_2 + \beta_5 x_2^2 + \beta_6 x_1^3 + \beta_7 x_1^2 x_2 + \beta_8 x_1 x_2^2 + \beta_9 x_2^3
$$
from sklearn.preprocessing import PolynomialFeatures
lr = LinearRegression()
# 多項式特徴量の生成
quadratic = PolynomialFeatures(degree=2, include_bias=False)
cubic = PolynomialFeatures(degree=3, include_bias=False)
# 特徴量を変換
X_quadratic = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)
# 2次の多項式回帰モデルの学習
lr.fit(X_quadratic, y)
y_pred_quadratic = lr.predict(X_quadratic)
# 3次の多項式回帰モデルの学習
lr.fit(X_cubic, y)
y_pred_cubic = lr.predict(X_cubic)
# それぞれのモデルのMSEと決定係数を計算
from sklearn.metrics import mean_squared_error, r2_score
mse_quadratic = mean_squared_error(y, y_pred_quadratic)
mse_cubic = mean_squared_error(y, y_pred_cubic)
r2_quadratic = r2_score(y, y_pred_quadratic)
r2_cubic = r2_score(y, y_pred_cubic)
print(f"2次の多項式回帰 - MSE: {mse_quadratic:.2f}, R^2: {r2_quadratic:.2f}")
print(f"3次の多項式回帰 - MSE: {mse_cubic:.2f}, R^2: {r2_cubic:.2f}")
# 2次の多項式回帰 - MSE: 0.24, R^2: 0.76
# 3次の多項式回帰 - MSE: 0.23, R^2: 0.77
今回の実装では、1次式<2次式<3次式の順で予測精度が向上したのがわかります。ただし、多項式の次数を上げると表現力が高まる一方で、過学習のリスクも増すため、検証データによる評価や交差検証などを通じて適切な次数を選定する必要があります。

今回の回帰分析で作成された超平面です。左図は2次の多項式回帰、右図は3次の多項式回帰で得られた超平面を示しています。次数が上がるにつれて、よりデータの曲面にフィットする形状になっていることが視覚的にも確認できます。
超平面を出力するコード
from mpl_toolkits.mplot3d import Axes3D
# グリッド生成用の元データを取得
x1 = X[:, 0]
x2 = X[:, 1]
# 描画用グリッド作成
x1_range = np.linspace(x1.min(), x1.max(), 30)
x2_range = np.linspace(x2.min(), x2.max(), 30)
x1_grid, x2_grid = np.meshgrid(x1_range, x2_range)
X_grid = np.c_[x1_grid.ravel(), x2_grid.ravel()]
# 2次元特徴量に変換
X_grid_quad = quadratic.transform(X_grid)
X_grid_cubic = cubic.transform(X_grid)
# 2つの別々のモデルを使う
lr_quad = LinearRegression()
lr_quad.fit(X_quadratic, y)
z_quad = lr_quad.predict(X_grid_quad).reshape(x1_grid.shape)
lr_cub = LinearRegression()
lr_cub.fit(X_cubic, y)
z_cub = lr_cub.predict(X_grid_cubic).reshape(x1_grid.shape)
# 3Dプロット
fig = plt.figure(figsize=(16, 6))
# 2次のプロット
ax1 = fig.add_subplot(1, 2, 1, projection="3d")
ax1.scatter(x1, x2, y, color="blue", label="data", alpha=0.5)
ax1.plot_surface(x1_grid, x2_grid, z_quad, color="orange", alpha=0.6)
ax1.set_title("2nd-degree Polynomial Regression")
ax1.set_xlabel("RM (standardized)")
ax1.set_ylabel("LSTAT (standardized)")
ax1.set_zlabel("MEDV (standardized)")
# 3rd-degree Polynomial Regression plot
ax2 = fig.add_subplot(1, 2, 2, projection="3d")
ax2.scatter(x1, x2, y, color="blue", label="data", alpha=0.5)
ax2.plot_surface(x1_grid, x2_grid, z_cub, color="green", alpha=0.6)
ax2.set_title("3rd-degree Polynomial Regression")
ax2.set_xlabel("RM (standardized)")
ax2.set_ylabel("LSTAT (standardized)")
ax2.set_zlabel("MEDV (standardized)")
plt.tight_layout()
plt.show()
4 データの可視化
機械学習モデルの訓練する前に、分析しようとしているデータを理解することはとても重要です。ここでは、探索的データ解析(Exploratory Data Analysis:EDA)の手法のうち、散布図行列とピアソンの積率相関係数について説明します。
以下のコードを実行すると、散布図行列が作成できます。散布図行列を利用すれば、データセットの特徴量のペアに対する相関関係を1つの平面上で可視化できます。ここでは、mlxtendパッケージを利用すると、簡単に実行することができます。
from mlxtend.plotting import scatterplotmatrix
cols = ["RM", "LSTAT", "MEDV", "CRIM", "ZN"]
scatterplotmatrix(df[cols].values, figsize=(10, 10), names=cols, alpha=0.5)
plt.tight_layout()
plt.show()
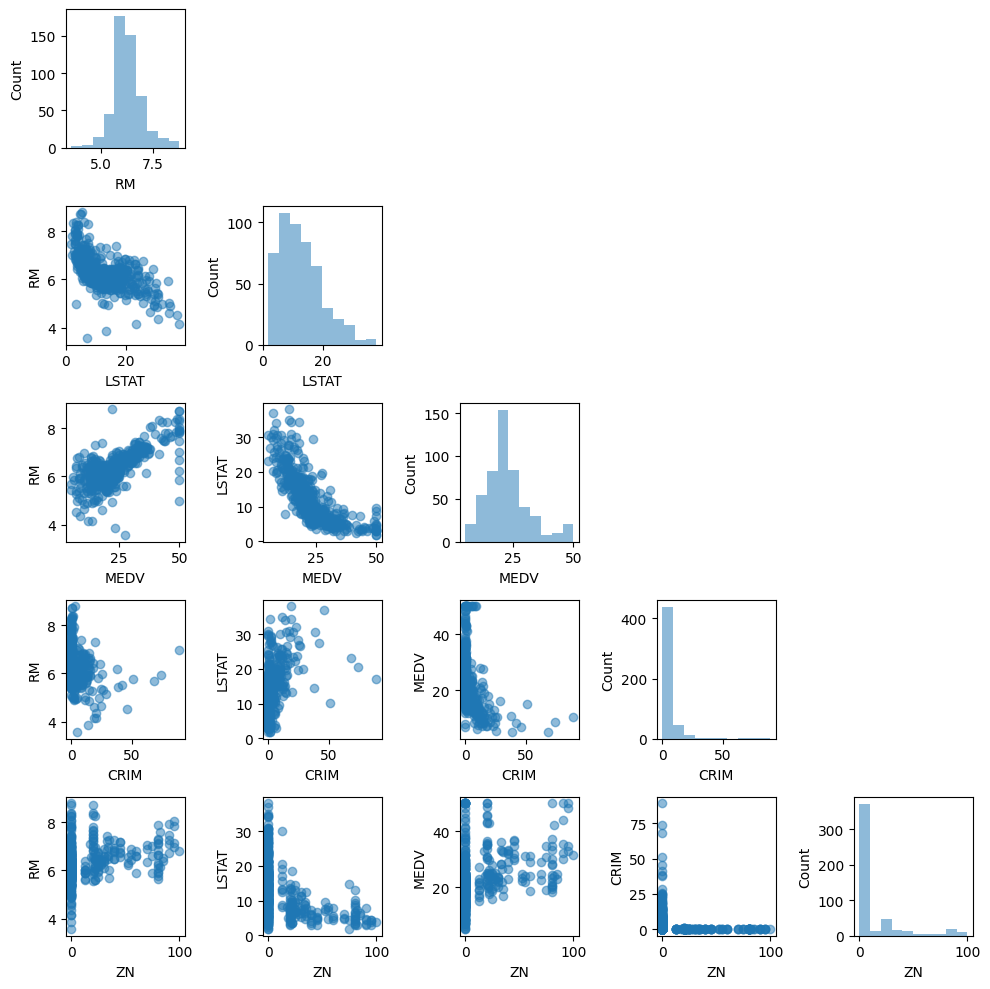
次に、ピアソンの積率相関係数を計算します。これは、特徴量のペアの線形的な従属関係を数値化するもので、-1~1の範囲で表現されます。値が1に近いほど正の相関関係を示し、-1に近いほど負の相関関係を持つことが分かります。ピアソンの積率相関係数は2つの特徴量xとyの共分散をそれらの標準誤差の積で割ったものです。
r = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}
{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}} = \frac{\sigma_{xy}}{\sigma_x \sigma_y}
ピアソンの積率相関係数はmlxtendのheatmap関数を用いて、ヒートマップとして出力することができます。
from mlxtend.plotting import heatmap
cm = np.corrcoef(df[cols].values.T)
heatmap(cm, row_names=cols, column_names=cols, figsize=(8, 6), cmap="coolwarm")
plt.tight_layout()
plt.show()
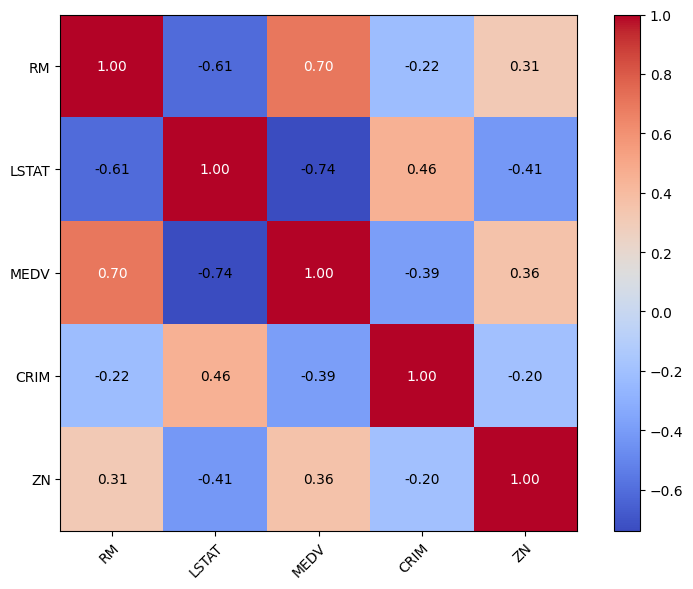
このほかもEDAのコツや、手法は多々あるりますが、いつか別記事にて紹介したいと思います。
5 多重共線性
線形回帰分析、特に複数の特徴量(説明変数)を使う重回帰分析では、モデルの精度や解釈に影響を及ぼす多重共線性(Multicollinearity)という問題に注意が必要です。多重共線性とは、説明変数同士に強い相関関係がある状態を指します。これは、ある説明変数が他の説明変数によって線形的に予測できてしまう場合に起こります。
多重共線性が発生すると、様々な問題が発生します。
- 回帰係数の推定値が不安定になる(わずかなデータの変化で大きく変動する)
- 回帰係数の解釈が困難になる(本当に影響を与えている変数が分かりにくくなる)
- モデルの過学習や汎化性能の低下の原因にもなる
- 回帰係数の符号(正・負)が直感と異なる
- 有意であるはずの変数が統計的に有意でない(p値が高い)
- モデル全体の決定係数$R^2$は高いのに、各変数の有意性が低い
つまり、モデルとしては「よく当てはまっている」ように見えても、中身を信頼できないという状態です。
多重共線性を見つけるためには、特徴量同士の相関係数を確認することや、VIF(Variance Inflation Factor:分散拡大係数)を確認することが有効です。VIFは、ある変数が他の変数によってどれだけ説明されているかを数値化した指標で、値が10以上の場合、多重共線性の可能性が高いとされます。
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant
# 使いたい特徴量をDataFrameから抽出
features = ["RM", "LSTAT", "MEDV", "CRIM", "ZN"]
X_df = df[features]
# 定数項を追加(VIFの計算では必須)
X_const = add_constant(X_df)
# VIFを計算
vif_df = pd.DataFrame()
vif_df["feature"] = X_df.columns
vif_df["VIF"] = [variance_inflation_factor(X_const.values, i + 1) for i in range(X_df.shape[1])]
print(vif_df)
# VIFの結果を表示
# feature VIF
# 0 RM 2.069501
# 1 LSTAT 2.624094
# 2 MEDV 2.833195
# 3 CRIM 1.297794
# 4 ZN 1.218369
多重共線性が見つかった場合の対策には、以下のような方法があります:
- 相関の強い変数のいずれかを削除する
- 主成分分析(PCA)で次元を削減する
- L2正則化(Ridge回帰)を用いて回帰係数の変動を抑制する
出典
Python機械学習プログラミング 達人データサイエンティストによる理論と実践の第10章を参考にしている。
本記事で用いたPythonとライブラリのバージョン
Python version: 3.10.4
pandas version: 2.2.3
scikit-learn version: 1.6.1
matplotlib version: 3.10.1
numpy version: 2.2.5
statsmodels version: 0.14.4
