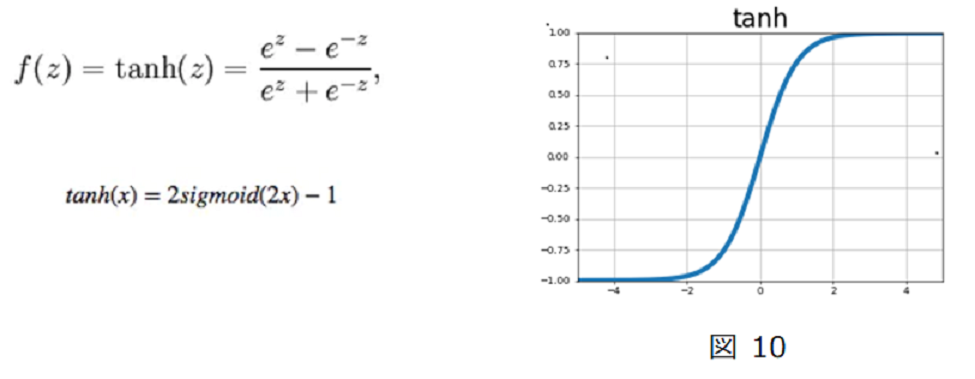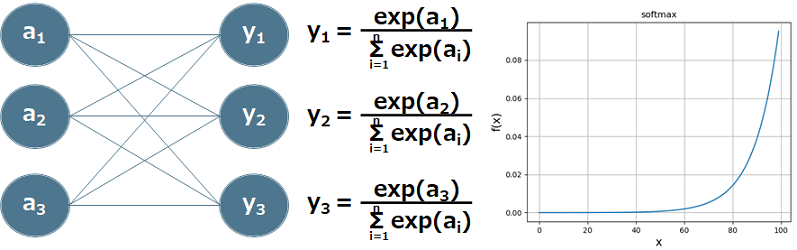本書はディープラーニング手法の各種モデルのベースとなっているCNNについて、説明します。
CNNの説明の前に初心者の方向けにDeep Learningの基本について記載します。(極力従来のアプリケーション開発を実施してきたエンジニアが理解しやすいように記載をしています)
1.背景
現在のAI(人口知能)の発展を支えている基礎技術は機械学習です。
機械学習は、データから正解を導き出すルール(≒Deep Learningにおける重み)を自動的に生成するもので、従来のアプリケーション開発のようにルールを設計しコーディングするプロセスとは全く異なったアプローチをします。その中でもDeep Learningは、特徴量の判断や調整を自動的に設定、学習するという特徴があります。そのため、Deep Learningは、人の認識・判断では限界があった分野(画像認識・翻訳・自動運転の分野等)での活用が特に期待されています。

$$ 図\hspace{1mm}1 従来プログラムと機械学習の比較 $$
また、教師あり学習、教師なし学習、強化学習といった学習手法や、識別モデルや生成モデルといったモデルなど、現在でも発展が目覚ましい分野です。
2.Deep Learningの基礎
Deep Learningは、従来の開発でルールを階層化して実装するように、何層にも処理を重ねた形をしています。学習は各処理で持っているパラメータ(ルール=重み)を最適化する処理です。(一般には層が多いほど精度が高くなります。これは、層が多いほど複雑な特徴を表現できるためですが、その一方で学習が複雑になるという問題があります。)
Deep Learningに使われる演算の代表的なものとしては、データからモデルを形成する処理(Feedforward)と、パラメータを最適化(更新)するために誤差をフィードバックする処理(Backpropagation)があります。
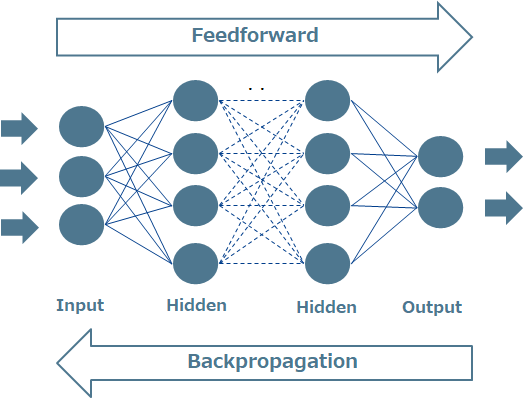
$ \hspace{20mm} 図\hspace{1mm}2 Deep Learning \hspace{2mm} 概要 $
CNNは、データを上下左右の関係をもった二次元で扱うため、画像認識に使われることが多いネットワークです。現在では画像認識だけでなくテキストや音声、感情分析など幅広い領域に応用されるようになってきています。各種モデルのベースとなっているCNNを通してDeep Learningの基本を学習してください。
3.CNNの概要
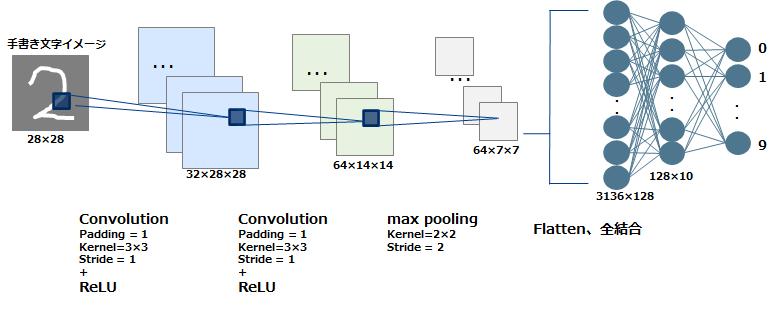
$$ 図\hspace{1mm}3 CNNネットワーク概略図 $$
- ※Convolutionは4.1、ReLUは4.2、Max poolingは4.3、全結合は4.4章を参照してください
- CNNは主に特徴を抽出する「Convolutionレイヤ(畳み込み層)」と畳み込んだデータ(特徴マップ)の解像度を下げる「Poolingレイヤ(プーリング層)」を階層化した構造をしています。 畳み込み層とプーリング層では入力のニューロンの一部の領域を絞って、局所的に次の層へと対応付けをしていきます。また、各層はフィルタ(カーネルともいう)と呼ばれる検出器を複数持っています。 最初の層ではエッジなど低レベルな情報を検出し、層が深くなるにしたがってより抽象的な特徴を検出していきます。CNNはこういった特徴を抽出するための検出器であるフィルタのパラメータを自動で学習していきます。 最終的には出力に近い層では、全結合により分類などを行います(上記の例では、数字0~9の10分類のスコア・確率を出力します)。
- [参考]上記のような多クラス分類においてOne-Hot ベクトルがよく用いられます。One-Hotベクトルとは、「1」が1つ、他はすべて「0」が並ぶベクトルです。分類したいカテゴリの数と同じ次元のベクトルを用意し、対応するカテゴリに1を割り当てて表現するものです。画像分類のほかにも自然言語の単語表現など各カテゴリが独立になっている場合に用いられる表現手法です。
4.CNNの構成
(1) 畳み込み層(Convolutionレイヤ)
脳の単純型細胞をモデル化したもので、元の画像からフィルタにより特徴点を凝縮する(画像から局所的な特徴を抽出)処理です。
ⅰ) 畳み込み演算
畳み込み演算は、下図に示すように入力データに対してフィルタ(カーネルともいう)を適用します。入力データに対してフィルタのウィンドウを一定の間隔(ストライド)でスライドさせながら演算を行います。具体的には入力データの左上からフィルタを順次重ねてフィルタの要素と入力データの対応する要素を乗算しそれの和を求めて(積和演算という)、出力結果の対応する場所(左上から順)に格納します。
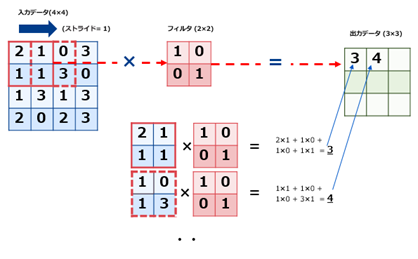
$ \hspace{20mm} 図\hspace{1mm}4 畳み込み演算のイメージ $
ⅱ) ゼロパディングとストライド
畳み込みを行うとそのままでは出力サイズは縮小されます(ex.上記の図では4×4 -> 3×3)。これでは畳み込みを繰り返していくとある時点で出力サイズが1になってしまいそれ以上は畳み込みが出来なくなってしまいます。これを回避するために入力データの周囲を固定のデータ(ゼロ)で埋め込むゼロパティングを行います。畳み込み演算を実施しても元のサイズを保つたり、縮小するサイズを軽減することが可能になります。
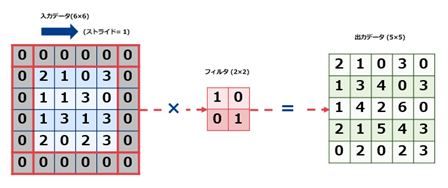
$ \hspace{20mm} 図\hspace{1mm}5 ゼロパディングの例 $
なお、通常ディープラーニングのAIフレームワーク(後述)では、畳み込み演算の関数パラメータで「Same」というパラメータが用意されており、「Same」を設定すると畳み込み演算前後でのサイズは同一となるようにゼロパディングのサイズを自動調整してくれます。
一方、フィルタの間隔をストライド(stride)と言います。
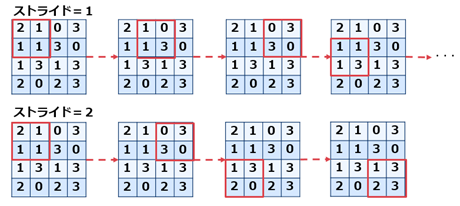
$ \hspace{30mm} 図\hspace{1mm}6 ストライドの例 $
パディングやストライドの値を考慮した出力サイズは以下の計算式で求めることが可能です。
出力サイズ = {(入力サイズ + 2×パディングサイズ - フィルタサイズ)/ ストライドサイズ } + 1
(2) 活性化関数
入力信号(データ)の総和を出力信号(データ)に変換するために使用する関数です。y1を処理する関数を活性化関数h(y1)と呼びます。出力は y=h(y1)で計算されます。
活性化関数は、全結合層や畳み込み層の計算結果を入力として、次の層へどのようにデータを伝播させるかを調整する働きを担っています。
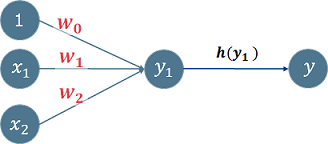
$ \hspace{20mm} 図\hspace{1mm}7 \hspace{2mm} 活性化関数 $
代表的な関数としては以下があります。
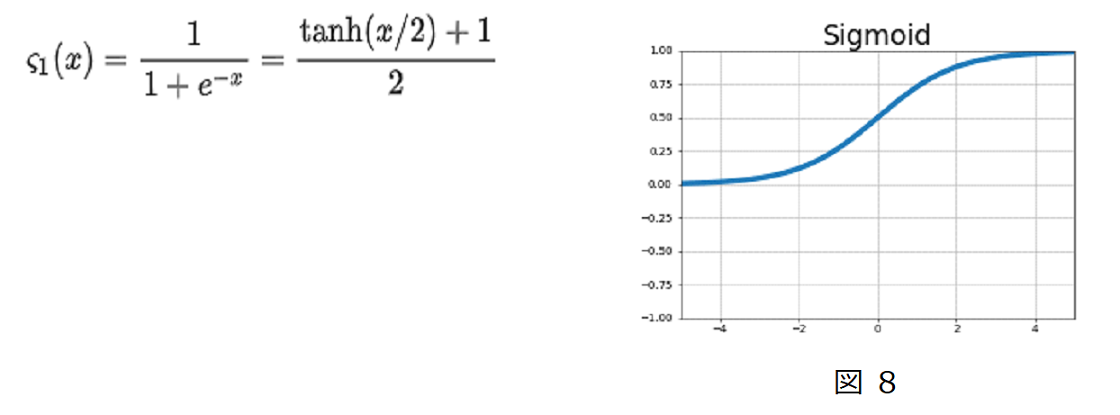
ⅰ) Sigmoid(シグモイド)
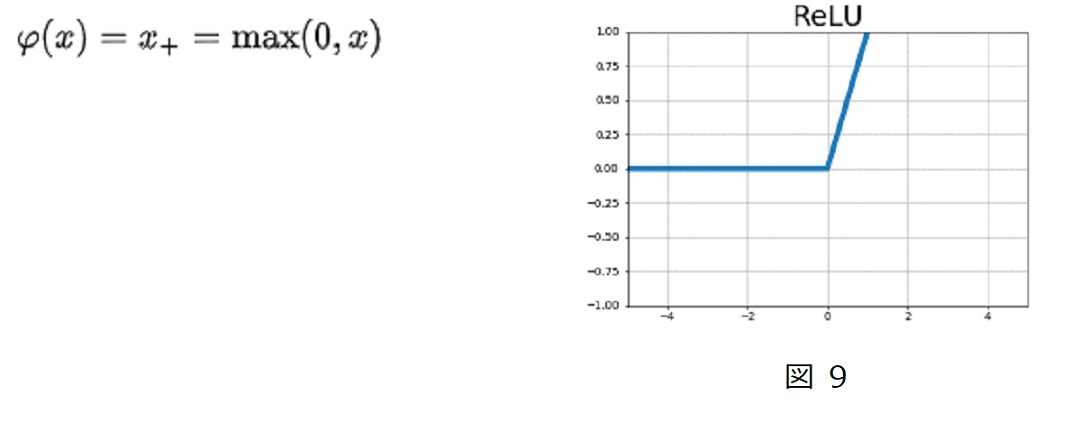
ⅱ) ReLU
出力値を入力が0以下ならば0、0を超えていればその値をそのまま出力します。Sigmoidは出力値が大きくなっても最大1までしか出力しないので学習が遅いという弱点を持っていますが、
ReLUは入力の値が大きくなるに従って出力も大きくなるので、学習が速いというメリットがあります。
ⅲ) tanh
出力値を-1~1の間にします。Sigmoid関数の微分が最大0.25と小さく勾配が小さくなるため学習に時間がかかる、tanhでは、
微分の最大値が1.0となり学習時間の短縮になります。
これらの関数を比べると以下のようになります。
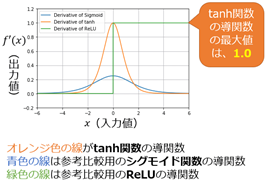
$$ 図 \hspace{1mm}11 \hspace{100mm} $$
ⅳ) ソフトマックス関数(softmax)
ニューラルネットワークは、「分類問題」と「回帰問題」とに分類されますが、どちらに分類するかにより最終出力層の活性化関数が決まります。一般的に、「分類問題」ではソフトマックス関数を、「回帰問題」では恒等関数を用います。
① 恒等関数
恒等関数は入力されたものに対してそのまま出力する関数です。
② ソフトマックス関数
個々の出力が0~1.0に、出力の総和が1.0になる関数です。この性質によりソフトマックス関数の出力を「確率」として使うことができます。
$$ y = exp(a_{k}) / {\sum exp(a_{i})} $$
ⅴ) その他活性化関数
最近のディープラーニングではsigmoidやtanhでは勾配消失問題(特に時系列を扱うRNN系のモデル)が解決できないため、「ReLU」がよく使われています。これは、ReLUであれば入力がゼロ以上であれば勾配(微分)が常に1.0となり勾配消失が起こらないためです。
また、ReLU関数の「負の入力に対しては学習が進まない」という欠点を補うため負の入力の時はごく小さな傾きの1次関数を出力するようにした「Leaky ReLU」や、ReLU関数をX=0のときにより滑らかにした「ELU」、さらにはReLUの後継として微分値がX=0でも連続となる「Swish」や「Mish」等様々な活性化関数があります。
最近では、画像認識に特化させた「FReLU」(Funnel Activation)も登場しています。
(3) Poolingレイヤ
脳の複雑型細胞をモデル化したもので、空間的な位置ずれを吸収し、同一形状と見なせるように機能します。データの次元削減を行なって、計算に必要な処理コストを下げる目的があります。
プーリングには学習という概念はなく粛々と決まった計算を行うのみです。
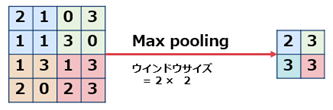
$ \hspace{15mm} 図 14 Max Poolingの例 $
上記はMax Poolingですが、これ以外にも平均を取るAverage Poolingがあります。

$ \hspace{15mm} 図 15 Average Poolingの例 $
(4) 全結合(Affine変換)
これまでの畳み込み演算とプーリングにより画像の特徴を得ましたが、特徴量を抽出するだけでは画像の識別はできません。識別には、「特徴量に基づいた分類」が必要です。この分類の役割を担っているのが、全結合層になります。得られたそれぞれの特徴量を1つのノードに集約し(各全結合層のノード数分実施)、活性化関数を通して出力します。具体的には隣接する層のすべての出力信号(データ)を結合します。このときに隣接する層のどのチャネルからどの程度の信号を受け取るべきなのか、(分類された結果と正解データの差から学習された)重み(w)およびバイアス(b)を使って計算していくことになります。
これを複数層重ね最終的に目的となる分類数のノード(数字であれば10ノード、画像識別であれば目的とする分類クラスの数)に出力して入力された特徴量が何なのかを予測することになります。
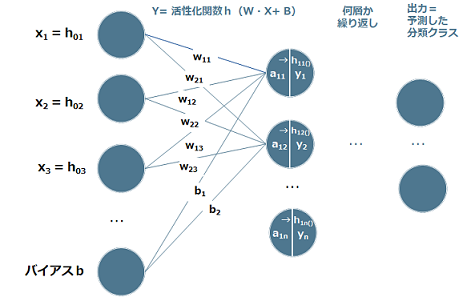
$$ 図\hspace{1mm}16 \hspace{30mm} $$
5.CNNの学習
学習の目的は畳み込み層や全結合層で用いる重み(やバイアス値)を学習データから自動で獲得することです。適切な重みやバイアスが学習で獲得できる=入力データが正しく分類されることになります。学習は以下のステップで行います。
- ステップ1 入力データの処理(ミニバッチ)
- ステップ2 各重みパラメータに関する損失関数の勾配を求める
- ステップ3 重みパラメータを勾配方向に微少量だけ更新する
- ステップ4 繰り返す
ここで「損失関数」とは、入力データに対しての正解ラベルと予測したデータとの差に
ここで「損失関数」とは、入力データに対する正解ラベルとモデルが出力した予測とのズレ(誤差)を数値化する関数です。一般には「二乗和誤差(MSE)」や「クロスエントロピー誤差」などがよく使われます。学習のイメージとしては、この損失関数で算出した損失を元に、出力層から入力層に向かって順に各層に勾配(微分値)を伝播させ、重み(フィルタ)を更新していきます。これを誤差逆伝播(Backpropagation)といいます。
$$ 図\hspace{1mm}17 \hspace{30mm} $$
(1) 損失関数
ⅰ) 2乗和誤差
モデルの出力 y と正解データ t をそれぞれ二乗し、その差分を誤差(損失)として返却する関数になります。
$$ E \hspace{3mm} = \hspace{3mm} - \frac{1}{2} \sum (y_{k} - t_{k})^{2} $$
ⅱ) クロスエントロピー誤差
自然対数eを底とするモデル出力値のlog値と正解データ値を乗算したものの総和を、損失とします。
$$ E \hspace{3mm} = \hspace{3mm} - \sum t_{k} \log_{y} K $$
自然対数log は、log に渡される x の値が 0 に近い時には絶対数の大きな出力になり、xの値が 1 に近いほど絶対数が 0 に近い出力になります。これは正解データ t が 1 の時にそれに対応するモデル出力予測yが 1 に近い数値を出力できていれば、tとxの乗算結果は小さくなり、xが 0 に近い誤った数値を出力していれば、tとxの乗算結果は大きくなるという論理です。
(2) 誤差逆伝播(Backpropagation)
ⅰ) 活性化関数
誤算逆伝播は順伝播の微分で表せられます。代表的な活性化関数の微分は以下になります。
① Sigmoid
$$ \frac{\partial{L}}{\partial{y}} ・ y(1 - y) $$
② ReLU
\begin{align}
\frac{\partial{y}}{\partial{x}} &= 1 \hspace{10mm} ( x > 0) \\
&= 0 \hspace{10mm} (x ≦ 0)
\end{align}
③ Softmax
$$ \frac{\partial{y}}{\partial{x}} = y_{n} - t_{n} ※tは正解ラベル $$
ⅱ) 畳み込み層
畳み込み層の誤差逆伝播は(畳み込み処理は関数ではないので)微分では算出できず、以下の流れになります。
-1 フィルタの値を縦横反転する
-2 出力1チャネルごとに畳み込み計算を行う
-3 各チャネルを合計する
- [補足]フィルタの値を縦横反転する
- 順伝播で関わった重みは以下のようになります。
- したがって、順伝播の重みを縦横反転したものを逆伝播に利用すれば良いことになります。
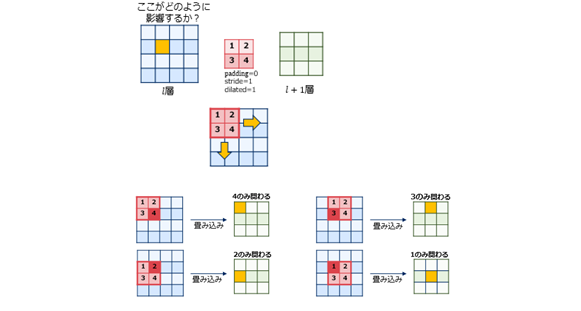
- [補足]出力1チャネルごとに畳み込み計算を行う、各チャネルを合計する
- 各層での計算は以下のようなイメージになります。
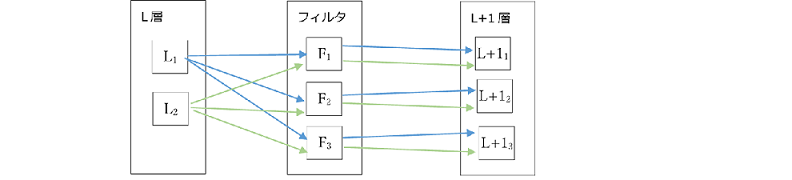
- 【順方向畳み込み】
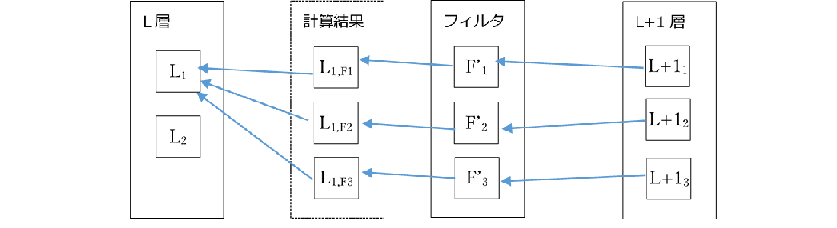
- 【逆方向伝搬※】
- 逆変換したフィルタを用いて畳み込む計算を行い、それらの結果を合計してもとのL層に戻します。なお、順方向畳み込みでゼロパディングやスライドを用いた場合は、それらを考慮してL+1層を拡大する必要があります。
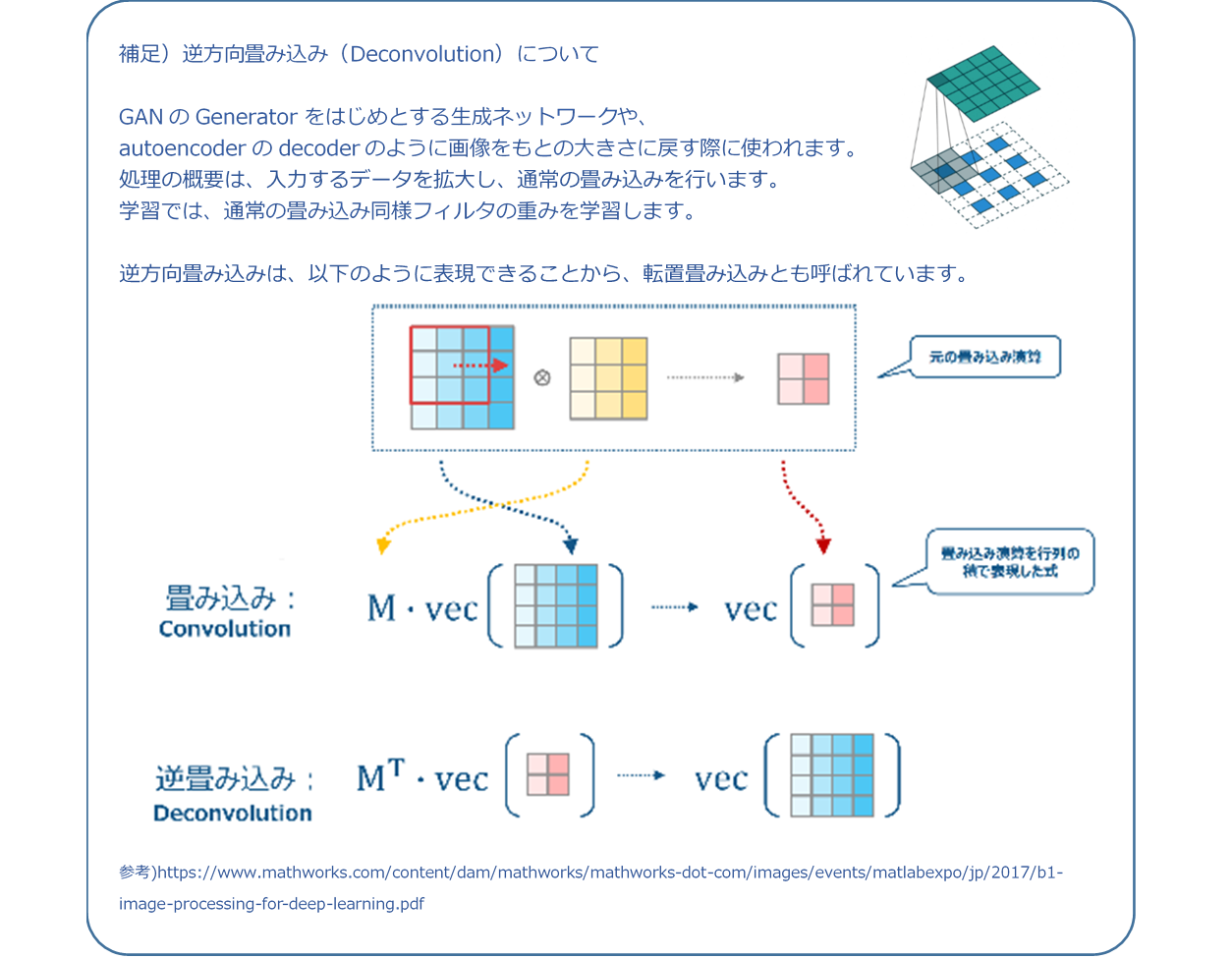
- ※下記補足にある画像をもとの大きさに戻す「逆方向畳み込み (Deconvolution)」と区別するため、「逆方向伝搬」という言葉を使っています
- ※F‘nは準方向でのフィルタの位置を逆に反転したもの
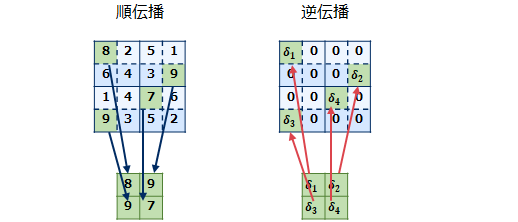
ⅲ) プーリング(最大プーリング)層
プーリング層はフィルタ情報がないので下層から伝播してきた誤差を更新して上層へ伝播します。 順伝播の際にウインドウサイズで選択した位置を覚えておき、逆伝播時には誤差を順伝播で選択した位置に分配しそれ以外のエリアにはゼロを設定します。
$$ 図\hspace{1mm}20 \hspace{20mm} $$
(3) 重みパラメータの更新方法(Optimizer)
学習時の重みを差分で一気に更新してしまうと1回のミニバッチ単位での学習結果が大きく反映されてしまうことになります。そのため、ミニバッチ単位で重みを徐々に更新していく手法が取れています。以下に主な手法を説明します。
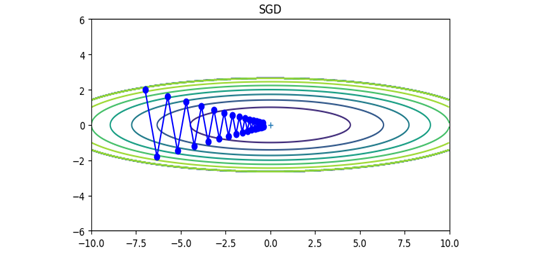
ⅰ) SGD(確率的勾配降下法)
ミニバッチとして無作為に選ばれたデータを使用して勾配降下を行う方法です。
W \hspace{4mm} \leftarrow \hspace{4mm} W - \eta \cdot \frac{\partial{L}}{\partial{W}}
※\hspace{2mm} \eta は学習係数。実際には0.01や0.001といった値を前もって決めて使用します
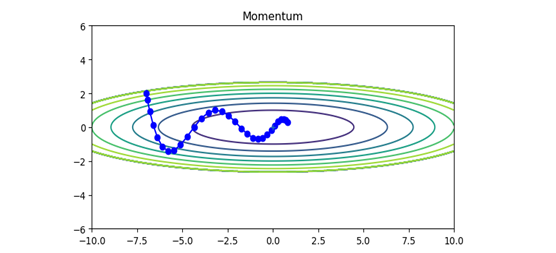
ⅱ) Momentum(モーメンタム)
SGDに 移動平均 を適用して振動を抑制したもの。SGDのジグザグな動きを軽減することができる。
\begin{align}
v \hspace{4mm} &\leftarrow \hspace{4mm} \alpha v - \eta \cdot \frac{\partial{L}}{\partial{W}} \\
W \hspace{4mm} &\leftarrow \hspace{4mm} W + v
\end{align}
$$ 図\hspace{1mm}22 \hspace{20mm} $$
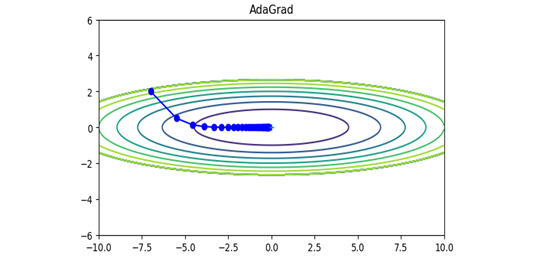
ⅲ) AdaGrad
学習係数ηの減衰(学習が進むにつれて学習係数を小さくすることで最初は大きく、次第に小さく学習する)する手法です。過去の勾配を2乗和としてすべて記録しています。
\begin{align}
h \hspace{4mm} &\leftarrow \hspace{4mm} h + \frac{\partial{L}}{\partial{W}} \odot \frac{\partial{L}}{\partial{W}} \\
W \hspace{4mm} &\leftarrow \hspace{4mm} W - \eta \cdot \frac{1}{\sqrt{h}} \cdot \frac{\partial{L}}{\partial{W}} \\
\end{align}
$$図\hspace{1mm}23 \hspace{10mm} $$
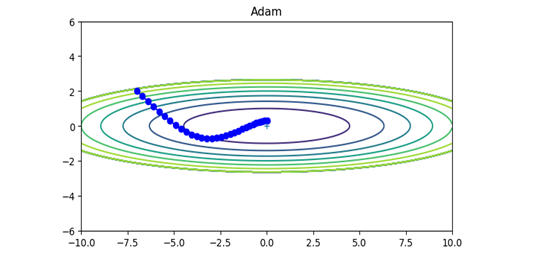
ⅳ) Adam
MomentumとAdaGradを融合したような手法です。
\begin{align}
m_{t+1} &= β_1m_t + ( 1 - β_1 ) ∇E(w^t) \\
v_{t+1} &= β_2v_t + ( 1 - β_2 ) ∇E(w^t)^2 \\
\hat{m} &= \frac{m_{t+1}}{1-β_1^t} \\
\hat{v} &= \frac{v_{t+1}}{1-β_2^t} \\
w^{t+1} &= w^t-α\frac{\hat{m}}{\sqrt{\hat{v}}+ε} \\
\end{align}
ⅴ) RMSProp
AdaGradを改良したアルゴリズムです。指数関数的に過去の勾配情報を忘れ、より直近の勾配情報を優先する手法です。
\begin{align}
h_t &= αh_{t-1}+(1-α)∇E(w^t)^2 \\
\eta_t &= \frac{\eta_0}{\sqrt{h_t}+\epsilon} \\
w^{t+1} &= w^t- \eta_t E(w^t) \\
\end{align}
ⅵ) その他
Momentumの改善版のNAG(Nesterov(ネステロフ)の加速勾配法)など改良された手法が次々に登場しています。
多くのモデルでは今でもSGDが使われてきましたが、最近ではAdamが多く使われています。ただし、すべてのモデルで優れた手法というものはなく、それぞれの手法(扱うデータにもよる)で得意・不得意があり、実際には学習して評価してみる必要があります。
(4) パラメータの初期値
ニューラルネットワークの学習で重みの初期値は特に重要になります。以下に2つの初期値について説明します。
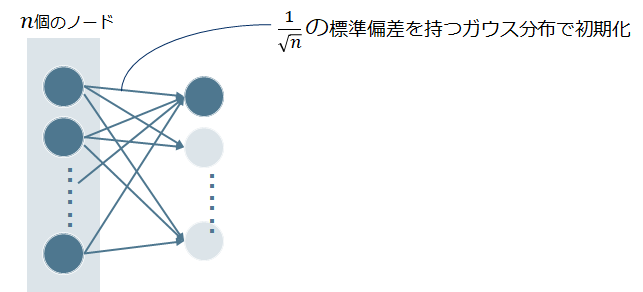
ⅰ)Xavierの初期値
前層のノード(ニューロン)数をnとした場合、1/√nの標準偏差を持つ分布を使います。活性化関数が線形であることを前提に導いたもので、sigmoid関数やtanh関数が適しています。
ⅱ) Heの初期値
前層のノード(ニューロン)数をnとした場合、√2/nの標準偏差を持つ分布を使います。ReLUに特化した初期値であり、ReLUの場合は負の領域がゼロになるため、より広がりを持たせるために2倍の係数を持たせたものです。
6.付録
(1)過学習
ⅰ) 正則化(Regularization)
機械学習では、過学習(overfitting)が発生することがあります(下図のように)。過学習とは訓練データに過度に適応しすぎてしまい、訓練データ以外のデータには対応できない状態(=正しく識別できない)を指します。過学習を抑止するためのテクニックを正則化といい主に下記の対応方法があります。
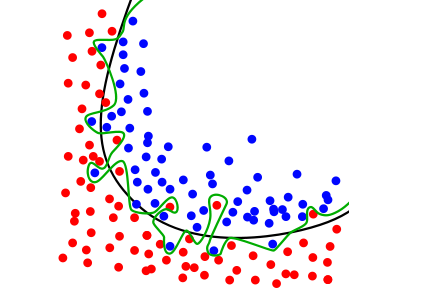
$$図\hspace{1mm}26 \hspace{50mm} $$
- Weight decay(荷重減衰)
すべての重みに対して、損失関数に1/2λW2(L2ノルム)を加算し、大きな重みを持つことに対してペナルティを与えることで過学習を抑止します。また、誤差逆伝播法による勾配の伝播はこの微分であるλWが伝わることになります。
ⅱ) 正規化(Normalization)
正規化とは、特徴量の値の範囲を一定の範囲におさめる変換になります。主に[0, 1] か、[-1, 1]の範囲内におさめることが多いです。
例えば、[0, 1]におさめるとすると、特徴量CNNxのi番目の値の変換の式は以下になります。
x_{norm,i}=\frac{x_i-x_{min}}{x_{max}-x_{min}} \\
xnormが正規化された x になります。xminは x の最小値、xmaxは x の最大値です。
これを計算することで、正規化する前の特徴量の最小値は正規化されて0に、最大値は1となり、新しい特徴量は [0, 1] におさまります。
ノーマライズには以下の類似的な処理があります。 いずれもバッチノーマライズと処理方法は同じで、1度に正規化する範囲が異なるだけになります。
①バッチノーマライズ:は学習を速く進行させることができ、初期値にそれほど依存せず学習を抑制する(Dropout などの必要性を減らす)効果があります
②Layerノーマライズ:1つのデータの全チャネルに対して正規化を行う
③Instanceノーマライズ:1つのデータの1つのチャネルに対して正規化を行う
④Groupノーマライズ:上記の中間で1つのデータの任意のチャネル数に対して正規化を行う
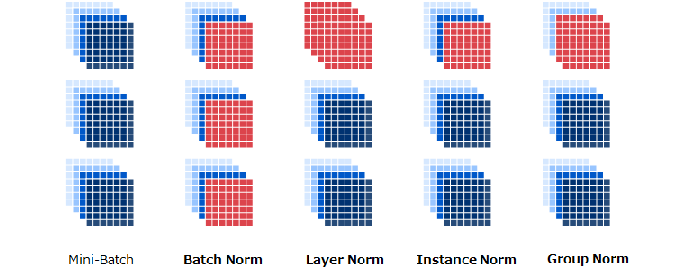
$$ 図\hspace{1mm}27 $$
通常はバッチノーマライズを使用しますが、以下のモデルではそれぞれ以下のノーマライズが使われています。
- RNN系やTransformerモデル : Layerノーマライズが多く使われている
- GAN系モデル : Instanceノーマライズが多く使われている
- 画像認識系モデル : グループノーマライズが使われている
ⅲ) Dropout
ニューラルネットワークモデルが複雑になると、Weight decayだけでは過学習防止は困難になってきます。 そのため、Dropout(文献XXXX)を用います。 Dropoutは、学習時にニューロンをランダムに選び出し、その選び出したニューロンを消去して学習します。 また、テスト時にはすべてのニューロンを使用しますが、各ニューロンの出力に対して、訓練時に消去した割合を乗算して出力します。
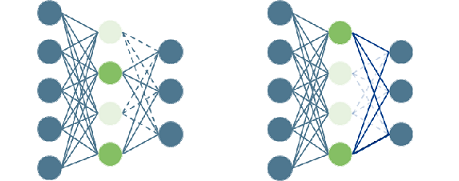
$$ 図\hspace{1mm}28 \hspace{50mm} $$
7.おわりに
CNNをマスタすることは、今後様々なモデルを学習・理解する基礎になると思います。記載誤り・不足等がありましたら追記して、できる限り正確かつ分かりやすくしていきたいと思います。