強化学習DQN（Deep Q-network）

本書は筆者たちが勉強した際のメモを、後に学習する方の一助となるようにまとめたものです。誤りや不足、加筆修正すべきところがありましたらぜひご指摘ください。継続してブラッシュアップしていきます。
© 2021 NPO法人AI開発推進協会

本書は深層強化学習でもっとも基本的なDQNについて説明します。(CNNの基礎を理解している前提で記載しています。まだ理解していない方は別冊のCNNの基礎を先に読んでください）

１．強化学習の基礎

強化学習は、認知した情報から行動を判断するための学習手法です。強化学習では、正解データをもとに学習するのではなく、行動に対するフィードバックを「報酬」として間接的な評価（どの程度良かったのか）をもとに学習します。そのため、強化学習は、試行錯誤しながら最適な行動を学習する手法といえます。

図 1　DQNのアーキテクチャ

　

強化学習のアルゴリズムの代表的な分類に、価値学習／方策学習、モデルフリー／モデルベースがあります。DQNは、「マルコフ決定過程」や「ベルマン方程式」を用いたQ-Learning（後述で詳しく解説）をベースにDNNを適用したアルゴリズムです。

２．マルコフ決定過程 （Markov Decision Process : MDP）

図 2　フルーツキャッチゲームにおける状態の変化

　
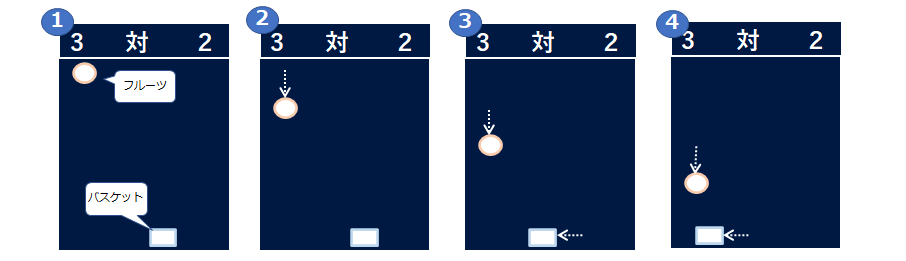
時刻tにおける環境の状態をst（＝上図２の①～④のそれぞれ）において、エージェント（上図ではバスケット）は特定の行動atを取ることができます（この場合は、左へ移動、右へ移動、そのままとどまる）。この行動に応じて、正または負（ゲームスコアの増減等）の報酬rtが与えられます。エージェントが行動をとることで環境は変化して次の状態St+1遷移します。　そしてエージェントはat+1を取って次の状態に遷移することを繰り返していきます。この状態、行動、報酬のセットは状態のルールとともにマルコフ決定過程を構成し、マルコフ決定過程では、状態St+1へ遷移する確率は、現在の状態Stとそこでの行動atのみに依存します。

強化学習の目的は、エージェントが各エピソード（１ゲーム）で獲得する報酬（r）の総和を最大にすることですが、報酬の総和Ｒは以下の式になります。
　　　R_t = Σr_i　= r_i+ r_i+1 + ・・・ + r_n

ただし将来の報酬は不確定であり、割引率（γ）を将来の報酬ほど掛けて報酬を割り引きます。
　　　Rt = r_t + γr_t+1 + γ²r_t+2 + ・・・ + γ^n-tr_n
　　　　 = r_t + γ(r_t+1 + γ(r_t+2 + ・・・ ))
　　　　 = r_t + γR_t+1
　　　　※次の時刻における割引現在価値の総和をRt+1にすることで再帰的に計算が可能

３．Q-learning

Q-learningは有限のマルコフ決定過程のある状態sにおいて最適な行動aを見つけるための手法で、割引現在価値をＱ関数の出力という形で定義します。
　　　Q(s_t, a_t) = max(R_t+1)

また、任意な状態において最適な行動を選択する戦略πは、Ｑ関数の出力値が最も高い行動になるので以下のようになります。
　　　π(s) = arg max_aQ(s, a)

さらに時刻tにおけるＱ関数は、割引現在価値Rt、Rt+1と同様に再帰的に記載すると下記の式となり、これをベルマン方程式（Bellman equation）と言います。
　　　Q(s_t, a_t) = r + γmaxQ(S_t+1, a_t+1)

Q関数の出力は状態sで行動aをとったときの価値(Q(s, a))の見込みを出力するものですが、これを縦軸に状態s、横軸に行動aをとって表にしたものをQ-tableと呼びます。

Q-tableの更新の流れは以下のようになります。

　① Q-tableをランダムな値で初期化する
　②～④を繰り返す
　　② 行動aを実施、報酬を得る
　　③ ベルマン方程式から状態sにて行動aをとった場合の「Ｑ(s, a):割引現在価値」を計算し、Q-tableの該当セルを更新する
　　④ 遷移した状態s’で行動a’を選択して実行する

③の更新は、実際の報酬と予測との差に学習率をかけて更新します。
具体的には、
　　　Q(s, a) = Q(s, a) + η(r + γmaxQ(S_t+1、 a_t+1) – Q(s, a))　　※ηは学習率

となります。これはSGD(確率的勾配降下法)に近い形式（W = W – η・∂L/∂W）になり、誤差は「r + γmaxQ(S_t+1、 a_t+1) – Q(s, a)」で表され、実際の報酬と予測との差になります。この更新処理を繰り返すことで学習をしていきます。

４．Deep Q-Networkの特徴

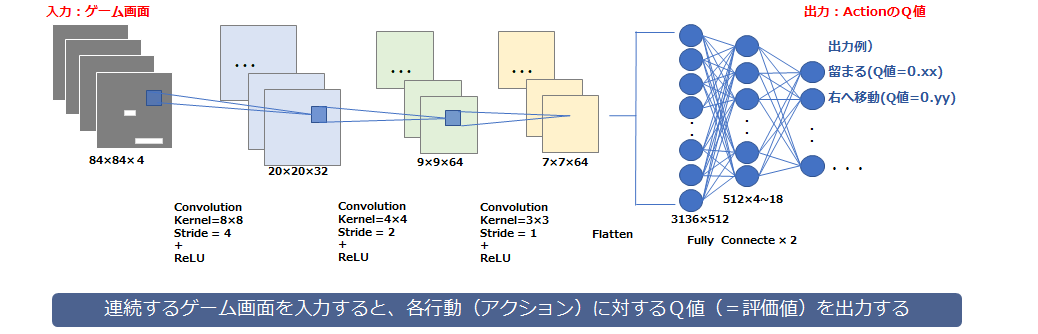
DQNは、google社の子会社のDeepMind社が開発したアルゴリズムです。画像認識に多く用いられる深層学習と強化学習(Q学習)を組み合わせたアルゴリズムにより動作します。

(1) モデルの構成

３つの畳み込み層と２つの全結合層を使用しています。プーリング層はもとの情報を圧縮してしまい表示しているオブジェクトの位置を認識しづらくするため、使用されていません。

(2) 探索と活用のバランス

学習の最初はなるべく新規のデータを使ってランダムな行動をすることが学習パフォーマンスの向上につながります。これを実現するシンプルな方法として「ε-greedy法」があります。εの確率でランダムに行動し、1 – εの確立でネットワークモデルの学習結果を採用して行動します。そして学習が進むほどＱ関数の値は信頼性が増してくるためεの値を下げていきます（DeepMindの論文では1から0.1まで徐々に下げていく）。

多く探索した方が正確なＱ関数が得られますが、その分学習成果を生かせなくなり、その逆も同様でありこれらはトレードオフの関係にあります。 ε-greedy法を利用することで少ないパラメータによりこのトレードオフを調整することが可能になります。

(3) Experience Replay

連続するフレームでは差分が少ない似たような画面でありこれで学習させてもほとんど似たような画面を出力するようになってしまいＱ関数の学習もうまくいきません。このため、学習中の行動結果（s, a, r, s’）をメモリ（replay memory）に格納し、学習を行う際はこのメモリからランダムにフレームを抽出してバッチを作成して似たような画面が連続することを防ぎながら実施します。この手法をExperience Replayといいます。

(4) Q-networkの固定

Q関数の更新には、Q(s’, a’)という次の状態における報酬の期待値が必要になりますが、前述のように回帰的に実施するため、更新した瞬間にQ(s’, a’)に値も変わってしまい（教師あり学習で言えば教師データが変わることと同等）、学習がうまくいきません。このため、Q(s’, a’)の算出にいついては一定期間重みを固定します。これにより正しいQ(s’, a’)は得られませんが、同じ条件では同じ値を返すようにネットワークを固定することで学習を安定させることができます。この手法をQ- networkの固定といいます。ある程度学習が進んだら重みを更新してしばらくは固定して学習することを繰り返していきます。

(5) 報酬のクリッピング

報酬の値を固定（ex　成功は１、失敗は-1）して学習します。これにより学習が行いやすくなります。

５．おわりに

以上が強化学習ＤＱＮの概要になりますが、記載したとおり理論そのものはそれほど難しいものではありません。