はじめに
DataRobot で小売・流通業のお客様を担当しているデータサイエンティストの新名庸生です。
ビジネスにおいて機械学習を活用する際、予測ターゲットに対し各特徴量がどのような関係性を持っているのかというインサイトが求められることが多々あります。これは、要因分析のような、インサイト獲得自体が目的であるような場合はもちろん、扱うモデルを解像度高く理解し、自信を持って予測値を利用するためにも必要なプロセスです。
その際、よく活用されるDataRobotの機能として「特徴量ごとの作用」というチャートがあります。DataRobotの過去のブログでも解説されているように、「特徴量ごとの作用」の「部分依存」を見ることで、特定の特徴量の値の変化と予測ターゲットとの関係性をひと目で確認することができます。部分依存はPDP(Partial Dependence Plot)などとも呼ばれるモデルの解釈手法です。
ただ、一般的な統計的因果推論の手法と同様に、機械学習を用いた分析においても、扱っている特徴量間の関係性に注意しないと、誤ってバイアスが生じている部分依存を解釈してしまうことがありますので、本ブログにおいてはそのポイントを解説したいと思います。
注意が必要なケース
まず結論からまとめます。簡単のために、以下の3変数のみを扱う場合を考えます。
- Y:結果(予測ターゲット)
- T:処置(部分依存で予測ターゲットとの関係性を確認したい特徴量)
- C:共変量(Y, Tと関係する特徴量)
この3変数の因果関係を有向非巡回グラフ(DAG)を用いて因果グラフとして表現したとき、部分依存にバイアスを生じさせないためには、以下のような必要があります。
- Cが分岐点の場合はCを特徴量として機械学習モデルに追加する必要がある。
- Cが合流点、あるいは中間点である場合はCをモデルから除外する必要がある。
すなわち、正しく部分依存を確認するには、まずドメイン知識にもとづいた因果グラフを事前にきちんと表現できている必要があります。
それぞれについて以下で具体例を用いながら見ていきます。なお、ここでの具体例の一部は文献[1]を参考にしています。
また、あくまでもこれは部分依存を正しく見るためであり、精度の良い予測値を算出するためであれば後者においてもCはモデルに追加するのが望ましいことも改めて後述します。
Cが分岐点の場合
150人分の患者に対し、患者の年齢層と、特定の薬の投薬量とその後の症状の悪さを表したデータがあります。これを散布図でプロットすると以下のようになり、一見、投薬量が多いほど症状が悪くなっているように見受けられます。
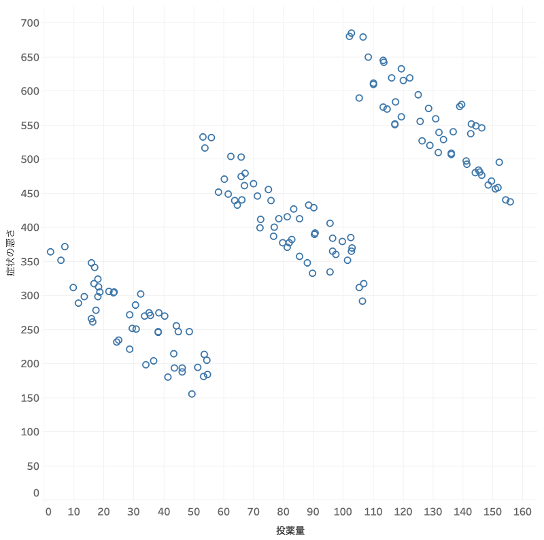
図2: 投薬量と症状の悪さの関係(各丸は患者)

図3: 投薬量と症状の悪さと年齢層の関係(オレンジ:若年、赤:中年、青:高齢)
ただ、ここで患者の年齢層を色で表現すると図3のようになり、若年層、中年層、高齢層それぞれで見ると投薬量が多いほど症状が軽くなっていることがわかります。(このように、全体の傾向が、部分で見た場合の傾向と異なるケースは「シンプソンのパラドックス」として度々取り上げられます。)
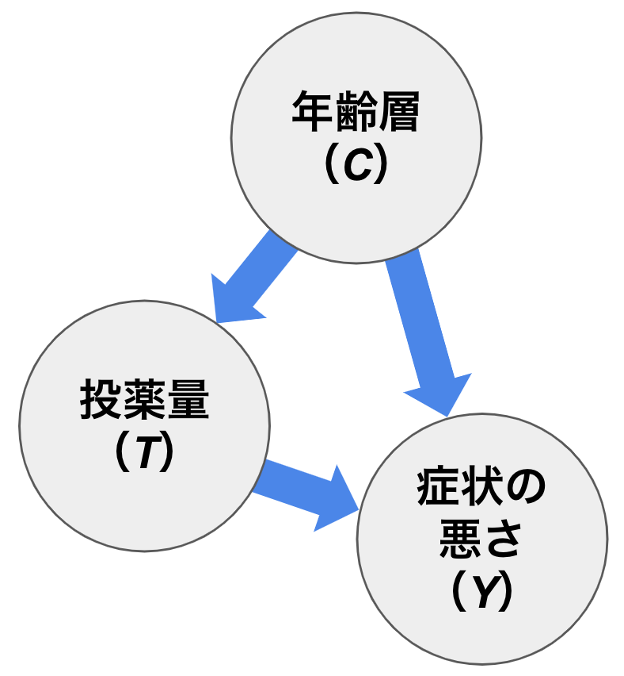
この例における3変数の因果関係をDAGで表現すると、以下のように患者の年齢層が分岐点になっているとします。この前提はデータ自体からは判断できず、ドメイン知識に基づく必要があります。(ちなみに文献[1]では、「シンプソンのパラドックス」が長年「パラドックス」として扱われてきた原因として、ドメイン知識に基づく因果構造の概念が伝統的な統計学に不在であったこと挙げています。)
「投薬量」と「症状の悪さ」の裏には双方に影響を与える「年齢層」が存在しており、「症状の悪さ」を「投薬量」だけで解釈しようとすると、「年齢層」の影響がバイアスとして入り込んでしまいます。
つまり、仮に
- 症状の悪さ=β投薬量+γ年齢層 (式1)
と表現されるものを
- 症状の悪さ=β’ 投薬量 (式2)
という式で表現してしまうと、β’に本来ないバイアスがかかってしまいます。具体的には、図3から明らかなように、(式1)のβは負の係数であるのに、(式2)のβ’は正の係数となってしまいます。このようなバイアスの発生を回避するには、各年齢層ごと(若年、中年、高齢)に分けるか、(式1)のように「年齢層」を特徴量に追加して扱う必要があります。
実際にDataRobotの部分依存でも確認してみましょう。

図5: 「年齢層」と「投薬量」を特徴量としたモデルの「投薬量」の部分依存
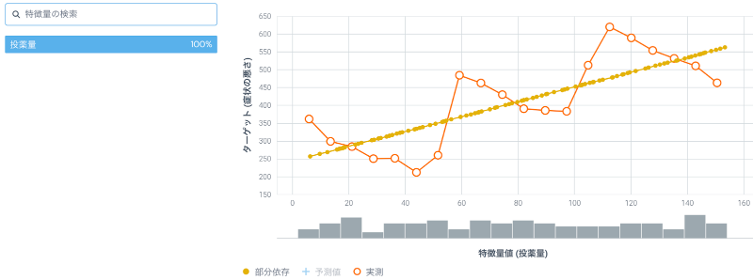
図6: 「投薬量」のみを特徴量としたモデルの「投薬量」の部分依存
「投薬量」と「年齢層」を投薬量として加えた場合は、「投薬量」の値が大きくなるほど「症状の悪さ」の値は小さくなる負の相関となっています(図5)。一方、「投薬量」のみを特徴量とした場合の部分依存を見ると、「投薬量」の値が大きくなるほど「症状の悪さ」の値も大きくなる正の相関となっています(図6)。これは(式2)の、バイアスがかかった関係性に相当します。
これが、「Cが分岐点の場合はCを特徴量として機械学習モデルに追加する必要がある」の具体例です。イメージを掴んでいただければ幸いです。
Cが合流点の場合
同様にCが合流点の場合の具体例も見てみましょう。
ある美術大学の入学試験の200名分のデータを考えます。入学試験には学科試験と実技試験があり、それぞれ100点満点です。合格基準は学科試験と実技試験の平均が50点以上であることです。
「学科試験」「実技試験」「合否」の3変数をそれぞれT, Y, Cとし、その関係性を因果グラフで表現すると以下のようになり、「合否」は合流点となります。
この200名のデータは以下のようになっています。
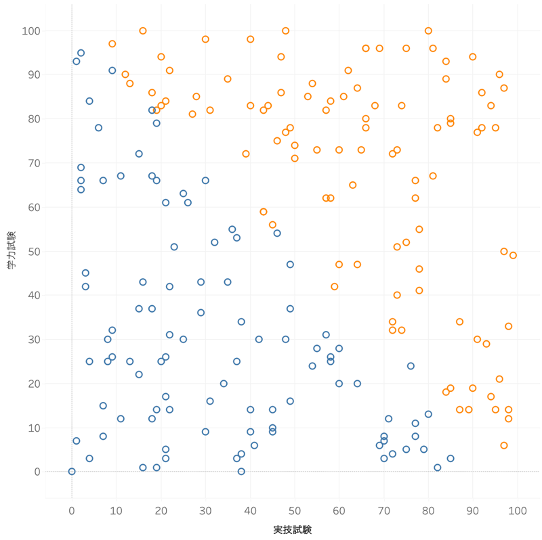
図8: 実技試験結果、学力試験結果と合否の関係(各丸は学生、オレンジ:合格、青:不合格)
こちらを見て分かるように、実技試験と学力試験の点数の間には相関はありません。(実際、それぞれの点数は乱数から生成しています。)
このデータで実技試験を予測ターゲットとし、DataRobotでモデリングしてみた結果を以下に示します。
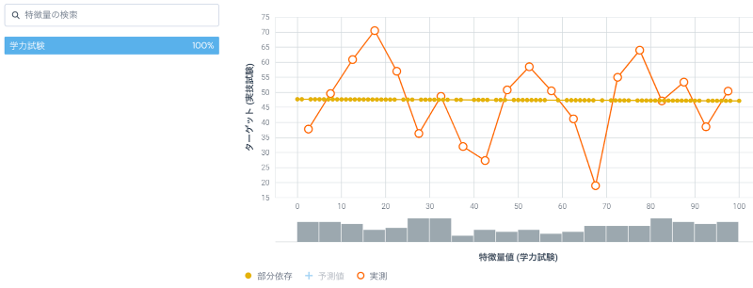
図9: 「学力試験」のみを特徴量としたモデルの「学力試験」の部分依存(モデル精度 RMSE:29.0)

図10: 「学力試験」と「合否」を特徴量としたモデルの「学力試験」の部分依存(モデル精度 RMSE:21.0)
まず、特徴量として「学力試験」のみを用いた場合、特徴量ごとの作用を見ると学力試験の結果が変化しても実技試験の結果には変化がないというグラフになっています(図9)。これは今回のデータの作り方から見ても納得感があります。
一方、特徴量に「学力試験」だけでなく、「合否」も入れてモデリングした場合の特徴量ごとの作用を見てみましょう。すると、学力試験の点数が高くなるほど実技試験の点数が低くなるようなグラフになっていますが、これは事実ではありません(図10)。
特徴量ごとの作用は、他の特徴量(この場合は「合否」)は固定したまま、現在着目している特徴量(この場合は「学力試験」)の値を変化させたときに予測値がどの様に変化するかを表していますので、「合否」を特徴量として加えた場合、合否結果が分かった前提で学力試験と実技試験の関係性を特徴量ごとの作用で示すことになります。
もし合格している場合、学力試験の点数が低ければ実技試験の点数は高いはずですし、不合格の場合は学力試験の点数が高ければ実技試験の点数は低いはず、ということになり、図10のような部分依存になっています。
すなわち、特徴量ごとの作用を正しく見るためには合流点となる特徴量は除いてモデリングする必要があるということになります。
ただ、注意が必要なのは、精度を求めるモデリングをする際には情報量が多いに越したことはありませんので、「合否」も特徴量として含めたほうが良いです。実際、図のタイトルにもあるように、合否を特徴量として入れた場合の方がRMSEは小さくなっています。
ここから、精度高く予測するためのモデリングと、バイアスなく部分依存を確認するためのモデリングには手法に差があることが分かります。
Cが中間点の場合
Cが中間点の場合の具体例も見てみましょう。
複数のエリアで、在来種Aの個体数を守るために外来種Bの駆除を行っているとしましょう。外来種Bの駆除にどれだけ力を入れるかの段階があり、その力の入れ具合で外来種Bの根絶が成功するか、失敗するかが変わってくるとします。
このとき、外来種Bの駆除努力、外来種Bの根絶、在来種Aの個体数をそれぞれT, C, Yとすると、3変数の関係性は以下のような因果グラフで表現でき、外来種Bの根絶(C)は中間点となります。
図11: 外来種Bの駆除努力、外来種Bの根絶(根絶できたか否か)、在来種Aの個体数の因果グラフ
在来種Aの保護のための外来種Bの駆除を400エリアで行ったデータを以下のように作成しました。
外来種Bの駆除努力と在来種Aの個体数はそれぞれ0から15までの数字で段階づけされており、外来種Bの根絶が成功したエリアはオレンジ、失敗したエリアは青でプロットされています。(色の濃さは複数のデータの重なりによって変化しています。)
「外来種Bの駆除努力」の値が大きいほど「外来種Bの根絶」は成功しており、「在来種Aの個体数」も大きくなる傾向があることが分かります。
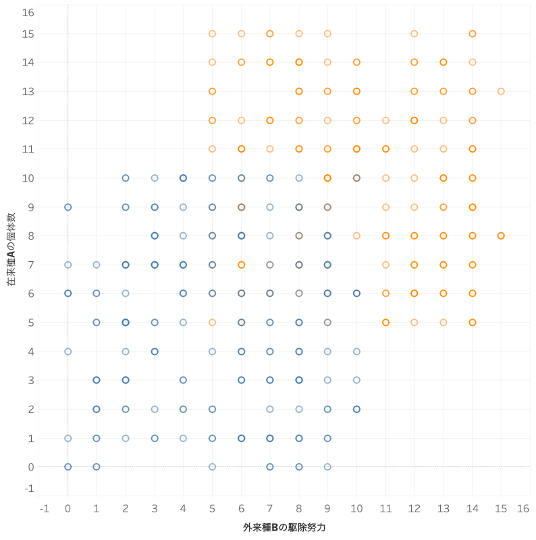
図12: 外来種Bの駆除努力、外来種Bの根絶、在来種Aの個体数の関係(各丸はエリアごとの取り組みデータ、オレンジ:外来種Bの根絶成功、青:外来種Bの根絶失敗)
このデータで「在来種Aの個体数」を予測ターゲットとしてモデリングしてみた結果を以下に示します。

図13: 「外来種Bの駆除努力」のみを特徴量としたモデルの「外来種Bの駆除努力」の部分依存(モデル精度 RMSE:3.61)
図14: 「外来種Bの駆除努力」と「外来種Bの根絶」を特徴量としたモデルの「外来種Bの駆除努力」の部分依存(モデル精度 RMSE:2.93)
「外来種Bの駆除努力」のみを特徴量として用いた場合、この値が大きいほど「在来種Aの個体数」も大きくなる関係性が部分依存から読み取れます(図13)。
一方、特徴量に「外来種Bの根絶」も加えた場合、「外来種Bの駆除努力」の部分依存はほぼ横ばいで、駆除努力の大小は、在来種Aの個体数と関係がないように見受けられますが、これは事実ではありません(図14)。
これも前述の「Cが合流点の時」と同様、C(外来種Bの根絶)の値が与えられた状態で「外来種Bの駆除努力」と「在来種Aの個体数」の関係性を計算することになるので、このように正しくない部分依存グラフとなってしまいます。
部分依存を正しく見るためには、中間点となる特徴量は除いてモデリングする必要があるということになります。(合流点の場合と同様、特徴量に加えたほうが精度としては上がります。)
因果仮説を機械学習の部分依存で検証する際の落とし穴のまとめ
冒頭に記載したように、バイアスなく部分依存を確認するには
- Cが分岐点の場合はCを特徴量として機械学習モデルに追加する必要がある
- Cが合流点、あるいは中間点である場合はCをモデルから除外する必要がある
ということを具体例を用いて見てきました。
今回は簡単のため3変数に絞った例を見てきましたが、この考え方は4変数以上にも拡張することができます。このとき、どの変数を特徴量として加えるべきか、特徴量から除外すべきかを決定するのが「バックドア基準」になります。この記事ではバックドア基準の詳細には触れませんが、関心のある方は是非文献[1]などをご参照ください。
もしかしたらこれまでに作成してきたモデルにおいて、部分依存グラフが想定した形になっていないという経験をされた方も多いかも知れません。その場合は是非、上記の観点からデータを振り返って見ると良いかもしれません。
皆さまのデータ分析のご参考になれば幸いです。
参考文献
- 林岳彦(2024)『はじめての統計的因果推論』岩波書店