この記事の内容
この記事では二分探索と三分探索の解説及びその実装について記します。
この記事の特徴として数学的に厳密な説明を心がけているので、直感的な説明を読みたい場合は参考記事を見るなどするようにお願いします。
前置き
以下では二分探索(or三分探索)で考える関数の定義域xを整数または実数の集合上での閉区間としますが、実際には全順序集合(有理数の集合などを含む)上での閉区間であれば定義域とすることができます。
また、パソコン上においては実数のような連続集合であっても離散的に扱うので、以下の集合は全て離散集合であることに注意が必要です。
二分探索
二分探索とは
x(元の個数は$n$)で単調増加(or減少)関数$f$が定義されている時、$f(x^*)=t$となる$x^* \in$ xが存在するかを$O(\log n)$で探索するアルゴリズムのことです。1
以下では暗黙的に$f$を単調増加関数としていますが、不等号を逆向きにするなどの工夫をすれば$f$が単調減少関数であっても同様の議論をすることができます。
二分探索では関数$f$が定義された探索領域を$\frac{1}{2}$していくことで高速に最小値を探しますが、以下のような仮定(✳︎)のもとで$\frac{1}{2}$していくので(✳︎)を示します。
(✳︎)
閉区間$[l,r]$での$f(x^*)=t$となる$x^* \in [l,r]$について、$[l,r]$の二等分点を$k$としたとき
$f(k) \geqq t \rightarrow x^* \in [l,k]$ かつ $f(k) < t \rightarrow x^* \in (k,r]$
証明
(1)$f(k) \geqq t$のとき
$f(k) \geqq t \leftrightarrow k \geqq x^*$($\because f$ は単調増加関数)
よって、$x^*$は$[l,k]$に含まれる。
(2)$f(k) < t$のとき
$f(k) < t \leftrightarrow k < x^*$($\because f$ は単調増加関数)
よって、$x^*$は$(k,r]$に含まれる。
よって(1),(2)より(✳︎)は示される。
$[Q.E.D.]$
また、$false$を$0$,$true$を$1$とすれば、返り値がbool値で$x^* \in$ xを境に$false$と$true$が入れ替わるような関数を考えることができ、境になる$x^*$を同様のアルゴリズムで求めることができます。
二分探索の実装
二分探索の具体的な実装を以下に載せます(コード上のコメントアウトが実装で役に立つと思います。)。
また、実装を確認するのが目的なので扱った問題の解説はこの記事ではしませんが、二分探索の理解を深めるには問題を一度解くのがおすすめです。
①関数の戻り値がbool値でない場合
ソート済の配列の要素で$k$となる要素を探す際に良く用いられます。定義域xをインデックスの集合で関数の戻り値をそれぞれのインデックスに対応する配列の要素と考えれば確かに単調な関数$f$を定義域xで定義できていることがわかります。また、ソート済の配列から$k$を探す場合はbisectモジュールを使うと自分で二分探索を実装せずに済みます。詳しくはこの記事を参照してください。
ここでは、配列$a=[0,1,1,2,4,5,6,8,8,9,10]$から2となる要素のインデックスを二分探索で探してみます。
a=[0,1,1,2,4,5,6,8,8,9,10]
# 二分探索のコード
# (1)l,rは両端点でl<=r
# インデックスlが2より小さくrが2以上であることを確認する。
l,r=0,10
# (2)l=rもしくはl=r-1のときにbreak
while l+1<r:
#(3)その閉区間の中点(の小数部分を切り捨てたもの)
#オーバーフローを考慮すると以下の書き方になる
k=l+(r-l)//2
#(4)閉区間の分割
#a[k]>=2の場合は大きい方の端点をkにし、a[k]<2の場合は小さい方の端点をkにする
if a[k]>=2:
r=k
else:
l=k
# (5)出力
# rはa[x]>=2となるインデックスのうち最小(a[x]=2となるインデックスxが存在するとは限らないことに注意)
print(r)
②関数の戻り値がbool値である場合
自分で二分探索を実装する場合はこちらのパターンの場合がほとんどかと思います。以下では、ABC063D-Widespreadを題材にコードを書いており、関数$f$の戻り値を$true$にするようなxのうち最小のものを求めています。
また、この問題の解き方を知りたい場合は本解や僕の解説記事を参照してください。
import math
n,a,b=map(int,input().split())
h=[int(input()) for i in range(n)]
def f(x):
global n
c=0
for i in range(n):
if h[i]-x*b>0:
c+=math.ceil((h[i]-x*b)/(a-b))
return c<=x
# 二分探索のコード
# (1)l,rは両端点でl<=r
# この際lでは偽でrでは真になることを確認する
l,r=0,10**9
# (2)l=rもしくはl=r-1のときにbreak
while l+1<r:
#(3)その閉区間の中点(の小数部分を切り捨てたもの)
#オーバーフローを考慮すると以下の書き方になる
k=l+(r-l)//2
#(4)閉区間の分割
#x=kで真の場合は大きい方の端点をkにし、x=kで偽の場合は小さい方の端点をkにする
if f(k):
r=k
else:
l=k
# (5)出力
# rはf(x)=真となるxのうち最小
print(r)
三分探索
三分探索とは
以下の凸or凹関数は全て狭義であることに注意してください!
そのため、一部の記述に間違いがありますが、適宜読み替えてください
x(元の個数は$n$)で擬似凸(or凹)関数$f$が定義されている時、$f(x)$が最小(or最大)となる$x^* \in$ xを$O(\log n)$で探索するアルゴリズムのことです。また、xは有限集合であるために必ず最小点(or最大点)を持ちます。
以下では暗黙的に$f$を擬似凸関数としていますが、不等号を逆向きにするなどの工夫をすれば$f$が擬似凹関数であっても同様の議論をすることができます
ここで、擬似凸関数は以下のように定義されます。2
$^∀ x_1,x_2 \in$ x,$^∀ \lambda \in [0,1]$に対して$\lambda x_1+(1-\lambda)x_2 \in$ xならば、$f(\lambda x_1+(1-\lambda)x_2) \leqq \lambda f(x_1)+(1-\lambda)f(x_2)$が成り立つ。
三分探索では関数$f$が定義された探索領域を$\frac{2}{3}$していくことで高速に最小値を探しますが、以下のような仮定(✳︎)のもとで$\frac{2}{3}$していくのでこれを示します。
(✳︎)
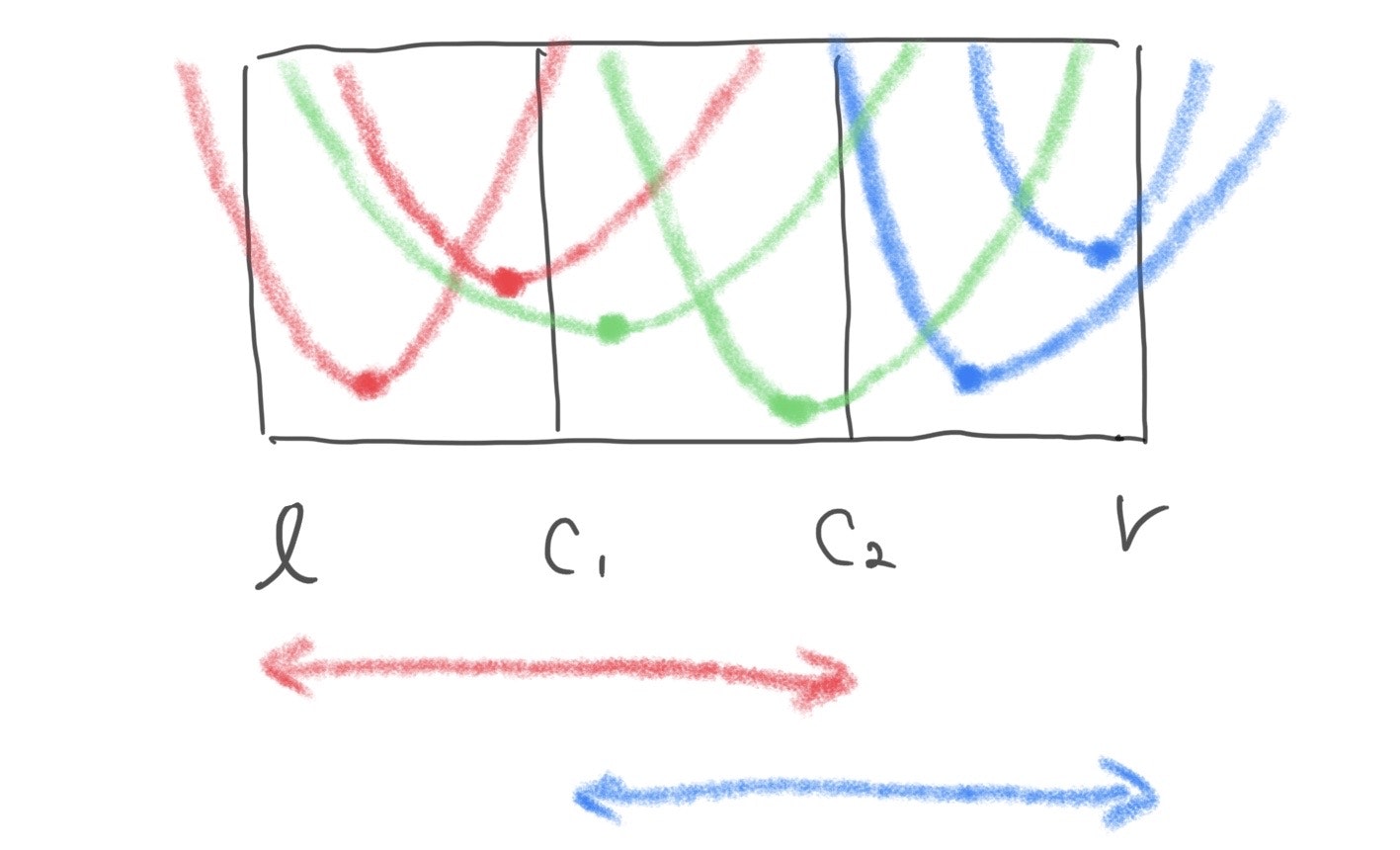
閉区間$[l,r]$での最小点$x^* \in [l,r]$について、その区間の三等分点を$c_1,c_2(l \leqq c_1 \leqq c_2 \leqq r)$としたとき、
$f(c_1) \leqq f(c_2) \rightarrow$最小点$x^*$は$[l,c_2]$に含まれる。
$f(c_1) \geqq f(c_2) \rightarrow$最小点$x^*$は$[c_1,r]$に含まれる。
証明
(1)$x^* \in [l,c_1]$のとき
$x^* \leqq c_1 \leqq c_2$なので、$c_1=\lambda x^*+(1-\lambda )c_2$となる$\lambda \in [0,1]$が存在する。
このとき、
\begin{align}
f(c_1) &= f(\lambda x^*+(1-\lambda)c_2) \\
& \leqq \lambda f(x^*)+(1-\lambda)f(c_2) \ (\because fは擬似凸関数)\\
& \leqq \lambda f(c_2)+(1-\lambda)f(c_2) \ (\because f(x^*) \leqq f(c_2))\\
& = f(c_2)
\end{align}
(2)$x^* \in [c_1,c_2]$のとき
$f(c_1) \leqq f(c_2)$と$f(c_1) \geqq f(c_2)$の少なくとも一方が成り立つ
(3)$x^* \in [c_2,r]$のとき
(1)と同様にすれば$f(c_1) \geqq f(c_2)$を得ることができる。
よって(1)~(3)より(✳︎)は示される。
$[Q.E.D.]$
三分探索の実装
三分探索の具体的な実装を以下に載せます(コード上のコメントアウトが実装で役に立つと思います。)。
①関数の定義域が実数上の閉区間である場合
以下では、ARC054-B ムーアの法則を考えます。この問題では考察により$f(x)=x+\frac{p}{2^{\frac{x}{1.5}}}$を最小にするような実数$x \in [0,10^{18}]$を考える問題に帰着できます。
ここで、この関数$f(x)$は二回微分が可能なので計算すると、$f^{''}(x)=(\log 2)^2(-\frac{2}{3})^2p \times 2^{-\frac{2x}{3}}>0$なので、関数$f(x)$は凸関数であることがわかります。3
よって、三分探索で最小点となる$x$を探索することができ、以下のようなコードを書くことができます。また、ここでは関数の定義域が整数ではなく実数であり誤差の範囲は$10^{-8}$まで許容されるので、一回の探索で探索範囲が$\frac{2}{3}$になることを考慮すれば、$\log_{\frac{3}{2}}\frac{10^{18}}{10^{-8}}=26\times \log_{\frac{3}{2}}{10}$回程度while文は回ることになり、十分に高速なプログラムとなります。
p=float(input())
# (1)最小にしたい関数fを定義する
def f(x):
global p
return x+p*pow(2,-(x/1.5))
# (2)関数fの最小値を探したい閉区間の両端をl,rと置く(l<=r)
l,r=0,10**18
# (3)誤差が10^-8を下回るまでwhile文を回す
while l+pow(10,-8)<r:
#(4)オーバーフローしないように以下のように三等分点を置く
c1=l+(r-l)/3
c2=r-(r-l)/3
#(5)更新を行う
if f(c1)<f(c2):
r=c2
else:
l=c1
# (6)最終的に出力するのはl,rのどちらでも良い
print(f(l))
②関数の定義域が整数上の閉区間である場合
以下では、ABC102D-Equal Cutを考えます。本解と少し異なる方法なので、自分の解説記事を参考記事として紹介します。
かなり難しい問題なので、実装方法のみ①の場合と比較して確認していただければと思います。
n=int(input())
a=list(map(int,input().split()))
s=[a[0]]
for i in range(1,n):
s.append(s[-1]+a[i])
# (1)最小にしたい関数fを定義する
def f(c,i):
global n,a,s
return abs(s[c]-(s[i]-s[c]))
# (1)
def g(c,i):
global n,a,s
return abs((s[c]-s[i])-(s[n-1]-s[c]))
ans=[]
for i in range(1,n-2):
ans_=[]
#(2)関数fの最小値を探したい閉区間の両端をl,rと置く(l<=r)
#ここではインデックスの値になる
l,r=0,i
#(3)整数なので、r=l,l+1,l+2のいずれかになれば良い
#逆にr>=l+3の場合はrとlの差をもっと小さくできる
while l+2<r:
#(4)三等分点(小数部分は切り捨て)
c1=l+(r-l)//3
c2=r-(r-l)//3
#(5)更新を行う
if f(c1,i)<f(c2,i):
r=c2
else:
l=c1
#(6)最終的に求めるのはl~rのうち関数fの値が最小になる要素
x=sorted([(f(j,i),j) for j in range(l,r+1)])[0][1]
ans_.append(s[x])
ans_.append(s[i]-s[x])
#右側決める
#(2)
l,r=i+1,n-1
#(3)
while l+2<r:
#(4)
c1=l+(r-l)//3
c2=r-(r-l)//3
#(5)
if g(c1,i)>g(c2,i):
l=c1
else:
r=c2
#(6)
x=sorted([(g(j,i),j) for j in range(l,r+1)])[0][1]
ans_.append(s[x]-s[i])
ans_.append(s[n-1]-s[x])
ans.append(max(ans_)-min(ans_))
print(min(ans))
最後に
三分探索を使った問題が解けずに悔しかったので数学的に厳密に考察をしました。
また、実装部分も自分なりに工夫したので参考にしてください。
そして、今回数学的に厳密な解説をするにあたり大学の同期に修正を手伝ってもらったので、ここに感謝の意を表します。
参考記事
二分探索アルゴリズムを一般化 〜 めぐる式二分探索法のススメ 〜
絶対にバグらない二分探索の実装パターンと、それがバグらない5つの理由