2025年11月時点における世界最高速の向聴数計算アルゴリズムを開発・実装してしまった件について

Last updated at 2025-11-08Posted at 2025-11-08

結論 - 2025年11月時点における世界最高速の向聴数計算アルゴリズムの実装

本稿で説明する向聴数計算アルゴリズムの実装は https://github.com/Cryolite/nyanten で公開しています．この実装による手牌1つあたりに対する向聴数計算の速度は， Intel Core i9-12900， Ubuntu 24.04.3 LTS， GCC 15.2.0 を利用して計測した結果，平均して約40ナノ秒でした．もしこの向聴数計算アルゴリズムの実装が2025年11月時点における世界最高速のものであることに異論がある場合は，より高速な実装を携えて筆者にまで連絡していただければ幸いです．

向聴数 - 本記事で提案するアルゴリズムが計算するものとは何か

向聴数とは，麻雀における手の進み具合を示す指標の1つで，「聴牌までに必要な自摸の最小回数」で定義されるものです．したがって，向聴数計算アルゴリズムとは，入力が2枚，5枚，8枚，11枚，14枚の麻雀牌の集まり（自摸直後の場合）もしくは1枚，4枚，7枚，10枚，13枚の麻雀牌の集まり（自摸直後以外の場合）であり，各々の入力を手牌と見立てて聴牌までに必要な自摸の最小回数を出力するものである，ということになります．

和了形は4面子1雀頭形（実際には副露を考慮するため $n$ 面子1雀頭形， $n \in \{ 0, 1, 2, 3, 4\}$），七対子形，国士無双形に大別されます．このうち，七対子形および国士無双形に対する向聴数の計算は容易なので本稿では説明しません．以下では，4面子1雀頭形に対する向聴数の計算にのみ焦点を絞って説明を展開します．

世間ではしばしば，4面子1雀頭形に対する向聴数の「定義」として

$\text{向聴数} = 8 - \text{面子の数} \times 2 - \text{面子候補の数}$

という計算式を挙げるものがあります．ただし，ここで

$\text{面子の数} = \text{順子の数}+\text{刻子の数}+\text{副露の数}$

$\text{面子候補の数} = \text{塔子の数} + \text{対子の数}$

です．この計算式は，「聴牌までに必要な自摸の最小回数」を近似計算するものとしてはかなり優秀で，特に人間が向聴数計算を行う際には極めて有用な計算式ではあるのですが，実際には「聴牌までに必要な自摸の最小回数」を正しく計算するものではありません．可能な $n$ 面子1雀頭形手牌のパタンは4250305029168216000通りありますが，このうち263674494通りの手牌に対してこの計算式は誤った数値を返します．¹²「向聴数計算アルゴリズム」として世間に広く出回っているものの中にはこの計算式（あるいはその亜種）に基づくものがあります³⁴が，それらは誤ったアルゴリズム（良く言って近似計算アルゴリズム）ということになります．さらに言えば，上記の計算式に基づく「向聴数計算アルゴリズム」は，数理的に正しく定義された向聴数に基づく向聴数計算アルゴリズム（例えば https://github.com/tomohxx/shanten-number や本稿で提案するもの）と比較して速度的にも何らの利点も見いだせるものではありません．したがって，上記の計算式に基づく「向聴数計算アルゴリズム」は現在においてはもはや特に採用するべき根拠の無いものであり，過去の遺物にすぎません．

上記の「向聴数の定義」が採用できないとすれば，向聴数とは一体何かということ（数理的に言えば，向聴数の定義とは何かということ）が問題になります．結論から言えば，与えられた手牌の向聴数とは，可能な全ての聴牌形を列挙した上で，その手牌から各々の聴牌形へと変形するために必要な自摸の最小回数を全て計算した際に，その中で最も小さい値のことになります．

しかしながら，この向聴数の定義には1つ問題があります．この向聴数の定義に基づくと，聴牌形と和了形のどちらも向聴数が0となり，聴牌形と和了形の区別がつかなくなります．そこで，聴牌形に対して0となり，和了形に対して-1となるような向聴数の定義の拡張を与えることにします．そのために「置換数」という数値を新たに導入することにします．ある手牌の置換数とは，可能な全ての和了形を列挙した上で，その手牌から各々の和了形へと変形するために必要な自摸の最小回数を全て計算した際に，その中で最も小さな値とします．この定義により，ある手牌が和了形の場合にはその手牌の置換数は0となり，ある手牌が聴牌形の場合にはその手牌の置換数は1となり，以下同様に，和了形でない場合は置換数は向聴数よりも1大きい値となります．

以下では，向聴数の代わりにこの置換数を計算することを主眼とします．

例えば，

という手牌の置換数（向聴数）を定義に従って計算するとどうなるかを考えます．まず，全ての可能な4面子1雀頭形和了形12859078207674通りを列挙します．これらの中から，上記の手牌から最小の自摸回数で至ることのできるものを探します．最終的に，そのような4面子1雀頭形和了形の1つとして，

が見つかります．上記の手牌からこの和了形へと変形するのに必要な自摸の最小回数は2なので，上記の手牌の置換数は2（向聴数は1）ということになります．

上記は入力された手牌の枚数が13枚または14枚の場合の置換数（向聴数）の計算手順となりますが，実際には副露を考慮する必要があります．そのため，入力された手牌が1枚または2枚の場合は，全ての0面子1雀頭の和了形を列挙した上でその中から変形に必要な自摸の回数が最小のものを探すことになります．以下同様に，入力された手牌が4枚または5枚の場合は，全ての1面子1雀頭の和了形を列挙した上でその中から変形に必要な自摸の回数が最小のものを探すことになります．入力された手牌が7枚または8枚の場合は，全ての2面子1雀頭の和了形を列挙した上でその中から変形に必要な自摸の回数が最小のものを探すことになります．入力された手牌が10枚または11枚の場合は，全ての3面子1雀頭の和了形を列挙した上でその中から変形に必要な自摸の回数が最小のものを探すことになります．

部分向聴数

上記において，例えば13枚または14枚の場合の置換数（向聴数）の計算手順では全ての可能な4面子1雀頭形和了形12859078207674通りを列挙すると説明しました．しかしながら，これはあくまで定義上の話であり，向聴数を計算するために，毎回，12859078207674通りの和了形を列挙していては計算がとても遅くなるのは自明でしょう．そこで，麻雀のルールを利用して向聴数をより高速に計算します．

手牌全体で4面子1雀頭を構成するには，例えば，萬子で1面子0雀頭を作り，筒子で0面子0雀頭を作り，索子で2面子1雀頭を作り，字牌で1面子0雀頭を作れば良いことになります．一般に，萬子で $m_0$ 面子 $h_0$ 雀頭を作り，筒子で $m_1$ 面子 $h_1$ 雀頭を作り，索子で $m_2$ 面子 $h_2$ 雀頭を作り，字牌で $m_3$ 面子 $h_3$ 雀頭を作るとした場合，手牌全体で4面子1雀頭を構成するには $m_0 + m_1 + m_2 + m_3 = 4$ かつ $h_0 + h_1 + h_2 + h_3 = 1$ を満たせばよいことになります．そのような組み合わせを全て列挙すると https://gist.github.com/Cryolite/29f64c49b198c17202ab74ff8a527ca7 となります．同様に，手牌全体で3面子1雀頭を構成するには $m_0 + m_1 + m_2 + m_3 = 3$ かつ $h_0 + h_1 + h_2 + h_3 = 1$ を満たせばよいことになります．そのような組み合わせを全て列挙すると https://gist.github.com/Cryolite/af18778dbe9dc5fbfbe25c83696caa8a となります．手牌全体で2面子1雀頭を構成するには $m_0 + m_1 + m_2 + m_3 = 2$ かつ $h_0 + h_1 + h_2 + h_3 = 1$ を満たせばよいことになります．そのような組み合わせを全て列挙すると https://gist.github.com/Cryolite/80a0204e0568983bd300ccc461b78246 となります．手牌全体で1面子1雀頭を構成するには $m_0 + m_1 + m_2 + m_3 = 1$ かつ $h_0 + h_1 + h_2 + h_3 = 1$ を満たせばよいことになります．そのような組み合わせを全て列挙すると https://gist.github.com/Cryolite/fa561f977d5197c8c824113136d721bc となります．手牌全体で0面子1雀頭を構成するには $m_0 + m_1 + m_2 + m_3 = 0$ かつ $h_0 + h_1 + h_2 + h_3 = 1$ を満たせばよいことになります．そのような組み合わせを全て列挙すると https://gist.github.com/Cryolite/3633cc5e8a26bef257dc0fd281bc8d10 となります．

以上の考察から，例えば，

という手牌の向聴数を計算する際には，

萬子で0面子0雀頭，筒子で0面子0雀頭，索子で0面子0雀頭，字牌で4面子1雀頭を作るのに必要な自摸の最小回数を計算する
萬子で0面子0雀頭，筒子で0面子0雀頭，索子で0面子1雀頭，字牌で4面子0雀頭を作るのに必要な自摸の最小回数を計算する
萬子で0面子0雀頭，筒子で0面子0雀頭，索子で1面子0雀頭，字牌で3面子1雀頭を作るのに必要な自摸の最小回数を計算する
……

という具合に， https://gist.github.com/Cryolite/29f64c49b198c17202ab74ff8a527ca7 に列挙した全ての場合に対する必要な自摸の最小回数を各々計算して，それらの中の最小の値が置換数ということになります．

以上の計算において必要な値は，まず手牌の萬子の部分だけに注目すると，

萬子の部分だけで0面子0雀頭を作るのに必要な自摸の最小回数
萬子の部分だけで1面子0雀頭を作るのに必要な自摸の最小回数
萬子の部分だけで2面子0雀頭を作るのに必要な自摸の最小回数
萬子の部分だけで3面子0雀頭を作るのに必要な自摸の最小回数
萬子の部分だけで4面子0雀頭を作るのに必要な自摸の最小回数
萬子の部分だけで0面子1雀頭を作るのに必要な自摸の最小回数
萬子の部分だけで1面子1雀頭を作るのに必要な自摸の最小回数
萬子の部分だけで2面子1雀頭を作るのに必要な自摸の最小回数
萬子の部分だけで3面子1雀頭を作るのに必要な自摸の最小回数
萬子の部分だけで4面子1雀頭を作るのに必要な自摸の最小回数

となり，以下，同様に，手牌の筒子の部分だけに注目して同様の値，手牌の索子の部分だけに注目して同様の値，手牌の字牌の部分だけに注目して同様の値，となります．

このように，ある手牌の置換数（向聴数）を計算するためには，その手牌の各色（萬子か筒子か索子か字牌か）の部分だけに注目して，その部分だけで $m$ 面子 $h$ 雀頭（$m \in \{ 0, 1, 2, 3, 4\},$ $h \in \{ 0, 1\}$）を作るのに必要な自摸の最小回数を計算すれば，後はそれらの値を組み合わせるだけでその手牌全体の置換数（向聴数）が計算できることになります．以下，ある手牌が与えられた時，その手牌のある色の部分だけに注目して，その部分だけで $m$ 面子 $h$ 雀頭（$m \in \{ 0, 1, 2, 3, 4\},$ $h \in \{ 0, 1\}$）を作るのに必要な自摸の最小回数のことを，（その色における $m$ 面子 $h$ 雀頭に対する）部分置換数と呼ぶことにします．

例えば，手牌

に対して，

萬子における $0$ 面子 $0$ 雀頭に対する部分置換数は $0$
萬子における $1$ 面子 $0$ 雀頭に対する部分置換数は $0$
萬子における $2$ 面子 $0$ 雀頭に対する部分置換数は $1$
萬子における $3$ 面子 $0$ 雀頭に対する部分置換数は $4$
萬子における $4$ 面子 $0$ 雀頭に対する部分置換数は $7$
萬子における $0$ 面子 $1$ 雀頭に対する部分置換数は $1$
萬子における $1$ 面子 $1$ 雀頭に対する部分置換数は $1$
萬子における $2$ 面子 $1$ 雀頭に対する部分置換数は $3$
萬子における $3$ 面子 $1$ 雀頭に対する部分置換数は $6$
萬子における $4$ 面子 $1$ 雀頭に対する部分置換数は $9$

となります．

また，ある手牌が与えられた時，その手牌の各色における部分置換数

$0$ 面子 $0$ 雀頭に対する部分置換数
$1$ 面子 $0$ 雀頭に対する部分置換数
$2$ 面子 $0$ 雀頭に対する部分置換数
$3$ 面子 $0$ 雀頭に対する部分置換数
$4$ 面子 $0$ 雀頭に対する部分置換数
$0$ 面子 $1$ 雀頭に対する部分置換数
$1$ 面子 $1$ 雀頭に対する部分置換数
$2$ 面子 $1$ 雀頭に対する部分置換数
$3$ 面子 $1$ 雀頭に対する部分置換数
$4$ 面子 $1$ 雀頭に対する部分置換数

を1列に並べたものを，その手牌の（その色における）部分置換数列と呼ぶことにします．

例えば，手牌

に対して，筒子における部分置換数列は $(0, 1, 2, 5, 8, 0, 1, 4, 7, 10)$ となります．

動的計画法による置換数（向聴数）の高速計算

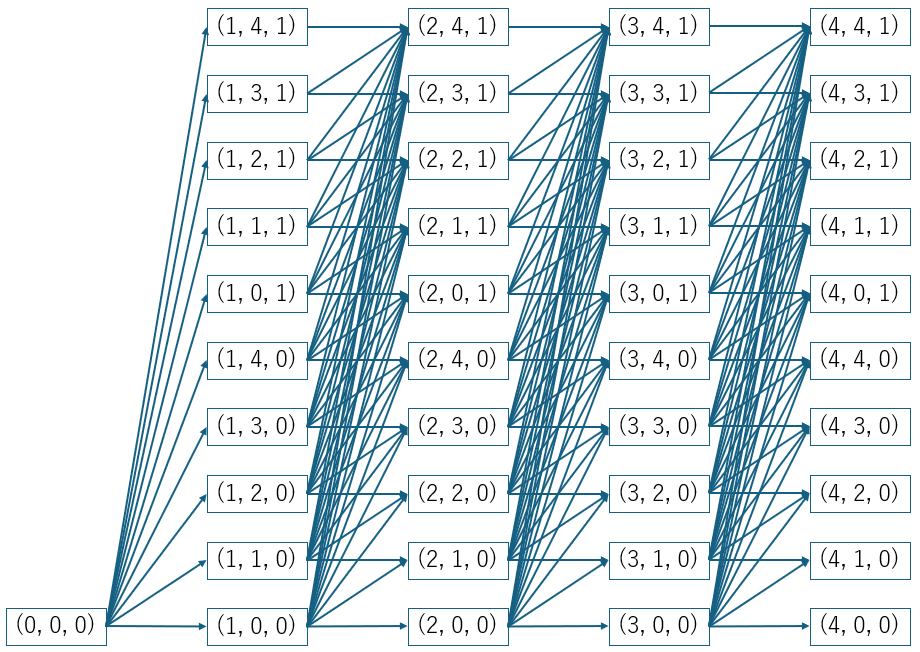
ある手牌が与えられた時，その手牌の各色の部分置換数列が計算されていれば，最終的な置換数（向聴数）は動的計画法により高速に計算できます．手牌全体の $m$ 面子1雀頭に対する置換数（向聴数）の計算において，この動的計画法は，以下のような有向非循環グラフにおけるノード $(0, 0, 0)$ からノード $(4, m, 1)$ へ至る最小コストのパスを探索する問題と等価になります．

ここで，

ノード $(0, 0, 0)$ からノード $(1, m, h)$ への辺のコストは萬子における $m$ 面子 $h$ 雀頭に対する部分置換数
ノード $(1, m, h)$ からノード $(2, m', h')$ への辺のコストは筒子における $m' - m$ 面子 $h' - h$ 雀頭に対する部分置換数
ノード $(2, m, h)$ からノード $(3, m', h')$ への辺のコストは索子における $m' - m$ 面子 $h' - h$ 雀頭に対する部分置換数
ノード $(3, m, h)$ からノード $(4, m', h')$ への辺のコストは字牌における $m' - m$ 面子 $h' - h$ 雀頭に対する部分置換数

となります．

最小完全ハッシュ関数による部分置換数列の事前計算

上記の説明の通り，ある手牌が与えられた時，その置換数（向聴数）を計算するためには，その手牌の

萬子における部分置換数列
筒子における部分置換数列
索子における部分置換数列
字牌における部分置換数列

を各々計算し，最後にこれらを動的計画法で組み合わせることが必要になります．ここで，ある手牌が与えられた時の各色の部分置換数列の計算が非常に遅いため，部分置換数列を事前に計算しておくというアイデアを採用することにします．つまり，数牌0枚から14枚までの集まり計405350通りの全てのパタンと，字牌0枚から14枚までの集まり計43130通りのパタンに対して，あらかじめ各々の部分置換数列を計算しておくことにします．

あらかじめ計算する部分置換数列は，数牌または字牌0枚から14枚までの集まりのパタンをキーとし，各々のキーに対応する部分置換数列を値とする何らかのデータ構造に格納します．ここで，どのようなデータ構造を採用するかが問題となります．本稿で紹介するものは，このデータ構造に最小完全ハッシュ関数を用いた配列を採用します．

まずキーですが，数牌の場合は $0, 1, 2, 3, 4$ のいずれかの数字の9つの並びであって数字の合計が14を超えないもので，字牌の場合は $0, 1, 2, 3, 4$ のいずれかの数字の7つの並びであって数字の合計が14を超えないもので，各々表現できるのは自明でしょう．

このようなキーに対して，単純には

特に工夫の無いハッシュ関数を用いたハッシュテーブル
キーを5進数による自然数の表現と見なして配列の添え字のインデックスを計算するもの

の2つが部分置換数列を格納するデータ構造として考えられます．しかしながら，前者はハッシュ関数の速度が律速となる上に，ハッシュが衝突するためにキーをハッシュテーブルに記録しておく必要があります．後者は数字の合計が14を超えないという制約を無視するために配列のサイズが必要以上に大きくなります．

本稿で紹介するアイデアは， $0, 1, 2, 3, 4$ のいずれかの数字の並びであって数字の合計が14を超えないものに対して，0から順に辞書順で番号を付与するものです．言い換えれば， $0, 1, 2, 3, 4$ のいずれかの数字の並びであって数字の合計が14を超えないものに対する最小完全ハッシュ関数を採用します．

この最小完全ハッシュ関数の詳しい説明は

を参照してください．

結果として，部分置換数列を格納するデータ構造として本稿で採用するものは，数牌に対してサイズが405350の配列となり，字牌に対してサイズが43130の配列となります．

部分置換数列の差分圧縮

（本節のアイデアの基本的な部分はtomohxx氏によって発見されたものです．）

あらかじめ計算する部分置換数列ですが，単純には $0$ から $9$ までのいずれかの自然数を10個並べたものになります（最大が $9$ なのは $4$ 面子 $1$ 雀頭形に対する置換数の最大が $9$ （向聴数の最大が $8$）であることによります）が，符号化を工夫することにより実際のサイズを圧縮することができます．

まず， $0$ 面子 $0$ 雀頭に対する部分置換数は常に $0$ であるため記録しなくて済みます．さらに，部分置換数列そのものを記録する代わりに以下の数値を記録することにします：

$1 \text{面子} 0 \text{雀頭に対する部分置換数}$
$(2 \text{面子} 0 \text{雀頭に対する部分置換数}) - (1 \text{面子} 0 \text{雀頭に対する部分置換数})$
$(3 \text{面子} 0 \text{雀頭に対する部分置換数}) - (2 \text{面子} 0 \text{雀頭に対する部分置換数})$
$(4 \text{面子} 0 \text{雀頭に対する部分置換数}) - (3 \text{面子} 0 \text{雀頭に対する部分置換数})$
$0 \text{面子} 1 \text{雀頭に対する部分置換数}$
$(1 \text{面子} 1 \text{雀頭に対する部分置換数}) - (1 \text{面子} 0 \text{雀頭に対する部分置換数})$
$(2 \text{面子} 1 \text{雀頭に対する部分置換数}) - (2 \text{面子} 0 \text{雀頭に対する部分置換数})$
$(3 \text{面子} 1 \text{雀頭に対する部分置換数}) - (3 \text{面子} 0 \text{雀頭に対する部分置換数})$
$(4 \text{面子} 1 \text{雀頭に対する部分置換数}) - (4 \text{面子} 0 \text{雀頭に対する部分置換数})$

1.，2.，3.，4.は理論上 $3$ を超える数値となることはありません．また，5.，6.，7.，8.，9.は理論上 $2$ を超える数値となることはありません．したがって，上記8つの数値は $\log_2(4^4 \times 3^5) = \log_2 62208 = 15.924...$ ビットにエンコードすることができ，16ビット整数に格納することができます．もちろん，1.から9.までの数値を用いて，元の部分置換数列を完全に復号することが可能です．

部分置換数列をこのアイデアで圧縮したものを，以下，部分置換数列の差分圧縮符号と呼ぶことにします．

動的計画法の事前計算

以上により，ある手牌が与えられた時，その置換数（向聴数）を計算する手順は

その手牌の萬子の部分の最小完全ハッシュを計算
1.で計算したハッシュを添え字として配列から（萬子における）部分置換数列を参照
その手牌の筒子の部分の最小完全ハッシュを計算
3.で計算したハッシュを添え字として配列から（筒子における）部分置換数列を参照
その手牌の索子の部分の最小完全ハッシュを計算
5.で計算したハッシュを添え字として配列から（索子における）部分置換数列を参照
その手牌の字牌の部分の最小完全ハッシュを計算
7.で計算したハッシュを添え字として配列から（字牌における）部分置換数列を参照
2.，4.，6.，8.で参照した部分置換数列を動的計画法で組み合わせて最終的な置換数（向聴数）を算出

となります．ここで，9.における動的計画法が全体の計算速度の律速部分となるため，この部分をさらに高速化します．

数牌0枚から14枚までの組み合わせは405350通りありますが，数牌が取りうる部分置換数列のパタンは全部で126通りしかないことが分かっています．また，字牌0枚から14枚までの組み合わせは43130通りありますが，字牌が取りうる部分置換数列のパタンは全部で55通りしかないことが分かっています⁵．そこで，この数少ない部分置換数列のパタンの組み合わせによる動的計画法をあらかじめ計算しておくというアイデアに思い至ります．

まず，数牌が取りうる部分置換数列のパタンに $0$ から $125$ までの番号を付与します．この番号を部分置換数列番号と呼ぶことにします．同様に，字牌が取りうる部分置換数列のパタンにも $0$ から $54$ までの部分置換数列番号を付与します．

次に，数牌が取りうる部分置換数列のパタン126通りと同じく数牌が取りうる部分置換数列のパタン126通りとを組み合わせてできる全ての可能な部分置換数列のパタン（合わせて180通りしかありません）を列挙し，各々に $0$ から $179$ までの番号を付与します．この番号を第一複合部分置換数列番号と呼ぶことにします．また，この組み合わせを $126 \times 126$ の2次元配列にあらかじめ記録しておきます．

さらに，第一複合部分置換数列のパタン180通りと数牌が取りうる部分置換数列のパタン126通りとを組み合わせてできる全ての可能な部分置換数列のパタン（合わせて180通りしかありません）を列挙し，各々に $0$ から $179$ までの番号を付与します．この番号を第二複合部分置換数列番号と呼ぶことにします．また，この組み合わせを $180 \times 126$ の2次元配列にあらかじめ記録しておきます．

最後に，第二複合部分置換数列のパタン180通りと字牌が取りうる部分置換数列のパタン55通りとを組み合わせてできる全ての可能な部分置換数列のパタン（合わせて180通りしかありません）を列挙し， $180 \times 55$ の2次元配列に対応する部分置換数列をあらかじめ記録しておきます．

以上により，ある手牌が与えられた時，その置換数（向聴数）を計算する手順は

その手牌の萬子の部分の最小完全ハッシュを計算
1.で計算したハッシュを添え字として配列から萬子における部分置換数列番号を参照
その手牌の筒子の部分の最小完全ハッシュを計算
3.で計算したハッシュを添え字として配列から筒子における部分置換数列番号を参照
2.と4.で参照した部分置換数列番号を2次元配列の添え字として第一複合部分置換数列番号を参照
その手牌の索子の部分の最小完全ハッシュを計算
6.で計算したハッシュを添え字として配列から索子における部分置換数列番号を参照
5.で参照した第一複合部分置換数列番号と7.で参照した部分置換数列番号を2次元配列の添え字として第二複合部分置換数列番号を参照
その手牌の字牌の部分の最小完全ハッシュを計算
9.で計算したハッシュを添え字として配列から字牌における部分置換数列番号を参照
8.で参照した第二複合部分置換数列番号と10.で参照した部分置換数列番号を2次元配列の添え字として置換数を参照

となります．

https://zenn.dev/tomohxx/articles/aecace4e3a3bc1 ↩
https://github.com/tomohxx/shanten-validation ↩
https://mahjong.ara.black/etc/shanten/index.htm ↩
https://www.amazon.co.jp/dp/4798067881 ↩
数牌や字牌が取りうる部分置換数列のパタンの数が極めて少ないという偉大な発見はtomohxx氏によってなされました．　 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up