【PyTorch Geometric】Node2Vecを用いたNodeの特徴量の抽出

前提の確認

Node2Vecの概要

Node2VecはWord2Vecに用いられるSkip-gram architectureを用いてノードの特徴量抽出を行う手法です。以下、Node2Vecにおける学習の大まかな仕組みについて論文の数式を元に確認します。

まず、グラフ$G=(V,E)$のノード$u \in V$の特徴量抽出を行う関数を$f(u) \in \mathbb{R}^{d}$とおくとき、ノード$n_{i} \in V$が$u$の近傍である確率$P(n_{i}|f(u))$を下記のような式で定義します。

P(n_{i}|f(u)) = \frac{\exp{(f(n_i) \cdot f(u))}}{\sum_{v \in V} \exp{(f(v) \cdot f(u))}}

$n_{i} \in V$であるので、上記はSoftmax関数の式であると解釈できます。次に$N_{S}(u) \subset V$を近傍サンプリング戦略(neighborhood sampling strategy)$S$によって選ばれたノード$u$の近傍ノードの集合であると定義します。このとき、$u$の近傍に$n_i$が選ばれる確率は他のノードが$u$の近傍に選ばれる確率に関与しない(Conditional independence)ので、下記のように$P(N_{S}(u)|f(u))$(集合$N_{S}(u)$がノード$u$の近傍である確率)を表すことができます。

P(N_{S}(u)|f(u)) = \prod_{n_i \in N_{S}(u)} P(n_{i}|f(u))

Node2Vecの目的関数(log-likelihood function)を$L(\theta)$($\theta$は$f$のパラメータ)とおくと、上記の$P(N_{S}(u)|f(u))$を元に$L(\theta)$は下記のように表すことができます。

\begin{align}
L(\theta) &= \sum_{v \in V} \log{P(N_{S}(u)|f(u))} \\
  &= \sum_{v \in V} \log{ \left[ \prod_{n_i \in N_{S}(u)} P(n_{i}|f(u)) \right] } \\
  &= \sum_{v \in V} \sum_{n_i \in N_{S}(u)} \log{P(n_{i}|f(u))} \\
  &= \sum_{v \in V} \sum_{n_i \in N_{S}(u)} \log{ \frac{\exp{(f(n_i) \cdot f(u))}}{\sum_{v \in V} \exp{(f(v) \cdot f(u))}} } \\
  &= \sum_{v \in V} \sum_{n_i \in N_{S}(u)} \log{ \frac{\exp{(f(n_i) \cdot f(u))}}{ Z_{u} }} \\
  &= \sum_{v \in V} \sum_{n_i \in N_{S}(u)} \left[ -\log{Z_u} + f(n_i) \cdot f(u) \right] \\
Z_{u} &= \sum_{v \in V} \exp{(f(v) \cdot f(u))}
\end{align}

Node2Vecの学習にあたっては上記の$L(\theta)$の最大化によって$\theta$の最適化を行います。

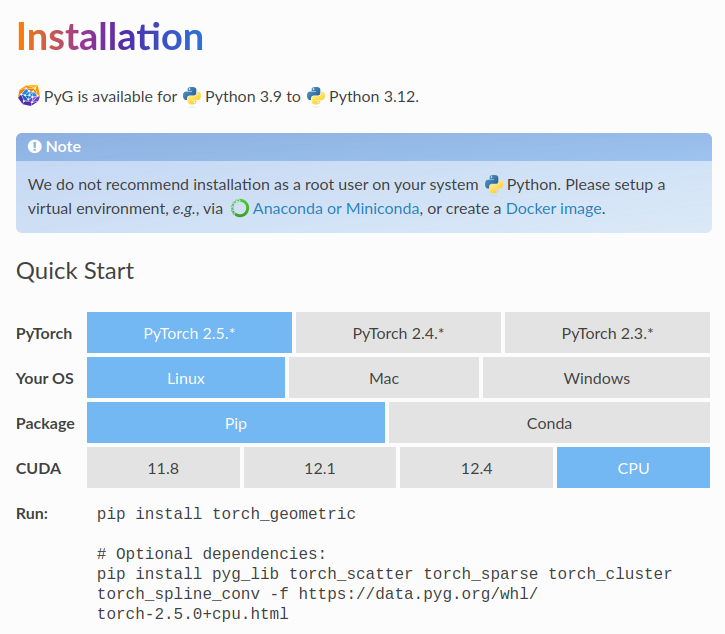
PyTorch Geometricのインストール

PyTorch Geometricドキュメント

PyTorch Geometricのインストールにあたっては上記に基づいて行えば良いです。OSやCUDAのバージョンなどによってコマンドが変わるので、注意して確認した上でインストールを行うと良いと思います。

Coraデータセットの入手と確認

当記事では上記に基づいてNode2Vecの実装の確認を行うにあたって、PlanetoidからCoraデータセットを用います。Coraデータセットは下記を実行することで入手と表示が可能です。

from torch_geometric.datasets import Planetoid


dataset = Planetoid('./data/Planetoid', name='Cora')
data = dataset[0]

print(len(dataset))
print(data)
print(data.is_directed)

・実行結果

1
Data(x=[2708, 1433], edge_index=[2, 10556], y=[2708], train_mask=[2708], val_mask=[2708], test_mask=[2708])
False

上記より、Coraデータセットはノードが2708個、エッジが10556本の無向グラフ(undirected graph)であることが確認できます。

Node2Vecの学習

Node2Vecの学習

下記のようなコードを動かすことでNode2Vecの学習を行うことができます。

import torch
from torch_geometric.nn import Node2Vec
from torch_geometric.datasets import Planetoid

data = Planetoid('./data/Planetoid', name='Cora')[0]

device = 'cuda' if torch.cuda.is_available() else 'cpu'

model = Node2Vec(
    data.edge_index,
    embedding_dim=100,
    walks_per_node=10,
    walk_length=20,
    context_size=10,
    p=1.0,
    q=1.0,
    num_negative_samples=1,
).to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

loader = model.loader(batch_size=128, shuffle=True, num_workers=4)
pos_rw, neg_rw = next(iter(loader))

def train():
    model.train()
    total_loss = 0
    for pos_rw, neg_rw in loader:
        optimizer.zero_grad()
        loss = model.loss(pos_rw.to(device), neg_rw.to(device))
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    return total_loss / len(loader)
    
    
z1 = model()  # Full node-level embeddings.
z2 = model(torch.tensor([0, 1, 2]))  # Embeddings of first three nodes.

print(model)
print(z1.shape)
print(z2.shape)

・実行結果

Node2Vec(2708, 100)
torch.Size([2708, 100])
torch.Size([3, 100])

実行結果より、modelの学習結果を用いることで、それぞれのノードの100次元の特徴量が抽出できていることが確認できます。

Node2Vecのmodel

Node2Vecのmodelの実装は上記より確認できます。

class Node2Vec(torch.nn.Module):
    (中略)
    def __init__(
        self,
        edge_index: Tensor,
        embedding_dim: int,
        walk_length: int,
        context_size: int,
        walks_per_node: int = 1,
        p: float = 1.0,
        q: float = 1.0,
        num_negative_samples: int = 1,
        num_nodes: Optional[int] = None,
        sparse: bool = False,
    ):
        super().__init__()

        if WITH_PYG_LIB and p == 1.0 and q == 1.0:
            self.random_walk_fn = torch.ops.pyg.random_walk
        elif WITH_TORCH_CLUSTER:
            self.random_walk_fn = torch.ops.torch_cluster.random_walk
        else:
            if p == 1.0 and q == 1.0:
                raise ImportError(f"'{self.__class__.__name__}' "
                                  f"requires either the 'pyg-lib' or "
                                  f"'torch-cluster' package")
            else:
                raise ImportError(f"'{self.__class__.__name__}' "
                                  f"requires the 'torch-cluster' package")

        self.num_nodes = maybe_num_nodes(edge_index, num_nodes)

        row, col = sort_edge_index(edge_index, num_nodes=self.num_nodes).cpu()
        self.rowptr, self.col = index2ptr(row, self.num_nodes), col

        self.EPS = 1e-15
        assert walk_length >= context_size

        self.embedding_dim = embedding_dim
        self.walk_length = walk_length - 1
        self.context_size = context_size
        self.walks_per_node = walks_per_node
        self.p = p
        self.q = q
        self.num_negative_samples = num_negative_samples

        self.embedding = Embedding(self.num_nodes, embedding_dim,
                                   sparse=sparse)

        self.reset_parameters()
    (中略)
    def forward(self, batch: Optional[Tensor] = None) -> Tensor:
        """Returns the embeddings for the nodes in :obj:`batch`."""
        emb = self.embedding.weight
        return emb if batch is None else emb[batch]

上記より、Node2Vecのmodelではbatchを入力した際はbatchのembeddingを、入力しない際は全てのノードのembeddingを返していることが確認できます。