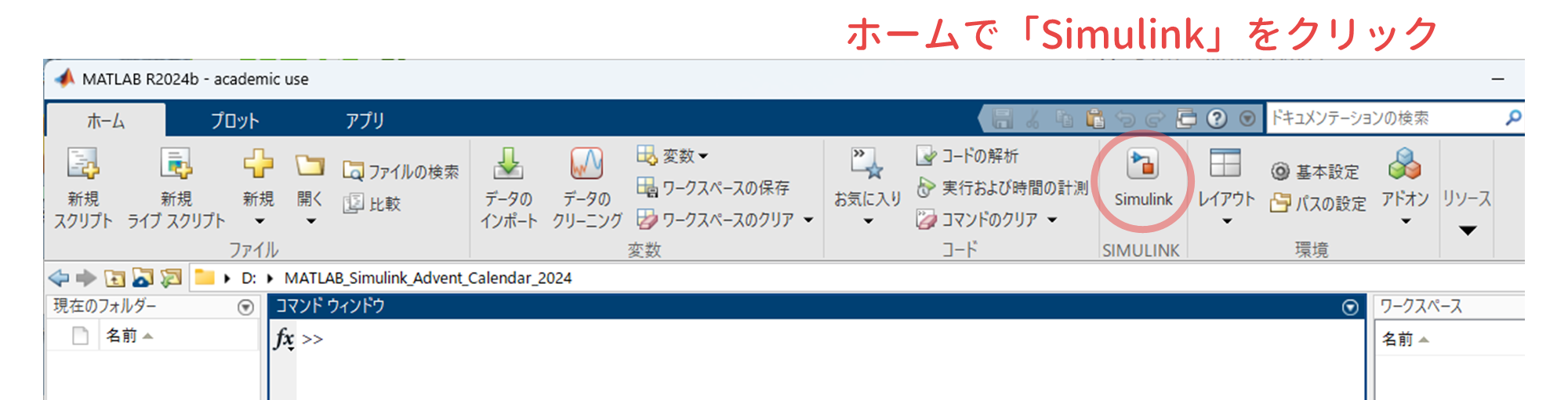
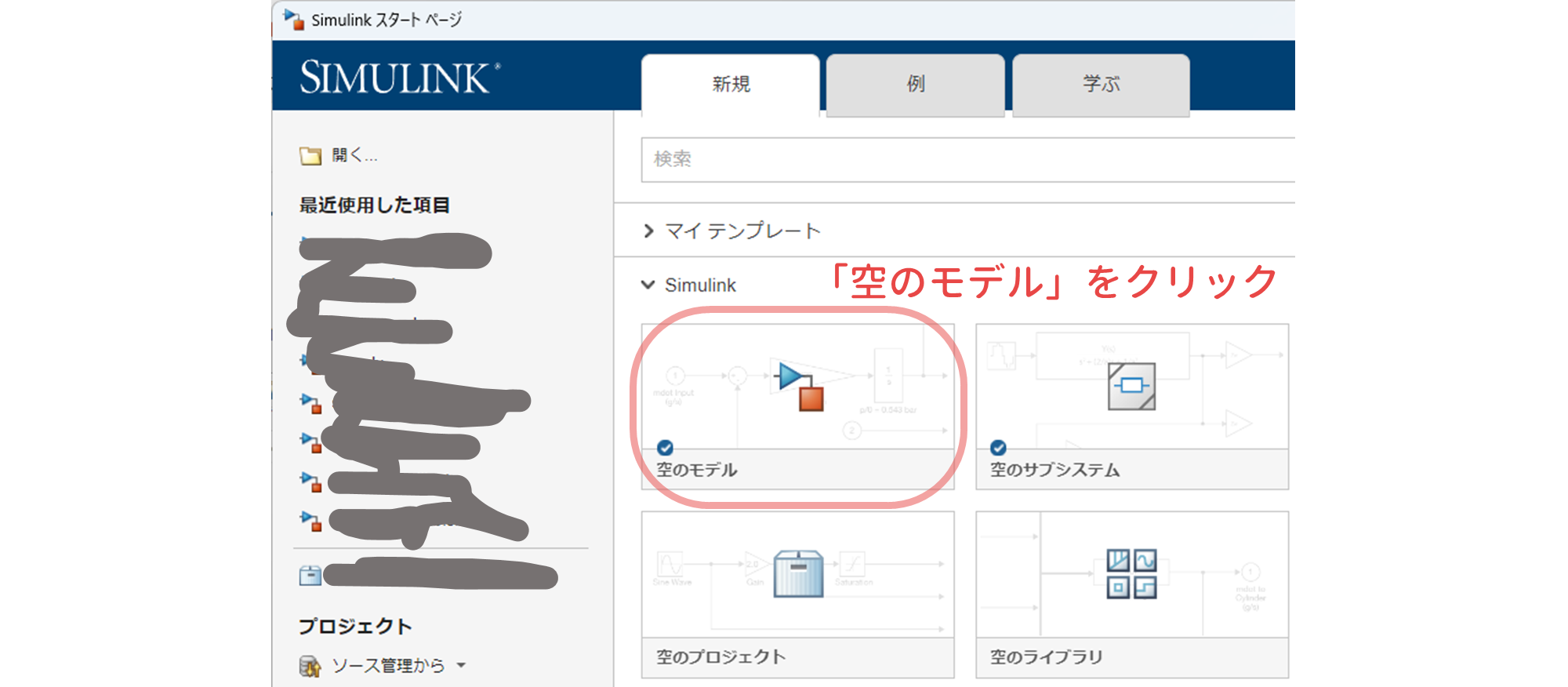
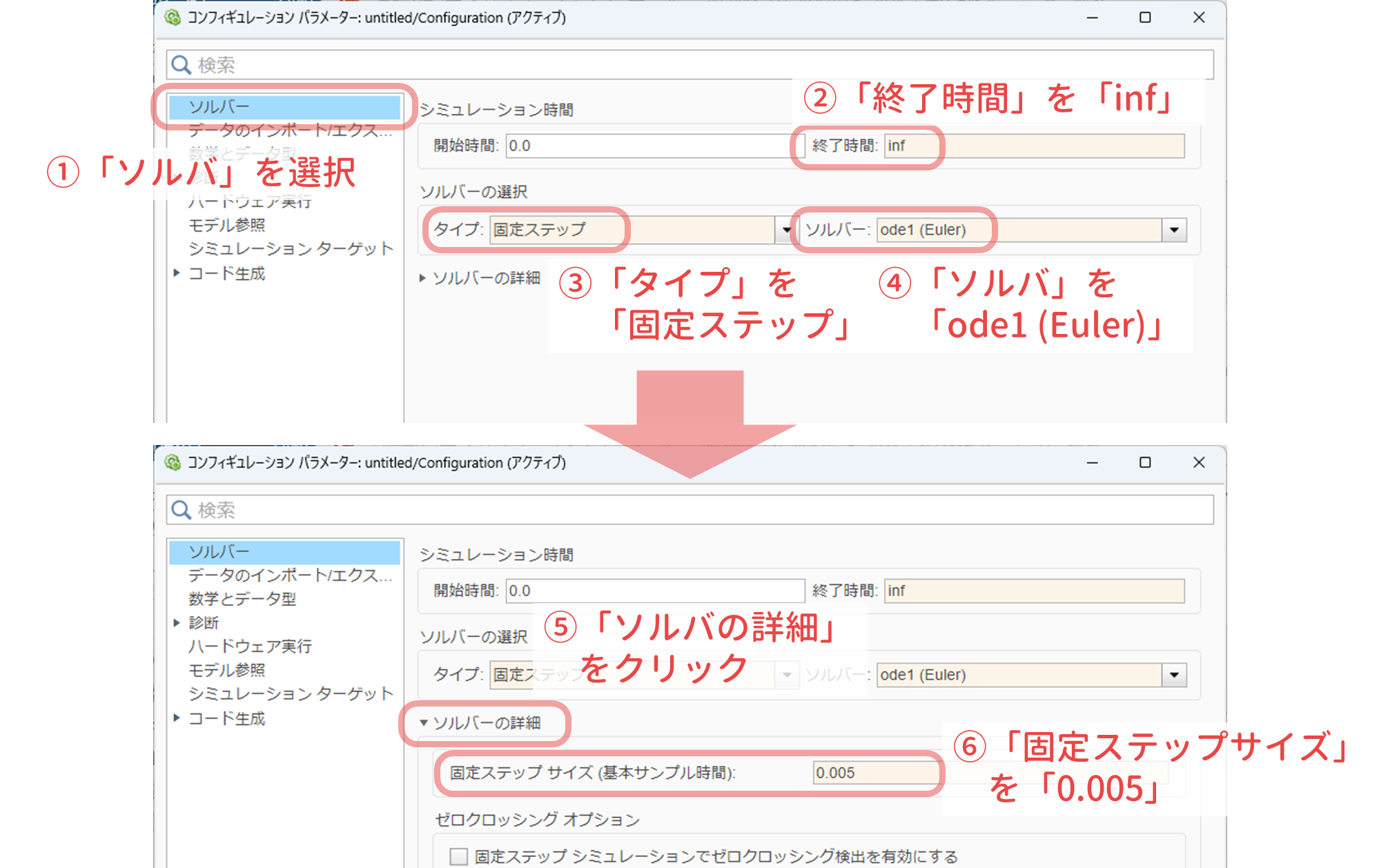
MATLAB 芸や Simulink 芸を披露する年末恒例のアドカレ MATLAB/Simulink Advent Calendar 2024 に今年も参加してみました．制御工学の界隈だと年末年始は MSCS（SICE 制御部門マルチシンポジウム） の原稿締切に追われるはずなのですが，なんとアドカレの記事を優先するという暴挙！ （イヤぁ…… きっと来年度の授業か何かに使うはずだし……）
1. はじめに
2023 年のアドカレの記事
では，Simulink Support Package for Arduino Hardware（以下，Simulink Support Package と略記）を利用して Arduino Mega 2560 R3（以下，Arduino Mega と略記）により
- DC モータの駆動
- ロータリエンコーダからの角度検出
を行う方法について説明しました．
今年のアドカレの記事では，6 軸センサの使用方法について説明します．そして，最終的には，車輪型倒立振子の倒立を目指します！
元ネタは卒研生が製作したこちらです．
これを，汎用で使いやすいように部品構成を見直しました．
2. ソフトウェア環境
必要なソフトウェアは
- MATLAB
- Simulink
- Control System Toolbox
および無償で提供されている
- Simulink Support Package for Arduino Hardware
です．
Simulink Support Package for Arduino Hardware のインストール手順については，たとえば，Qiita の記事
の 3 章を参照してください．
3. 6 軸センサの使用方法
3.1 6 軸センサってなんなのさ
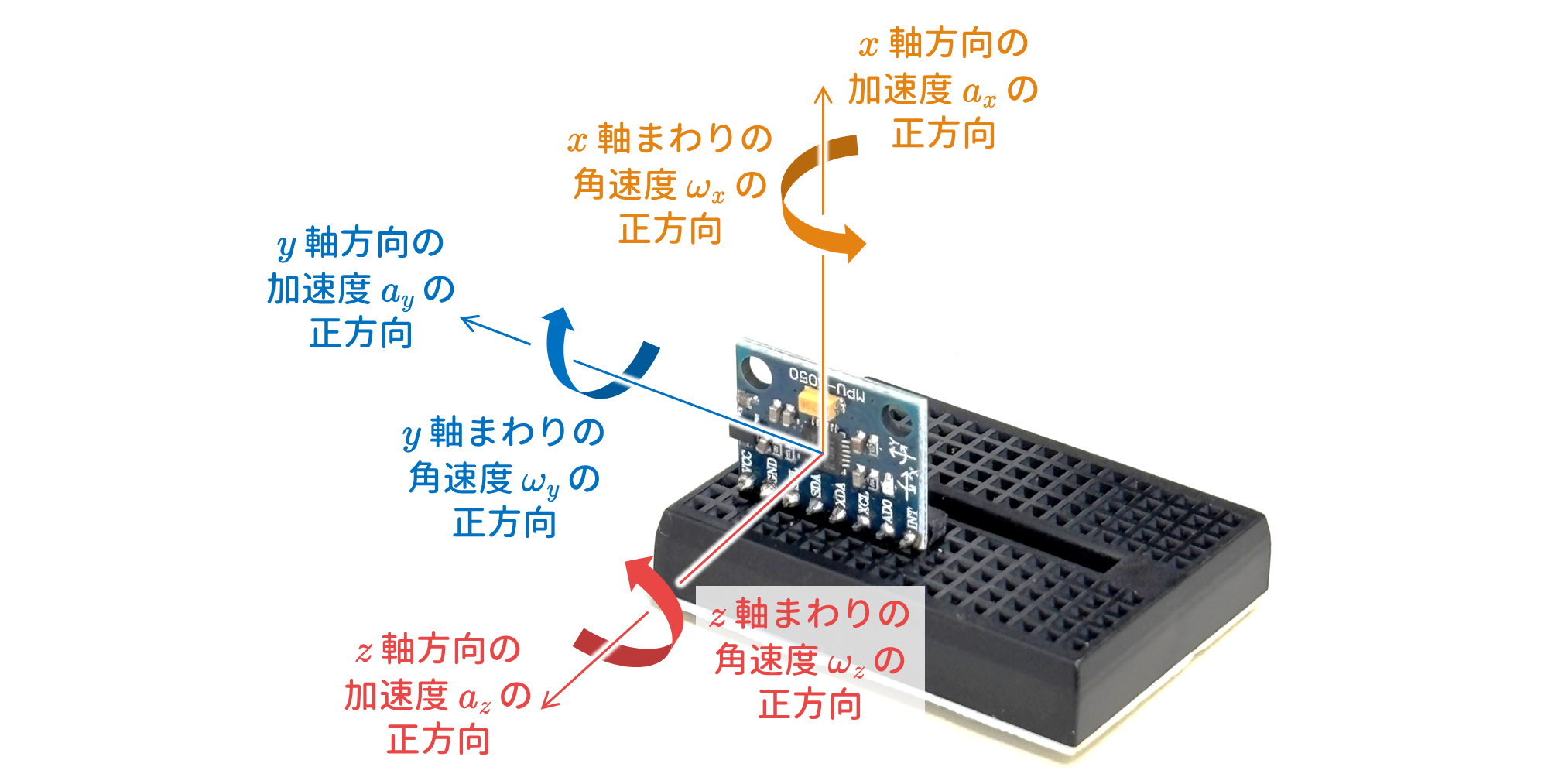
6 軸センサとは，
- $x$, $y$, $z$ 軸まわりの角速度 $\omega_x$, $\omega_y$, $\omega_z$
- $x$, $y$, $z$ 軸方向の加速度 $a_x$, $a_y$, $a_z$
を検出するセンサであり，ジャイロセンサ（角速度センサ）と加速度センサを組み合わせたものです．
そして，後述しますが，6 軸センサによりセンシングされた角速度 $\omega_x$, $\omega_y$, $\omega_z$ と加速度 $a_x$, $a_y$, $a_z$ を利用すると，$\pmb{x}$, $\pmb{y}$, $\pmb{z}$ 軸まわりの角度 $\pmb{\theta_x}$, $\pmb{\theta_y}$, $\pmb{\theta_z}$ を算出することができるんです！
ちなみに，ジャイロセンサ（角速度センサ）と加速度センサに加えて，
- $x$, $y$, $z$ 軸方向の地磁気
を検出するコンパス（方位）センサを組み合わせたものを 9 軸センサといいます．また，6 軸センサや 9 軸センサは IMU センサ（慣性センサ）と呼ばれることもあります．
IMU は Inertial Measurement Unit（慣性測定ユニット）の略です．
3.2 電子部品リスト (2024/12/06)
| 型番 | メーカー | 購入先 | 価格 | |
|---|---|---|---|---|
| マイコンボード | Arduino Mega 2560 R3 | Arduino | RS | 5,940 円 |
| 6 軸センサ （はんだ付けオプション：L 字ピン） |
MPU6050 (GY-521) | - | 電子工作ステーション | 360 円 （+500 円） |
| ミニブレッドボード | BB-601 (Black) | 慈渓市万捷電子有限公司 | 秋月電子通商 | 160 円 |
| USB ケーブル（リールケーブル A-B タイプ） | - | COMON(カモン) | amazon | 584 円 |
(a) 6 軸センサ MPU6050
今回の主役は電子工作ステーションさんで購入した 6 軸センサ MPU6050
です．コレって 360 円なので，かなりお安いです！ なお，本製品はモジュールとピンがはんだ付けされていない状態で販売されていますが， 電子工作ステーションさんに 500 円の追加料金を払えば，「Pin はんだ付けサービス」によりはんだ付けされた状態で購入できます．
付属するピンは「ストレートタイプ」と「L 字タイプ」の 2 種類がありますが，「L 字タイプ」としました．ブレッドボードに挿し込むと，以下のようになります．
(b) Arduino Mega 2560 R3
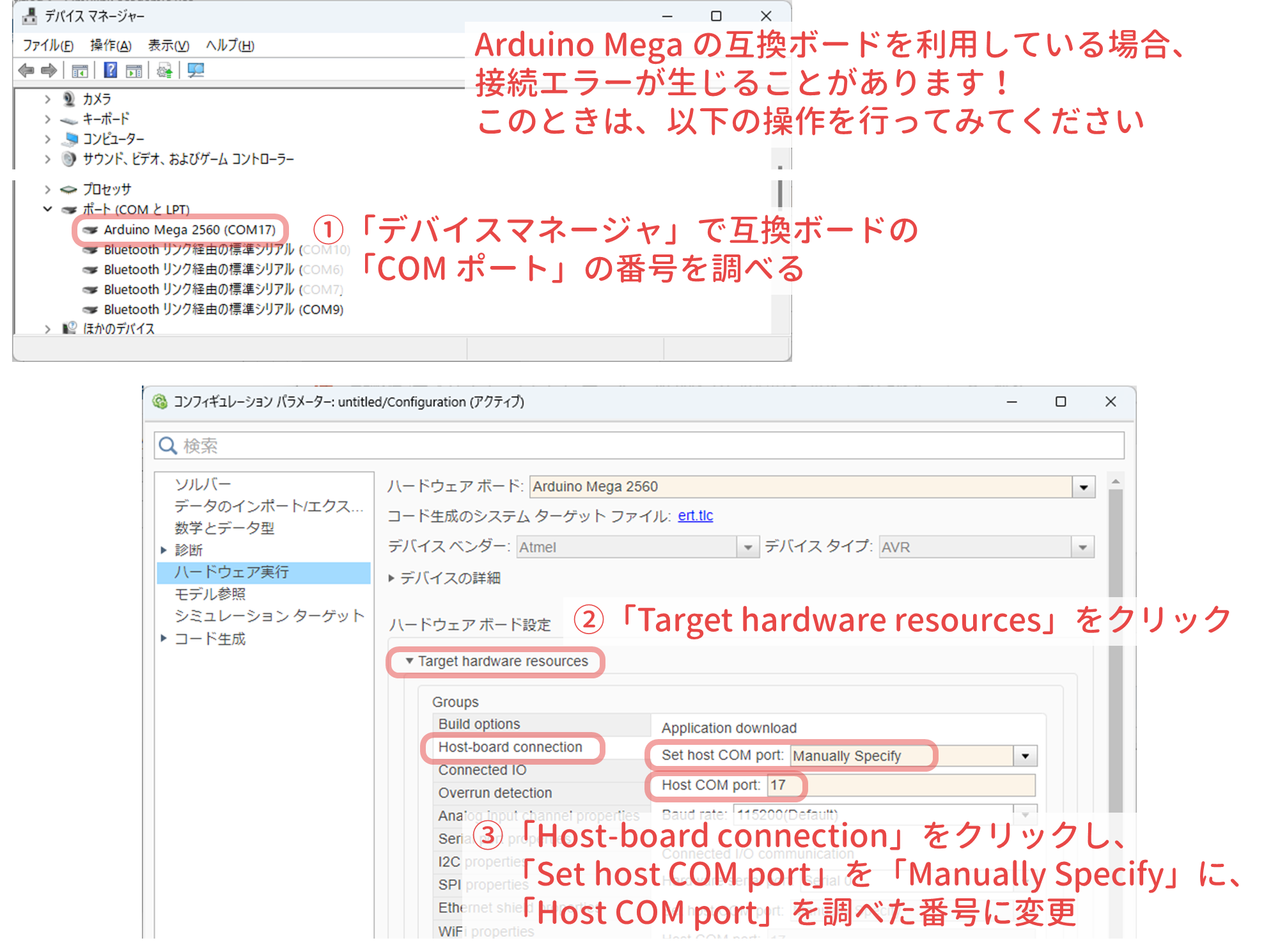
今回は，純正の Arduino Mega 2560 R3 を利用しました．互換品でも動作することが多いですが，手動で COM ポート番号を指定する必要があったりして面倒なので，純正を利用しています．
また，6 軸センサの動作を確認するだけであれば，Arduino Uno R3 を利用しても大丈夫ですが，Arduino Mega と比べて接続できる DC モータやエンコーダの数が少ないです．なお，Simulink Support Package は R2024b から Arduino Uno R4 WiFi にも対応しています（私はまだ使用したことがないですが…）．
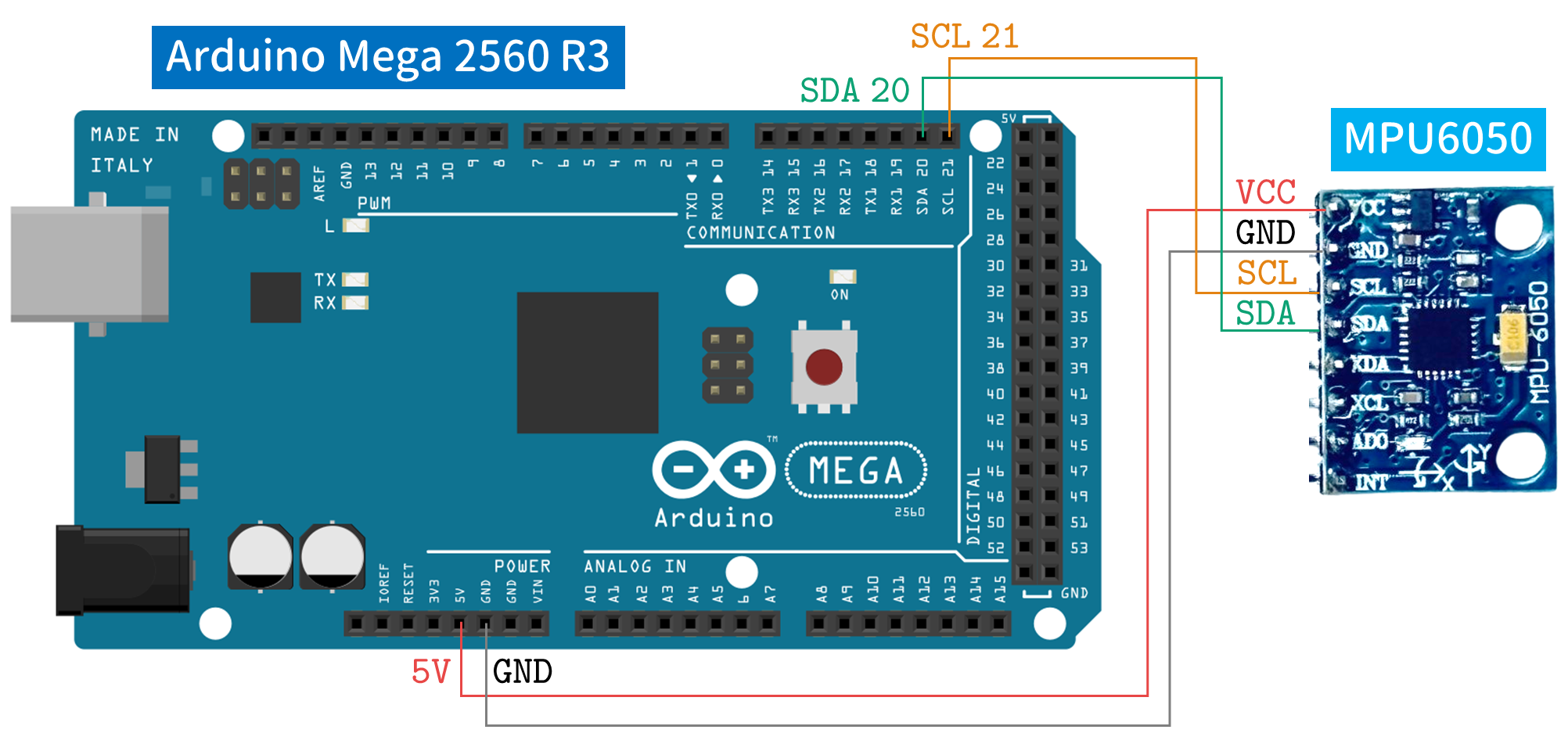
3.3 Arduino Mega と MPU6050 との接続
6 軸センサ MPU6050 は I²C（アイ・スクエア・シー，Inter-Integrated Circuit）接続で使用されます．各ピンの機能は以下のとおりです．
各ピンの機能
- ${\tt VCC}$：電源入力ピンです．通常，3.3 V または 5 V で動作します．
- ${\tt GND}$：システムの共通グラウンドに接続します．
- ${\tt SCL (Serial\ Clock\ Line)}$：I²C 通信のクロック信号を提供します．マスター（マイコンなど）からのクロック信号を受け取ります．
- ${\tt SDA (Serial\ Data\ Line)}$：I²C 通信のデータラインです．マスターとスレーブ間でデータを送受信します．
- ${\tt XDA (External\ Data\ Line)}$：拡張用の I²C データラインです．他の I²C デバイスをチェーン接続する場合（他の I²C デバイスを増設する場合）に使用されます．
-
${\tt XCL (External\ Clock\ Line)}$：拡張用の I²C クロックラインです．他の I²C デバイスをチェーン接続する場合に使用されます．
他の I²C デバイスをチェーン接続する場合に使用されます。 - ${\tt AD0 (Address\ Select)}$：I²C アドレス選択ピンです。このピンを GND に接続すると I²C アドレスは 0x68，VCC に接続すると 0x69 になります．複数の MPU6050 を1つの I²C バスに接続する場合，このピンでアドレスを切り替えます．
- ${\tt INT (Interrupt)}$：割り込み信号を出力するピンです．
これらのなかで今回使用するピンは
- ${\tt VCC}$
- ${\tt GND}$
- ${\tt SCL}$
- ${\tt SDA}$
の４つであり，MPU6050 と Arduino Mega を下図のように接続します．
具体的には，下図のように，MPU6050 をブレッドボードとジャンパ線で Arduino Mega と接続するとよいでしょう．なお，下図では，ジャンパ線のピン付近をテープで巻いています．
3.4 Simulink ブロック
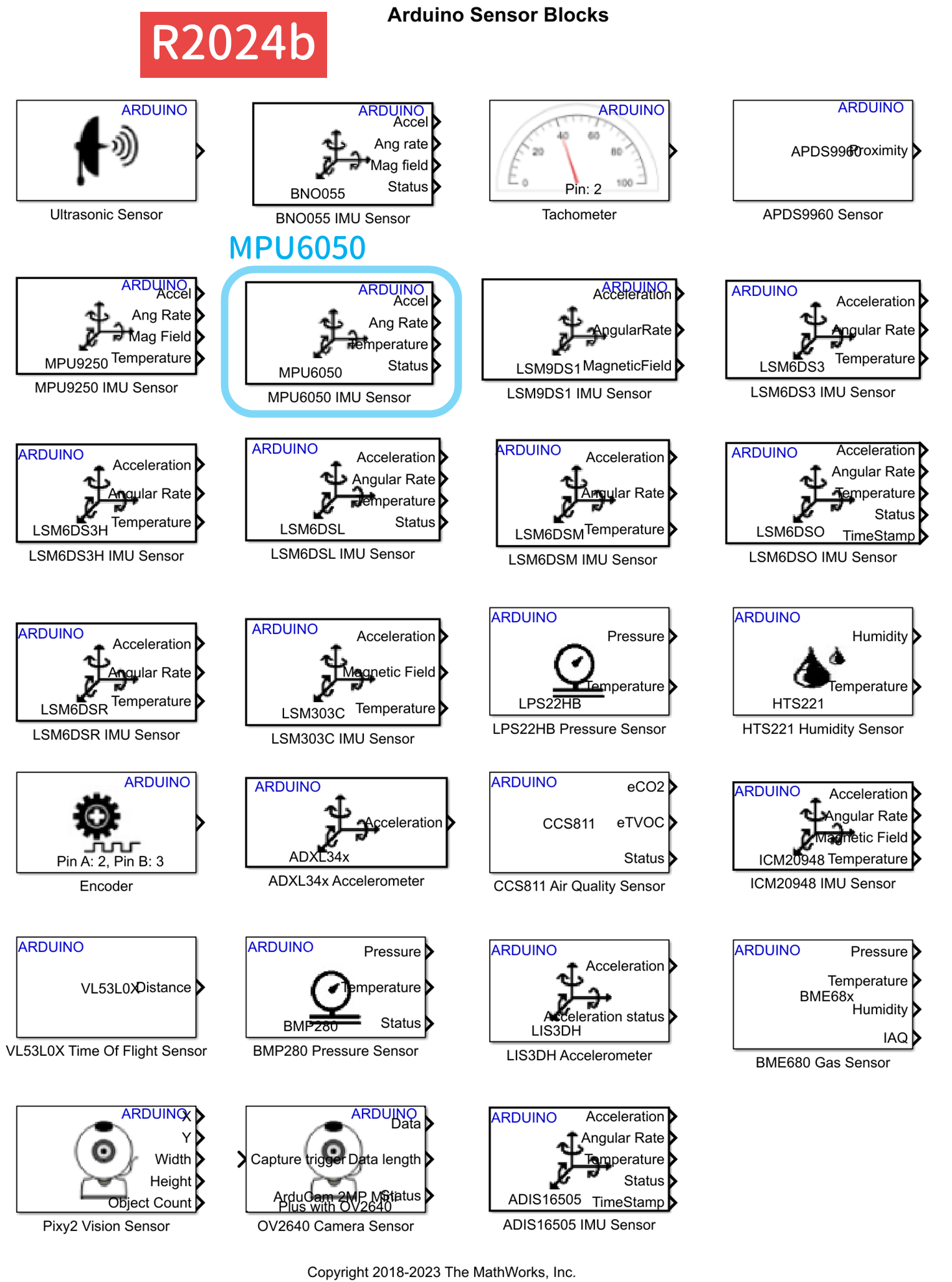
3.4.1 ライブラリ
Simulink Support Package はいくつかの IMU センサに対応しています．執筆時点の最新バージョン R2024b では，Simulink のライブラリブラウザの
- Simulink Support Package for Arduino Hardware / Sensors
に以下の Simulink ブロックが格納されています．
「${\tt *** IMU Sensor}$」とい名前の Simulink ブロックが IMU センサ用です．これらのなかで，6 軸センサの Simulink ブロックには，
- ${\tt Accel}$（あるいは ${\tt Acceleration}$）：加速度
- ${\tt Ang Rate}$（あるいは ${\tt Angular Rate}$）：角速度
という出力端子が，9 軸センサの Simulink ブロックには，これらに加えて
- ${\tt Mag Field}$（あるいは ${\tt Magnetic Field}$）：方位
という出力端子があります．
3.4.2 6 軸センサ MPU6050 用の Simulink ブロック
今回使用する 6 軸センサ MPU6050 用の Simulink ブロックは
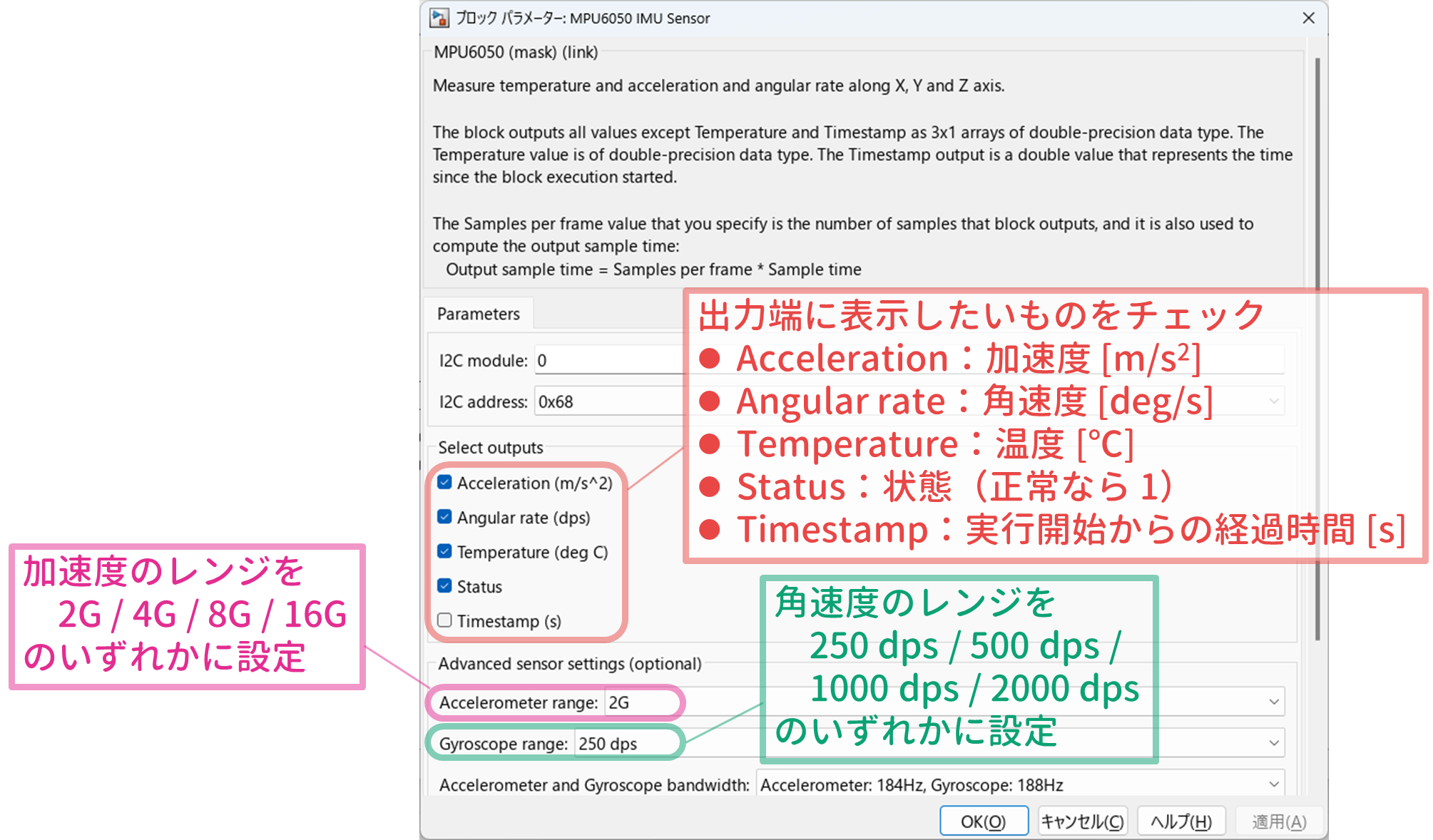
です．この Simulink ブロック ${\tt MPU6050\ IMU\ Sensor}$ をダブルクリックすると，
のように，いくつかのパラメータが設定できます．
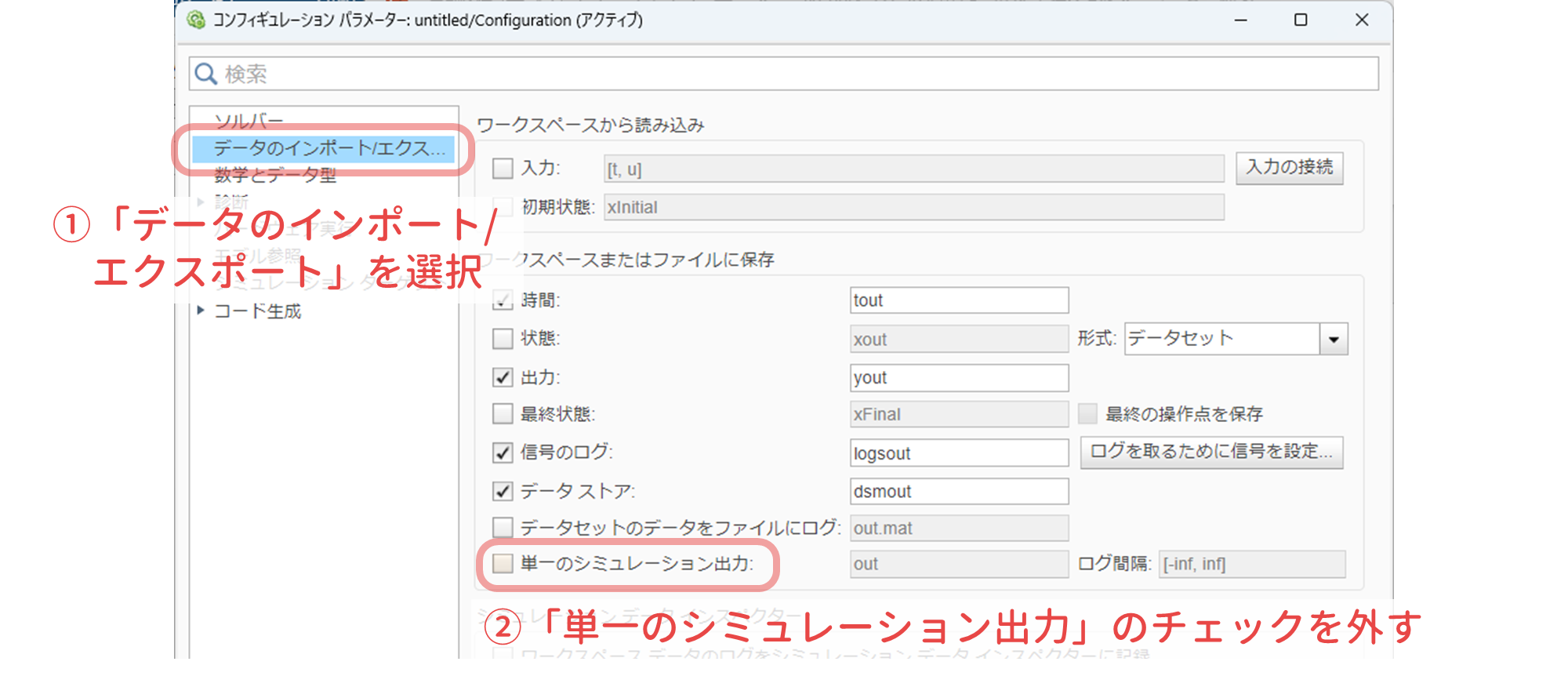
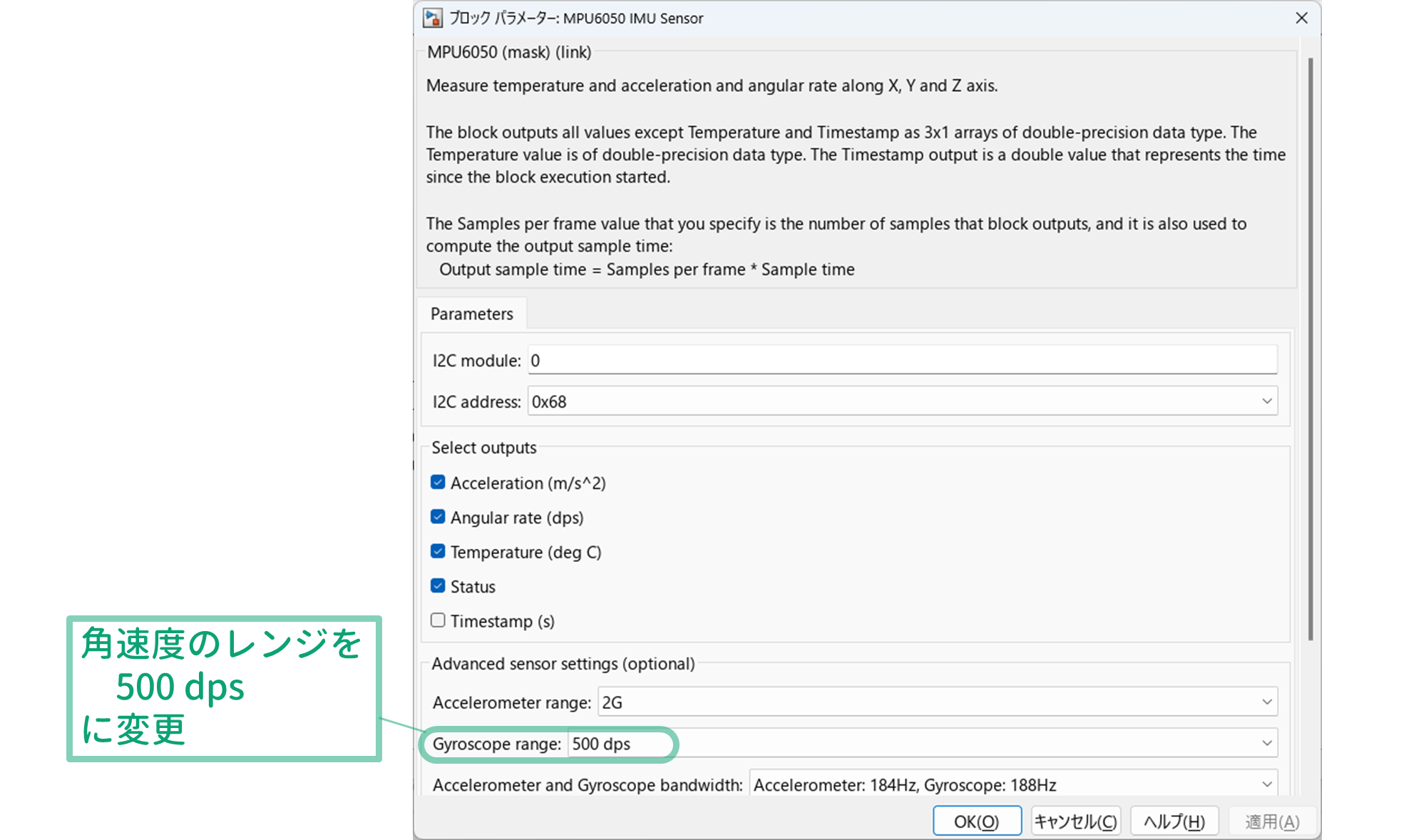
- Simulink ブロック ${\tt MPU6050\ IMU\ Sensor}$ の出力端に表示したいものにチェックを入れます．
- パラメータ ${\tt Accelerometer\ range}$ により加速度のレンジを 2G / 4G / 8G / 16G のいずれかに設定します（標準設定は 2G）．G は重力加速度 $g \simeq 9.8\ {\rm [m/s^2]}$ を意味しているので，2G と設定すればおおよそ $-19.6 \sim +19.6\ {\rm [m/s^2]}$ の範囲で，4G と設定すればおおよそ $-39.2 \sim +39.2\ {\rm [m/s^2]}$ の範囲で，$x$, $y$, $z$ 軸方向それぞれの加速度 $a_x$, $a_y$, $a_z$ を測定することができます．レンジを大きくするに従い広い範囲のデータを取得できますが，データは粗くなります（レンジを 2 倍にするとデータは 2 倍粗くなります）．
- パラメータ ${\tt Gyroscope\ range}$ により角速度のレンジを 250 dps / 500 dps / 1000 dps / 2000 dps のいずれかに設定します（標準設定は 250 dps）．dps は角速度の単位 deg/s を意味しているので，250 dps と設定すればおおよそ $-250 \sim +250\ {\rm [deg/s]}$ の範囲で，$x$, $y$, $z$ 軸まわりのそれぞれの角速度 $\omega_x$, $\omega_y$, $\omega_z$ を測定することができます．レンジを大きくするに従い広い範囲のデータを取得できますが，データは粗くなります（レンジを 2 倍にするとデータは 2 倍粗くなります）．
3.4.3 加速度と角速度を検出してみよう！
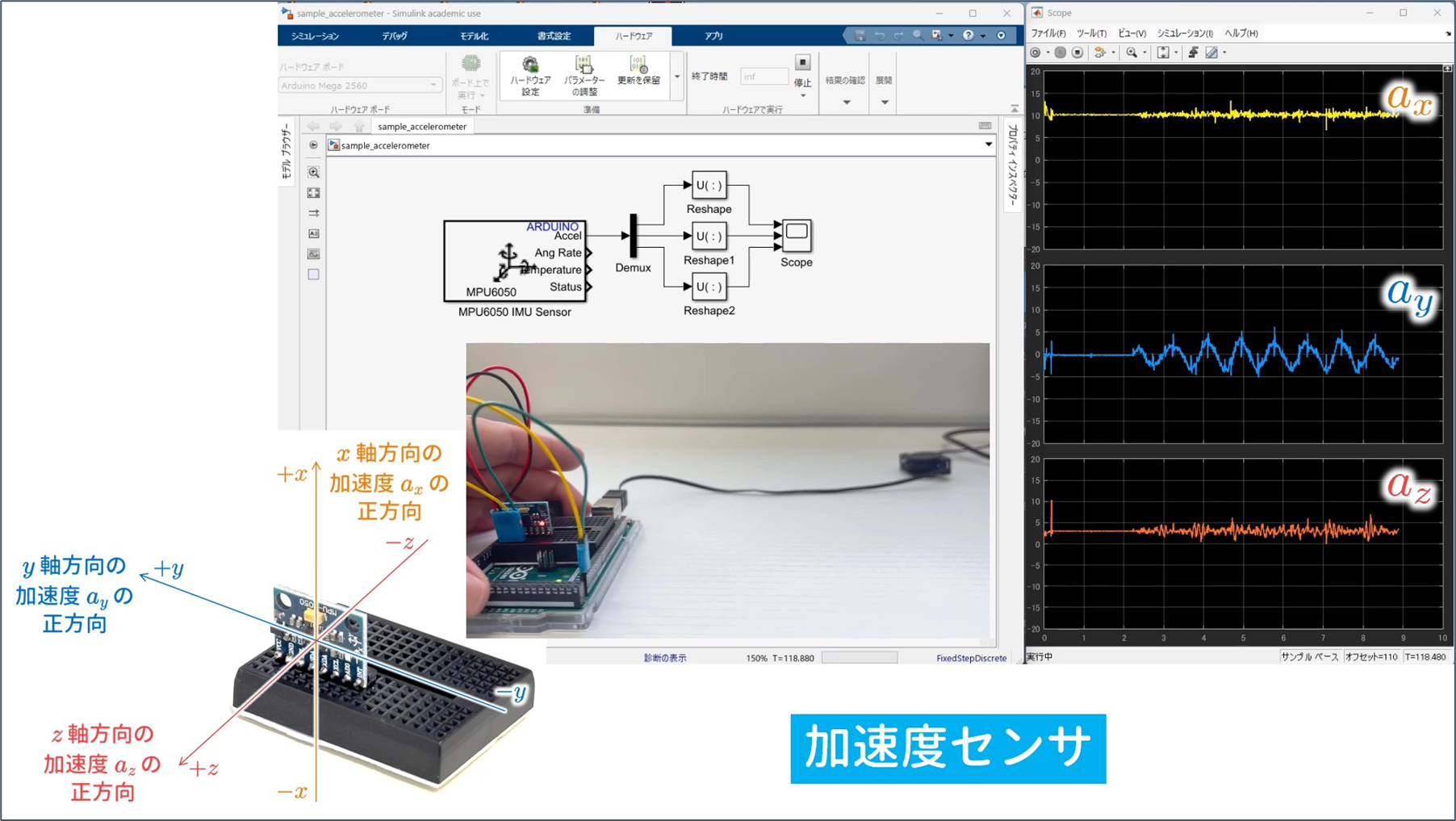
それでは，6 軸センサ MPU6050により加速度や角速度を検出するための Simulink モデルを作成してみましょう．
(a) Arduino Mega を動かすための Simulink モデルの基本設定
ステップ 1
空の Simulink モデルを開きます．
ステップ 2
Simulink モデルの空白部分を右クリックし，コンフィギュレーションパラメータを表示します．そして，以下のように設定します．
Arduino Mega の互換ボードを使用しているとき，上記の設定（COM ポート番号を「Automatically（自動設定）」）により Simulink モデルを実行すると，エラーを生じることがあります．このような場合は，以下の手順で手動で COM ポート番号を手動で設定してみてください．
(b) 角速度の検出
配布する角速度 $\omega_x$, $\omega_y$, $\omega_z$ $\rm{[deg/s]}$ を検出する Simulink モデル
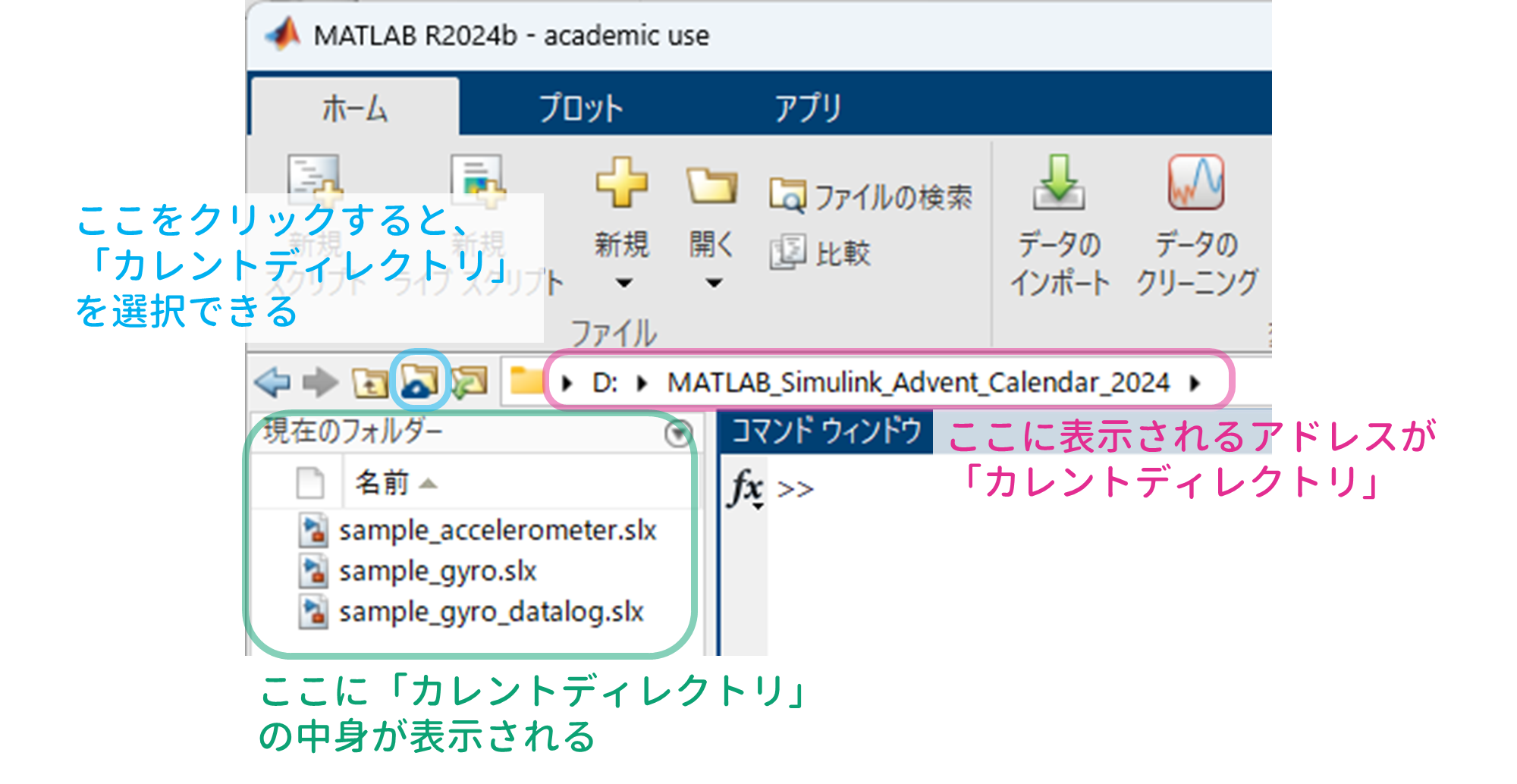
- $\verb+sample_gyro.slx+$
を開いてください．また，カレントディレクトリをこの Simulink モデルが保存されているフォルダに変更してください（以下，他の Simulink モデルを実行する場合も同様です）．
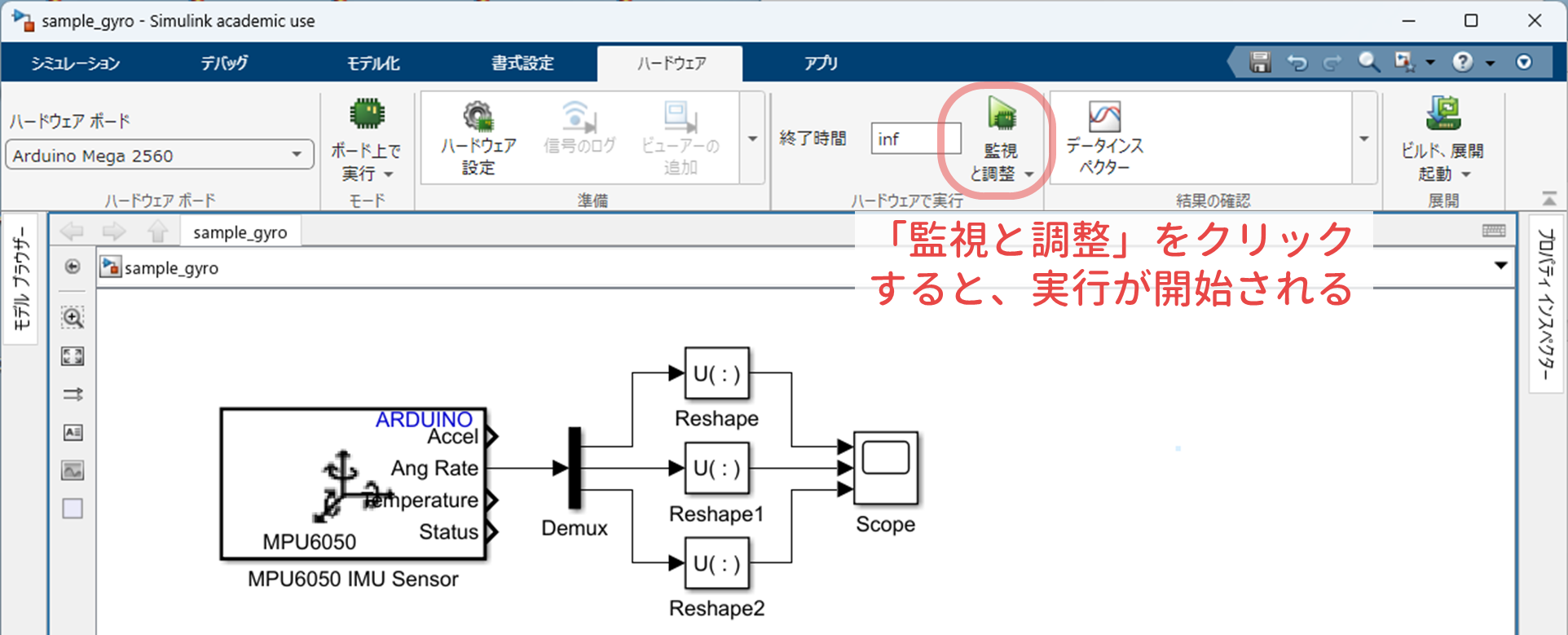
そして，この Simulink モデルの「監視と調整」をクリックして実行すると，以下のようになります（画像をクリックすると，YouTube 動画にジャンプします）．
以下の点に注意してください．
角速度のレンジは標準の 250 dps ($250\ {\rm deg/s}$) としていますが，速く動かす場合は下図のように頭打ちとなるので，500 dps ($500\ {\rm deg/s}$) などの大きな値に変更する必要があります．
以下，Simulink ブロック ${\tt MPU6050\ IMU\ Sensor}$ のパラメータ（加速度レンジ）を 500 dps に変更して使用します．
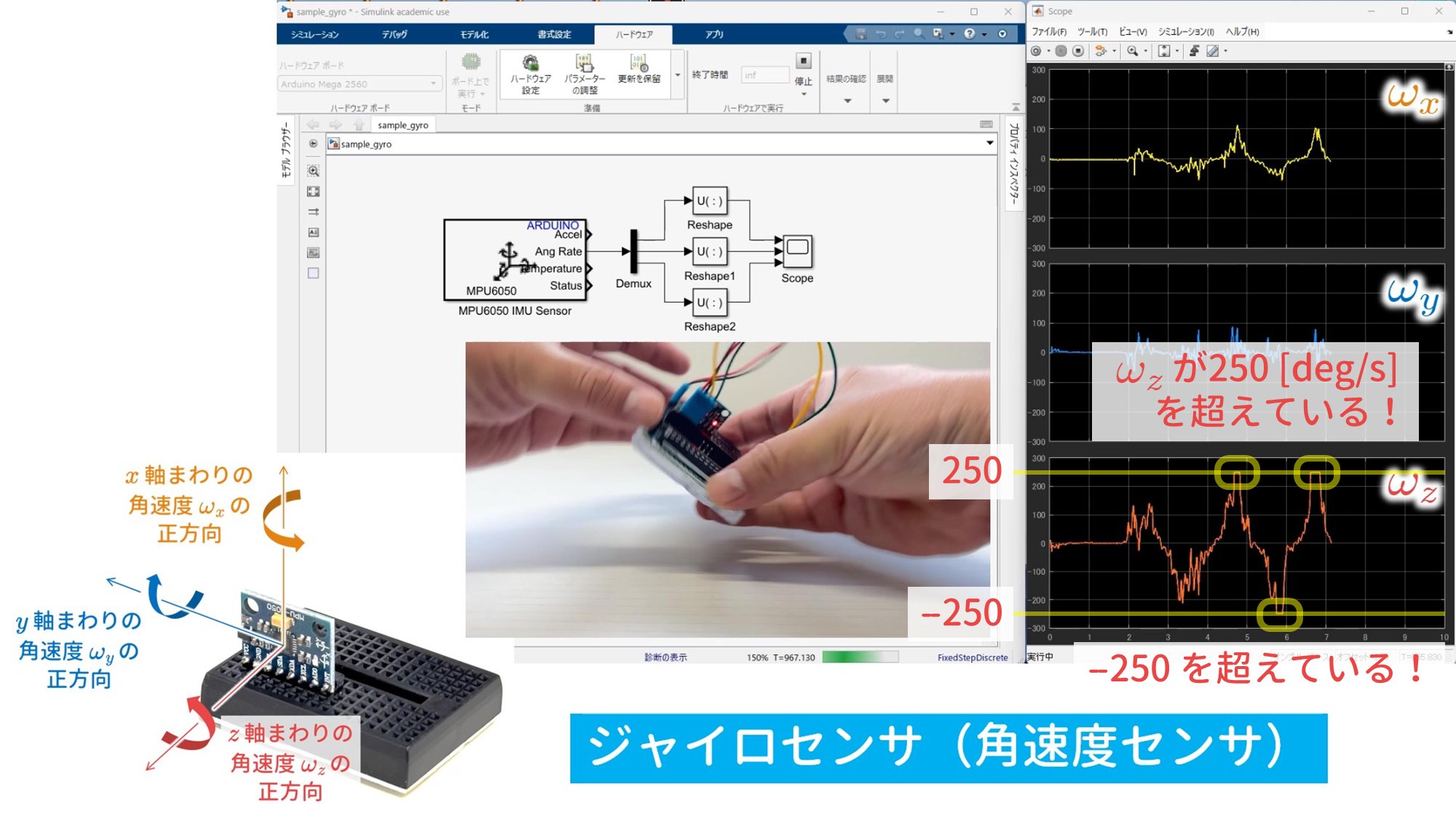
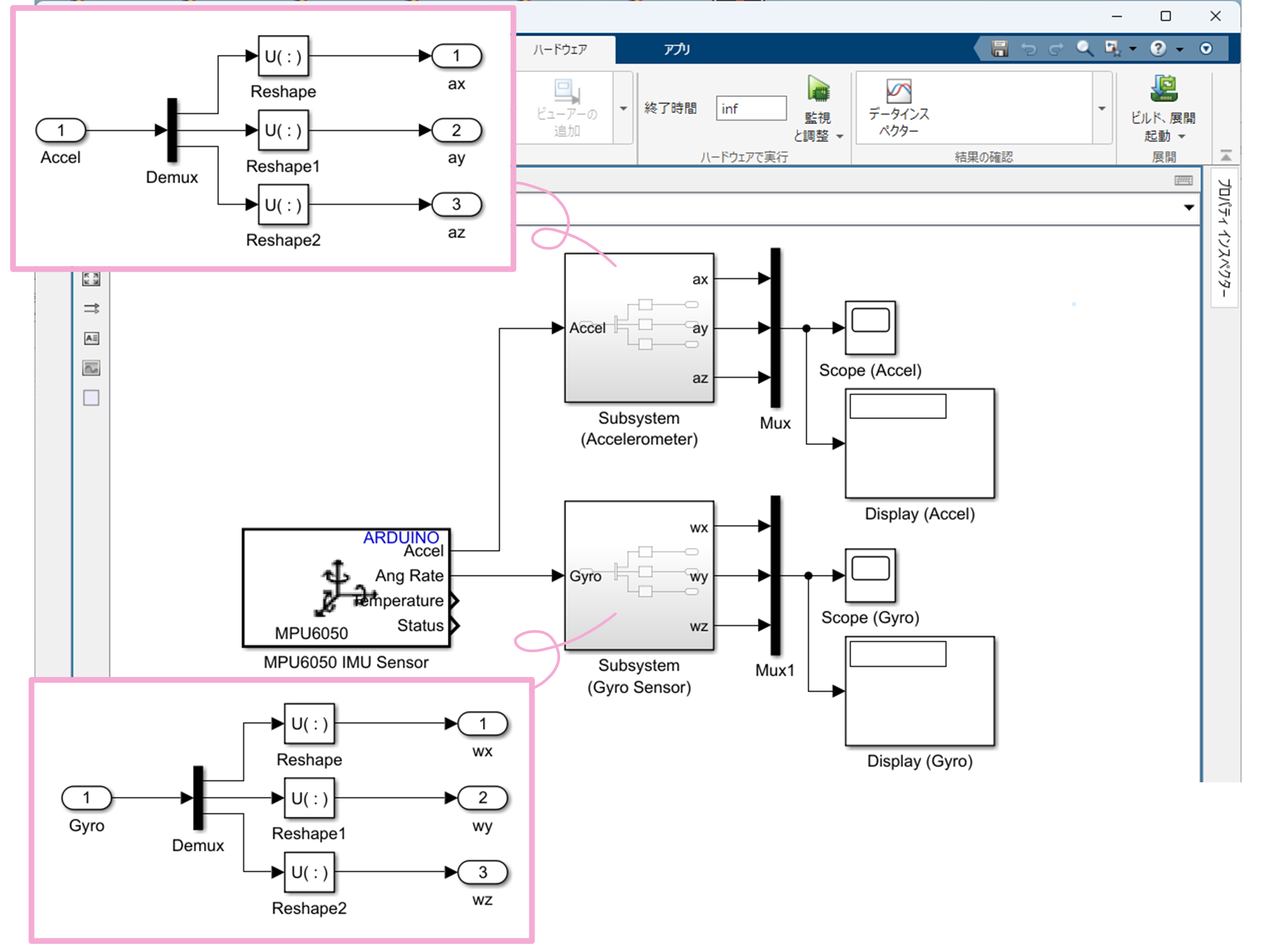
Simulink ブロック ${\tt MPU6050\ IMU\ Sensor}$ の出力端 ${\tt Ang\ Rate}$ の信号は角速度 $\omega_x$, $\omega_y$, $\omega_z$ $\rm{[deg/s]}$ がベクトル化された double 型の $3 \times 1 \times N$ の 3 次元配列なので，Simulink ブロック ${\tt Demux}$ によりこれらを分解し，3 つの $1 \times 1 \times N$ の 3 次元配列とします．さらに，Simulink ブロック ${\tt Reshape}$ により $N \times 1$ の 1 次元配列に変換します．
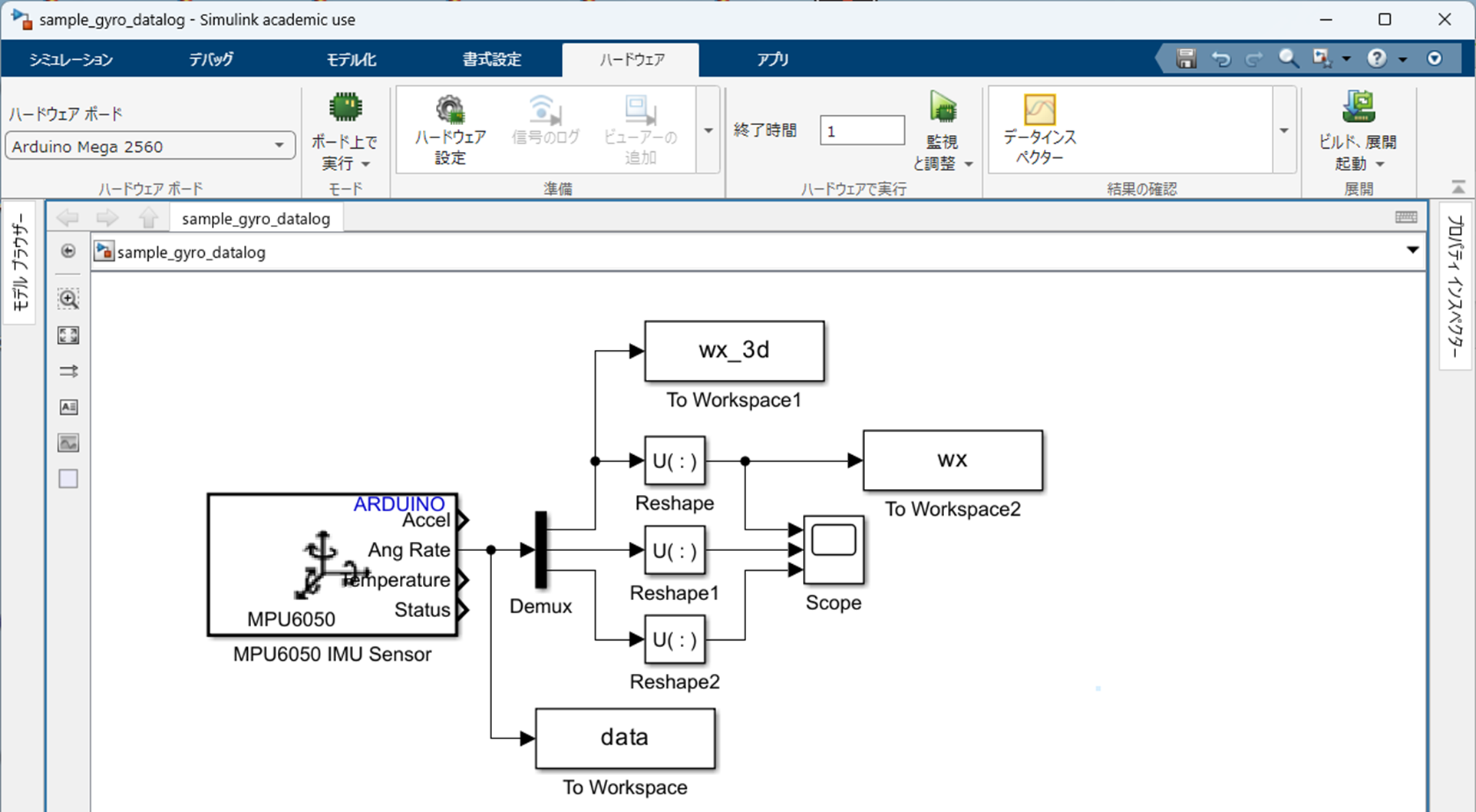
このことを確認するために，
- $\verb+sample_gyro_datalog.slx+$
を実行してみます．ただし，3 つの Simulink ブロック ${\tt To\ Workspace}$ の「保存形式」を「時系列」から「配列」に変更しています．また，Simulink モデルの終了時間を「${\tt inf}$」から「${\tt 1}$」に変更しています．この Simulink モデルを実行した後，MATLAB のコマンドウィンドウで ${\tt data}$, $\verb+wx_3d+$, ${\tt wx}$ のサイズを確認すると，以下のようになります．
>> size(data)
ans =
3 1 201
>> data
data(:,:,1) =
2.7008
37.4298
32.9056
data(:,:,2) =
1.4496
35.6369
29.9301
~~~~~~~~~~~ < 略 > ~~~~~~~~~~~
data(:,:,201) =
-11.4975
-9.3231
-30.2277
>> size(wx_3d)
ans =
1 1 201
>> wx_3d
wx_3d(:,:,1) =
2.7008
wx_3d(:,:,2) =
1.4496
~~~~~~~~~~~ < 略 > ~~~~~~~~~~~
wx_3d(:,:,201) =
-11.4975
>> size(wx)
ans =
201 1
>> wx
wx =
2.7008
1.4496
~~~~~~~~~~~ < 略 > ~~~~~~~~~~~
-11.4975
(c) 加速度の検出
配布する加速度 $a_x$, $a_y$, $a_z$ $\rm{[m/s^2]}$ を検出する Simulink モデル
- $\verb+sample_accelerometer.slx+$
を実行すると，以下のようになります（画像をクリックすると，YouTube 動画にジャンプします）．
加速度のレンジは標準の 2G としていますが，速く動かす場合は頭打ちとなるので，4G などの大きな値に変更する必要があります．
Simulink ブロック ${\tt MPU6050\ IMU\ Sensor}$ の出力端 ${\tt Accel}$ の信号は加速度 $a_x$, $a_y$, $a_z$ $\rm{[m/s^2]}$ がベクトル化された double 型の $3 \times 1 \times N$ の 3 次元配列なので，Simulink ブロック ${\tt Demux}$ によりこれらを分解し，3 つの $1 \times 1 \times N$ の 3 次元配列とします．さらに，Simulink ブロック ${\tt Reshape}$ により $N \times 1$ の 1 次元配列に変換します．
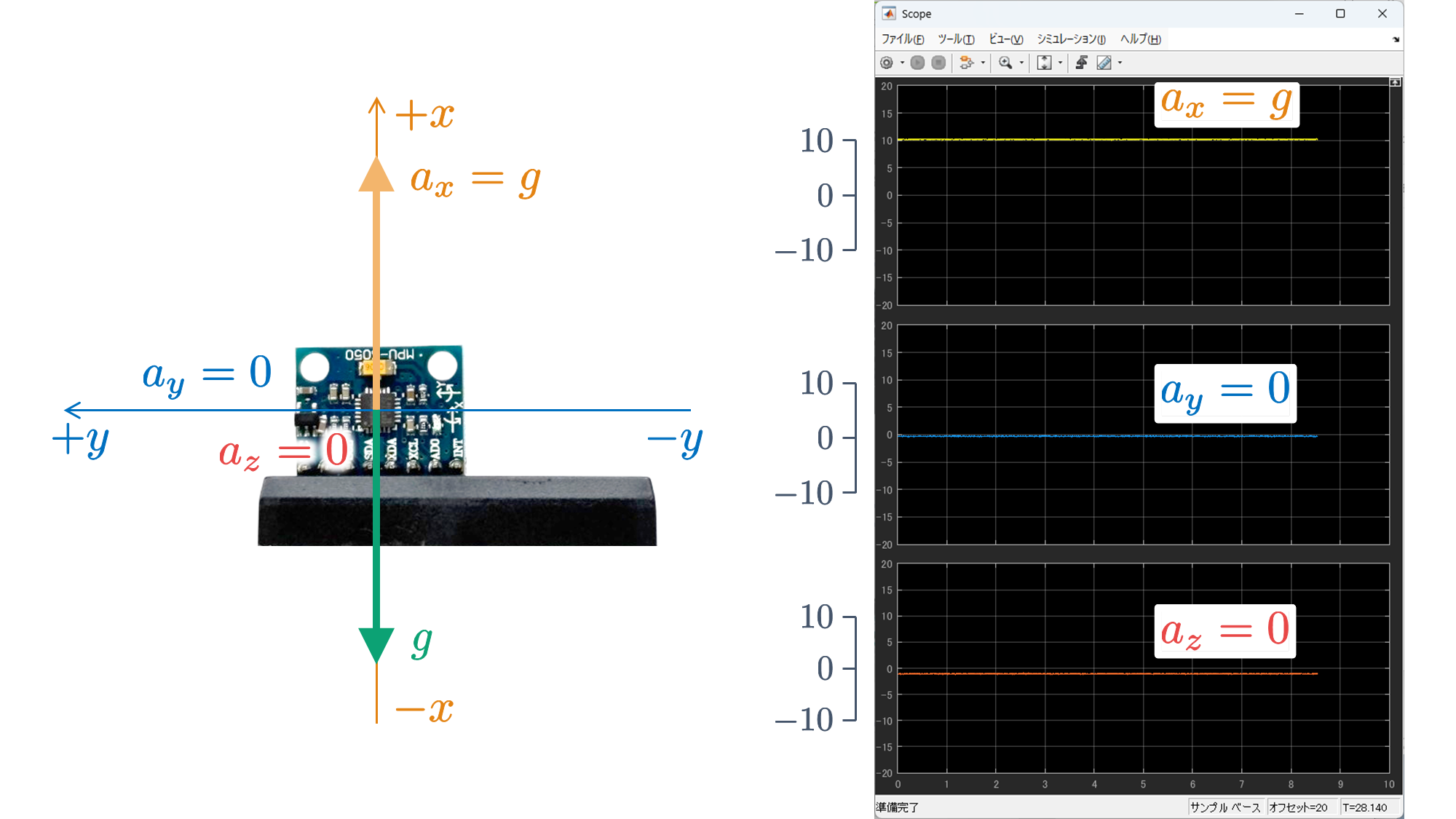
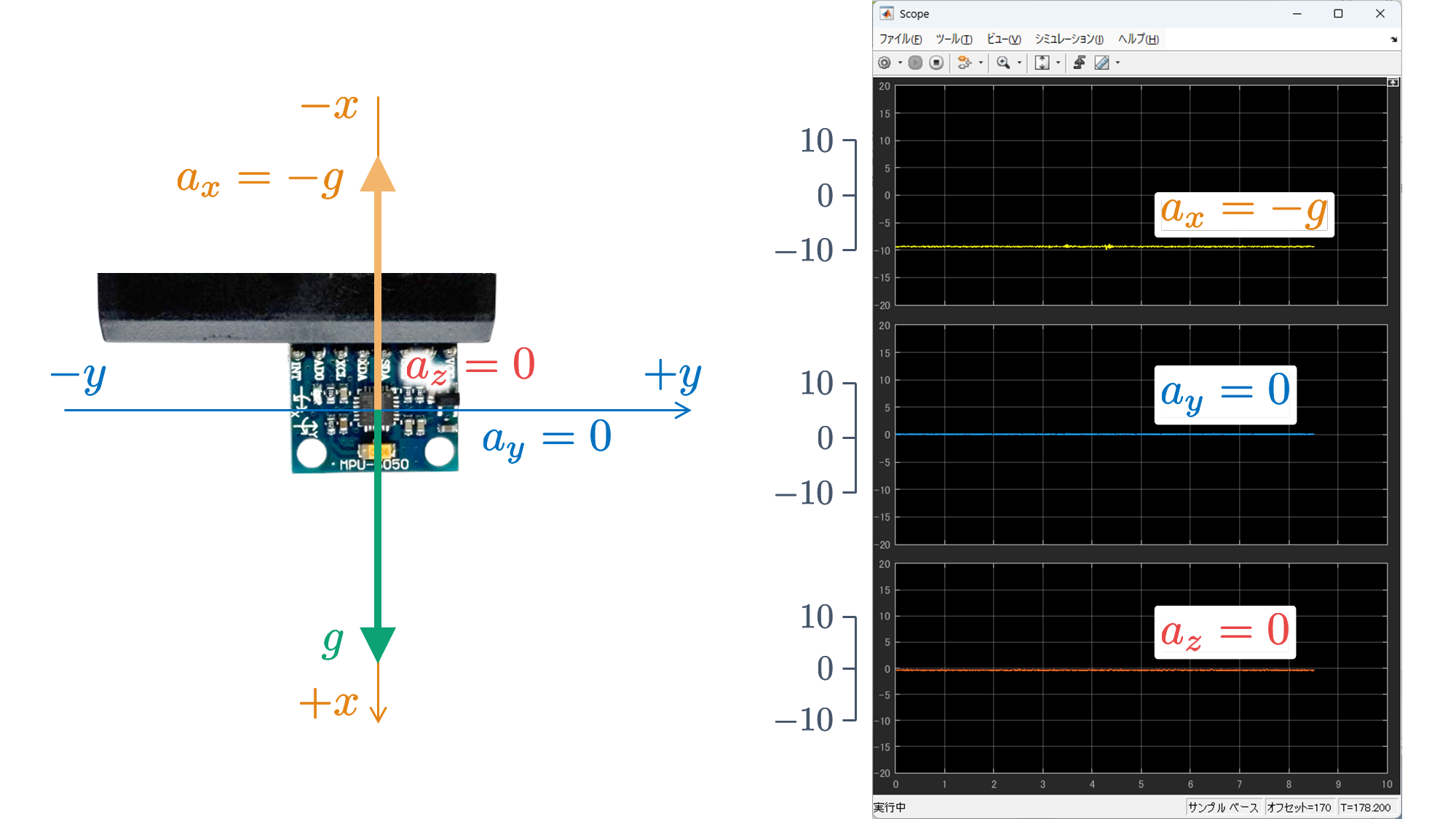
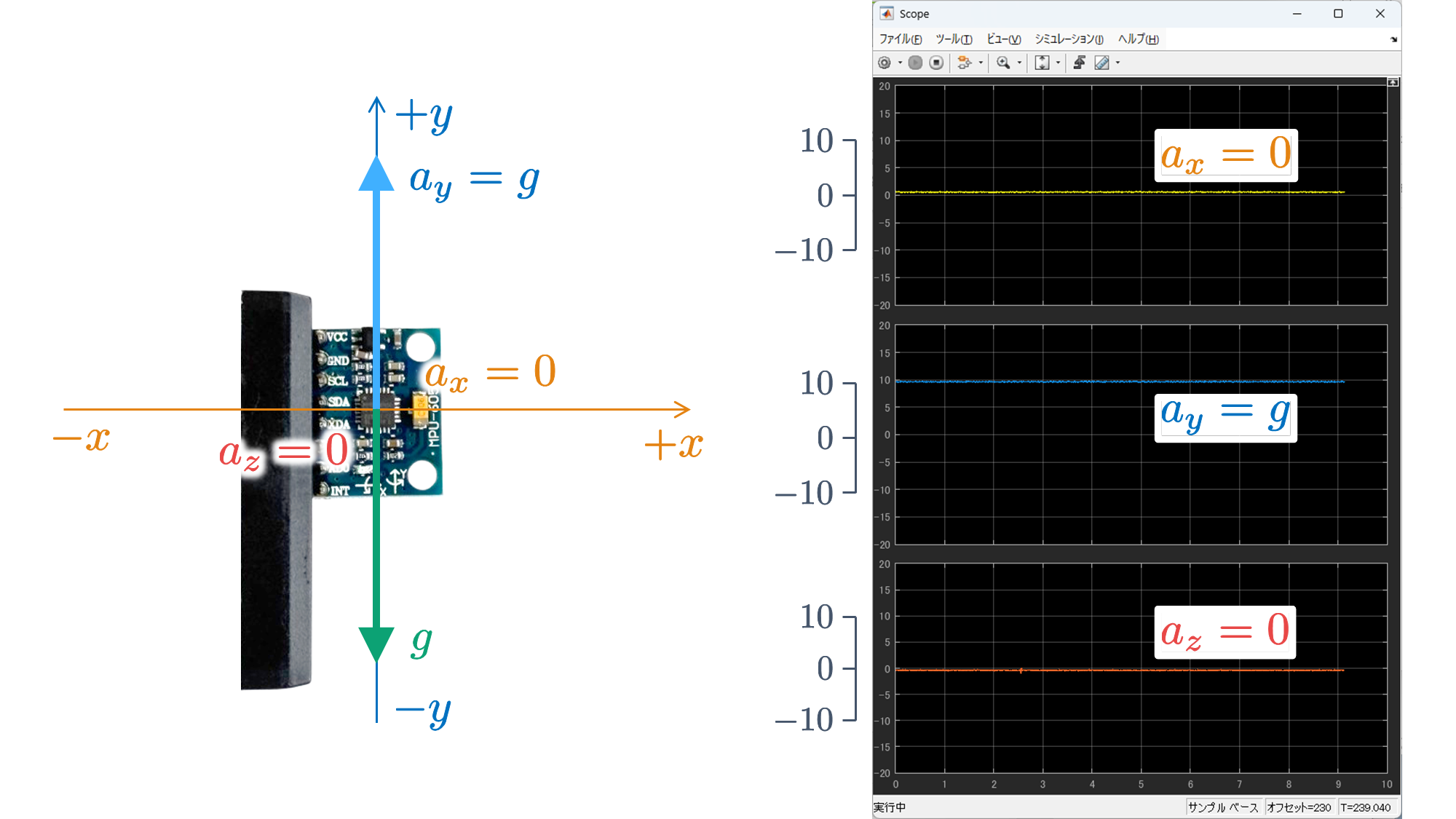
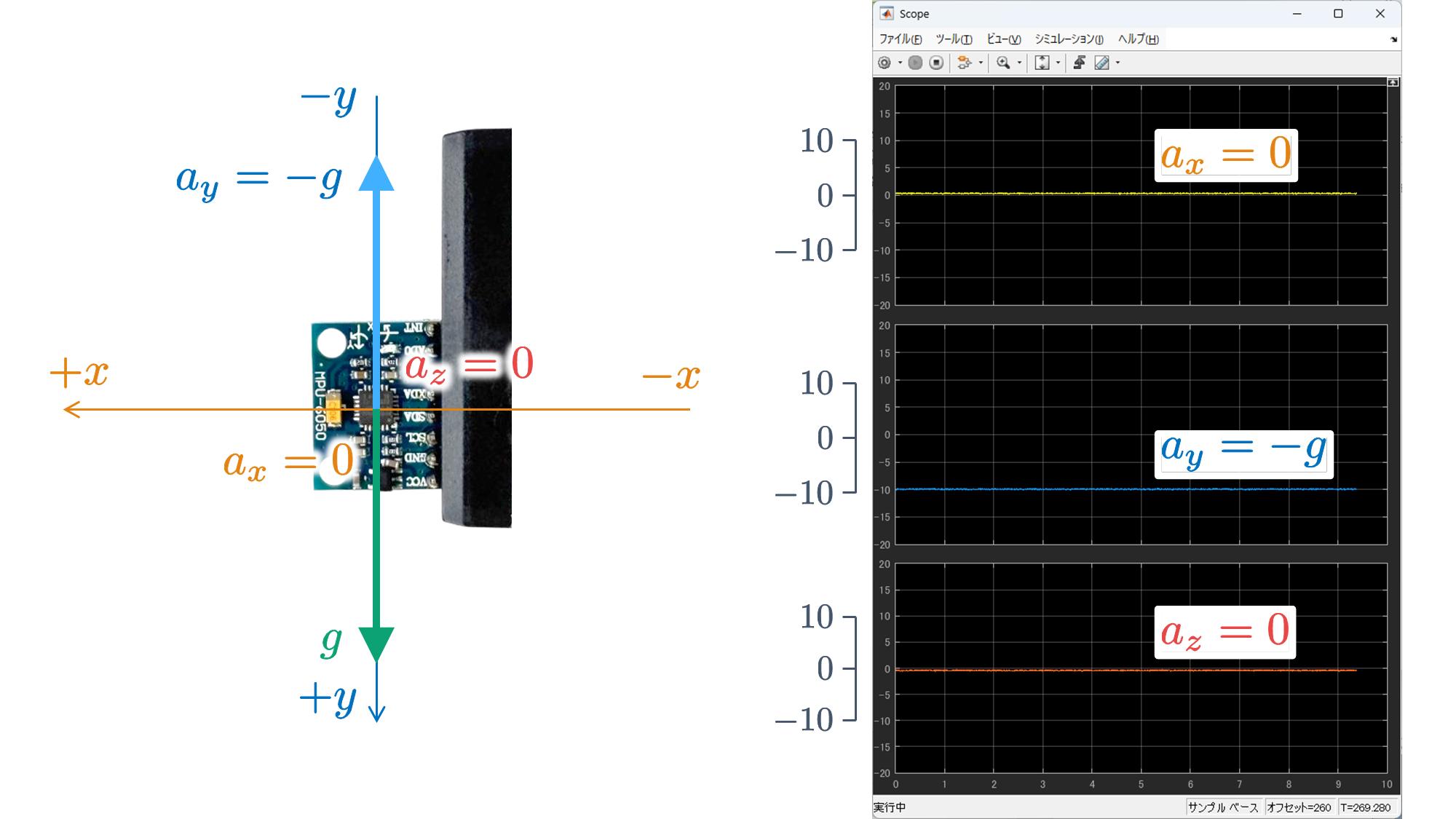
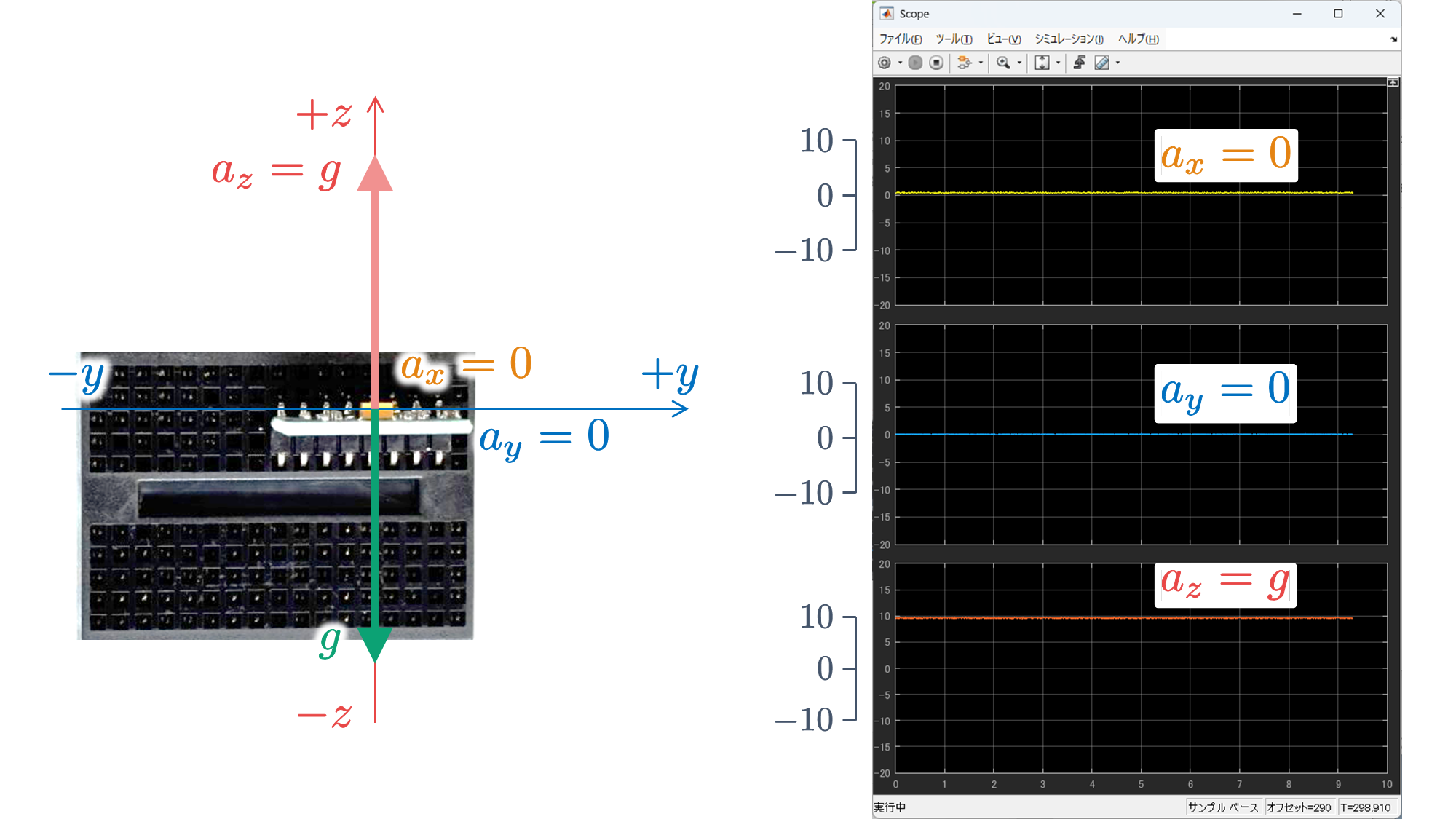
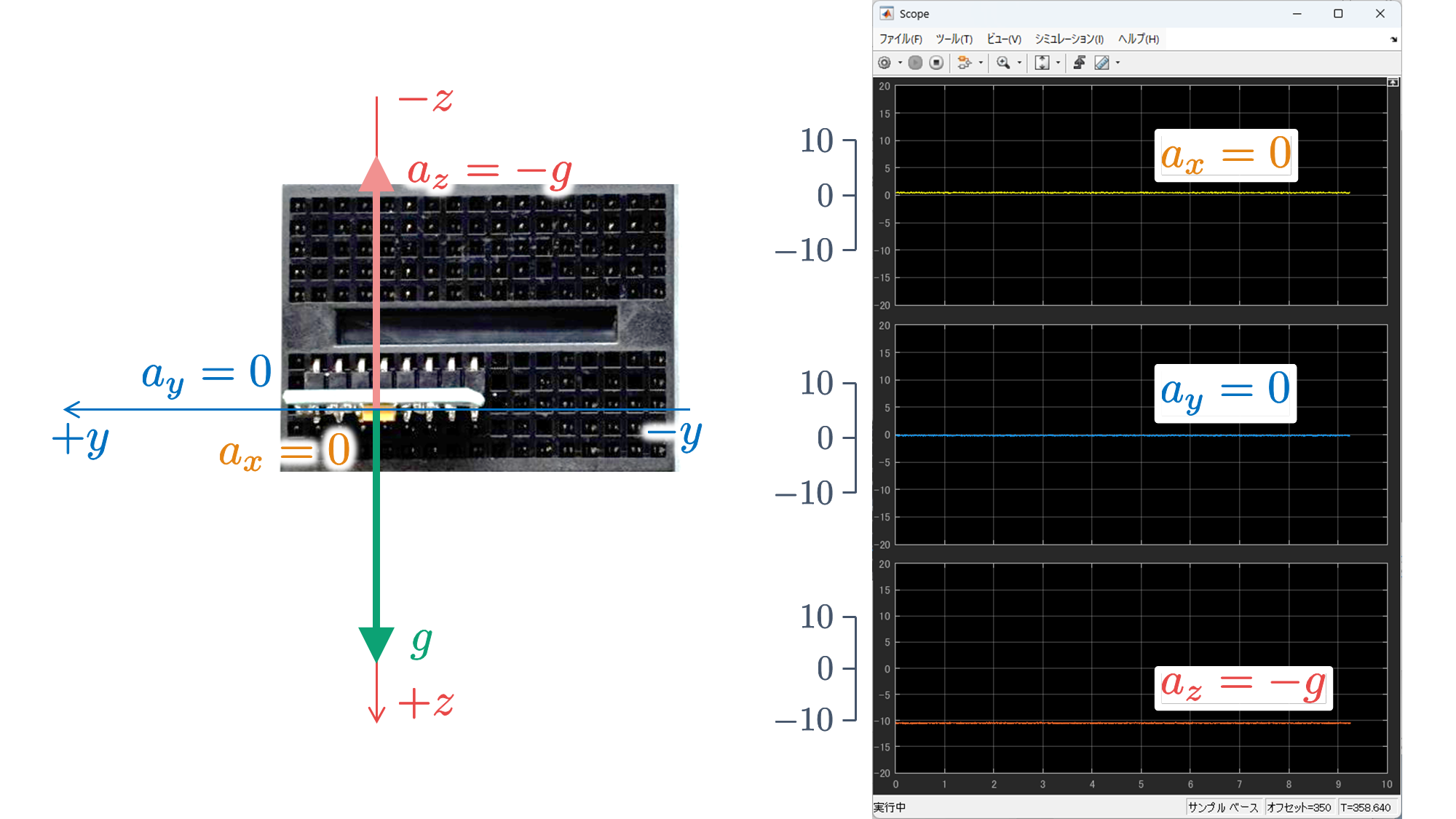
さて，実験したときに気づいたかもしれませんが，6 軸センサ MPU6050 を動かさずに静止させた状態であっても，加速度 $a_x$, $a_y$, $a_z$ は 0 であるとは限りません．これは，重力加速度 $g$ の影響を受けているからです．
試しに，Simulink モデル
- $\verb+sample_accelerometer.slx+$
を実行し，6 軸センサ MPU6050 が搭載されたブレッドボードの 6 つの面のいずれかが床面でとなるように静止させると，以下のような結果が得られます．
これらの結果から，重力加速度 $g$ に抗っている垂直抗力（向きが重力加速度 $g$ と反対の加速度）を検出していることがわかります．そのため，実際の動作の加速度にオフセット分（DC 成分）が含まれたものを検出していることがわかります．
3.4.4 キャリブレーションを行おう！
Simulink モデル
- $\verb+imu01_mpu6050.slx+$
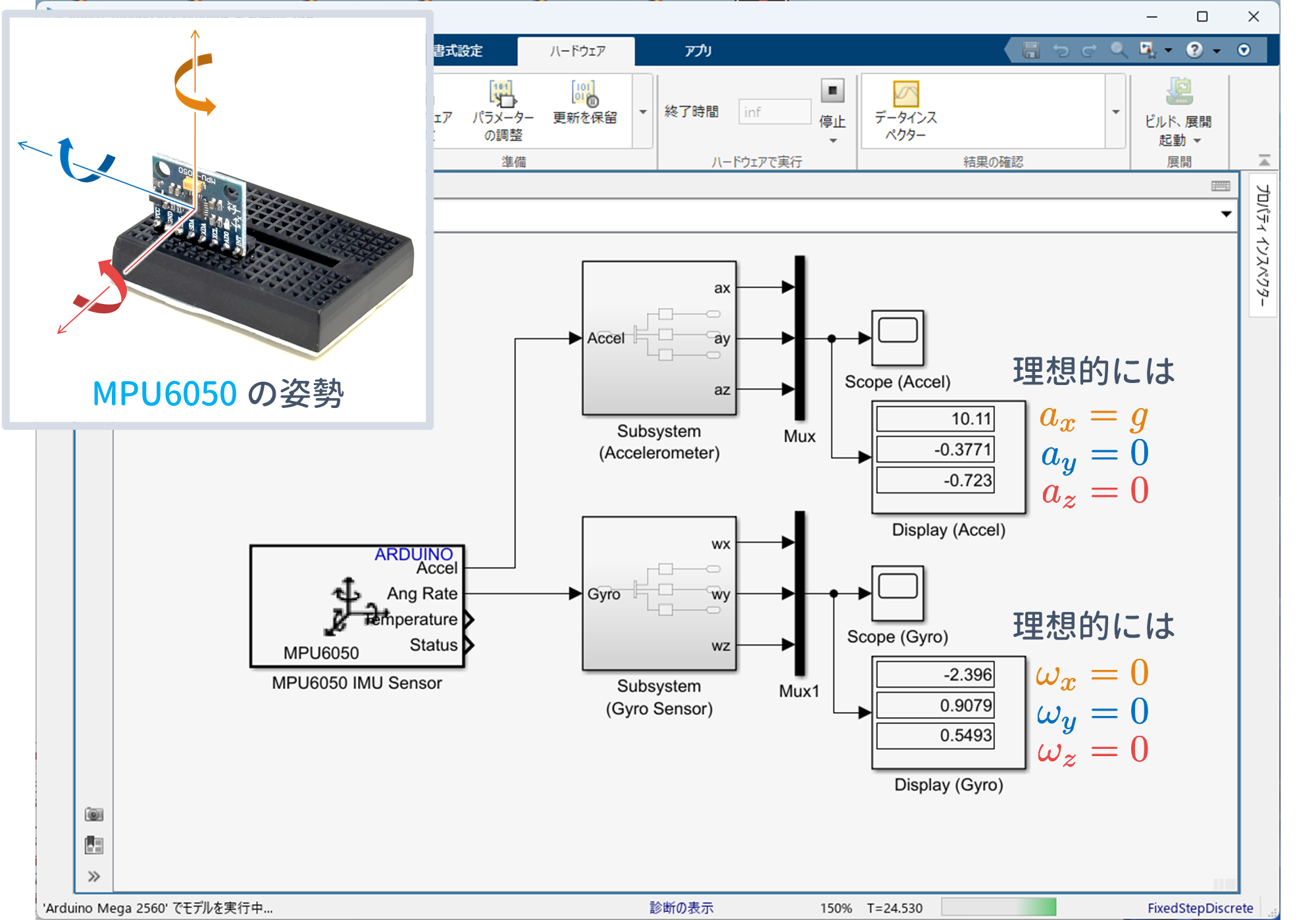
を実行してみましょう．実行すると，
のようになり，理想的な値からは少々ずれていることがわかります．この誤差を補正しないで後述の角度算出を行うと，悪影響を及ぼしてしまいます．
そこで，測定誤差を補正する「キャリブレーション (calibration)」という作業を行います．以下に，キャリブレーションの手順を示します．
ステップ 1
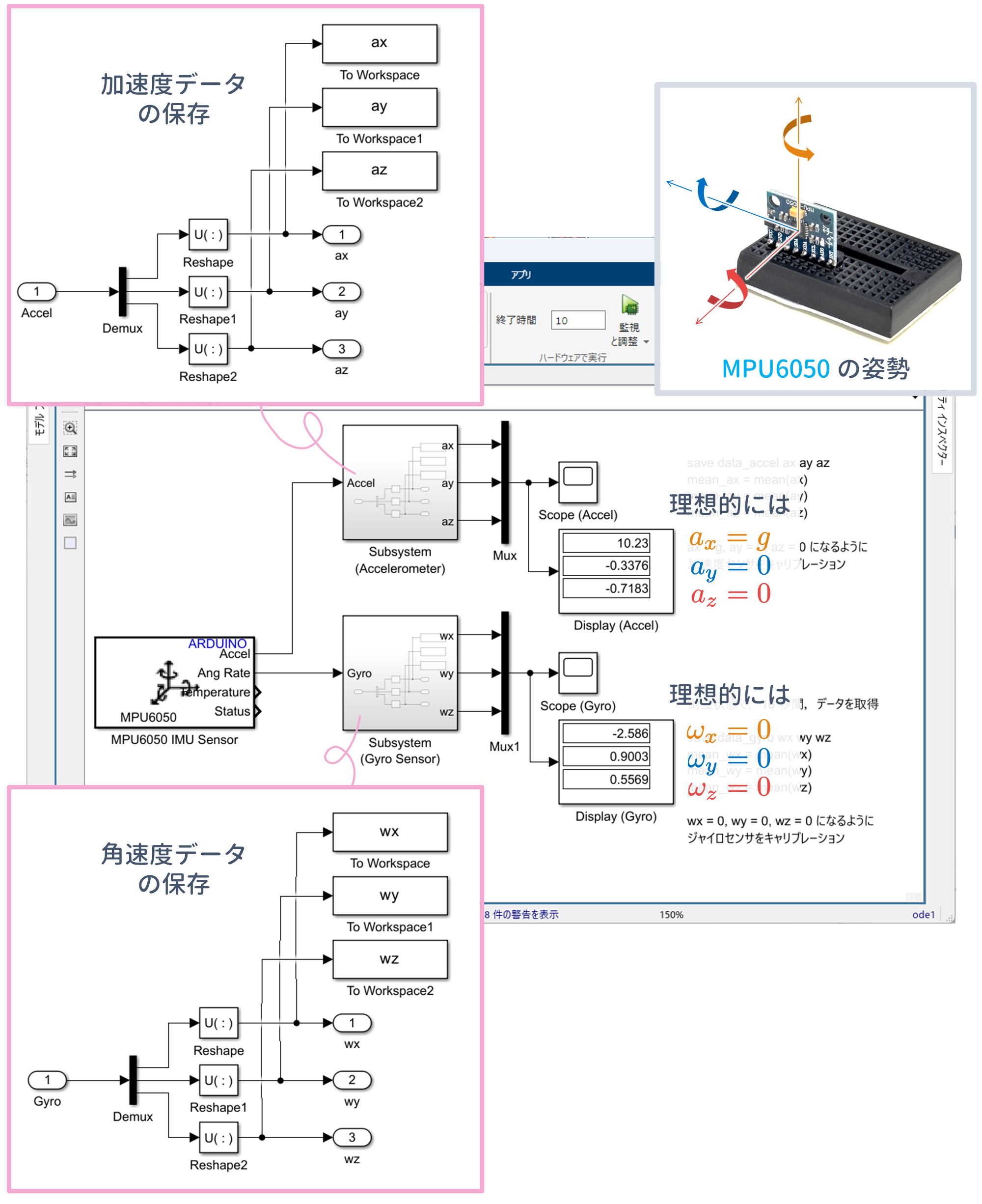
6 軸センサ MPU6050 が搭載されているブレッドボードを水平に静止させた状態で，Simulink モデル
- $\verb+imu02_mpu6050_datalog.slx+$
を実行します．この Simulink モデルは 10 秒間の実行が行われ，
のように加速度データ $a_x$, $a_y$, $a_z$ $\rm{[m/s^2]}$ と角速度データ $\omega_x$, $\omega_y$, $\omega_z$ $\rm{[deg/s]}$ がワークスペースに保存されます．そして，これらをそれぞれ $\verb+data_accel.mat+$, $\verb+data_gyro.mat+$ という名前の mat ファイルで保存するため，以下のように入力します．
>> save data_accel ax ay az % data_accel.mat の保存
>> save data_gyro wx wy wz % data_gyro.mat の保存
ステップ 2
コマンドウィンドウで
>> load data_accel
>> mean_ax = mean(ax)
mean_ax =
10.1848
>> mean_ay = mean(ay)
mean_ay =
0.0922
>> mean_az = mean(az)
mean_az =
-1.2272
と入力し，mat ファイル $\verb+data_accel.mat+$ を読み込み，また，加速度 $a_x$, $a_y$, $a_z$ $\rm{[m/s^2]}$ の基準値 $\verb+mean_x_a+$, $\verb+mean_y_a+$, $\verb+mean_z_a+$ を計算します．
同様に，コマンドウィンドウで
>> load data_gyro
>> mean_wx = mean(wx)
mean_wx =
-2.9691
>> mean_wy = mean(wy)
mean_wy =
0.9323
>> mean_wz = mean(wz)
mean_wz =
0.6750
と入力し，mat ファイル $\verb+data_gyro.mat+$ を読み込み，また，加速度 $\omega_x$, $\omega_y$, $\omega_z$ $\rm{[deg/s]}$ の基準値 $\verb+mean_x_g+$, $\verb+mean_y_g+$, $\verb+mean_z_g+$ を計算します．
ステップ 3
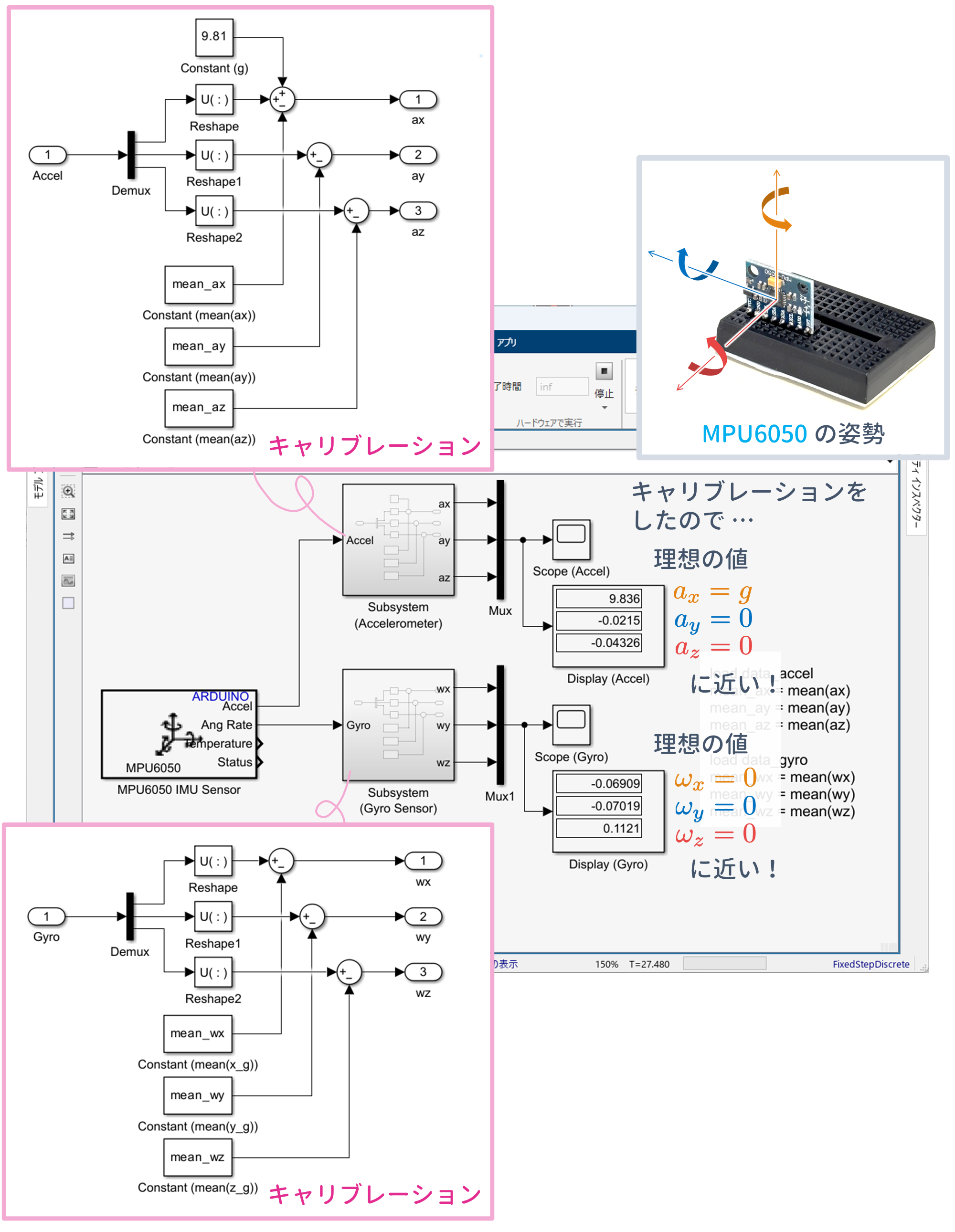
6 軸センサ MPU6050 が搭載されているブレッドボードを水平に静止させた状態で，Simulink モデル
- $\verb+imu03_mpu6050_calibration.slx+$
を実行します．その結果，以下のように基準値が理想の値に近くなることが確認できます．
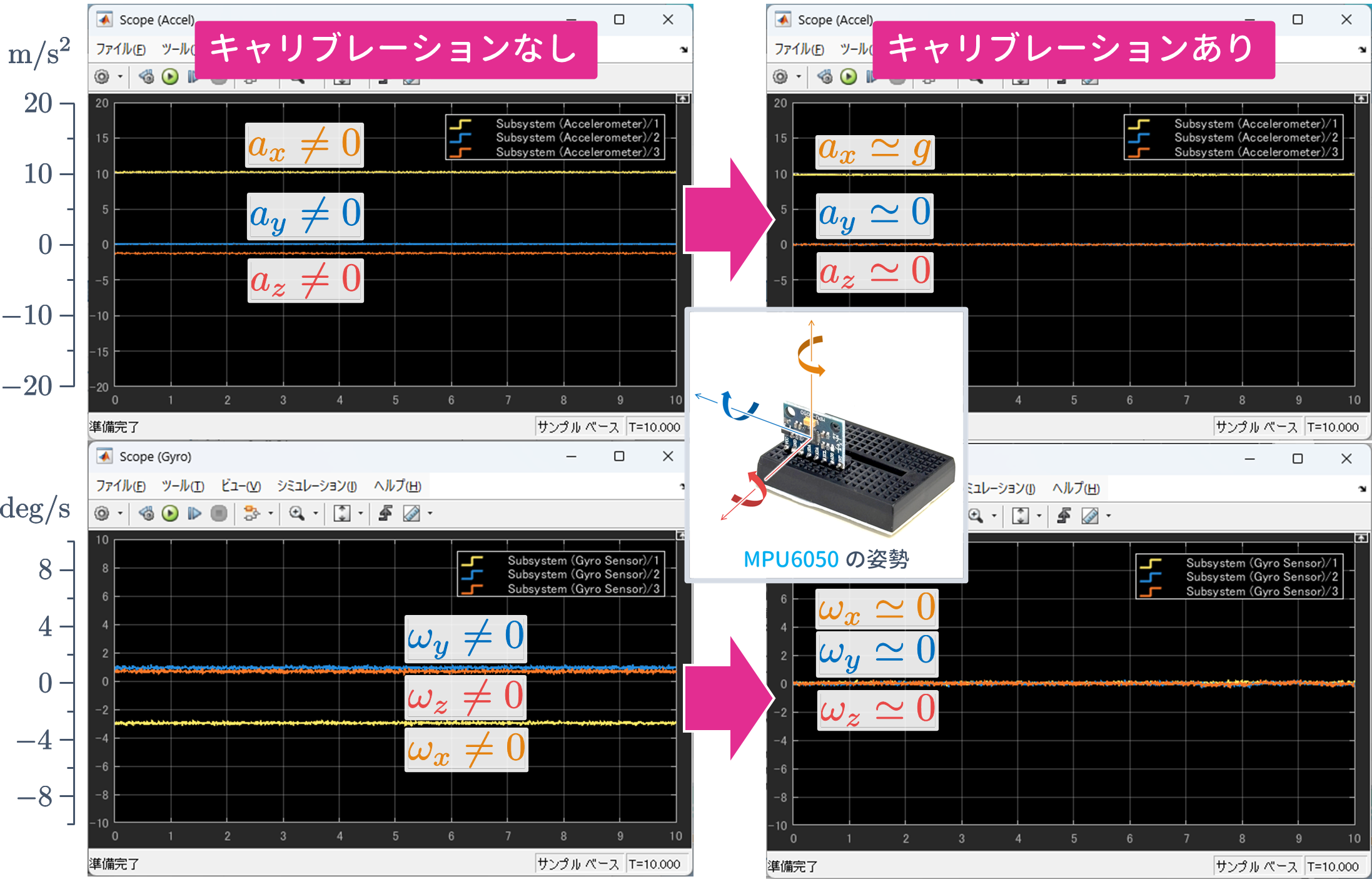
Simulink モデル
- $\verb+imu04_mpu6050_calibration_datalog.slx+$
を実行して，キャリブレーションを行った後の加速度データ $a_x$, $a_y$, $a_z$ $\rm{[m/s^2]}$ と角速度データ $\omega_x$, $\omega_y$, $\omega_z$ $\rm{[deg/s]}$ を，10 秒間，検出しました．このときのデータを mat ファイル $\verb+data_cal_accel.mat+$, $\verb+data_cal_gyro.mat+$ に保存し，平均を求めると，以下のようになります．
>> save data_cal_accel ax ay az
>> mean_cal_ax = mean(ax)
mean_cal_ax =
9.8107
>> mean_cal_ay = mean(ay)
mean_cal_ay =
0.0103
>> mean_cal_az = mean(az)
mean_cal_az =
-1.6805e-04
>> save data_cal_gyro wx wy wz
>> mean_cal_wx = mean(wx)
mean_cal_wx =
0.0406
>> mean_cal_wy = mean(wy)
mean_cal_wy =
-0.0086
>> mean_cal_wz = mean(wz)
mean_cal_wz =
0.0019
また，Scope で観測した結果を以下に示します．
3.5 6 軸センサにより 3 軸まわりの角度がわかるの？
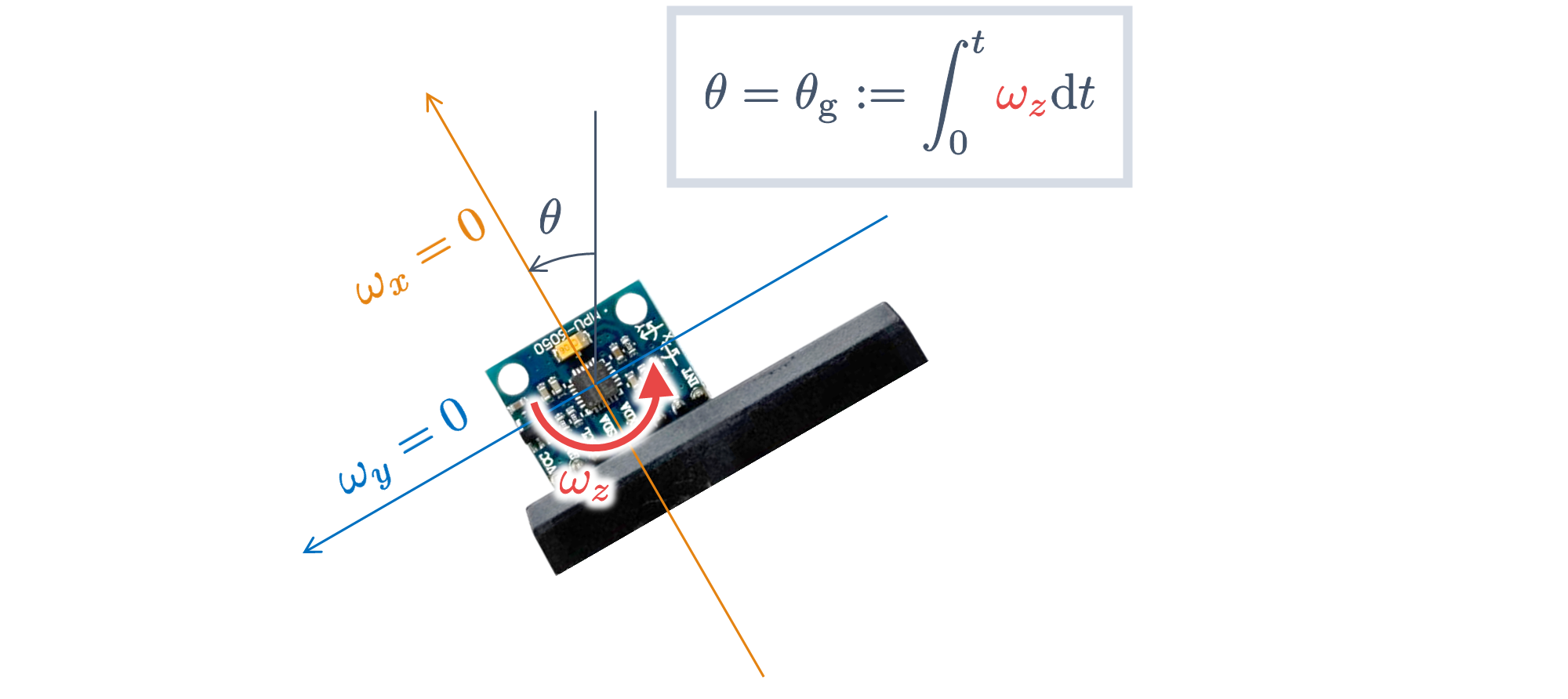
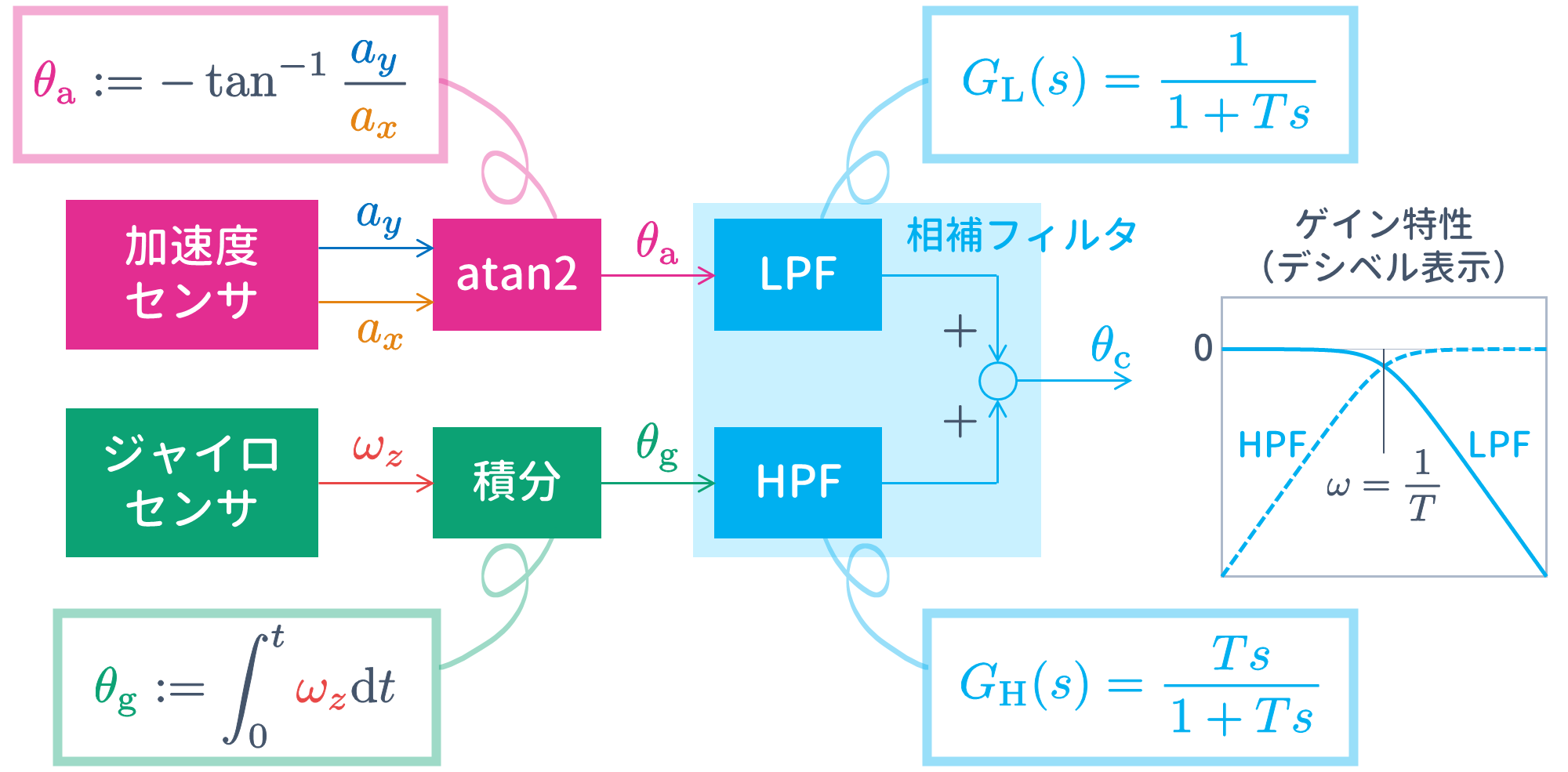
ここでは，一例として，$\pmb{z}$ 軸まわりの角度 $\pmb{\theta}$ を算出する方法について検討します．
3.5.1 ジャイロセンサの値から角度を算出してみる
理想的には，ジャイロセンサで検出される角速度 $\omega_z(t) = \dot{\theta}_g(t)$ を
\begin{align}
\theta(t) = \theta_{\rm g}(t) := \int_0^t\omega_z(t) {\rm d}t
\tag{1}
\end{align}
のように積分することで，$z$ 軸まわりの角度 $\theta_{\rm g}(t)$ を算出することができます．
しかし，
- 初期姿勢が基準姿勢からズレている $(\theta_{\rm g}(0) \neq 0)$
- キャリブレーションが適切ではなく，角速度 $\omega_z(t)$ が $\delta$ ほどズレている（バイアスが $\delta$）
という状況下では，積分値は
\begin{align}
\int_0^t(\omega_z(t) + \delta){\rm d}t
= \theta_{\rm g}(t) - \theta_{\rm g}(0) + {\delta}t
\tag{2}
\end{align}
となります．したがって，
- $\theta_{\rm g}(0)$ ほどズレてしまう
- ドリフト ${\delta}t$ を生じてしまう
ということが問題となります．
それでは，Simulink モデル
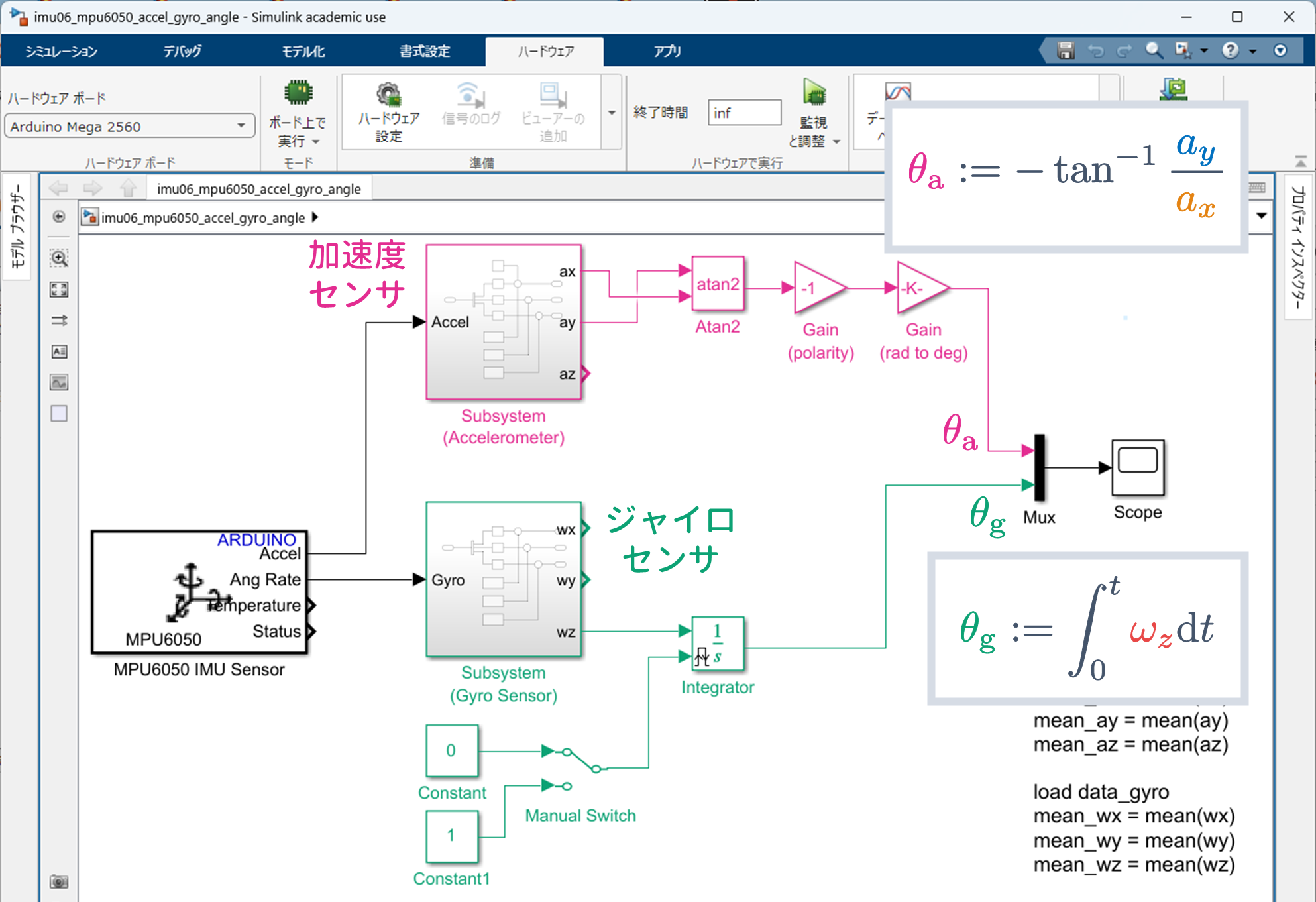
- $\verb+imu05_mpu6050_gyro_angle.slx+$
を以下に示す条件で動作させ，ジャイロセンサの特性を確認してみましょう．
ジャイロセンサによる角度算出（キャリブレーションあり，初期姿勢が水平）
まず，先に行ったキャリブレーションによる補正を行います．
>> load data_gyro
>> mean_wx = mean(wx);
>> mean_wy = mean(wy);
>> mean_wz = mean(wz);
そして，6 軸センサ MPU6050 が搭載されているブレッドボードを水平にし，Simulink モデル $\verb+imu05_mpu6050_gyro_angle.slx+$ を実行してください．
イイ感じに角度が算出できていますね！
ジャイロセンサによる角度算出（キャリブレーションあり，初期姿勢が水平ではない）
つぎに，6 軸センサ MPU6050 が搭載されているブレッドボードを少し傾けてから Simulink モデル $\verb+imu05_mpu6050_gyro_angle.slx+$ を実行してください．
初期角度が $\theta_{\rm g}(0) \neq 0$ なので，ジャイロセンサでは，ここを基準とした角度を算出してしまっていることがわかります．
ジャイロセンサによる角度算出（キャリブレーションなし，初期姿勢が水平）：ドリフト現象
ジャイロセンサのキャリブレーションを行わないと，どうなるでしょうか．まず，$z$ 軸まわりの角速度の補正値を
>> mean_wz = 0;
のように，リセットします．そして，6 軸センサ MPU6050 が搭載されているブレッドボードを水平にして，Simulink モデル $\verb+imu05_mpu6050_gyro_angle.slx+$ を実行すると，
のように，ドリフト項 $\pmb{{\delta}t}$ の影響が現れることがわかります．
3.5.2 加速度センサの値から角度を算出してみる
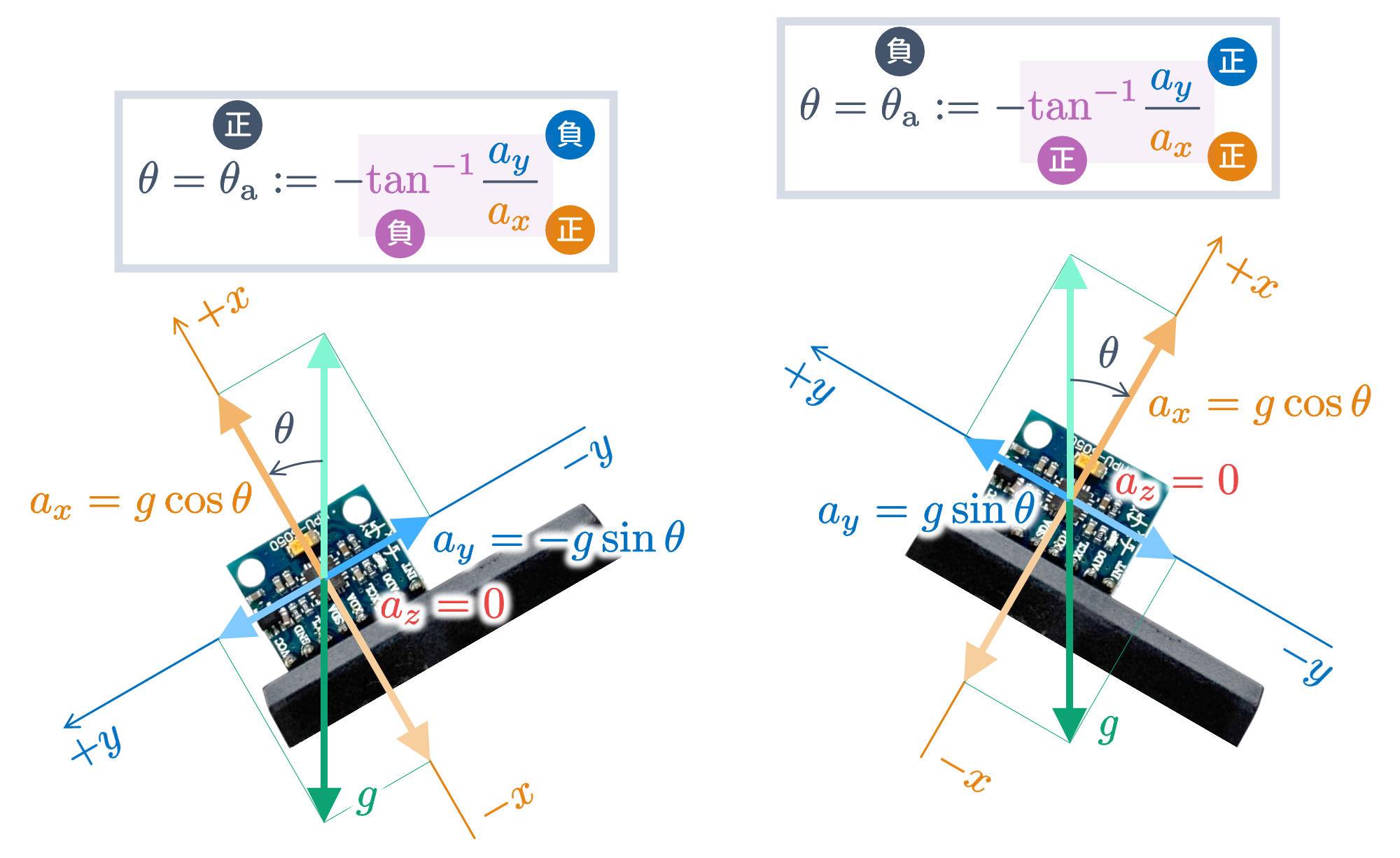
加速度センサをゆっくりと動かしているとき，加速度はほぼ重力 $g$ のみです．このような状況下では，
\begin{align}
&
\tan\theta_{\rm a}(t)
= \dfrac{a_x}
{a_y}
\\
&
\quad \Longrightarrow \quad
\theta(t) = \theta_{\rm a}(t)
:= -\tan^{-1}\dfrac{a_x}{a_y}
\tag{3}
\end{align}
により $z$ 軸まわりの角度 $\theta_{\rm a}(t)$ を算出することができます．
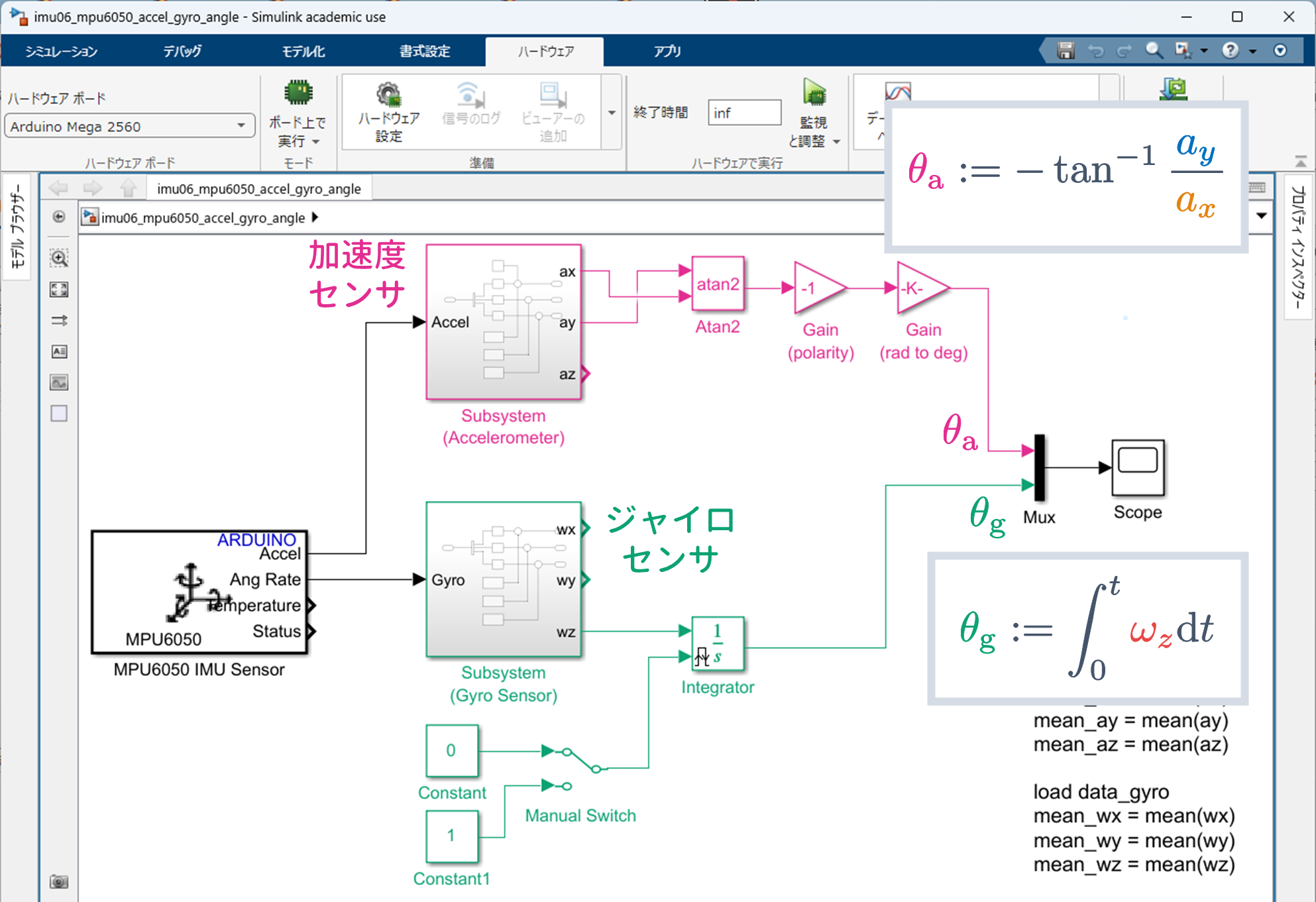
Simulink モデル
- $\verb+imu06_mpu6050_accel_gyro_angle.slx+$
を以下に示す条件で動作させ，加速度センサの特性を確認してみましょう．
加速度センサによる角度算出（キャリブレーションあり，初期姿勢が水平）
まず，先に行ったキャリブレーションによる補正を行います．
>> load data_gyro
>> mean_wx = mean(wx);
>> mean_wy = mean(wy);
>> mean_wz = mean(wz);
>> load data_accel
>> mean_ax = mean(ax);
>> mean_ay = mean(ay);
>> mean_az = mean(az);
そして，6 軸センサ MPU6050 が搭載されているブレッドボードを水平にして，Simulink モデル $\verb+imu06_mpu6050_accel_gyro_angle.slx+$ を実行してください．
このように，ゆっくりと動かしたとき，加速度センサにより算出された角度 $\theta_{\rm a}$ は，ジャイロセンサにより算出された角度 $\theta_{\rm g}$ と似通った形状であることが確認できます．ただし，加速度センサを用いると，高周波ノイズの影響が大きいことが確認できます．
加速度センサによる角度算出（キャリブレーションあり，初期姿勢が水平）：振動を加える
高周波成分が問題となることを確認するために，6 軸センサ MPU6050 が搭載されているブレッドボードを水平で静止させている姿勢で，ブレッドボードを叩いて衝撃を与えてみます．
このように，加速度センサは振動に過敏に反応して，インパルス状の信号を出していることがわかります．一方で，ジャイロセンサはこのような振動に強いことも確認できます．
加速度センサによる角度算出（キャリブレーションあり，初期姿勢が水平ではない）
つぎに，6 軸センサ MPU6050 が搭載されているブレッドボードを少し傾けてから Simulink モデル $\verb+imu06_mpu6050_accel_gyro_angle.slx+$ を実行してください．
ジャイロセンサと異なり，加速度センサでは，初期姿勢に依存せずに角度を算出できることが確認できます．
加速度センサによる角度算出（加速度センサのキャリブレーションなし，ジャイロセンサのキャリブレーションあり，初期姿勢が水平）
さいごに，加速度センサのキャリブレーションを行わないと，どうなるかを確認しましょう．まず，$x$，$y$ 軸方向の加速度の補正値を
>> mean_ax = 0;
>> mean_ay = 0;
のように，リセットします．そして，Simulink モデル $\verb+imu06_mpu6050_accel_gyro_angle.slx+$ を実行すると，
のように，角度が正しく算出されません．これは，重力を $x$ 軸と $y$ 軸方向に分解したときの三角形が歪んでしまうからです．
3.5.3 相補フィルタによりイイ感じにセンサフュージョン
以上のことをまとめると，
-
加速度センサによる角度算出
- 低周波成分の信頼性が高い
- 高周波成分の信頼性が低い（高周波ノイズが問題）
-
ジャイロセンサによる角度算出
- 高周波成分の信頼性が高い
- 低周波成分の信頼性が低い（ゆっくりとズレるドリフト現象が問題）
という特徴があります．そこで，低周波の情報を得意とする加速度センサからは低周波成分を抽出し，高周波の情報を得意とするジャイロセンサからは高周波成分を抽出して，それぞれを加算します．具体的には，
\begin{align}
G_{\rm L}(s) + G_{\rm H}(s) = 1
\end{align}
を満足するローパスフィルタ (LPF)
\begin{align}
G_{\rm L}(s) = \dfrac{1}{1 + Ts}
\end{align}
とハイパスフィルタ (HPF)
\begin{align}
G_{\rm H}(s) = \dfrac{Ts}{1 + Ts}
\end{align}
を用い，次式により角度算出を行います．
相補フィルタ (Complementary Filter)
\begin{align}
\theta(t) = \theta_{\rm c}(t)
:= G_{\rm L}(s)\theta_{\rm a}(t)
+ G_{\rm H}(s)\theta_{\rm g}(t)
\tag{4}
\end{align}
このように，複数のセンサから得られるデータを統合し，単一のセンサでは得られない正確で信頼性の高い情報を生成する技術をセンサフュージョン (Sensor Fusion) といいます．
相補フィルタは，カルマンフィルタのような高度なアルゴリズムと比べて，計算量が少ないにもかかわらず，そこそこの実用的な結果が得られるという利点があります．
それでは，Simulink モデル
- $\verb+imu07_mpu6050_comp_filter_angle.slx+$
を以下に示す条件で動作させてみましょう．
相補フィルタによる角度算出（キャリブレーションあり，初期姿勢が水平）
まず，先に行ったキャリブレーションによる補正を行います．
>> load data_gyro
>> mean_wx = mean(wx);
>> mean_wy = mean(wy);
>> mean_wz = mean(wz);
>> load data_accel
>> mean_ax = mean(ax);
>> mean_ay = mean(ay);
>> mean_az = mean(az);
そして，Simulink モデル $\verb+imu07_mpu6050_comp_filter_angle.slx+$ を実行してください．
相補フィルタはイイ感じですね！
相補フィルタによる角度算出（キャリブレーションあり，初期姿勢が水平）
つぎに，6 軸センサ MPU6050 が搭載されているブレッドボードを少し傾けてから Simulink モデル $\verb+imu07_mpu6050_comp_filter_angle.slx+$ を実行してください．
相補フィルタは初期姿勢の影響を受けず，イイ感じですね！
相補フィルタによる角度算出（ジャイロセンサのキャリブレーションなし，加速度センサのキャリブレーションあり，初期姿勢が水平）
最後に，ジャイロセンサのキャリブレーションが適切でない場合，どうなるかを確認しましょう．まず，$z$ 軸まわりの角速度の補正値を
>> mean_wz = 0;
のように，リセットします．そして，6 軸センサ MPU6050 が搭載されているブレッドボードを水平にして， Simulink モデル $\verb+imu07_mpu6050_comp_filter_angle.slx+$ を実行すると，
となります．相補フィルタはドリフトの影響を受けず，イイ感じですね！
5. 倒立振子よ、今こそ立ち上がれ！
さて，いよいよ，倒立振子です！
今回は，セグウェイタイプの車輪型倒立振子を LEGO で製作し，コントローラを手動で調整して倒立させます．
5.1 車輪型 LEGO 倒立振子の組み立て
5.1.1 電子部品リスト (2024/12/06)
以下の電子部品を使用して車輪型倒立振子を製作しました．
| 型番 | メーカー | 購入先 | 価格 | |
|---|---|---|---|---|
|
【再掲】 マイコンボード |
Arduino Mega 2560 R3 | Arduino | RS | 5,940 円 |
|
【再掲】 6 軸センサ （はんだ付けオプション：L 字ピン） |
MPU6050 (GY-521) | - | 電子工作ステーション | 360 円 （+500 円） |
|
【再掲】 ミニブレッドボード |
BB-601 | - | 秋月電子通商 | 160 円 |
|
【再掲】 USB ケーブル（リールケーブル A-B タイプ） |
- | COMON(カモン) | amazon | 584 円 |
|
【再掲】 プロトタイプ開発用シールド |
DFR0131 | DFRobot |
digikey mouser |
2,116 円 2,137 円 |
| 基板用端子台 （2.54mm ピッチ 1 列 3 極） 【2 個必要】 |
790-1092 | RS PRO | RS | 174 円 |
| モータドライバ （はんだ付けオプション） |
DRV8833 | - | 電子工作ステーション | 150 円 （+500 円） |
| エンコーダ付ギヤード DC モータ （減速比 50:1，エンコーダ分解能 7PPR） 【2 個必要】 |
FIT0482 | DFRobot | digikey | 1,944 円 |
| モータブラケット（2 個入） | FIT0160 | DFRobot | digikey | 572 円 |
| 単 3 x 6 本用電池ボックス | Sitrda | amazon | 450 円 | |
| LEGO 用軸アダプタ付車輪 Black Multi-Hub Wheel for TT / Lego or N20 Motor - 65mm Diameter 【2 個必要】 |
4205 | Adafruit |
digikey mouser |
319 円 322 円 |
これ以外に，モータを固定するための
- M2 x 16mm バインド小ねじ：4 本
- M2 ワッシャー：2 個
や，ケーブルの延長のための
- ケーブル
- 熱圧縮チューブ
を使用しています．
5.1.2 車輪型倒立振子の LEGO 部品リストと組立図
さっそく，LEGO 部品を利用して，車輪型倒立振子のボディを製作してみましょう．
-
LEGO 部品のリストはこちら（PDF ファイル）です．
-
組立図はこちら（PDF ファイル）です．
この組立図をもとに組み立てた本体は，このようになります．
5.1.2 モータの LEGO 部品への取り付け
DFRobot のエンコーダ付ギヤード DC モータ FIT0482 とモータブラケット FIT0160 を，M2 のねじにより LEGO 部品 [40490] に取り付けます．モータブラケット FIT0160 にもねじが付属しているのですが，短いので，別途購入しました．
モータブラケットのねじ穴と LEGO 部品の穴の位置は少しだけずれているのですが，ねじを締めると固定できます（ねじが少し「ハの字」にはなります）．ねじは左右を少しずつ締めるようにしてください．
そして，下図に示すように，LEGO 部品 [32054] をモータブラケット FIT0160 の上部に押し付けてください．
また，LEGO 用軸アダプタ付車輪から軸アダプタを取り外し，モータ軸に取り付けてください．
最後に，モータケーブルの延長を行います．モータケーブルは 6 本の線で構成されていますが，これらのうち，
- 緑色 [$\tt{C1 (A)}$] の線（USB コネクタの逆側のモータ）
- 黄色 [$\tt{C2 (B)}$] の線（USB コネクタの逆側のモータ）
- 白色 [$\tt{M1 (M+)}$] の線（USB コネクタ側のモータ）
- 赤色 [$\tt{M2 (M\verb+-+)}$] の線（USB コネクタ側のモータ）
の長さが不足しています．そのため，
- 緑色 [$\tt{C1 (A)}$] の線と黄色 [$\tt{C2 (B)}$] の線は，手持ちの緑色，黄色のジャンパワイヤと「はんだ接続」をして延長（熱圧縮チューブで補強）
- 白色 [$\tt{M1 (M+)}$] の線と赤色 [$\tt{M2 (M\verb+-+)}$] の線は，手持ちの白色，赤色の線と「はんだ接続」をして延長（熱圧縮チューブで補強）
し，モータのコネクタに接続しました．
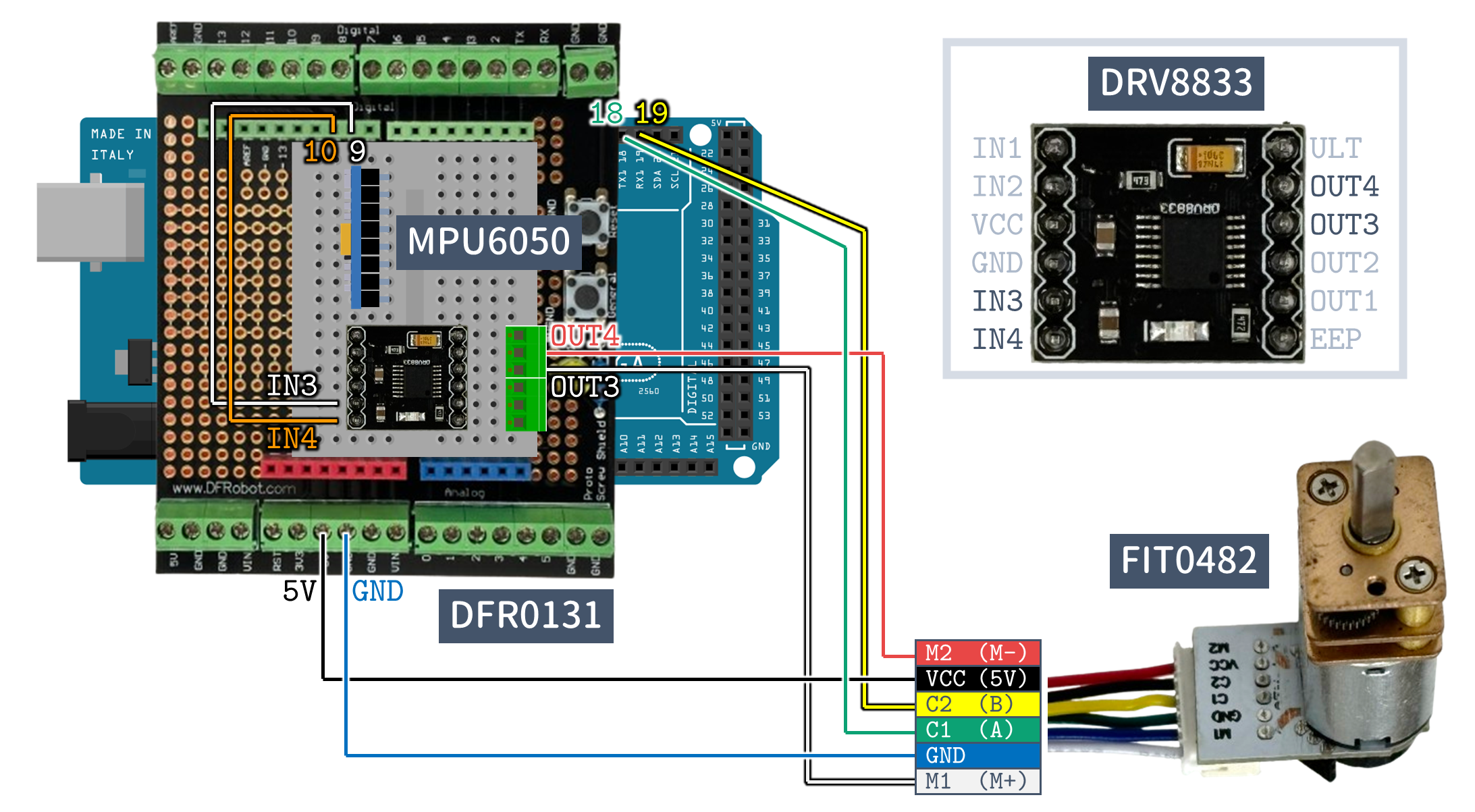
5.1.3 マイコンの配線と LEGO 部品への取り付け
Arduino Mega にプロトタイプ開発用シールドを装着し，その上に，ミニブレッドボードを両面テープで取り付けます．
つぎに，ジャンパワイヤなどを併用して，下図のように接続します．
最後に，下図のように，両面テープでマイコンをボディ上部の LEGO 部品に固定します．
5.1.4 電池ボックスの LEGO 部品への取り付け
下図のように，両面テープで電池ボックスをボディに固定します．固定の際，電池の位置が中心線となるように気をつけてください．
また，電池ボックスの電源プラグを Arduino Mega の DC ジャックに挿し込んでください．
5.1.5 完成図
以上で，車輪型倒立振子は完成です！
5.2 相補フィルタの動作を再確認
5.2.1 土台の LEGO 部品リストと組立図
車輪型倒立振子に搭載された 6 軸センサ MPU6050 の動作確認をするために，LEGO 部品で土台を製作してみましょう．
-
LEGO 部品のリストはこちら（PDF ファイル）です．
-
組立図はこちら（PDF ファイル）です．
この組立図をもとに組み立てた本体は，このようになります．
5.2.2 相補フィルタの動作
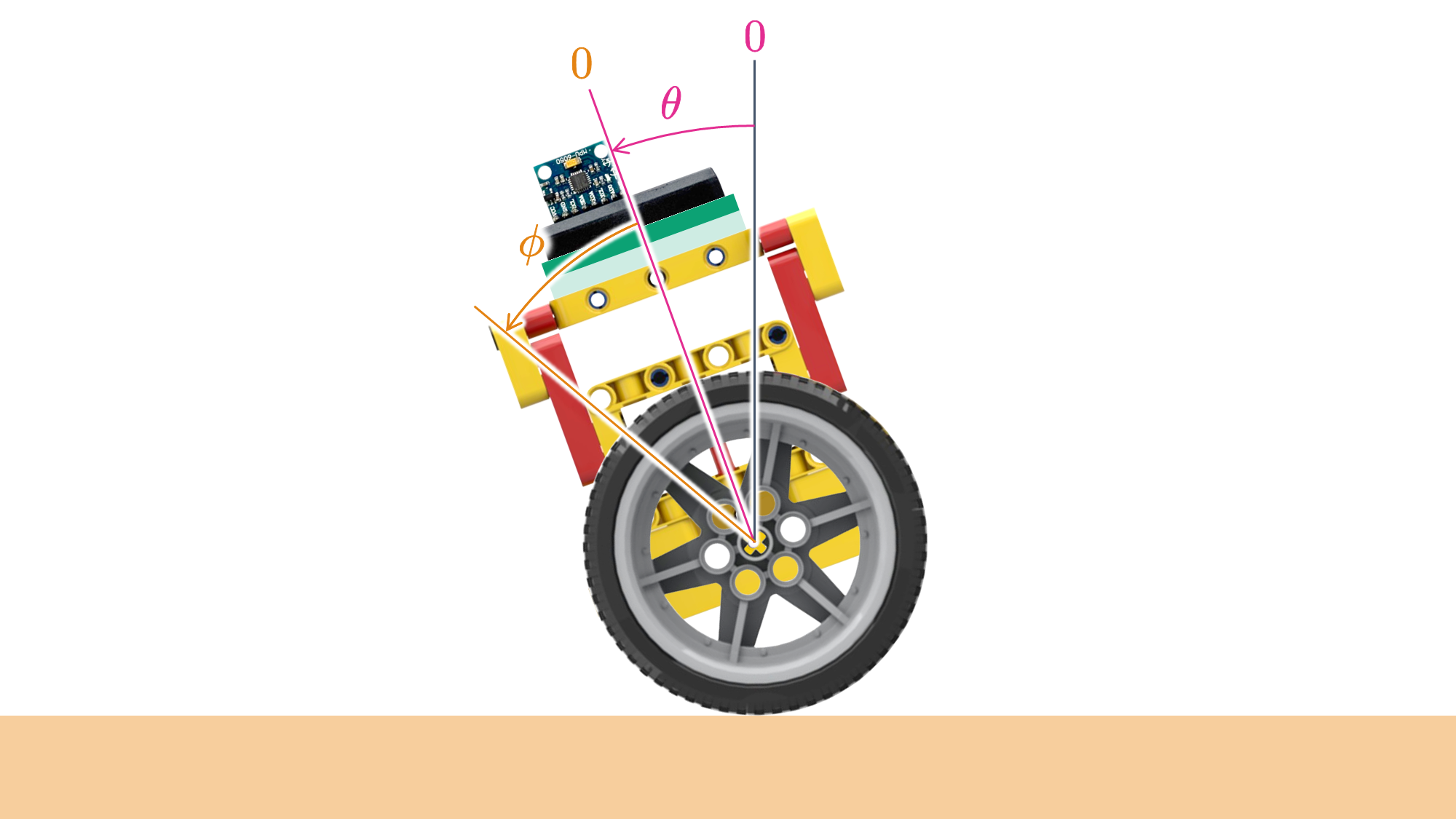
相補フィルタの動作を確認するために，下図に示すように，車輪を取り外した倒立振子のモータ軸を，土台に取り付けます．
このようにすると，モータ後部に取り付けられているロータリエンコーダにより得られる角度がボディ角と等しいため，相補フィルタにより算出されるボディ角の妥当性を検証することができます．
なお，ロータリエンコーダの Simulink での使用方法については，2023 年のアドカレの記事
を参考にしてください．
車輪型倒立振子に搭載した相補フィルタによる角度算出（キャリブレーションあり，初期姿勢が真上で倒立した状態）
まず，先に行ったキャリブレーションによる補正を行います．
>> load data_gyro
>> mean_wx = mean(wx);
>> mean_wy = mean(wy);
>> mean_wz = mean(wz);
>> load data_accel
>> mean_ax = mean(ax);
>> mean_ay = mean(ay);
>> mean_az = mean(az);
そして，車輪型倒立振子を真上で倒立した状態で静止させてから，Simulink モデル $\verb+segway01_sensor.slx+$ を実行してください．
相補フィルタによる角度算出の結果はロータリエンコーダによる角度算出の結果とほぼ同じであり，イイ感じですね！
車輪型倒立振子に搭載した相補フィルタによる角度算出（キャリブレーションあり，初期姿勢が倒れている状態）
つぎに，車輪型倒立振子を倒した状態で静止させてから，Simulink モデル $\verb+segway01_sensor.slx+$ を実行してください．
ロータリエンコーダにより算出される角度は初期姿勢からの相対角です．それに対し，相補フィルタにより算出される角度は真上での倒立状態を基準とした絶対角です．そのため，初期姿勢の影響を受けず，イイ感じですね！
5.3 いよいよ、車輪型倒立振子の安定化
5.3.1 安定化コントローラの形式
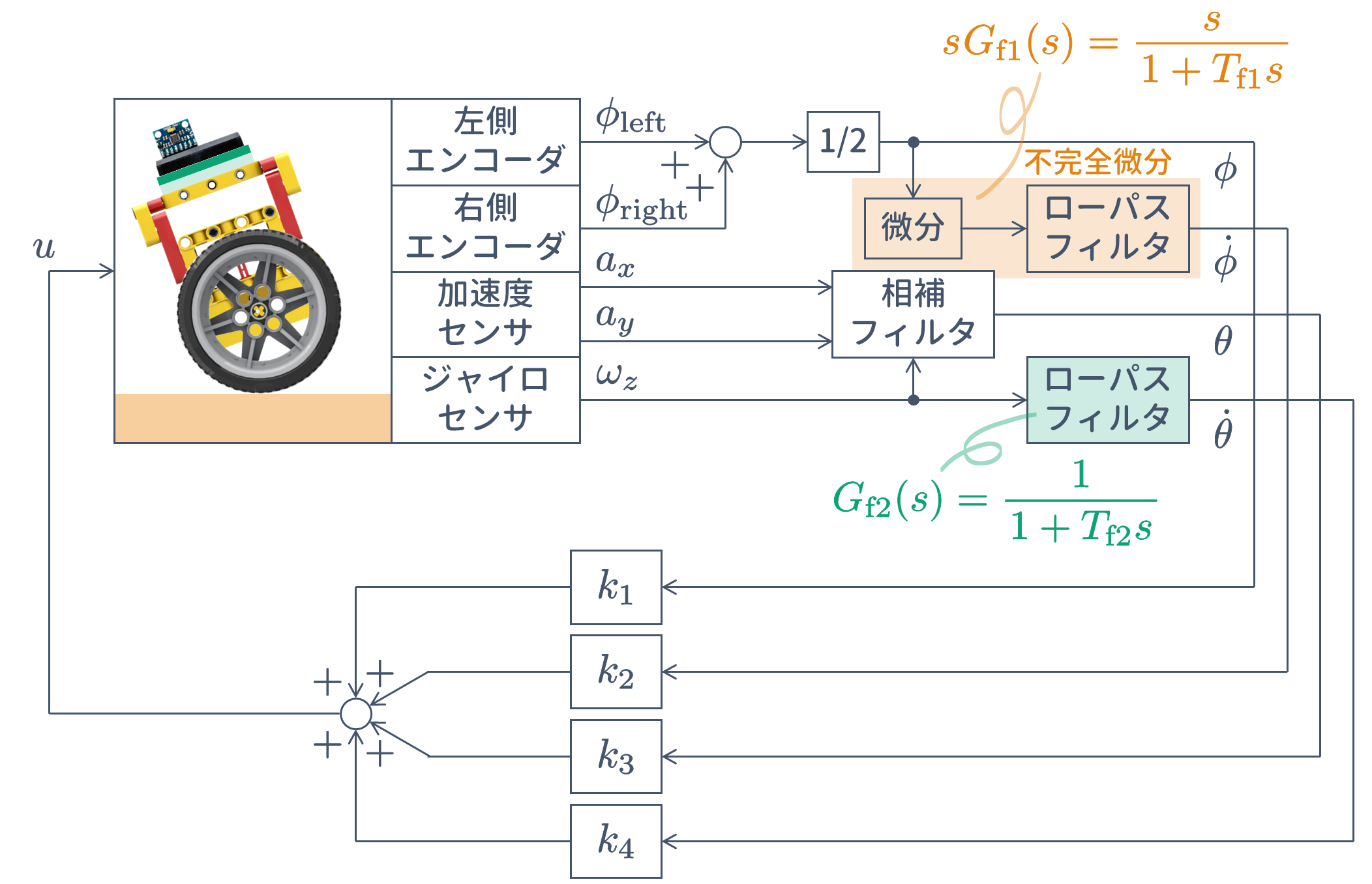
車輪型倒立振子の安定化を行うために
状態フィードバック形式のコントローラ
\begin{align}
u = {k}_{1}\phi
+ {k}_{2}\dot{\phi}
+ {k}_{3}\theta
+ {k}_{4}\dot{\theta}
\tag{5}
\end{align}
を用います．ここで，各状態は以下のとおりです．
-
$\pmb{\phi}$：左右の車輪角の平均であり，左右のモータに取り付けられているロータリエンコーダにより算出します．
-
$\pmb{\dot{\phi} = {\rm d}\phi/{\rm d}t}$：左右の車輪角速度の平均であり，車輪角 $\pmb{\phi}$ を不完全微分（積分器＋ローパスフィルタ $\pmb{s{\hskip1pt}G_{\rm f1}(s) = s/(1 + T_{\rm f1}s)}$ に通過させたもの）を使用します．
-
$\pmb{\theta}$：ボディ角であり，相補フィルタにより算出します．
-
$\pmb{\dot{\theta} = {\rm d}\theta/{\rm d}t}$：ボディ角速度であり，ジャイロセンサにより得られる $\pmb{\omega_z}$ をローパスフィルタ $\pmb{G_{\rm f2}(s) = 1/(1 + T_{\rm f2}s)}$ に通過させたものを使用します．
また，$\pmb{k_1,\ k_2,\ k_3,\ k_4}$ は設計者が値を決定するコントローラゲインです．
制御屋さんであれば，
- ラグランジュ法などにより車輪型倒立振子の数理モデルを導出
- 数理モデルに含まれるパラメータを実験データから決定
- 数理モデルを線形化して，状態方程式を導出
- 最適レギュレータや極配置法などによりコントローラゲインを設計
というアプローチをとるでしょうが，ここでは，手動調整によりコントローラゲインを決定します．
5.3.2 コントローラゲインを手動調整！
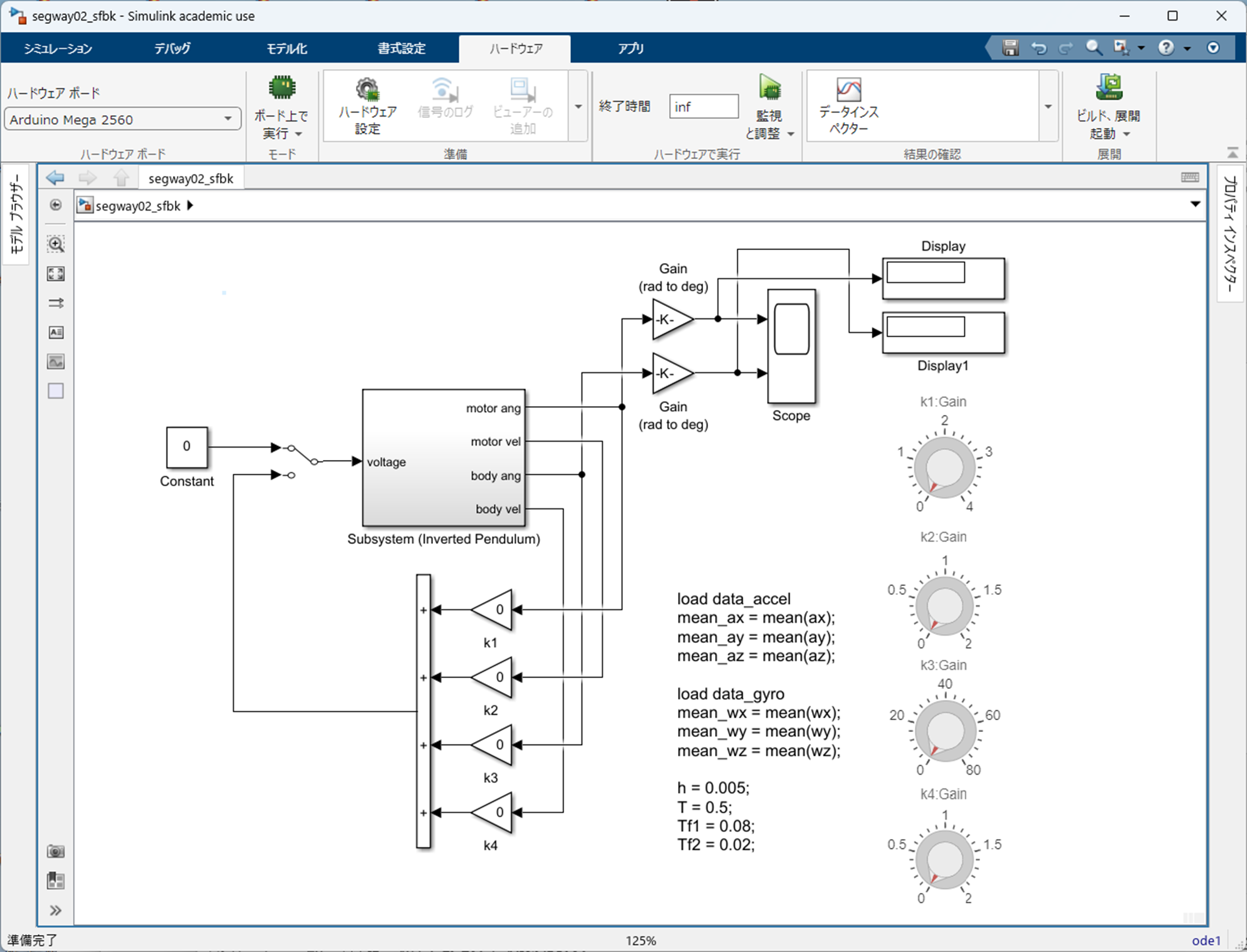
使用する Simulink モデル
- $\verb+segway02_sfbk.slx+$
を下図に示します．
$\verb+Subsystem (Inverted Pendulum)+$ のなかに記述されている $\verb+Subsystem (body)+$ では，下図のように，相補フィルタによるボディ角 $\theta$ を，加えて，ジャイロセンサとローパスフィルタを利用してボディ角速度 $\dot{\theta} = {\rm d}\theta/{\rm d}t$ を算出しています．
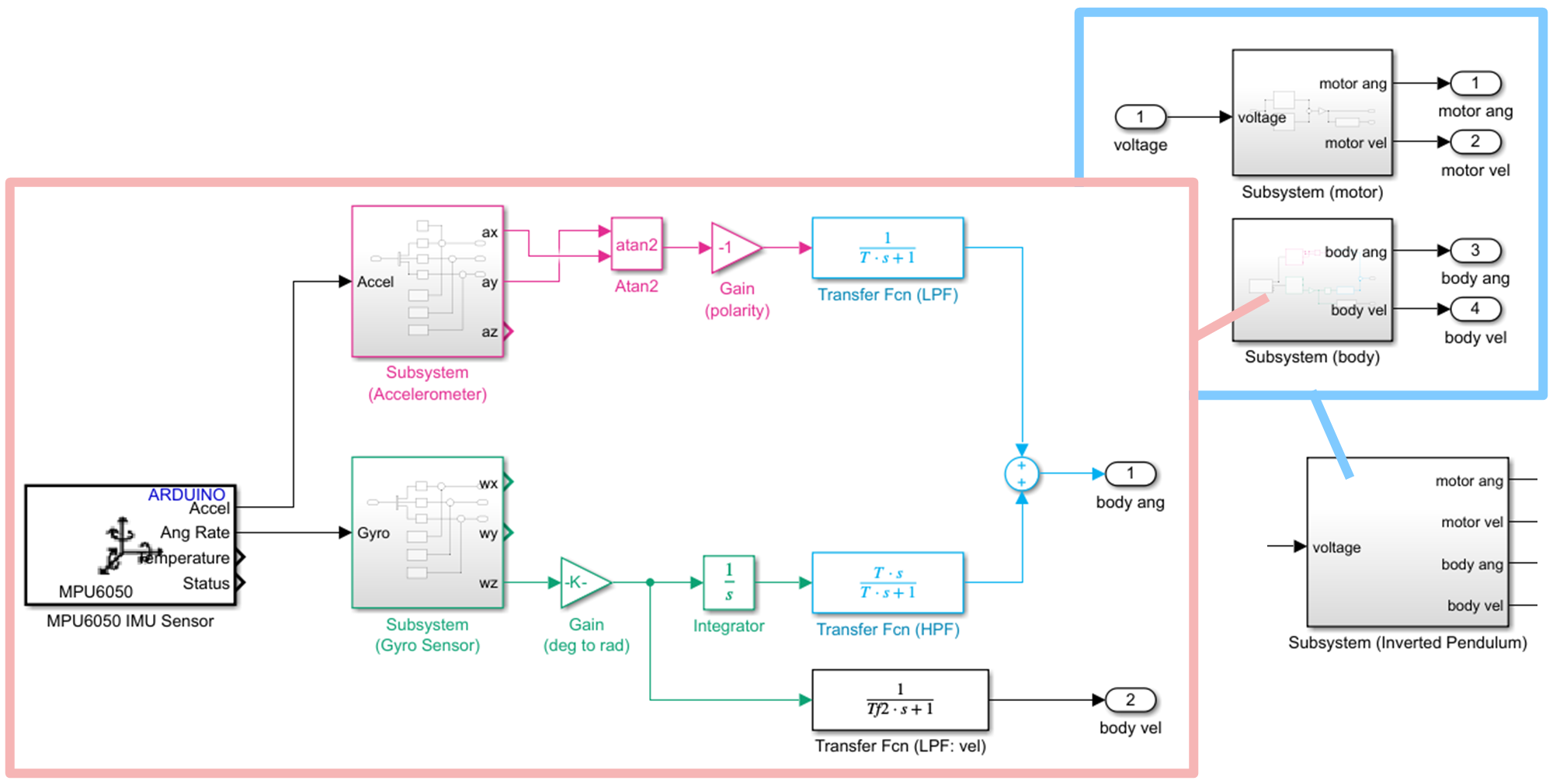
$\verb+Subsystem (Inverted Pendulum)+$ のなかに記述されている $\verb+Subsystem (motor)+$ では，下図のように，エンコーダ用の Simulink ブロック ${\tt Encoder}$ を利用して車輪角 $\phi$ を，さらに，不完全微分により車輪角速度 $\dot{\phi} = {\rm d}\phi/{\rm d}t$ を算出しています．また，Simulink ブロック ${\tt PWM}$ を利用して「正転 / 逆転 / ブレーキ」によりモータを駆動しています．
なお，DC モータ / モータドライバの Simulink での取り扱い方法については，2023 年のアドカレの記事
-
https://qiita.com/Carter/items/5526a72d05f90d073377
- 5.4.3 正負の指令電圧により回転方向と速さを切り替える！
- 5.4.4 モータ角の比例制御を行ってみる！
を参考にしてください．
それでは，以下の手順で，車輪型倒立振子を安定化するコントローラゲインを手動で調整してみてください．
ステップ 1
コマンドウィンドウで
>> load data_accel
>> mean_ax = mean(ax);
>> mean_ay = mean(ay);
>> mean_az = mean(az);
>> load data_gyro
>> mean_wx = mean(wx);
>> mean_wy = mean(wy);
>> mean_wz = mean(wz);
>> h = 0.005; % サンプリング周期
>> T = 0.5; % 相補フィルタの時定数
>> Tf1 = 0.08; % 車輪角速度に対するローパスフィルタの時定数
>> Tf2 = 0.02; % ボディ角速度に対するローパスフィルタの時定数
と入力し，初期設定を行います．そして，Simulink モデル
- $\verb+segway02_sfbk.slx+$
を実行します．
ステップ 2
ステップ 3
ステップ 4
ステップ 5
ステップ 6
ステップ 7
ステップ 8
通し動画はこちらからどうぞ！
なお，最終的に調整されたコントローラゲインは
\begin{align}
k_1 &= 2.2 \\
k_2 &= 0.77 \\
k_3 &= 53.2 \\
k_4 &= 0.96
\end{align}
です．
5.3.3 スタンドアロンで動作させる！
ここまでは，Simulink ブロック $\tt Scope$ による動作確認やパラメータ調整を行うため，エクスターナルモードで Simulink を動かしていました．ここでは，最終的に得られたコントローラゲインを使用して，スタンドアロンで車輪型倒立振子を単独で動かします．
| エクスターナルモード | スタンドアロンモード | |
|---|---|---|
| 動作環境 | Simulink と USB 通信 | Arduino 単独で動作 |
| リアルタイム通信 | USB 経由で可能 | 不可能 |
| 用途 | モニタリング，デバッグ | 実運用 |
| パラメータ調整 | Simulink 上でリアルタイム調整可能 | 実行前に設定する必要あり |
| 効率性 | USB 通信のオーバーヘッドあり | 高い |
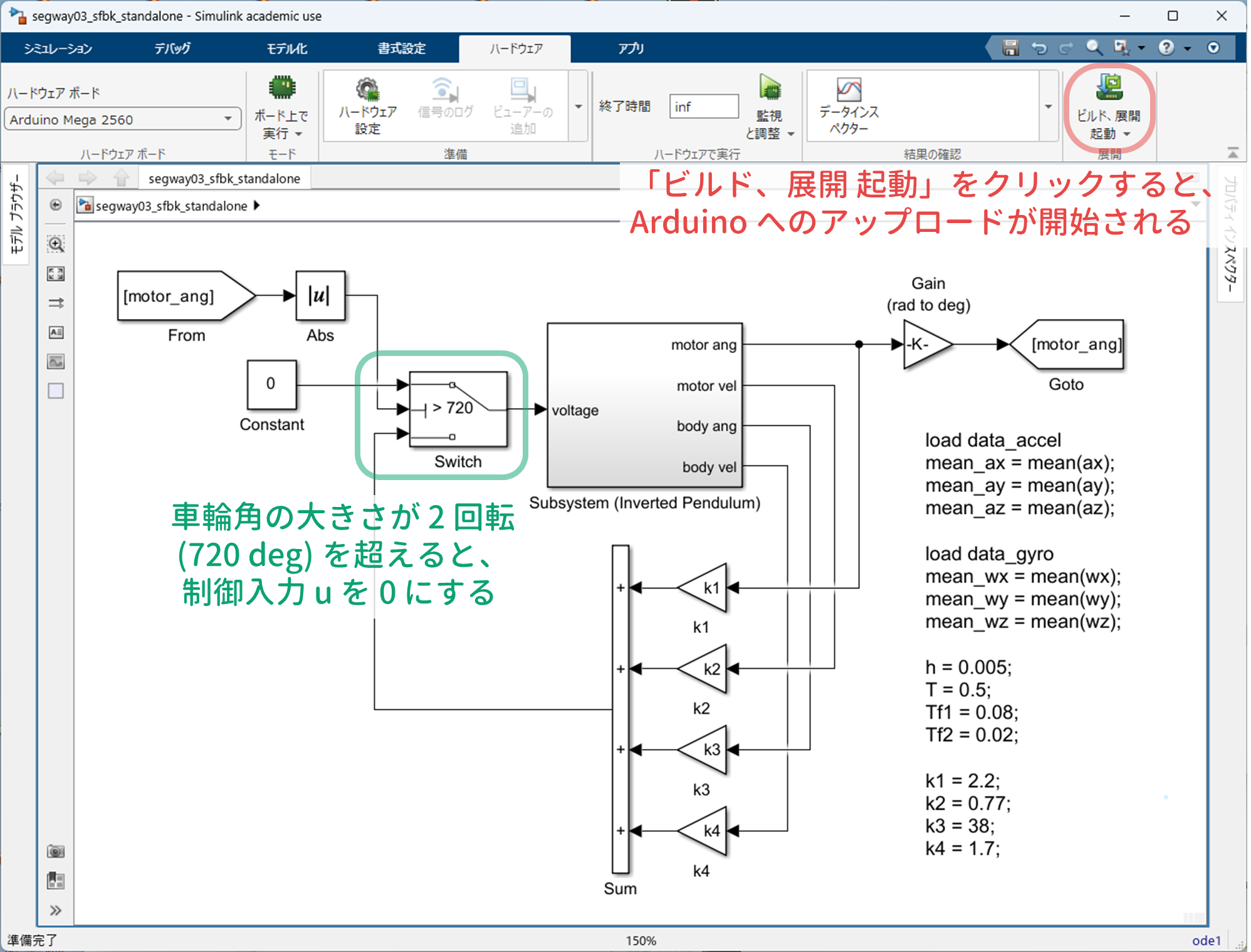
スタンドアロンで動かすための Simulink モデルは
- $\verb+segway03_sfbk_standalone.slx+$
です．モニタリングは不要ですので，Simulink ブロックは削除しています．また，車輪角が $|\phi| > 720\ {\rm [deg]}$ となると，暴走しているとして，制御入力 $u$ 強制的に 0 にします．
以下に，実行の手順を示します．
ステップ 1
コマンドウィンドウで
>> load data_accel
>> mean_ax = mean(ax);
>> mean_ay = mean(ay);
>> mean_az = mean(az);
>> load data_gyro
>> mean_wx = mean(wx);
>> mean_wy = mean(wy);
>> mean_wz = mean(wz);
>> h = 0.005; % サンプリング周期
>> T = 0.5; % 相補フィルタの時定数
>> Tf1 = 0.08; % 車輪角速度に対するローパスフィルタの時定数
>> Tf2 = 0.02; % ボディ角速度に対するローパスフィルタの時定数
>> k1 = 2.2;
>> k2 = 0.77;
>> k3 = 38;
>> k4 = 1.7;
と入力し，初期設定を行います．そして，
- 電源ボックスのスイッチを OFF にする
- 車輪を床面から離している
であることを確認して Simulink モデル
- $\verb+segway03_sfbk_standalone.slx+$
を実行します．コンパイルが終了して，Arduino Mega への転送が終わると，USB からの電源供給により車輪が 2 回転して静止します．
ステップ 2
電源ボックスのスイッチを ON にし，車輪型倒立振子を倒立点付近で軽く支えておきます．そして，Arduino Mega のリセットボタンを押して離すと，安定化制御が開始されます．
5.4 注意したいこと
ネット界隈を見ると，イチケンさんの動画も含め，ボディ角 $\theta$ の制御を目指して，PID コントローラ
\begin{align}
u = {k}_{\rm P}\theta
+ {k}_{\rm I}\int_0^t \theta\,{\rm d}t
+ {k}_{\rm D}\dot{\theta}
\end{align}
を使用している例が多く見られます．しかし，以下のような理由で，個人的にはあまりオススメしません．
-
そもそも車輪角 $\phi$ を制御していないので，どの位置で静止するかはわかりません．そもそも，エンコーダが付属していないモータを利用している場合にこの PID コントローラを利用している傾向が見られます．
-
倒立姿勢で静止している状況を考えると，理想的にはボディ角 $\theta$ は 0 ですが，実際には（わずかかもしれませんが）0 からズレています．そうすると，積分項が増加してしまいます．このことに対処するために，ゴネゴネと補正をする必要があったりして…
6. おわりに
ということで，今年もなんとか投稿を終えました．
私は決してモノづくりが得意なわけではないのですが，そんな私でも，LEGO 部品と汎用のマイコン（Arduino），センサ，モータを利用すれば，いろいろな実験装置が製作できる！ しかも Simulink で簡単に実験ができる！ 「制御工学」の分野を学ぶのであれば，仮想世界に留まらず，実世界に足を踏み入れてみませんか？
この記事が少しでも皆さんのお役に立てば幸いです．
参考文献
-
熊谷：第4 章加速度センサ，角速度センサの活用事例「車輪移動型倒立振子の開発にみるセンサの使い方」，Design Wave Magazine (CQ 出版社)，No. 117, pp. 94-105 (2007)
-
熊谷：倒立振子のパラメータ調整