#追記
2019年7月号のトランジスタ技術に本記事の内容がより詳細に記述されていますので、これから本記事を読もうという方はそちらをご覧になったほうがいいと思います(当然ですが、トラ技の執筆者は私ではありません)。
概要
倒立振子とは
倒立振子はまさにその字が表わすように,通常の振子とは逆向きな振子です.通常の振子は一度手を離すと,最終的には最下端で収束し,静止します.しかし倒立振子は,通常の振子とは異なり,わずかな外乱によって,発散(転倒)してしまいます.よって倒立状態を維持するためには適切な制御が必要となります.そのように,不安定な系であるため制御工学の題材として用いられることが多くなっております.
倒立振子は大まかに何種類かに分類されます.
- 台車型倒立振子
もっとも広く実験に用いられるタイプの振子です.左右に動く台車の上に自由に動く振子が取り付けられたものです. - 回転型倒立振子
水平面状を回転するアームの先端に振子が取り付けられたものです.発案者の名前からFuruta Pendulumとも呼ばれるそうです.参考文献を読んでいて初めてその存在を知りました. - アーム型倒立振子
円直面を回転するアームの先端に振子が取り付けられたものです.Pendubotで検索すると非常に多くの例が出てきます.台車型や回転型よりも制御が困難であるらしいです.しかし,実際にデモとして最も多く用いられている用に感じます.いつかは挑戦してみたいタイプです. - 車輪型倒立振子
まさにセグウェイが,このタイプとなります.今回はこのタイプの倒立振子について実際に制御を行いたいました. - その他
その他にも慣性ロータを用いたもの(ムラタセイサク君?)であったり,振子を2重,3重に拡張したものもあります.
今回は,車輪型の倒立振子を対象としました.
さて,倒立振子に関わらず,制御工学では一部を除くと,基本的には制御対象のモデルが必要となります.底で、通常は運動方程式やら何やらから,制御対象のモデルを構築したり,システム同定によって対象のモデルを得たりします.
ネット上の多くの倒立振子では,そのパラメタは試行錯誤的な調整で決められているものが多いようです.一方で,各種の論文となると全てのパラメタが完全に分かるような実験機器(それなりに高価)なものを使用しているようです.
今回は,制御工学を実機に適用しようという目的の元で,やはり対象のモデルを得たうえで,制御器を設計したいと考えました.しかし,高価な装置を買うのも大変です.そこで,簡易に測定可能なパラメタ(重量やタイヤ半径等)は実際に測定し,測定の難しいパラメタ(慣性モーメントや粘性係数等)をシステム同定によって得ることに挑戦しました.
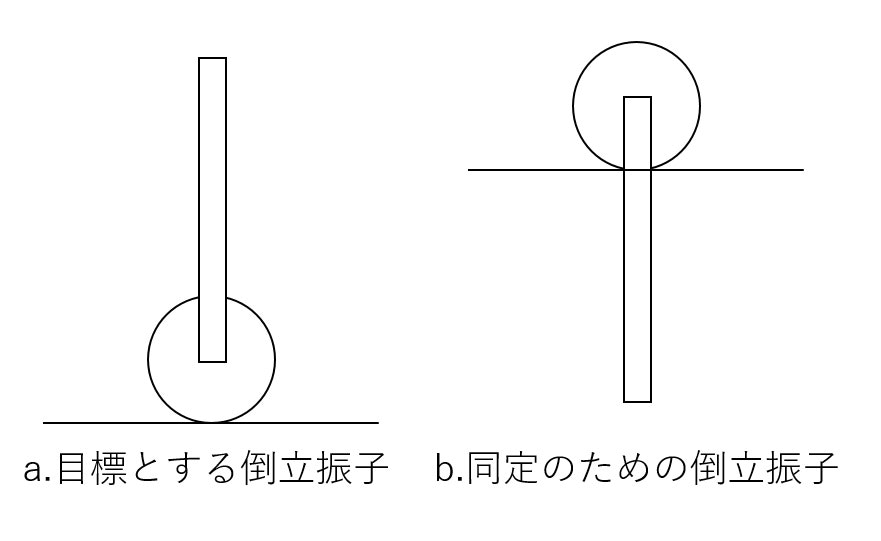
一般に,対象システムが安定であれば同定実験を行うことは非常に容易です.しかし,倒立振子は不安定です(a).そこで,今回は図(b)のように車輪型倒立振子を180度反転させた状態で同定実験を行い,必要なパラメタの同定を行いました.
図1 概要
また,倒立振子は厳密には非線形なモデルです.しかし,非線形制御は非常に複雑となるため,倒立状態の近傍で線形化したモデルを用います.また,同定実験に用いる振子モデルも同様に最下端近傍で線形化を行いました.
今回の記事で行ったことの流れはおおよそ次のとおりです.
- 倒立振子モデルの設定及び$\theta=0,\pi$での近似
- $\theta=\pi$での同定実験及び同定
- LQRによる状態フィードバックゲインの算出
- 実機実験
使用装置
今回は図のように車輪型倒立振子を製作しました.ハードウェアの詳細については表のとおりです.
図2 実機
表1 主な使用部品
| 呼称 | 仕様 |
|---|---|
| モータ(エンコーダ付き) | 1524 G0722(定格 12V 512pulse/r) |
| MCU | RX631(R5F5631FDDFP) |
| 加速度・ジャイロセンサ | MPU6050モジュール(Amazon) |
| モータドライバ | DRV8835 |
| 電源 | エネループ8本 |
実際に用いた基板を図に示す.
図3 モータドライバ基板
倒立振子モデルから状態方程式の導出
倒立振子のモデル化
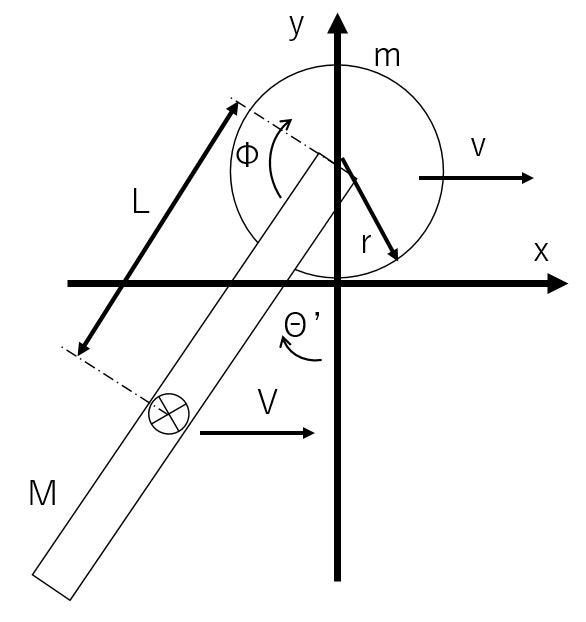
まず,倒立振子をモデル化するために,必要な変数の設定や,各種定数を図のようにとりました.
図4 倒立振子モデル
定数については,一括で示しました.この時に簡易に測定が行えた定数は数値を,同定する必要のある定数はNaNとして,表記しました.
表2 定数の定義
| 定数名 | 数値 | 説明 |
|---|---|---|
| I | NaN | ボディーの慣性モーメント[$kg m^2$] |
| J | NaN | 車輪の慣性モーメント[$kg m^2$] |
| $D_{\phi}$ | NaN | 車輪の粘性摩擦係数[$kg m^2/s$] |
| $D_{\theta}$ | NaN | 本体の粘性摩擦係数[$kg m^2/s$] |
| $K_T$ | NaN | モータのトルク定数[Nm/A] |
| $K_E$ | NaN | モータの逆起電力定数[V/(rad/s)] |
| $R_a$ | NaN | モータの内部抵抗[$\Omega$] |
| $J_m$ | NaN | モータ部の慣性モーメント[$kg m^2$] |
| M | 0.641 | 本体の質量[kg] |
| m | 0.0485 | 車輪の合計質量[kg] |
| L | 0.065 | 車軸から本体部重心への距離[m] |
| r | 0.0575/2 | 車輪の半径[m] |
| g | 9.8192 | 重力加速度[$m/s^2$] |
| n | 19 * (50/12):1 | 減速比 |
また変数については次のように設定した.
表3 変数の定義
| 変数名 | 内容 |
|---|---|
| v | 車輪の速度[m/s] |
| V | 本体の速度[m/s] |
| $\theta$ | 座標軸から本体の傾き[rad] |
| $\phi$ | 車輪の回転角度[rad] |
倒立振子の運動方程式
今回はラグランジェの運動方程式を用います.これについてはいまいち理解が浅いので,分かりやすい文献等ありましたらコメントいただけたらと思います.
まずラグランジェの運動方程式は,次式である.
$$
\frac{d}{dt}(\frac{\partial T}{\partial \dot{q_i}})-\frac{\partial T}{\partial q_i}+\frac{\partial U}{\partial q_i}+\frac{\partial F}{\partial \dot{q_i}}=\tau_i
$$
ここで,Tは全体の運動エネルギー,Uは位置エネルギー,Fは散逸エネルギーである.
各項についてそれぞれ求めていく.
まず,車輪の回転運動エネルギーについてはT_{wr},次式である.
$$
T_{wr}=\frac{1}{2}J( \dot{\phi}+\dot{\theta})^2
$$
胴体の傾斜方向の回転運動エネルギーT_{Br}は,
$$
T_{Br}=\frac{1}{2}I\dot{\theta}^2
$$
車輪の並進運動エネルギーについて求める.まず,車輪の動く速さは,
$$
v=r(\dot{\phi}+\dot{\theta})
$$
となる.よって,車輪の並進運動エネルギーは,
$$
T_{wh}=\frac{1}{2}mv^2=\frac{1}{2}mr^2(\dot{\theta}^2+2\dot{\theta}\dot{\phi}+\dot{\phi}^2)
$$
である.
本体の並進運動エネルギーについて求める.まずタイヤの回転中心は,
\begin{align}
x_c&=r(\theta + \phi)\\
y_c&=r
\end{align}
また,本体重心座標は,
\begin{align}
x_p&=x_c + Lsin\theta\\
y_p&=y_c + Lcos\theta
\end{align}
以上から,本体の重心速度は,
\begin{align}
V_x&=\frac{d}{dt}x_p=r(\dot{\theta}+\dot{\phi})+L\dot{\theta}(cos\theta - sin\theta)\\
V_y&=\frac{d}{dt}y_p=0
\end{align}
よって,本体の並進運動エネルギーは,
\begin{align}
T_{Bt}&=\frac{1}{2}MV^2=\frac{1}{2}M(V_x^2+V_y^2)\\
&=\frac{1}{2}M(\dot{\phi}^2r^2+\dot{\theta}^2(r^2+2rLcos\theta+L^2)+2\dot{\phi}\dot{\theta}(r^2+rLcos\theta))
\end{align}
これまで求めた各部の運動エネルギーの和が全体の運動エネルギーとなるので,
\begin{align}
T&=T_{wr}+T_{Br}+T_{wt}+T_{Bt}\\
&=\frac{1}{2}J( \dot{\phi}+\dot{\theta})^2+\frac{1}{2}I\dot{\theta}^2+\frac{1}{2}mv^2+\frac{1}{2}mr^2(\dot{\theta}^2+2\dot{\theta}\dot{\phi}+\dot{\phi}^2)+\frac{1}{2}M(\dot{\phi}^2r^2+\dot{\theta}^2(r^2+2rLcos\theta+L^2)+2\dot{\phi}\dot{\theta}(r^2+rLcos\theta))
\end{align}
である.
また,位置エネルギーは重心位置のEだけを考えればよいので,
\begin{align}
U&=Mgy_p\\
&=Mg(r+Lcos\theta)
\end{align}
最後に,散逸エネルギーについては,車輪・車軸周りの摩擦を考慮すればよいので,
$$
F=\frac{1}{2}D_{\phi}\dot{\phi}^2+\frac{1}{2}D_{\theta}\dot{\theta}^2
$$
となる.
以上から,ラグランジュの運動方程式を
\begin{align}
q_1&=\theta\\
q_2&=\phi
\end{align}
として利用する.
以下で各項について記したので,必要があれば利用いただきたい.
\begin{align}
\frac{d}{dt}(\frac{\partial T}{\partial \dot{\theta}})
&=\frac{d}{dt}( (J+mr^2+MrLcos\theta)\dot{\phi} + (J+mr^2+Mr^2+I+2MrLcos\theta+ML^2)\dot{\theta} )\\
&=(J+Mr^2+mr^2+MrLcos\theta)\ddot{\phi}-MrL\dot{\theta}\dot{\phi}sin\theta+(J+mr^2+Mr^2+I+2MrLcos\theta+ML^2)\ddot{\theta}-2MrL\dot{\theta}^2cos\theta
\end{align}
\begin{align}
\frac{d}{dt}(\frac{\partial T}{\partial \dot{\phi}})
&=\frac{d}{dt}( (J+mr^2+Mr^2)\dot{\phi}+(J+mr^2+Mr^2+MrLcos\theta)\dot{\theta} )\\
&=(J+mr^2+Mr^2)\ddot{\phi}+(J+mr^2+Mr^2+MrLcos\theta)\ddot{\theta}-MrL\dot{\theta}^2sin\theta
\end{align}
$$ \frac{\partial T}{\partial \theta} =-MrL\dot{\theta}^2sin\theta-MrL\dot{\phi}\dot{\theta}sin\theta $$ $$ \frac{\partial T}{\partial \phi} =0 $$ $$ \frac{\partial U}{\partial \theta} =-MgLsin\theta $$ $$ \frac{\partial U}{\partial \phi}=0 $$ $$ \frac{\partial F}{\partial \dot{\theta}}=D_\theta\dot{\theta} $$ $$ \frac{\partial F}{\partial \dot{\phi}}=D_\phi\dot{\phi} $$ 以上がラグランジェの各項である.
ラグランジェの運動方程式は,
\begin{align}
\frac{d}{dt}(\frac{\partial T}{\partial \dot{\theta}})-\frac{\partial T}{\partial \theta}+\frac{\partial U}{\partial \theta}+\frac{\partial F}{\partial \dot{\theta}}=0\\
\frac{d}{dt}(\frac{\partial T}{\partial \dot{\phi}})-\frac{\partial T}{\partial \phi}+\frac{\partial U}{\partial \phi}+\frac{\partial F}{\partial \dot{\phi}}=\tau
\end{align}
である.
よって,各項を代入すると,
\begin{align}
0&=(J+Mr^2+mr^2+MrLcos\theta)\ddot{\phi}-MrL\dot{\theta}\dot{\phi}sin\theta+(J+mr^2+Mr^2+I+2MrLcos\theta+ML^2)\ddot{\theta}-2MrL\dot{\theta}^2cos\theta+MrL\dot{\theta}^2sin\theta +MrL\dot{\phi}\dot{\theta}sin\theta-MgLsin\theta+D_{\theta}\dot{\theta} \\
\tau&=(J+mr^2+Mr^2)\ddot{\phi}+D_{\phi}\dot{\phi}+(J+mr^2+Mr^2+MrLcos\theta)\ddot{\theta}-MrL\dot{\theta}^2sin\theta
\end{align}
ここで,
\begin{align}
a&=(m+M)r^2+J\\
b&=MrL\\
c&=Ml^2+I\\
d&=MgL
\end{align}
とすると,
\begin{align}
0&=(a+bcos\theta)\ddot{\phi}+(a+c+2bcos\theta)\ddot{\theta}+(bsin\theta-2bcos\theta)\dot{\theta}^2-dsin\theta+D_{\theta}\dot{\theta} \\
\tau&=a\ddot{\phi}+D_{\phi}\dot{\phi}+(a+bcos\theta)\ddot{\theta}-mrL\dot{\theta}^2sin\theta
\end{align}
となる.
以上が,倒立振子に関する運動方程式となる.
0近傍での近似式
前銃の運動方程式は非線形なものであるため,制御工学的には非常に扱いが難しい.そこで,$\theta=0$の近傍で線形化を行う.$\theta$に関して,
\begin{align}
cos\theta \simeq1\\
sin\theta\simeq\theta\\
\dot{\theta}^2\simeq0
\end{align}
と近似される.
よって,
\begin{align}
0&=(a+b)\ddot{\phi}+(a+c+2b)\ddot{\theta}-d\theta+D_{\theta}\dot{\theta}\\
\tau&=a\ddot{\phi}+(a+b)\ddot{\theta}+D_{\phi}\dot{\phi}
\end{align}
と$\theta=0$近傍では近似される.
次に,モータ部の特性を考慮し,モデル化を行う.
まず,モータの発生するトルクとの関係から,
$$
J_m\ddot{\phi_A}=\tau_A-\frac{\tau}{n}
$$
よって,前述した近似式を代入し,
$$
J_m\ddot{\phi_A}=\tau_A-\frac{a\ddot{\phi}+(a+b)\ddot{\theta}+D_{\phi}\dot{\phi}}{n}
$$
となる.また,
$$
n=\frac{\phi_A}{\phi}
$$
より,
$$
n\tau_A=J_mn^2\ddot{\phi}+a\ddot{\phi}+(a+b)\ddot{\theta}+D_{\phi}\dot{\phi}
$$
となる.
一方で,モータ部の電気回路を考えると,インダクタンスが十分に小さい時には,
\begin{align}
V_E=R_ai+K_E\dot{\phi}\\
\therefore i=\frac{V_E-K_En\dot{\phi}}{R_a}\\
\end{align}
よって,発生トルクは,
\begin{align}
\tau_A&=K_Ti\\
&=K_T\frac{V_E-K_En\dot{\phi}}{R_a}
\end{align}
となる.よって,$n\tau_A=$の式に代入すると,
$$
(a+J_mn^2)\ddot{\phi}+(a+b)\ddot{\theta}+(D_{\phi}+\frac{K_T K_E}{R_a}n^2)\dot{\phi}=\frac{nK_T}{R_a}V_E
$$
となる.
ここで,
\begin{align}
E&=a+J_mn^2\\
F&=a+b\\
G&=D_{\phi}+\frac{K_T K_E}{R_a}n^2\\
H&=a+2b+c
\end{align}
とすると,前述までの2つの近似式は,
\begin{align}
E\ddot{\phi}+F\ddot{\theta}+G\dot{\phi}=\frac{K_Tn}{R_a}V_E\\
F\ddot{\phi}+H\ddot{\theta}-d\theta+D_{\theta}\dot{\theta}=0
\end{align}
となる.
制御のためには状態空間表現としたいので,状態量xを
$$
x^T=[\theta, \dot{\theta}, \dot{\phi}]
$$
と設定する.また,入力をモータ電圧V_Eとする.すると,近似式を\ddot{\phi},\ddot{\theta}について解くことで,用意に次の状態方程式は,
\begin{align}
\dot{x}=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
-\frac{Ed}{F^2-EH} & \frac{ED_{\theta}}{F^2-EH} & -\frac{FG}{F^2-EH} \\
\frac{Fd}{F^2-EH} & \frac{FD_{\theta}}{F^2-EH} & \frac{GH}{F^2-EH}
\end{array}
\right)x+\left(
\begin{array}{c}
0 \\
\frac{FK_Tn}{R_a(F^2-EH)} \\
-\frac{HK_Tn}{R_a(F^2-EH)}
\end{array}
\right)V_E
\end{align}
以上が,$\theta=0$近傍での状態方程式となる.LQRを適用する際には本式を利用する.
π近傍での近似式
同定のために$\theta = \pi$近傍で用いるモデルを導出する.座標系のうち$\theta$の原点を図のように変更すると,
図5 倒立振子の反転モデル
\begin{align}
x_c&=r(\theta'+\phi)\\
y_c&=r
\end{align}
また,
\begin{align}
x_p&=x_c-Lsin\theta'\\
y_p&=y_c-Lcos\theta'
\end{align}
以上から,
\begin{align}
V_x&=\frac{d}{dt}x_p=r(\dot{\theta'}+\dot{\phi})-\dot{\theta'}Lcos\theta'\\\
V_y&=\frac{d}{dt}y_p=L\dot{\theta'}sin\theta'
\end{align}
よって,以上から,$\theta=0$のときと同様に計算すると,
\begin{align}
0&=(a-b)\ddot{\phi}+(a+c-2b)\ddot{\theta'}-d\theta'+D_{\theta'}\dot{\theta'}\\
\tau&=a\ddot{\phi}+(a-b)\ddot{\theta'}+D_{\phi}\dot{\phi}
\end{align}
となる.この式は\theta=0の場合におけるbの係数をマイナスとしたものであるから,まったく同様の色変形から,その最終的な状態方程式は,
\begin{align}
F'&=a-b\\
H'&=a-2b+c
\end{align}
と置くことによって,容易に次の状態方程式を求めることができる.
\begin{align}
\dot{x}=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
-\frac{Ed}{F'^2-EH'} & \frac{ED_{\theta}}{F'^2-EH'} & -\frac{F'G}{F'^2-EH'} \\
\frac{F'd}{F'^2-EH'} & \frac{F'D_{\theta}}{F'^2-EH'} & \frac{GH'}{F'^2-EH'}
\end{array}
\right)x+\left(
\begin{array}{c}
0 \\
\frac{F'K_Tn}{R_a(F'^2-EH')} \\
-\frac{H'K_Tn}{R_a(F'^2-EH')}
\end{array}
\right)V_E
\end{align}
同定実験
実験条件について
通常,同定実験では,プレ同定の後に詳細な実験条件を設定することが多いが,今回は適切なプレ同定実験を考案できなかったため,実験と同定を繰り返し行い,パラメタの設定を行った.最終的に用いたパラメタは次のとおりである.
表4 同定実験のパラメタ
| パラメタ | 数値 |
|---|---|
| 入力電圧振幅[V] | 2.0 |
| M系列信号周波数[Hz] | 50 |
| データサンプリング周波数[Hz] | 50 |
| 実験時間[sec] | 20 |
このとき,実際に用いた実験環境を図に示す.
図6 同定実験の環境
MATLABによるパラメタの同定
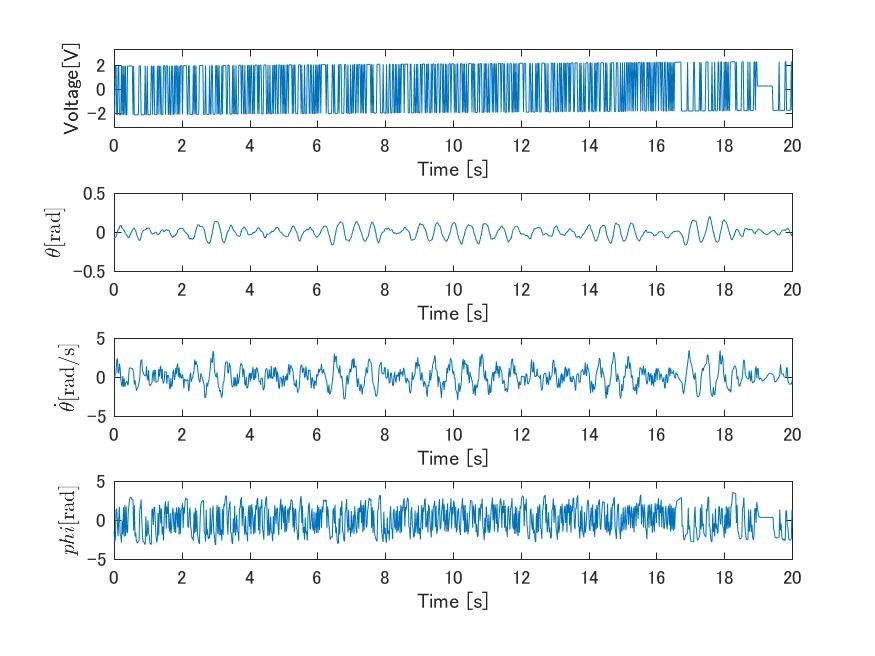
実際に測定したデータを図に示す.
図7 同定実験の結果
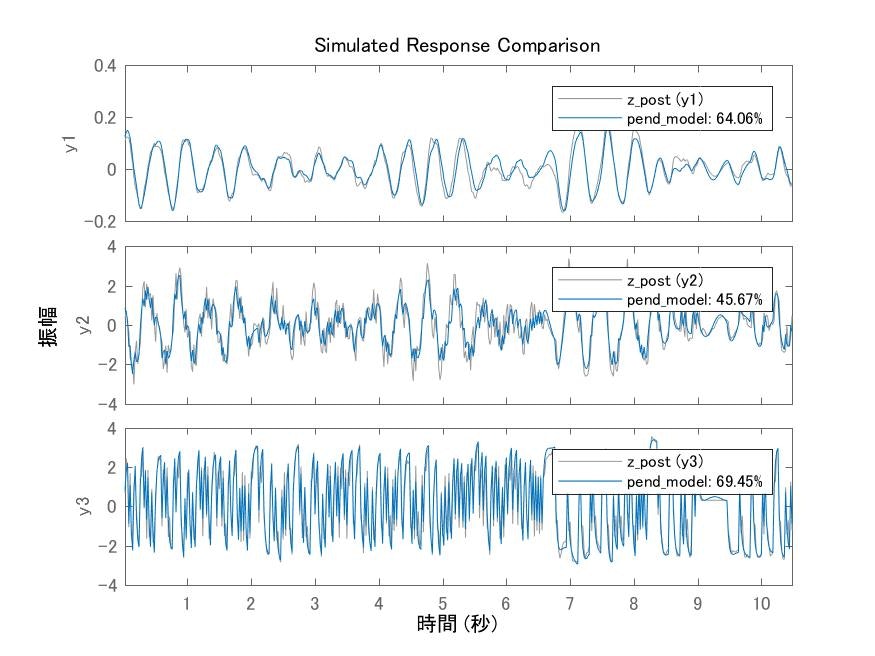
この時のデータを用いてパラメタの同定を行った.$\theta=pi(\theta'=0)$近傍におけるモデルに対して同定を行う必要があったので,そのモデルをpend.mとして用意した.また,この時の同定に用いたスクリプトをid_pend_sim_gray.mとした.詳しい同定の中身については,参考文献や,以前の投稿を参照していただきたい.このときの同定結果を図として示す.
図8 同定結果
表5 pend.m
function [ A,B,C,D,K,X0] = pend( par,ts,aux )
%倒立振子θ=90近傍の状態方程式同定のための関数 for pem()
% 詳細説明をここに記述
% 上から順にpar(1),(2),(3)...
% 同定するべきパラメタ群 par_guess 初期値(予想値)
% I=0.004160; % [kg m^2]本体の慣性モーメント
% J=0.000040; % [kg m^2]車輪の慣性モーメント 0.000020 *2
% D_phi=; % [kg m^2/s]車輪の粘性摩擦係数 この2つに関してはなにも分からない
% D_theta=; % [kg m^2/s]本体の粘性摩擦係数
% Kt = 8.37e-3;%[Nm/A] mNm/A
% Ke = 0.877e-3 *(30 / 3.14);%V/(rad/s)
% Ra = 10.4;
% Jm=0.7e-7;
%既知定数
M=0.641; % [kg]本体の質量
m=0.0485; % [kg]車輪の質量 2つ合わせたもの回転部全部のということ
L=0.065; % [m]車軸から本体部重心への距離
r=0.0575/2; % [m]車輪の半径
g=9.8192; % [m/s^2]重力加速度
n = 19 * (50/12); %減速比
%展開してparであらわさないとならないみたいです.マクロかなんかでもいけるのかな?
A=[0 1 0;
((((m+M)*r*r+par(2)) + par(8) * n * n)*(M*g*L)/((((m+M)*r*r+par(2)) - (M*r*L))*(((m+M)*r*r+par(2)) - (M*r*L)) - (((m+M)*r*r+par(2)) + par(8) * n * n) * (((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1))))) ((((m+M)*r*r+par(2)) + par(8) * n * n)*par(4) / ((((m+M)*r*r+par(2)) - (M*r*L))*(((m+M)*r*r+par(2)) - (M*r*L)) - (((m+M)*r*r+par(2)) + par(8) * n * n)*(((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1))))) (-(((m+M)*r*r+par(2)) - (M*r*L))*(par(3) + (par(5) * par(6) * n * n)/par(7)) / ((((m+M)*r*r+par(2)) - (M*r*L))*(((m+M)*r*r+par(2)) - (M*r*L)) - (((m+M)*r*r+par(2)) + par(8) * n * n)*(((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1)))));
(-(((m+M)*r*r+par(2)) - (M*r*L))*(M*g*L) / ((((m+M)*r*r+par(2)) - (M*r*L))*(((m+M)*r*r+par(2)) - (M*r*L)) - (((m+M)*r*r+par(2)) + par(8) * n * n)*(((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1))))) (-(((m+M)*r*r+par(2)) - (M*r*L)) * par(4) /((((m+M)*r*r+par(2)) - (M*r*L))*(((m+M)*r*r+par(2)) - (M*r*L)) - (((m+M)*r*r+par(2)) + par(8) * n * n)*(((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1))))) ((par(3) + (par(5) * par(6) * n * n)/par(7)) * (((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1))) /((((m+M)*r*r+par(2)) - (M*r*L))*(((m+M)*r*r+par(2)) - (M*r*L)) - (((m+M)*r*r+par(2)) + par(8) * n * n)*(((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1)))))
];
B=[0;
((((m+M)*r*r+par(2)) - (M*r*L))*par(5)*n / (par(7) * ((((m+M)*r*r+par(2)) - (M*r*L))*(((m+M)*r*r+par(2)) - (M*r*L)) - (((m+M)*r*r+par(2)) + par(8) * n * n)*(((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1))))));
(-(((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1)))*par(5)*n / (par(7) * ((((m+M)*r*r+par(2)) - (M*r*L))*(((m+M)*r*r+par(2)) - (M*r*L)) - (((m+M)*r*r+par(2)) + par(8) * n * n)*(((m+M)*r*r+par(2)) - 2*(M*r*L) + (M*M*L+par(1))))))
];
C = [1 0 0;0 1 0;0 0 1];
D = [0; 0 ;0];
K = zeros(3,3);
X0 =[0 ;0 ; 0];
if ts>0 % Sample the model with sample time Ts
s = expm([[A B]*ts; zeros(1,4)]);
A = s(1:3,1:3);
B = s(1:3,4);
end
表6 id_pend_sim_gray.m
clear all;
close all;
format compact;
[numeric , txt] = xlsread('20170918id_logger_data.csv');
t = numeric(:,1);
U0 = numeric(:,5);
Y0a = numeric(:,2); % theta [rad]
Y0a = - Y0a; % theta [rad]
Y0b = numeric(:,3); % theta_dot [rad/s]
Y0b = - Y0b;% theta_dot [rad/s]
Y0c = numeric(:,4) /(19 * (50/12)); % phi_dot [rad/s] 減速比を忘れないように
%無駄部分の除去
%今回は必要なかった
No = min(find(t >=0));
t=t(No:end);
U1=U0(No:end);
Y1a=Y0a(No:end);
Y1b=Y0b(No:end);
Y1c=Y0c(No:end);
% %平均値除去(バイアス除去)
U2=detrend(U1,'constant');
Y2a=detrend(Y1a,'constant');
Y2b=detrend(Y1b,'constant');
Y2c=detrend(Y1c,'constant');
% トレンド除去
U3 = detrend(U2);
Y3a = detrend(Y2a);
Y3b = detrend(Y2b);
Y3c = detrend(Y2c);
%トレンドの消去確認
%除去後の入力データの評価
PU2 = polyfit(t,U3,1); %1次近似式の係数
VU2 = polyval(PU2,t); %1次近似式の値
%除去後の出力データについての評価
PY2a = polyfit(t,Y3a,1);
VY2a = polyval(PY2a,t);
PY2b = polyfit(t,Y3b,1);
VY2b = polyval(PY2b,t);
PY2c = polyfit(t,Y3c,1);
VY2c = polyval(PY2c,t);
% % データを分割します
No2 = find(abs(t - 10.0) <=eps );
% 前半データ
U3_pre = U3(1:No2);
Y3a_pre = Y3a(1:No2);
Y3b_pre = Y3b(1:No2);
Y3c_pre = Y3c(1:No2);
% 後半データ
U3_post = U3(No2:end);
Y3a_post = Y3a(No2:end);
Y3b_post = Y3b(No2:end);
Y3c_post = Y3c(No2:end);
u = U3_pre;
y = [Y3a_pre Y3b_pre Y3c_pre ];
z = iddata(y,u,0.02);
u_post = U3_post;
y_post = [Y3a_post Y3b_post Y3c_post ];
z_post = iddata(y_post,u_post,0.02);
par_guess = [0.004160 0.000040 1.00e-3 1.00e-1 8.37e-3 0.877e-3*(30/3.14) 10.4 0.7e-7];
%par_guessの初期値に同定結果がかなり左右されるようなので調整必要かも
aux=[];
pend_model = idgrey('pend',par_guess,'cd',aux,0);
opt = greyestOptions('InitialState','backcast','Display','on');
pend_model = pem(z,pend_model,opt);
figure();
compare(z_post,pend_model);
また,この時に推測されたパラメタ値について以下に示す.
表7 同定されたパラメタ
| 定数名 | 数値 |
|---|---|
| I | -0.02263 |
| J | 3.497e-05 |
| $D_{\phi}$ | 0.001016 |
| $D_{\theta}$ | 0.0009073 |
| $K_T$ | 0.006198 |
| $K_E$ | 0.008441 |
| $R_a$ | 10.4 |
| $J_m$ | 5.208e-08 |
本体の慣性モーメントが負値になっていることは現実的にはありえないことであるが,今回はそのままこの値を用いて制御を行った.
実機制御
LQRによる状態フィードバックゲインの算出
LQレギュレータを用いた状態フィードバックゲインを算出した.この時用いたスクリプトをset_parameter.mとして示す.
表8 set_parameter.m
clear all;
close all;
format compact;
M=0.641; % [kg]本体の質量
m=0.0485; % [kg]車輪の質量 2つ合わせたもの回転部全部のということ
L=0.065; % [m]車軸から本体部重心への距離
r=0.0575/2; % [m]車輪の半径
g=9.81; % [m/s^2]重力加速度
n = 19 * (50/12);
I=-0.02263; % [kg m^2]本体の慣性モーメント
J=3.497e-05; % [kg m^2]車輪の慣性モーメント
D_phi=0.001016; % [kg m^2/s]車輪の粘性摩擦係数
D_theta=0.0009073; % [kg m^2/s]本体の粘性摩擦係数
Kt = 0.006198;%mNm/A
Ke = 0.008441;%V/(rad/s)
Ra = 10.4;
Jm=5.208e-08;
%式を簡略化するための定数
a=(m+M) * r*r + J;
b=M*r*L;
c=M*M*L + I;
d=M*g*L;
%式の簡略化のための定数
E = a + Jm * n * n;
F = a + b;
G = D_phi + (Kt * Ke * n * n)/Ra;
H = a + 2*b + c;
%最終的に出てくる状態方程式の係数
a21 = -E*d/(F*F - E * H);
a22 = E*D_theta / (F*F - E*H);
a23 = -F*G / (F*F - E*H);
a31 = F*d / (F*F - E*H);
a32 = F * D_theta / (F*F - E*H);
a33 = G * H /(F*F - E*H);
b2 = F*Kt*n / (Ra * (F*F - E*H) );
b3 = -H*Kt*n / (Ra * (F*F - E*H) );
STATE_A = [0 1 0
a21 a22 a23
a31 a32 a33];
STATE_B = [0;b2;b3];
Q=[1,0,0;
0,2,0;
0,0,1];
R=20;
K=-lqr(STATE_A,STATE_B,Q,R)
実際に算出されたゲインは,
$$
K^T=[51.3362 , 6.3195 , 1.4149]
$$
となった.
実機実験
実際に実機で制御を行った結果の動画を以下のURLに示す.制御周期は20msとした.
https://www.youtube.com/watch?v=s30WJX81Xuo
動画では分かりづらいが,ある程度の倒立動作を実現している.次に,求めたパラメタを元に,手動で調整を行った場合の動画を示す.
https://www.youtube.com/watch?v=85HMHGiH8zQ
位置のフィードバックが無いため,位置がずれ続けているが,倒立制御がより綺麗に行えていることが確認できる.
さいごに
以上で,車輪型倒立振子の同定から,その制御までを行った.記事の製作も駆け足であったため,内容の不備についてはご指摘いただければ幸いです.また,今回の同定手法が本当に正しいものであるか検証が十分ではなく,たまたまうまくいっただけの可能性もありますのでご了承ください.
参考文献
[1]MATLABによる制御のための上級システム同定 足立修一 著
[2]倒立振子で学ぶ制御工学 川田昌克 編著
[3]倒立2輪ロボットの安定化制御 佐藤 光 木澤 悟
補足
倒立振子のパラメータ調整手順については、以下のwebページが大変わかりやすいです。
http://www.mech.tohoku-gakuin.ac.jp/rde/contents/tech/BallIPMini/techinfo.html#eRgkKfLoemPcAncCQcCicCacCcBhjfUt