Unsupervised Learning
Clustering: K-means Algorithm
K-means Algorithm:
- randomly initialize K cluster centroids $\mu_1,\mu_2,...,\mu_K$
- cluster assignment: for i=1:m, $c^{(i)}$:=index of cluster centroid closest to x(i)
- move centroid: for k=1:K, $\mu_k$:=average (mean) of points assigned to cluster k
-
Input:
-
K(number of clusters)
-
Training set {$x^{(1)},x^{(2)},...,x^{(m)}$}
-
K-means Optimization Objective:
min\,J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_K) = \frac{1}{m}\sum_{i=1}^m||\,x^{(i)}-\mu_{c^{(i)}}||^2
- $c^{(i)}$ = index of cluster (1,2,...,K) to which example x(i) is currently assigned
- $\mu_k$ = cluster centroid k
- $\mu_{c^{(i)}}$ = cluster centroid of cluster to which example x(i) has been assigend
Random Initialization
- should have K < m
- randomly pick K training examples
- Set $\mu_1,...,\mu_K$ equal to these K examples
For i = 1:100 {
Randomly initialize K-means
Run K-means. Get $c^{(1)},...,c^{(m)},\mu_1,...,\mu_K$
Compute cost function (distortion) $J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_K)$
}
=>Pick clustering that gave lowest cost J
Dimensionality Reduction: Principal Component Analysis (PCA)
Purposes:
- To reduce the dimension of the input data so as to speed up a learning algorithm
- To compress data to reduce the memory of disk space
- To visualize high-dimensional data (by choosing k=2 or 3)
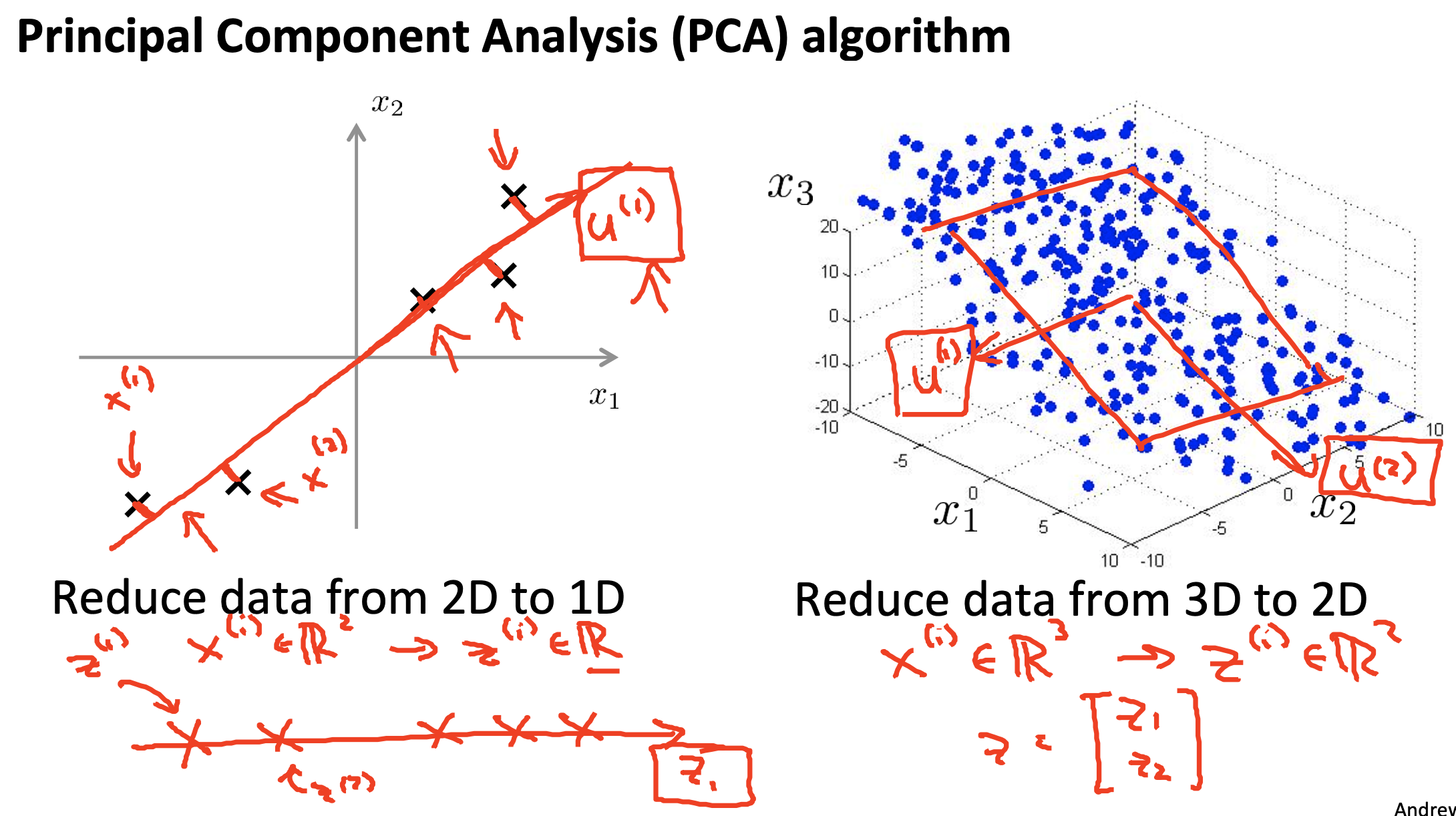
PCA Algorithm
- Data Preprocessing(feature scaling/mean normalization)
- Compute "covariance matrix"
Σ(Sigma) = \frac{1}{m}\sum_{i=1}^n(x^{(i)})(x^{(i)})^T
-
Compute “eigenvectors” of matrix Σ(Sigma):
[U,S,V] = svd(Sigma); -
$U_{reduce} = U(:, 1:k)$
-
z = $U_{reduce}'*x$
Reconstruction from compressed representation
$X_{approx} = U_{reduce} * Z$
Choosing the number of principal components k
