概要
活性化関数とは、ニューラルネットワーク内に置かれる、線形変換の後に適用する非線形関数のこと。入力層の総和に対して最終的な出力値を決定するために用いられることが多い。
以下の図における$ \varphi $が活性化関数に対応する。
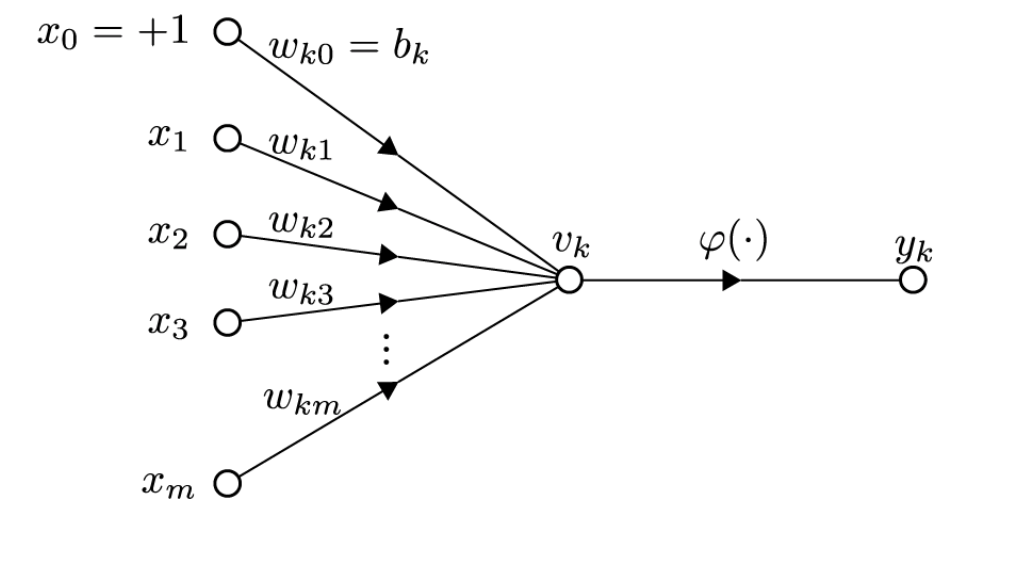
引用元:活性化関数 Wikipedia
活性化関数の役割
ニューラルネットワークの基本的な構造は、線形変換である。しかしながら、線形変換だけでは表すことができないものがある。そこで出力層に非線形的な活性化関数を置いておくことで、表現の幅が広がるのである。
なぜ非線形関数を用いるのか？？
線形関数では、どんなに層を深くしても同じことを１層で表現することが可能になってしまうからである。非線形関数を用いることで、多層にする利点を見いだすことができるというわけだ。
活性化関数の種類
活性化関数にはいくつか代表的なものがある。
シグモイド関数
ニューラルネットワークにおいてよく使われる関数の一つが、シグモイド関数である。シグモイド関数は以下の式で表される。
h(x) = \frac{1}{1 + e^{-x}}
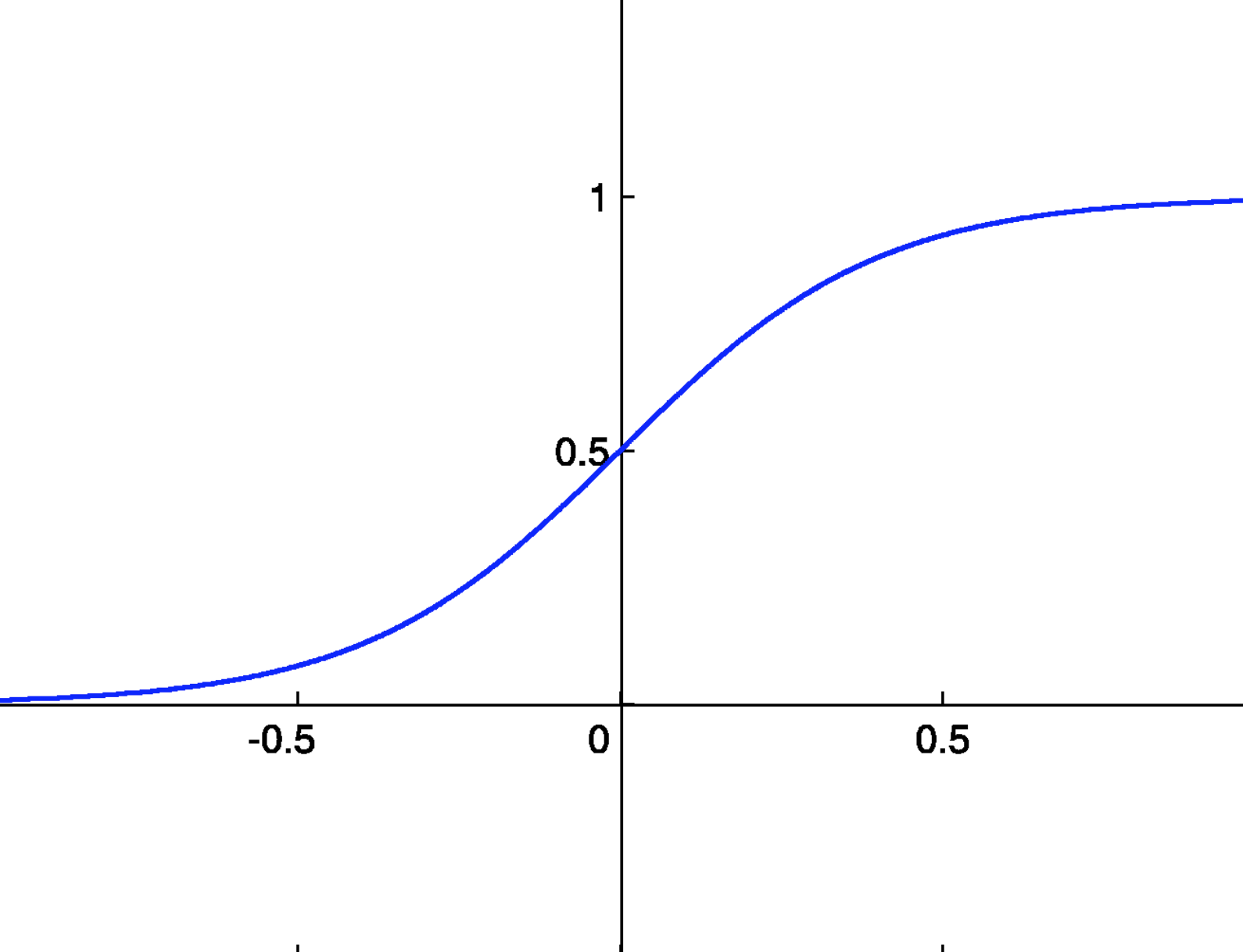シグモイド関数は全ての実入力に対して、０〜１の連続した値を出力する関数である。入力が小さい時は０に近く、出力が大きい時は１に近く。また0に対しては0.5を出力する。
ステップ関数
ステップ関数を用いることで0と1の2値出力をすることができる。
$$
f(x) =
\begin{cases}
1 & (x \geq 0)\\
0 & (x < 0)
\end{cases}
$$
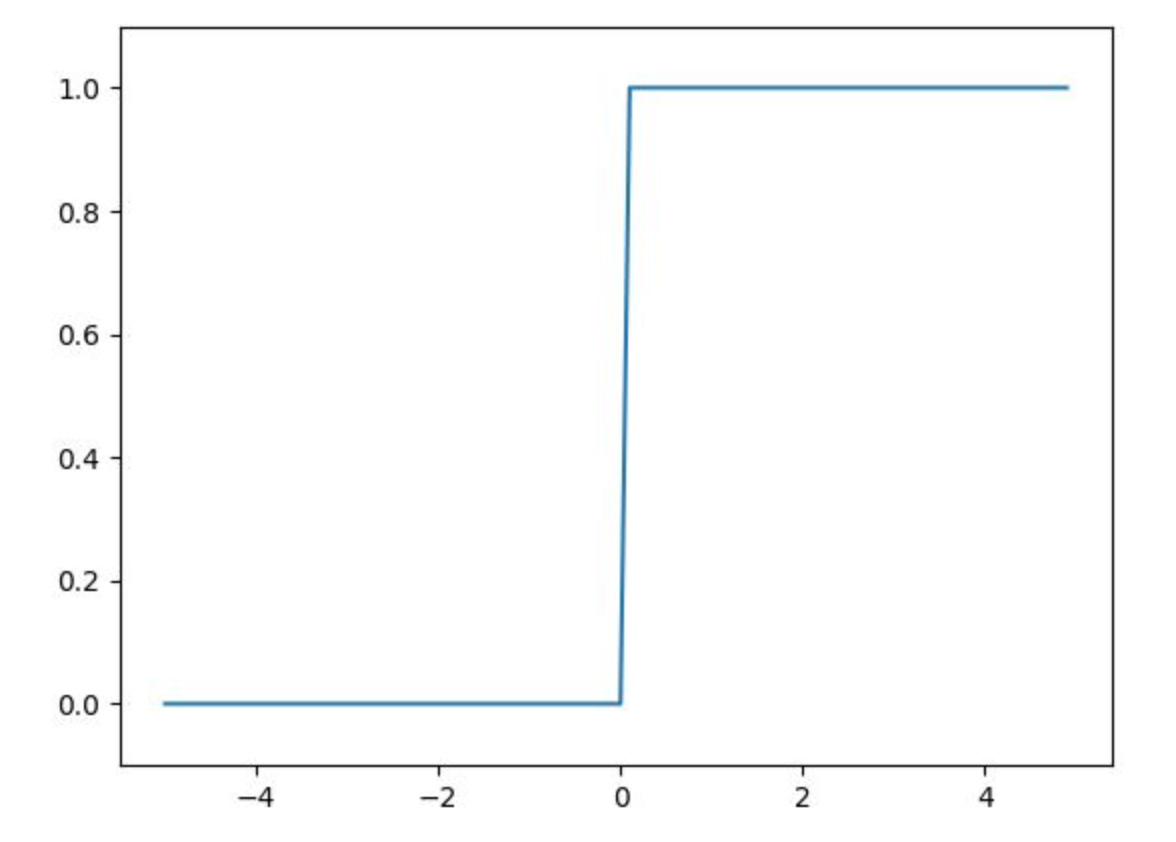
シグモイド関数と同じく0~1のまで出力となっているが、0か1しか出力ができないので表現力はシグモイド関数よりも乏しいと言えるかもしれない。
ReLU関数
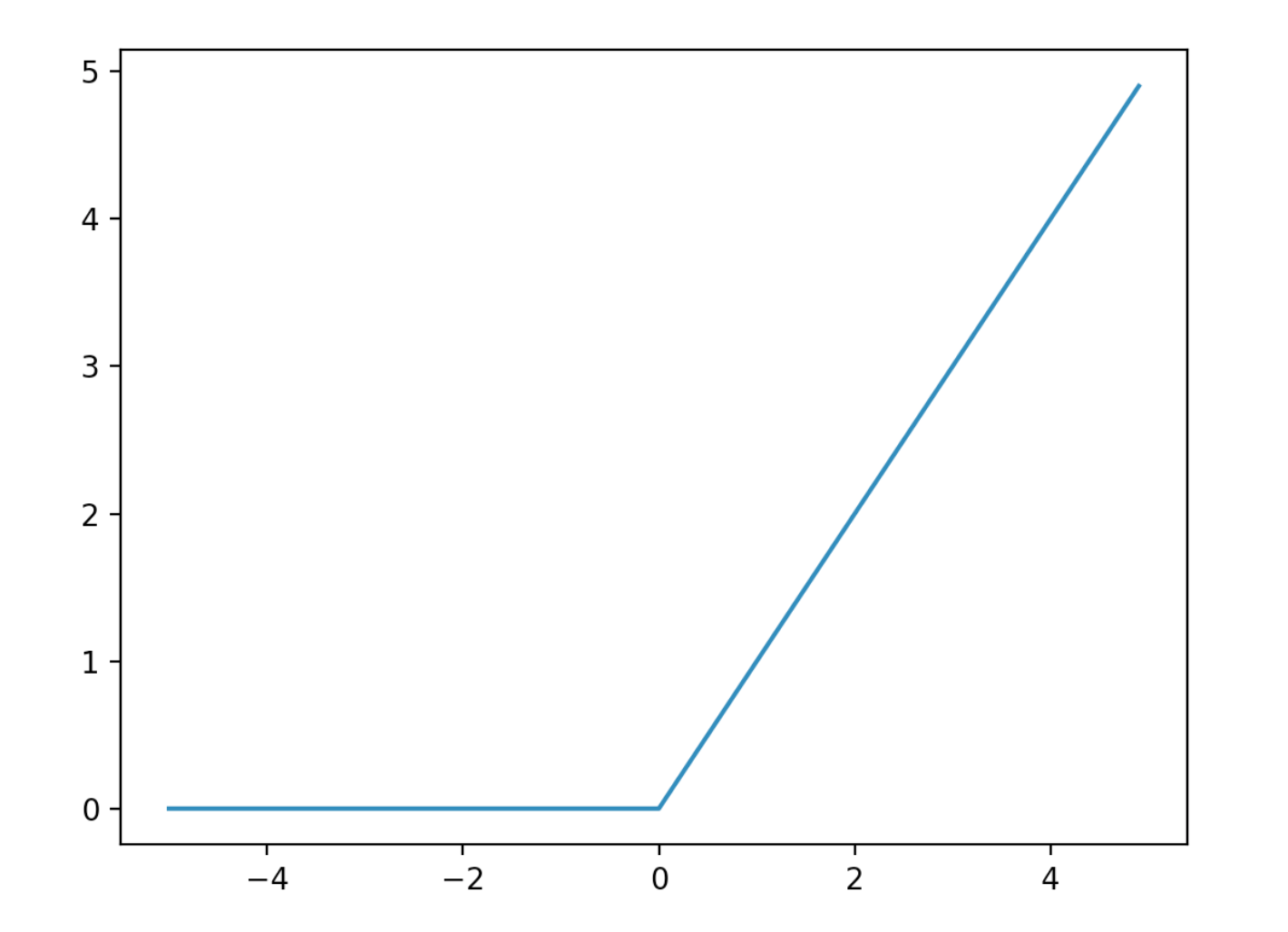
最近のニューラルネットワークにおいて頻繁に使われているのが、ReLU関数である。
ReLU関数は、ランプ関数ともいい、入力が0より大きければそのままの値を、0より小さければ0を出力する活性化関数である。
$$
f(x) =
\begin{cases}
x & (x \geq 0)\\
0 & (x < 0)
\end{cases}
$$
恒等関数
恒等関数とは入力された値をそのまま出力する関数である。
回帰問題においては出力層においては恒等関数を用いる。
ソフトマックス関数
ソフトマックス関数とは分類問題の出力層に置かれる関数である。
$$
y_k = \frac{exp(a_k)}{\sum_{i = 1}^{n} exp(a_i)}
$$
ソフトマックス関数はn個の入力$a_1$ ~ $a_n $から、出力$y_1$ ~ $y_n $を得る。
$y_1$ ~ $y_n $はそれぞれ0~1であり、総和が１であることからソフトマックス関数の出力は確率と捉えることができる。
分類問題では、ソフトマックスの関数の出力の最大値のクラスを答えとするのが一般的である。
まとめ
活性化関数はニューラルネットワークにおける非線形関数であり、活性化関数を用いることで表現の幅が広がる。
活性化関数は様々な種類があり、それぞれ個別の特徴があり、場面ごとに使い分けられる。