#勾配法の欠点
勾配法では、微分を用いて勾配を計算し、それらを用いてパラメータを更新を行っていた。しかしながら、実際のニューラルネットワークはかなり複雑であり、微分は数値計算的にはとても時間がかかり非効率である。
そこで、利用されるのが誤差逆伝播法である。
#計算グラフを用いた誤差逆伝播法
誤差逆伝播法を理解するには計算グラフを利用するのが便利である。
例として、１本１００円の鉛筆を２本、１個３０円の消しゴムを３個、消費税が１０％の場合を考える。
この問題の計算を以下のようにグラフで表す。
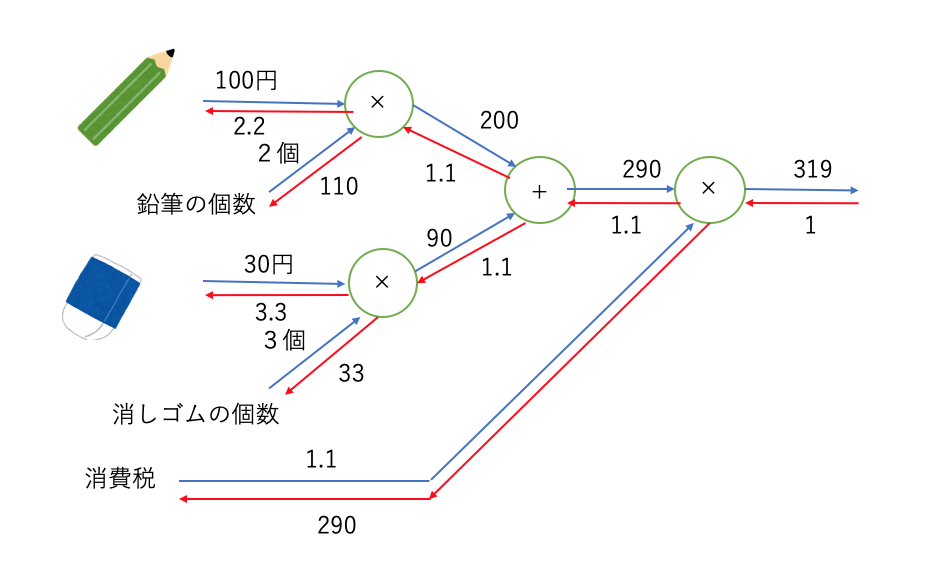
グラフを見ると、矢印の流れが２つある。
左から右へと伝わる(順伝播)部分の計算は通常の四則演算である。
一方、右から左へ伝わる流れ(逆伝播)は、各値を１増加させた時、１番右の値(例では合計金額)がどれだけ増加するかを表している。
つまりこの方法を用いれば、各パラメータの勾配を求めることができる。これが誤差逆伝播法である。
#逆伝播の計算方法
まず１番右の逆伝播を１にし、そこから各ノードで逆伝播を計算していく。
以下のように、xを入力とし $y=f(x)$を出力とするノードがあるとする。
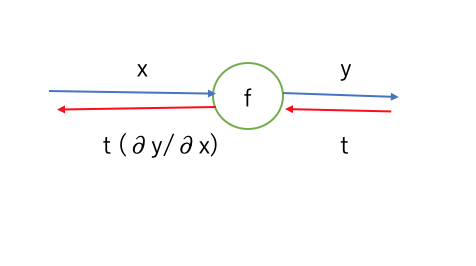
この時、yでの逆伝播をtとすると、xの逆伝播は$$t(\frac{\partial y}{\partial x})$$
となる。
ここからは各ノードの逆伝播について紹介していく。
###＋ノード
＋ノードは単純に同じ値をそのまま左へ逆伝播させるだけである。
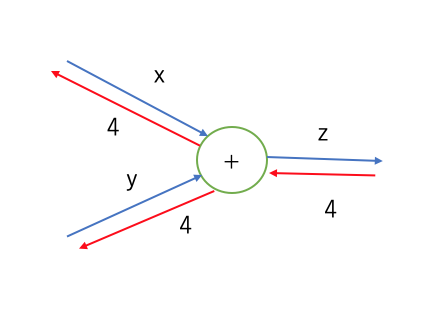
z=x+yであるので、zをx,yでそれぞれ微分すると1となる。これが、そのまま左へ逆伝播する所以である。
###×ノード
×ノードは相手の値を逆伝播にかけて伝播させる。
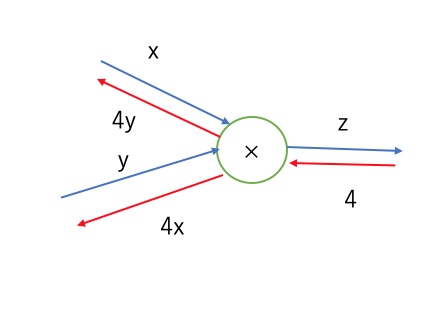
z=xyなので、zをx,yで微分とすると、y,xとなる。よってxはyを、yはxをかけるのである。
dotノード
行列の積は、以下のようになる。行列の積の順序に注意。
活性化関数も逆伝播を求めることができる。
###ReLUノード
ReLUの微分は、
$$
\frac{\partial y}{\partial x}=
\begin{cases}
1 & (x \geq 0)\
0 & (x < 0)
\end{cases}
$$
なので、x≥0ではそのまま伝播し、x<0では0となる。
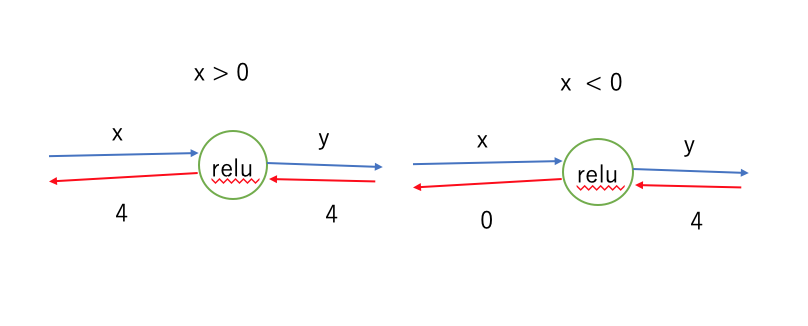
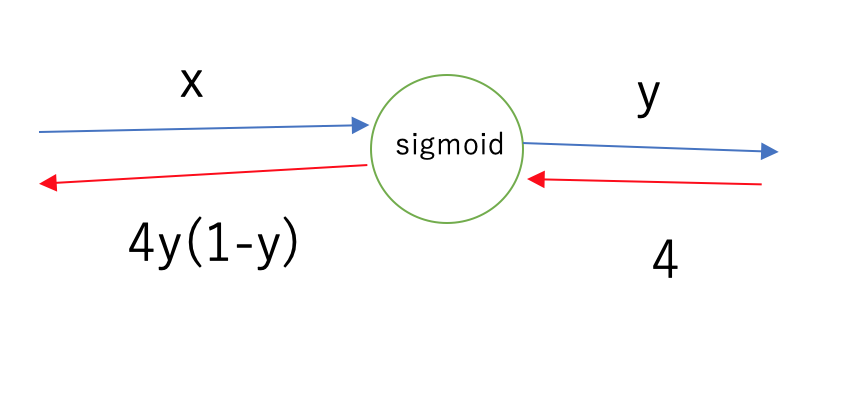
###Sigmoidノード
計算は省略するが、以下のようになる。
#Softmaxノード
Softmaxノードはクロスエントロピー誤差と一緒に考えると、便利である。
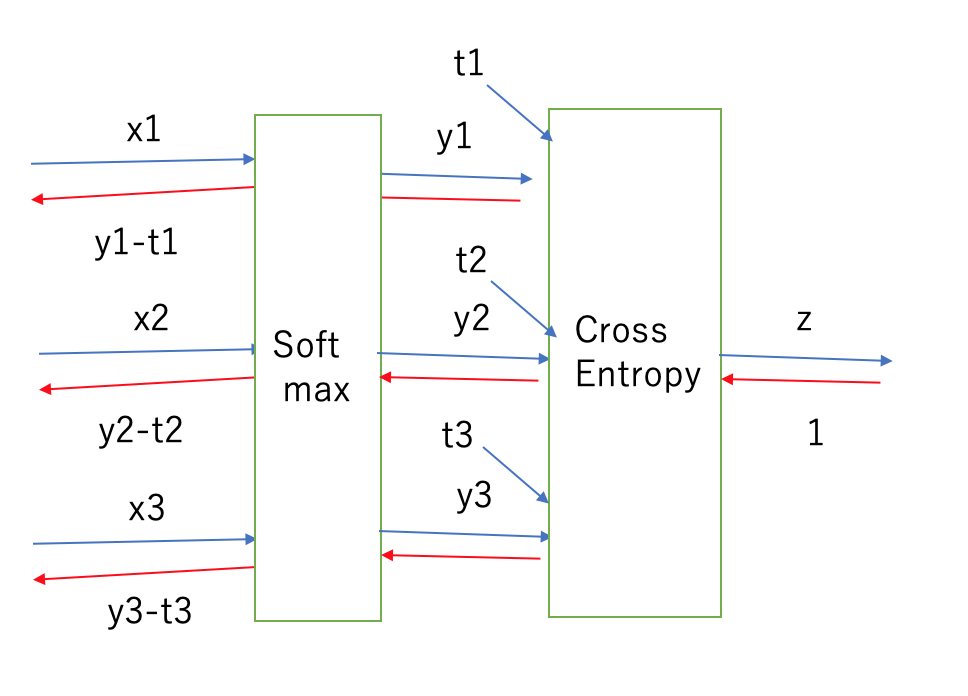
なお、t1~t3は正解ラベルである。
それぞれの逆伝播はやや複雑だが、組み合わせるとSoftmaxノード前の逆伝播が正解ラベルとSoftmaxの出力との差と、単純な形になっている。
クロスエントロピー誤差は、このように逆伝播が綺麗な形になるように設計された関数なのである。
そのほかの損失関数に関しても、逆伝播が綺麗になるように設計されたものが多い。
#まとめ
誤差逆伝播法は、勾配をより簡単に求めるための手法であり、計算グラフを用いると理解しやすい。
逆伝播は、各パラメータの増加に対する最終的な値の増分を表している。
損失関数の多くは、逆伝播が単純な形になるように設計されている。