勾配って何??
簡単に言えば、多変数関数における傾きのようなもので、1変数関数のようにスカラーではなく、ベクトルとなる。
勾配が示すベクトルは、各点において最も数が大きくなる方向と言える。(-をつければ、各点において最も数が小さくなる方向とも言える。)
実際に求める時には、全ての変数で偏微分し、ベクトルで表すと勾配になる。具体例を挙げてみてみよう。
$f(x,y) = x^{2} + y^{2}$をx,yで偏微分すると、それぞれ2x,2yとなる。
よって、点(0,0),(0,1),(1,0)の勾配は(0,0),(0,2),(2,0)となる。
勾配と損失関数
ニューラルネットワークの学習では、重みやバイアスといったパラメータを変化させ、以前説明した損失関数を小さくしていく。
しかし一般的には損失関数は複雑で、どの方向にパラメータを動かせば良いかわからない。そこで勾配を用いると、簡単に損失関数が小さくなる方向がわかる。
しかしながら、必ずしも勾配は損失関数を最小値へと導くわけではない。
下図を見てみよう。(この場合は勾配というよりも傾きだが、、)
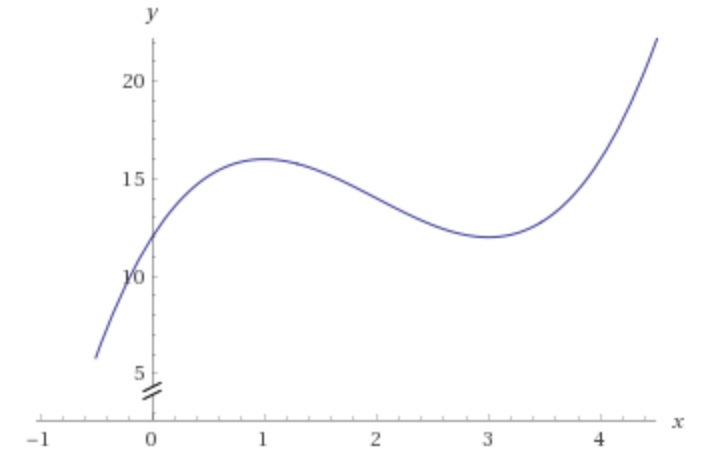
仮にx=5から勾配に従っていくとx=3で勾配が0になり停滞する。しかしながら、x<0ではもっと値が小さくなる。このように勾配に従っているだけでは、極小値で停滞してしまい、最小値にたどり着かないことがある。
勾配降下法って?
先ほど説明したように、必ず最小値にたどり着くわけではないが、損失関数を小さくすることができる。
勾配降下法とは、その点における勾配に従ってある一定距離進み、その進んだ先での勾配を求めて、またそこから勾配に従ってある一定距離進む..というのを繰り返す。
このようにして損失関数の値を小さくしていく方法が勾配降下法である。
ニューラルネットワーク以外でも、最適化の分野でよく使われる方法です。
実際の勾配降下法を式で表すと、
$$
x_n= x_{n-1} - \eta \frac{\partial f}{\partial x} \
y_n = y_{n-1} - \eta \frac{\partial f}{\partial y}
$$
となる。なお、$f$は損失関数、$\eta$は学習率である。
学習率は、一回の学習でどれだけ値を更新するかを定めたパラメータで、事前に定める値である。
実際の学習の流れ
①学習データの中から無作為に一部のデータを選ぶ。(このデータをミニバッチという。)
②ミニバッチを用いて、各パラメータの勾配を計算する。
③勾配降下法に従って、各パラメータを更新する。
上記の①〜③を繰り返し、パラメータを更新していく。
無作為にミニバッチを選ぶ勾配降下法を、**確率的勾配降下法(SGD)**という。
まとめ
勾配降下法とは、損失関数を小さくするために、勾配を用いてパラメータを更新する手法であり、ニューラルネットワークの学習において使われる。
必ずしも、損失関数が最小になるとは限らないが、この方法を用いることで、損失関数を小さくすることができる。