🔰PyTorchでニューラルネットワーク基礎 #11 【時系列分析・系列変換】

Last updated at 2025-08-04Posted at 2025-07-23

概要

個人的な備忘録を兼ねたPyTorchの基本的な解説とまとめです。LSTMを利用した日経225を利用した予測の３回目となります。今回も日経225の始値を予測するタイプですが、第８回や第９回とは異なり、複数期先までの予測を目標としています。LSTMを利用した系列変換モデルによって、毎期5期先まで予測するモデルを作成してみます。下記のようなグラフが完成します。

図：5期先まで予測したものをつなげたグラフ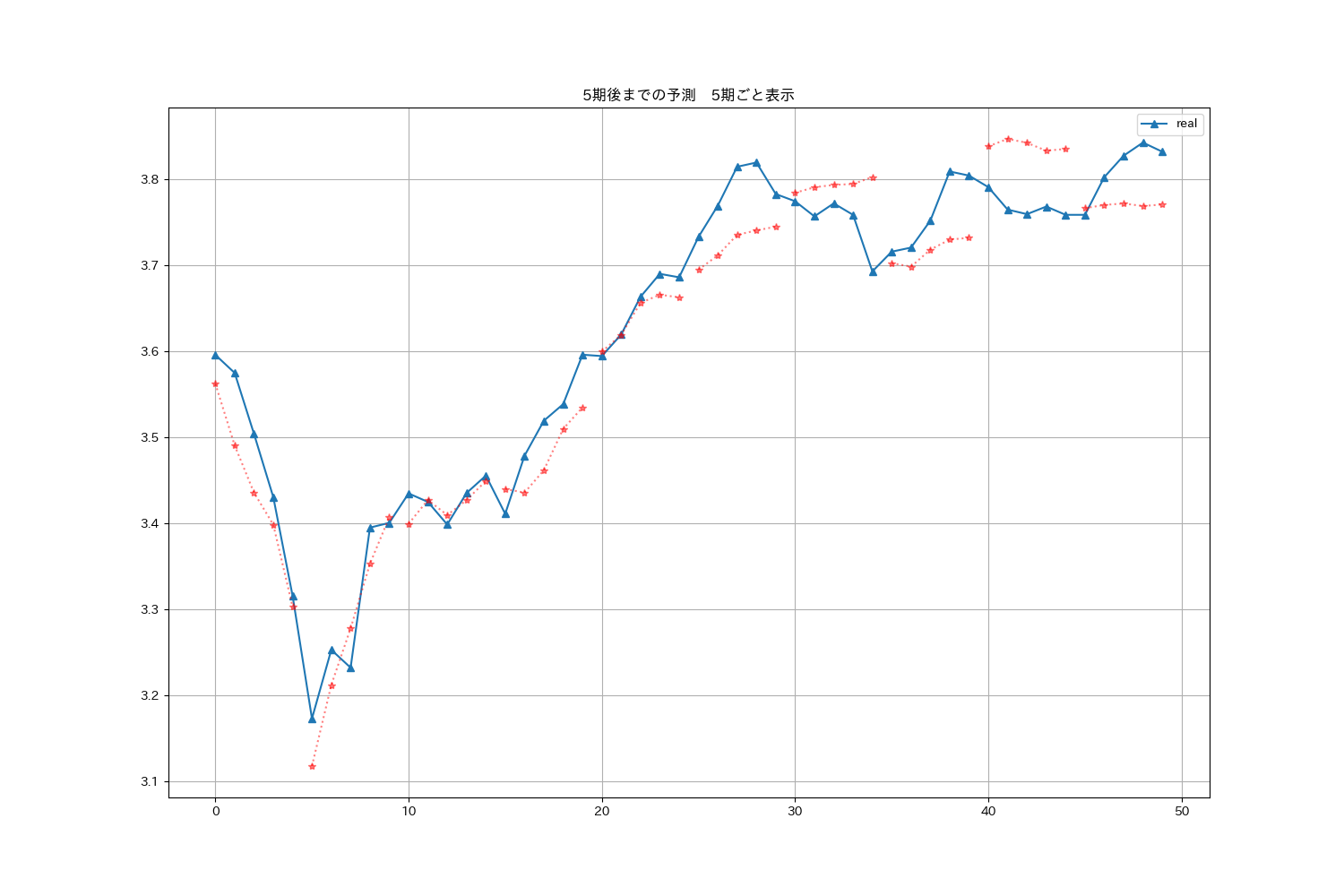

方針

できるだけ同じコード進行
できるだけ簡潔（細かい内容は割愛）
特徴量などの部分，あえて数値で記入（どのように変わるかがわかりやすい）

演習用のファイル

データ：nikkei_225.csv
コード：sample_11.ipynb

1. 💹 RNNと系列変換

1.1 RNNの復習

$t-1$期までの過去の情報の特徴量である履歴$h_{t-1}$とその時点でのデータ$x_t$から
$$h_t=\tanh(W_x x_t + W_h h_{t-1} + b)$$
に従って$t$期までの情報の特徴量を導出していくのが再帰ネットワークの基本的になります。

$x_t$：時刻$t$での新しい入力データ
$h_{t-1}$：前の時刻で計算した結果（これが「過去の情報」）
$h_t$：現在計算している結果（次の時刻では過去の情報$h_{t-1}$となる）

$t$期の特徴量を計算するには、$t-1$期の情報である$h_{t-1}$が必要になる点がポイントです。特に、LSTMの場合は、$t-1$期の履歴とメモリーセルの情報
$$(h_{t-1}, c_{t-1})$$
が必要になります。

1.2 系列変換モデル (sequence to sequence model)

系列変換モデルは、英語表記で表現されているように、ある系列が入力されると、何かしらの系列が出力されるというモデルになります。「こんにちは」の入力に対して「やあ！」と返事があるのと似ていますね

例
時系列データの(1, 2, 3, 4, 5)が入力されると、時系列の(6, 7, 8)のように続きが出力されるようなタイプを系列変換と呼んでいるようです。

入力される系列	出力される系列
1, 2, 3, 4, 5	6, 7, 8

系列変換モデルは

エンコーダー (encoder)：入力データから特徴量を抽出する部分
デコーダー (decoder)：抽出した特徴量から時系列のデータを出力する部分

という２種類のネットワーク構造から構成されます。今回はエンコーダーにLSTM、デコーダーにもLSTMを利用するタイプのネットワークを作成していきます。

これまで

１期〜５期までのデータから、６期目（次の期）を予測

今回 (系列変換モデル)

１期〜５期までのデータから、６期目〜10期目までの5期間を予測
図のようなネットワーク構造となります。

図：系列変換モデル

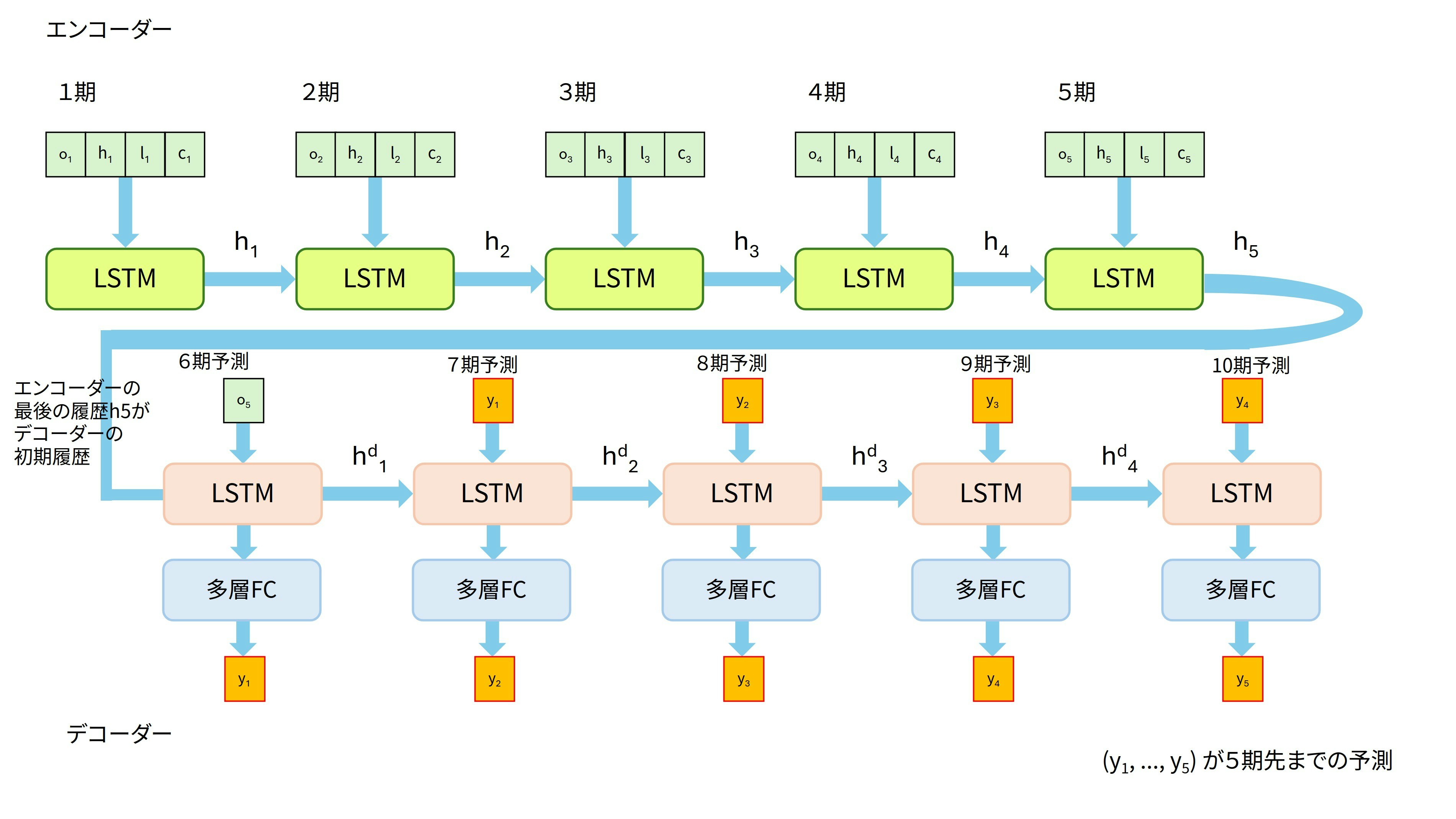
PyTorchによるプログラムの流れを確認します。基本的に下記の５つの流れとなります。Juypyter Labなどで実際に入力しながら進めるのがオススメ

データの読み込みとtorchテンソルへの変換　(2.1)
ネットワークモデルの定義と作成　(2.2)
誤差関数と誤差最小化の手法の選択　(2.3)
変数更新のループ　(2.4)
検証　(2.5)

2. 🤖 コードと解説

2.0 データについて

日経225のデータをyfinanceやpandas_datareaderなどで取得します。第8回と同一のデータを利用します。

Date	Open	High	Low	Close	Volume
2021-01-04	27575.57	27602.11	27042.32	27258.38	51500000
2021-01-05	27151.38	27279.78	27073.46	27158.63	55000000
2021-01-06	27102.85	27196.40	27002.18	27055.94	72700000
︙	︙	︙	︙	︙	︙
2025-06-18	38364.16	38885.15	38364.16	38885.15	110000000
2025-06-19	38858.52	38870.55	38488.34	38488.34	89300000

始値(Open)を予測する形で演習を進めていきます。始値のグラフを描画してみましょう。青色の線が日経225の始値の折れ線グラフとなります。

学習用データとテスト用データに分割します。グラフの赤い線の右側100期をテスト用のデータとして使います。残りの左側を学習用のデータとします。学習用データで学習させて、「右側の100期間を予測できるのか？」が主目標となります。

2021年以降の日経225の値は、3万円前後の数値になることがほとんどです。誤差計算時の損失の値が大きくなりすぎないように、変数の更新がうまく行われるように、「1万円で割り算して数値を小さく」 しておきます。これで、ほとんどの値が2.5〜4に収まるはずです。

ここまでの内容をまとめたコードが次になります。

データの読み込み

import pandas as pd
import numpy as np
import torch
import torch.nn as nn

# CSVファイルの読み込み
data = pd.read_csv("./data/nikkei_225.csv")

# 日経225の値を10,000円で割り算して値を小さくする
scaling_factor = 10_000
x_open = data["Open"]/scaling_factor
x_high = data["High"]/scaling_factor
x_low = data["Low"]/scaling_factor
x_close = data["Close"]/scaling_factor

2.1 データセットの作成とtorchテンソルへの変換

系列変換モデルで学習できる形にデータを前処理します。１期〜５期までのデータから、６期目〜10期目までの5期間の始値を予測させるようにデータセットを作っていきます。具体的には、入力データは株価の始値・高値・安値・終値データを窓サイズ５で区切って、その窓を1つずつスライドさせながらデータ作成していきます。教師データも5期分を予測させるので、窓サイズ５の始値データ になります。予測させる期間の数５と窓サイズが同じになります。

入力データ	教師データ
１期　２期　３期　４期　５期	６期　７期　８期　９期　１０期
$x_1,~x_2,~x_3,~x_4,~x_5$	$t_1,~t_2,~t_3,~t_4,~t_5$

注意点は２箇所

教師データは、5期目から窓サイズ５で移動させて作成
５期先までの予測なので、入力データの終端位置に注意

入力データの注意点
変更前

XO = [... for start in range(len(data)-win_size)]

変更後

XO = [... for start in range(len(data)-win_size-dec_win_size)]

CSVファイルの読み込みから窓サイズでの分割までのコードです。スマートに一度に変換ではなく、地味に同じことを繰り返しで書きました

win_size = 5      # 入力データの窓サイズ
dec_win_size = 5  # 教師データの窓サイズ

XO = [x_open[start:start+win_size] for start in range(len(data)-win_size-dec_win_size)]
XH = [x_high[start:start+win_size] for start in range(len(data)-win_size-dec_win_size)]
XL = [x_low[start:start+win_size] for start in range(len(data)-win_size-dec_win_size)]
XC = [x_close[start:start+win_size] for start in range(len(data)-win_size-dec_win_size)]
# 教師データ win_size=5期からスタート
TO = [x_open[start:start+dec_win_size] for start in range(win_size, len(data)-dec_win_size)]
# 入力データ
xo = np.array(XO)
xh = np.array(XH)
xl = np.array(XL)
xc = np.array(XC)
# 教師データ
t  = np.array(TO)

xo = xo.reshape(xo.shape[0], xo.shape[1], 1)
xh = xh.reshape(xh.shape[0], xh.shape[1], 1)
xl = xl.reshape(xl.shape[0], xl.shape[1], 1)
xc = xc.reshape(xc.shape[0], xc.shape[1], 1)

t = t.reshape(t.shape[0], t.shape[1])         # 最終的な教師データ
x = np.concatenate([xo, xh, xl, xc], axis=2)  # 最終的な入力データ

窓サイズで区切った始値・高値・安値・終値の４種類を入力データに使います。
５個区切りデータ（XO、XH、XL、XC）は、それぞれ窓サイズ５で特徴量が１つの状況です。これを結合して、（バッチサイズ、５，４）の形状に変換します。

実際に表示するとわかるのですが、上記のコードだとXOやTOはタイプが入り乱れています。最終的にtorch.FloatTensor()の形になればよいので、スマートではありませんが力技で押し切るコードにしました一旦、numpy配列にして形式を整えてしまいましょう

入力データxの形状が、（バッチサイズ、系列長の５、特徴量の４）、教師データの形状が、（バッチサイズ、系列長の５）になっていることが確認できます。xをLSTMに入れることからネットワークが始まります。その前に、xとtをFloatTensorに変換して、学習用データとテスト用データに分割します。前半部分を学習用、後半部分をテスト用と前後に分割します。

torchテンソルへ変換

device = "cuda" if torch.cuda.is_available() else "cpu"
x = torch.FloatTensor(x).to(device)
t = torch.FloatTensor(t).to(device)

period = 100
x_train = x[:-period]
x_test = x[-period:]
t_train = t[:-period]
t_test = t[-period:]

# 入力する特徴量は１次元
# x_train.shape : torch.size([987, 5, 4])
# x_test.shape :  torch.Size([100, 5, 4])
# t_train.shape : torch.Size([987, 1])
# t_test.shape :  torch.Size([100, 1])

2.2 ネットワークモデルの定義と作成

記号
$x_1,~x_2,~x_3,~x_4,~x_5$：入力データで１期〜５期の始値、高値、安値、終値
$t_1,~t_2,~t_3,~t_4,~t_5$：入力データに対応する教師データで６期〜10期の始値

教師データの添え字が、$t_1$で６期目の始値を表します

LSTMを利用した系列変換モデルで５期先までの予測を扱っていきます。オレンジ色っぽい平行四辺形で囲われた4次元の値$x_1=(xo_1, xh_1, xl_1, xc_1)$から順番に入力されます。LSTMに入力される特徴量は4つなので、input_size=4となります。LSTMの最終的な出力であるh5とc5が過去の５日分の情報を再帰的に考慮した特徴量になります。h5、c5をデコーダーのLSTMの初期値として利用します。

図：エンコーダー部分

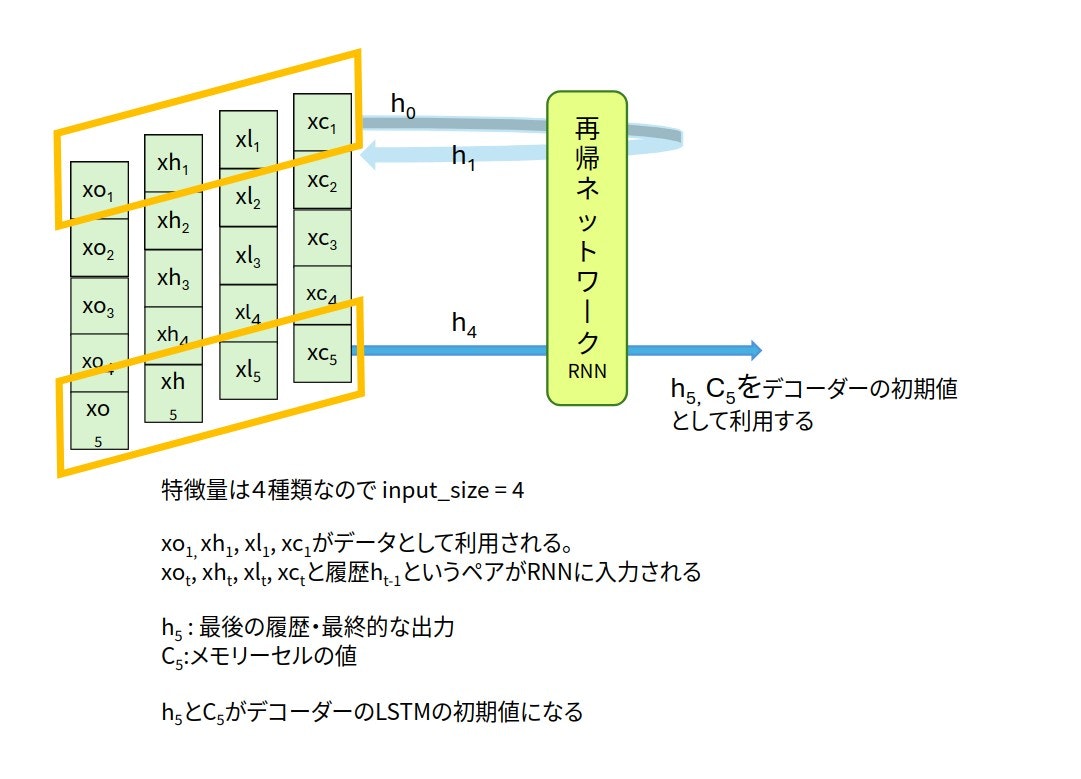
PyTorchでのLSTMの書き方のポイントをまとめておきます。LSTMの出力は３種類あり、履歴hとセルcをエンコーダー側の出力として利用します。

LSTM層の書き方
nn.LSTM(input_size, hidden_size, num_layers, batch_first)

input_size : 入力される特徴量の次元
hidden_size : 出力される隠れ層の特徴量の次元
num_layers :　再帰するLSTMの数、デフォルトはnum_layers=1
batch_first : Trueで（バッチサイズ、系列長、特徴量）の形状

batch_first=TrueでのLSTMの出力値
o, (h, c) = lstm(x)

o : すべての時点での最終層（一番最後layer）の隠れ状態の出力
h : 最後の時点でのすべての隠れ層の出力
c : 最後の時点におけるセル状態

詳細はPyTorchの公式ドキュメントに記載されています。

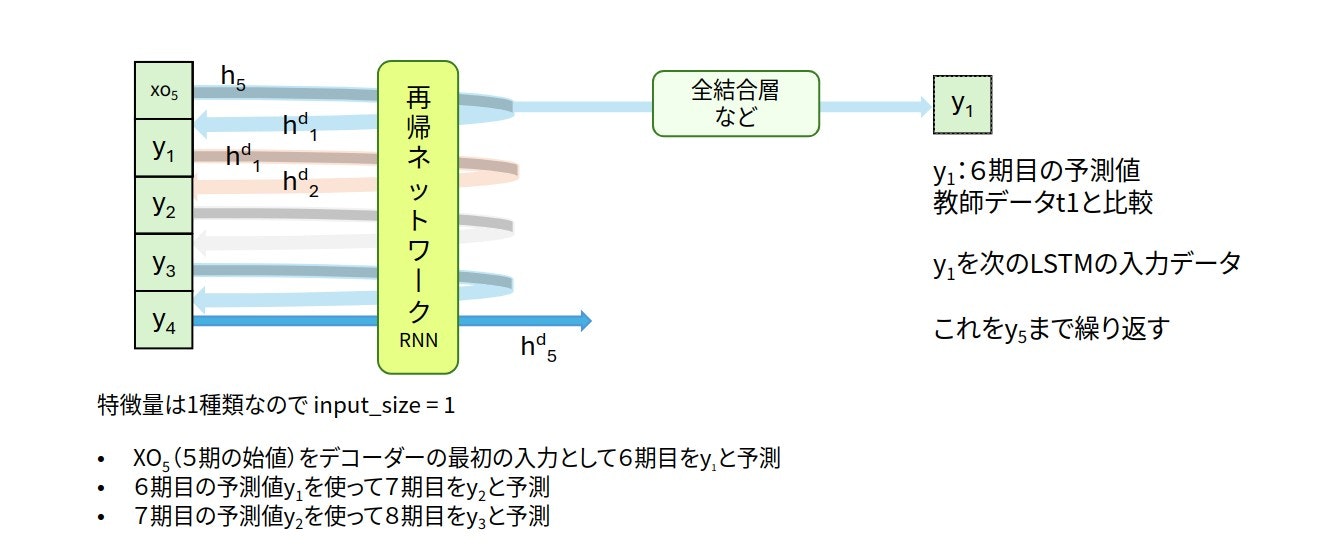
デコーダー部分では、従来の「1期先のみを予測するモデル」とは異なるアプローチを採用します。ここでは5期先までの予測を行うため、LSTMを使って予測値を段階的に生成していきます。具体的には、まず1期先を予測し、その予測結果を次の入力として2期先を予測、さらにその結果で3期先を予測……というように、予測値を連鎖的に生成して5期分の時系列予測をしていきます。

エンコーダーから引き継いだ隠れ状態h5、セル状態c5をデコーダーの最初のLSTMの初期値とし、入力データには5期の始値$xo_5$を使います。LSTMの出力は
$$o, (h, c) = \mbox{lstm}(xo_5, (h_5, c_5))$$
のように計算されます。oまたはhから全結合層などを利用して６期目の予測値を$y_1$と計算します¹。予測値$y_1$と６期目の教師データである$t_1$との誤差を求めます。$y_1$を次のLSTMの入力データとして再帰ネットワークの計算が始まります。７期目の予測値$y_2$と教師データである$t_2$を比較して誤差を求めます。最終的に10期目の予測値$y_5$と教師データ$t_5$から誤差が求まります。この誤差を小さくするようにパラメータを更新することになります。

最終的な予測値は($y_1$, $y_2$, $y_3$, $y_4$, $y_5$)の5つとなります。これが6期目〜10期目までの5期分の予測となります。

図：デコーダー部分

実際のネットワーク構造ですが、デコーダーでの予測ループ部分が一見複雑に見えます。ネットワーク構造自体は、LSTM2つと全結合層だけなので本質的に単純です。エンコーダー側は４次元の入力値で５回再帰的に繰り返し、履歴$h_5$とセル状態$c_5$をデコーダーのLSTMに渡します。デコーダーは１次元の入力値で次の期の日経225を予測していくという形になります。図にまとめると、よくある系列変換の解説図になります。

図：系列変換モデル

エンコーダー部分はLSTMだけです。enc_lstmとしています。デコーダーは、LSTMと全結合層や活性化関数から構成されます。デコーダーのLSTMをdec_lstmとしています。

モデル定義

class DNN(nn.Module):
    def __init__(self):
        super().__init__()
        # エンコーダー
        self.enc_lstm = nn.LSTM(input_size=4, hidden_size=100, num_layers=1, batch_first=True)
        # デコーダー
        self.dec_lstm = nn.LSTM(input_size=1, hidden_size=100, num_layers=1, batch_first=True)
        self.fc1 = nn.Linear(in_features=100, out_features=50)
        self.act = nn.LeakyReLU()
        self.fc2 = nn.Linear(in_features=50, out_features=1)
    
    def forward(self, x):
        # エンコーダー処理
        _, (h, c) = self.enc_lstm(x)      
        # デコーダー用の初期入力（xの最後のタイムステップ (1,2,3,4,5)なら５が入力される）
        decoder_input = x[:, -1:, 0].unsqueeze(2)  # (batch_size, 1, 1)
        # 5日目のClose価格を初期入力として使用
        #decoder_input = x[:, -1:, 3].unsqueeze(2)  # Close価格を使用
        hidden = h[-1,:,:].unsqueeze(0)
        cell   = c[-1,:,:].unsqueeze(0)
        # 予測結果を格納
        outputs = []
        # デコーダーでの予測ループ
        for t in range(dec_win_size):
            o, (hidden, cell) = self.dec_lstm(decoder_input, (hidden, cell))
            last_output = hidden[-1]      # 最後のステップの出力 o[:,-1,:]でも同じ 
            h = self.fc1(last_output)
            h = self.act(h)
            y = self.fc2(h)
            outputs.append(y)
            decoder_input = y.unsqueeze(1)  # (batch_size, 1, 1)
            
        # 予測結果を結合
        outputs = torch.cat(outputs, dim=1)
        return outputs

forwardのfor文の部分を詳しく見ていきます。入り組んでいますが、実は単純です。dec_win_sizeは教師データの窓サイズなので５です。for文はlstmとfcによる予測計算を５回繰り返すだけです。

for文の中

...
for t in range(dec_win_size):
    o, (hidden, cell) = self.dec_lstm(decoder_input, (hidden, cell))
    last_output = hidden[-1]      # 最後のステップの出力 o[:,-1,:]でも同じ 
    h = self.fc1(last_output)
    h = self.act(h)
    y = self.fc2(h)
    outputs.append(y)
    decoder_input = y.unsqueeze(1)  # (batch_size, 1, 1)
...

o, (hidden, cell) = self.dec_lstm(decoder_input, (hidden, cell))この部分の動きがポイントです。

１回目のループ
- decoder_inputは５期目の始値、hiddenとcellはデコーダーの最終出力
- lstmの出力である、hiddenかoの出力を全結合層に入力して予測値yを求めます
２回目のループ
- decoder_input=y.unsqueeze(1)つまり６期目の予測値です
- hiddenとcellはdec_lstmの出力になります
- lstmの出力を全結合層に入力して予測値yを求めます
３回目のループ
- decoder_input=y.unsqueeze(1)つまり７期目の予測値です
- hiddenとcellはdec_lstmの出力になります
- lstmの出力を全結合層に入力して予測値yを求めます
  ....
５回目のループ
- decoder_input=y.unsqueeze(1)つまり９期目の予測値です
- hiddenとcellはdec_lstmの出力になります
- lstmの出力を全結合層に入力して予測値yを求めます
outputs.append(y)で予測値を集めていきます
ところどころunsqueeze()がついているのは、データの形状を合わせるためです

forwardの部分は複雑でしたが、print(model)の結果はとてもシンプルです。

modelの構造

DNN(
  (rnn): LSTM(4, 100, batch_first=True)
  (fc1): Linear(in_features=100, out_features=50, bias=True)
  (act1): ReLU()
  (fc2): Linear(in_features=50, out_features=1, bias=True)
)

2.3 誤差関数と誤差最小化の手法の選択

回帰問題なので予測値y と実測値（教師データ）t の二乗誤差を小さくしていく方法で学習をすすめます。

# 損失関数と最適化関数の定義
criterion = nn.MSELoss() # 平均二乗誤差
optimizer = torch.optim.AdamW(model.parameters())

2.4 変数更新のループ

LOOPで指定した回数

y=model(x) で予測値を求め、
criterion(y, t_train) で指定した誤差関数を使い予測値と教師データの誤差を計算、
誤差が小さくなるようにoptimizerに従い全結合層の重みとバイアスをアップデート

を繰り返します。

学習ループ

LOOP = 5_000
model.train()
for epoch in range(LOOP):
    optimizer.zero_grad()
    y = model(x_train)
    loss = criterion(y, t_train)
    if (epoch+1)%1000 == 0:
        print(f"{epoch}\tloss: {loss.item()}")
    loss.backward()
    optimizer.step()

forループで変数を更新することになります。損失の減少を観察しながら、学習回数や学習率を適宜変更することになります。ここまでで、基本的な学習は終わりとなります。

2.5 📈 検証

2.1のデータ分割で作成したテストデータ x_test と t_test を利用して学習結果をテストしてみましょう。x_testをmodelに入れた値 y_test = model(x_test) が予測値となります。y_testは５期ごとの予測値のリストになります。表のような形になります。

	5期分の値
y_test[0]	3.83, 3.83, 3.85, 3.85, 3.85
y_test[1]	3.85, 3.85, 3.86, 3.87, 3.87
︙	︙
y_test[99]	3.85, 3.84, 3.83, 3.82, 3.82

グラフの描画ですが、5期予測して、また、次の5期を予測する形でグラフを描画してみました。5期間とばしながら予測値をプロットしていくスタイルです²。

予測値と実測値　50期まで

import matplotlib.pyplot as plt
import japanize_matplotlib


# 予測値のリスト
with torch.inference_mode():
    output = model(x_test)
y_test = output.cpu().detach().numpy()

# 実測値のリスト
# 今回はdec_win_sizeの先頭部分を集めれば実測値となる
real_list = [item[0].detach().cpu().numpy() for item in t_test]

e = 100 # period 100期分表示

plt.figure(figsize=(15,10))

plt.title(f"{dec_win_size}期先までの予測　5期ごと表示")
plt.plot(real_list[:e], label="real", marker="^")
for i in range(0,e-dec_win_size+1,5):
    plt.plot(range(i, i + len(y_test[i])), y_test[i], linestyle="dotted", label="prediction" if i == 0 else "", marker="*", color="red", alpha=0.5)
plt.legend()
plt.grid()
plt.show()

100期間を一度に表示させるとグラフが見づらいので半分に分けて作図してみました．

図：0〜49期・5期先まで予測したものをつなげたグラフ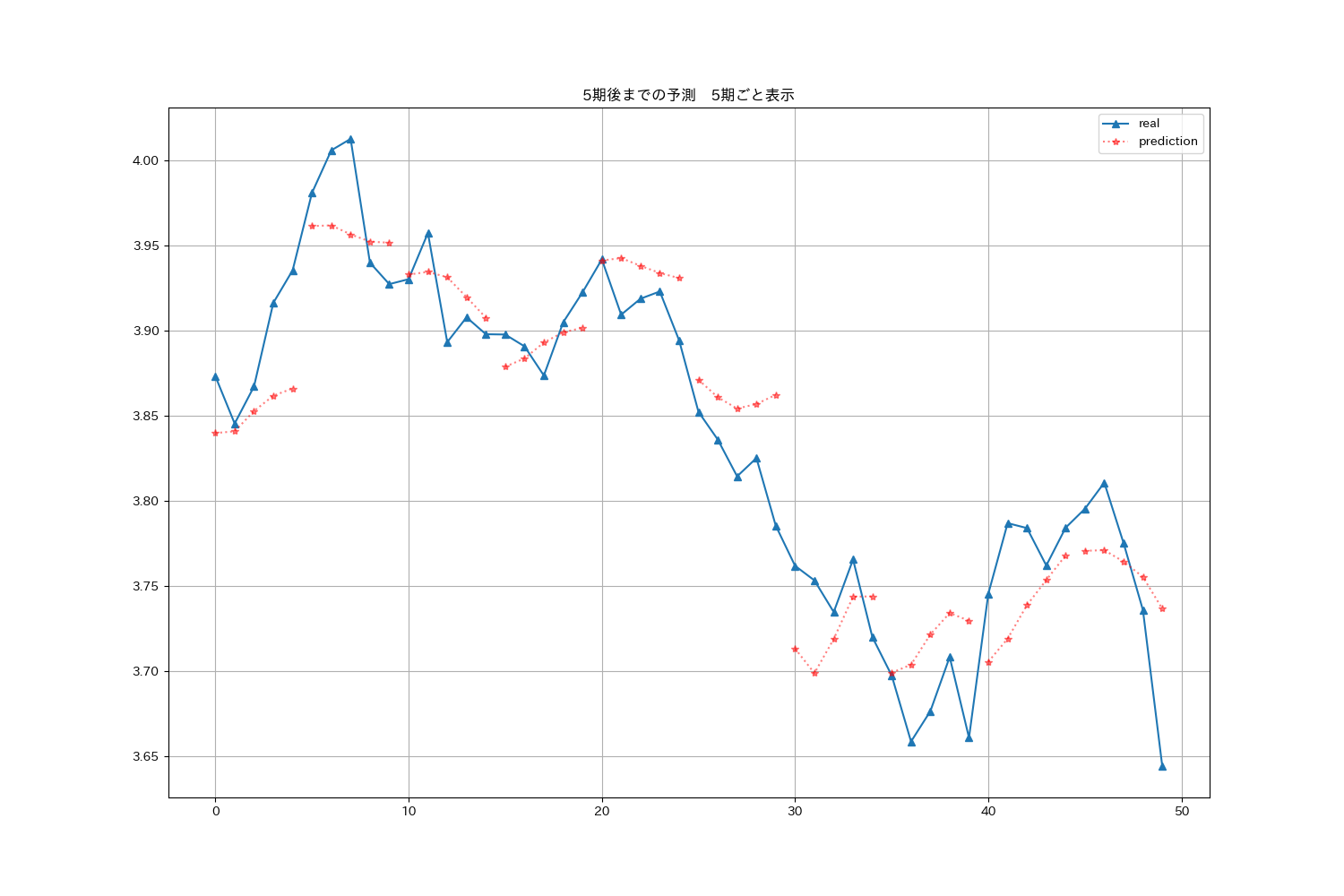

う〜ん。なにか違う気がする³。トレンドはつかめているけど、3期先の予測はほぼ役立たないな
３期先になると誤差が蓄積されているのでは？と思い、学習時に、教師強制（Teacher Forcing）の方法⁴を取り入れてみたのですが、ちょっぴり改善という程度でした。場合によっては改悪されている部分もありました

系列変換モデルにするからといって、単純なLSTMよりもモデルの性能が向上するというわけではないのがわかります。エンコーダーの形が第9回の構造と似ているしね。複数期先まで予測できるのが系列変換モデルの面白い部分なのかな。

図：50〜99期・5期先まで予測したものをつなげたグラフ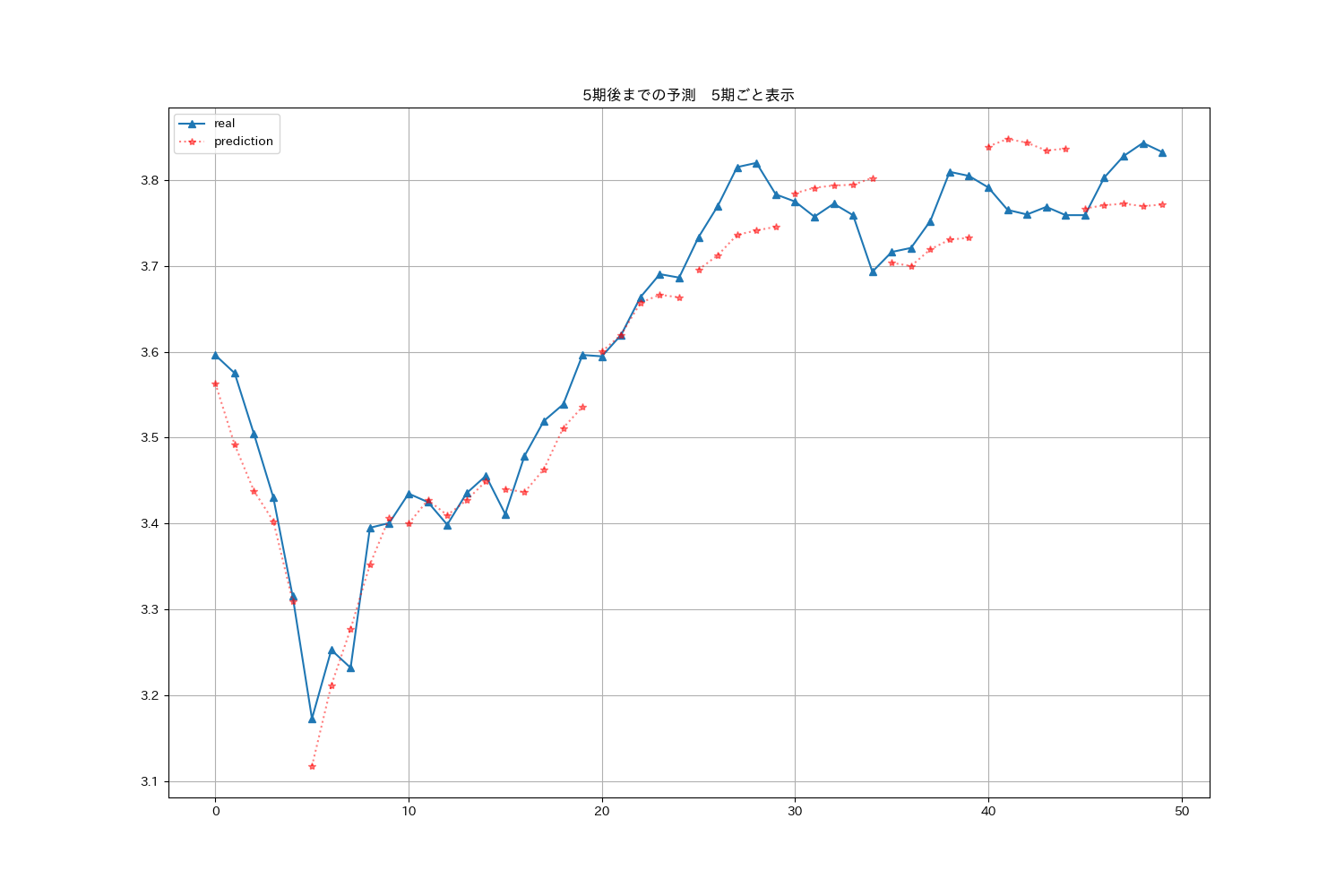

5日分の予測となるとなかなか難しい？とは思うのですが大まかな傾向が捕まえられるという意味では有用な気もします。ただし当たっていればの話ですが。50期くらいまでは上下の傾向は捉えられている気がします。50期目以降のグラフは、思いの外良い傾向にあるかな？最後の20期間はちょっと残念な結果となっています。予測はちょっと外れ気味です〜

注意機構のないLSTMの系列変換モデルでは、エンコーダーのLSTMの初期値($h_5$, $c_5$)としてしかエンコーダーの情報が利用されていません。デコーダーの情報が、エンコーダー側に伝わりきれていない可能性があります。デコーダー時にもエンコーダーの情報を積極的に参照しようという発想が注意機構を導入した系列変換モデルとなります。

RNNを利用した系列変換・エンコーダーとデコーダーモデル

Cho et al., (2014) "Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation"
Sutskever et al., (2014) "Sequence to Sequence Learning with Neural Networks"

アイディアは、もっと昔からあるようで、翻訳タスクが多いみたい。

次回

ここまできたら注意機構になるのが自然な流れのような気がしますが一旦休憩です次回は時系列分析で登場する１次元畳み込み層や因果畳み込み層について簡単に触れたいな〜

目次ページ

注

「デコーダーの最初の入力値に何を利用するのか？」６期目の始値を予測したいので、入力するデータに５期目の始値を使います。５期目の始値、高値、安値、終値の４種類を入力する場合は、デコーダーでの予測を４種類にする必要があります。この場合、デコーダーのLSTMは
self.dec_lstm = nn.LSTM(input_size=4, hidden_size=100, num_layers=1, batch_first=True)のように、４次元入力となります。合わせて、最終出力を決める全結合層も
self.fc2 = nn.Linear(in_features=50, out_features=4)のように4次元出力となります。教師データも始値、高値、安値、終値の4種類用意する必要があります。う〜ん。なかなか面倒くさい。 ↩
毎期5期ずつの予測を描画するスタイルだとグラフが極めて見にくいぞ〜 ↩
上のグラフはたまたまうまく学習できたときの様子です。損失があまり下がっていない状態だと右上がりやU字型に予測することが多かった気がします。 ↩
デコーダーでの入力値に予測値だけでなく、実際に値（教師データ）を使う方法を総称してTeacher Forcing（教師強制）と呼んでいるようです。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up