LoginSignup
3
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

AI・機械学習 Qiita Tech Festa 2025
Qiita Tech Festa20252025年7月15日まで開催中！
@AzukiImo

🔰PyTorchでニューラルネットワーク基礎 #08 【再帰ネットワーク・LSTM】

Last updated at Posted at 2025-07-01

概要

個人的な備忘録を兼ねたPyTorchの基本的な解説とまとめです。第８回は再帰ネットワークのLSTMを利用した日経225を利用した予測となります。再帰ネットワークの初回なので、次の日の日経225の始値を予測する単純な形から始めます。次の日の値を予測するスタイルなので回帰分析の延長線上になります．

第2回の回帰問題からの追加箇所は大きく１箇所で、再帰ネットワークのLSTMを使う部分になります。

方針

  1. できるだけ同じコード進行
  2. できるだけ簡潔（細かい内容は割愛）
  3. 特徴量などの部分，あえて数値で記入（どのように変わるかがわかりやすい）

演習用のファイル

1. 再帰ネットワーク

$t-1$期までの過去の情報の特徴量である履歴$h_{t-1}$とその時点でのデータ$x_t$をあわせて全結合層＋活性化関数のtanhによって、$t$期までの情報の特徴量を導出していくのが再帰ネットワークの基本的な動きになります。
$$h_t=\tanh(W_x x_t + W_h h_{t-1} + b)$$

この式の重要なポイントは、同じ計算を繰り返し適用することです。

  • $x_t$：時刻$t$での新しい入力データ
  • $h_{t-1}$：前の時刻で計算した結果（これが「過去の情報」）
  • $h_t$：現在計算している結果（これが次の時刻では過去の情報・履歴の$h_{t-1}$となる）

つまり、前回の計算結果を今回の計算に使い、その結果をまた次回に使う、という循環的な構造が「再帰」となります。これにより、遠い過去の情報も段階的に現在の計算に影響を与えることができます。

PyTorchによるプログラムの流れを確認します。基本的に下記の５つの流れとなります。Juypyter Labなどで実際に入力しながら進めるのがオススメ

  1. データの読み込みとtorchテンソルへの変換　(2.1)
  2. ネットワークモデルの定義と作成　(2.2)
  3. 誤差関数と誤差最小化の手法の選択　(2.3)
  4. 変数更新のループ　(2.4)
  5. 検証　(2.5)

2. コードと解説

2.0 💹 データについて

日経225のデータをyfinanceやpandas_datareaderなどで取得します。2021年1月から2025年6月中旬頃のデータを利用しています。

Date Open High Low Close Volume
2021-01-04 27575.57 27602.11 27042.32 27258.38 51500000
2021-01-05 27151.38 27279.78 27073.46 27158.63 55000000
2021-01-06 27102.85 27196.40 27002.18 27055.94 72700000
… … … … … …
2025-06-18 38364.16 38885.15 38364.16 38885.15 110000000
2025-06-19 38858.52 38870.55 38488.34 38488.34 89300000

始値(Open)を予測する形で演習を進めていきます1。始値のグラフを描画してみましょう。青色の線が日経225の始値の折れ線グラフとなります。

nikkei225_test.jpg

学習用データとテスト用データに分割します。グラフの赤い線の右側100期をテスト用のデータとして使います。残りの左側を学習用のデータとします。学習用データで学習させて、「右側の100期間を予測できるのか？」が主目標となります。

2021年以降の日経225の値は、3万円前後の数値になることがほとんどです。誤差計算時の損失の値が大きくなりすぎないように、変数の更新がうまく行われるように、「1万円で割り算して数値を小さく」 しておきます2。これで、ほとんどの値が2.5〜4に収まるはずです。

2.1 データの読み込みとtorchテンソルへの変換

CSVファイルをpandasで読み込み、RNNで学習できる形にデータを前処理します。具体的には、株価の始値データを「窓（window）」と呼ばれる一定期間でデータを区切って、その窓を1つずつスライドさせながらデータセットを作成していきます3。

前処理の概要

次のような時系列データがあるとします。「過去の5日間のデータから翌日の値を予測する」というモデルを作成したいとしましょう。過去の５日間を窓と呼びます。窓を右に向かって移動（stride）させながら５日毎に区切っていく作業が前処理となります。

日付 Day 1 Day 2 Day 3 Day 4 Day 5 Day 6 Day 7 Day 8 ...
株価 100 102 105 103 106 108 107 109 ...

窓サイズを５、移動サイズを１とすると、完成するデータセットは下記の表の様な入力データと教師データの形になります。

開始〜終了 入力データ 教師データ 教師データの日付
Day1〜Day5 100, 102, 105, 103, 106 108 Day 6
Day2〜Day6 102, 105, 103, 106, 108 107 Day 7
Day3〜Day7 105, 103, 106, 108, 107 109 Day 8
Day4〜Day8 103, 106, 108, 107, 109 ... Day 9

元の1つの長い時系列データから、窓サイズで区切られた入力データとそれに対応する教師データが作成されます。時系列分析のテキストによると窓のサイズや移動量を適切に設定して、様々な時系列予測・分類タスクに対応するようです。

CSVファイルの読み込みから窓サイズでの分割までのコードです。

データの読み込みと前処理
import pandas as pd
import numpy as np
import torch
import torch.nn as nn

# CSVファイルの読み込み
data = pd.read_csv("./data/nikkei_225.csv")

scaling_factor = 10_000
x_open = data["Open"]/scaling_factor
# 窓で分割（前処理）
win_size = 5
XO = [x_open[start:start+win_size] for start in range(len(data)-win_size)]
T = x_open[win_size:]

pandasで読み込んだ始値のdata["Open"]をscaling_factor=10_000で割り算します。入力データの値がある程度小さくなり、学習の安定性と効率性の向上が見込めます。

５日分を窓サイズとして前処理を行います。始値であるx_openをwin_sizeで区切りつつ、移動させれば良いので、表のような形でリストに集めていきます。

５個区切り 教師データ
1個目 x_open[0:0+win_size] x_open[5]
2個目 x_open[1:1+win_size] x_open[6]
3個目 x_open[2:2+win_size] x_open[7]
︙ ︙ ︙

集まった５個区切りデータのリストをXO、教師データのリストをTとします。実際に表示するとわかるのですが、上記のコードだとXOやTはタイプが乱れている形になります:bow:

最終的にtorch.FloatTensor()の形になればよいので、今回はXOやTを一旦numpy配列に変換してからtorch.Tensorにする力技となります。

torchテンソルへ変換
# 一旦numpyへ変換する
xo = np.array(XO)
t  = np.array(T)
x = xo.reshape(xo.shape[0], xo.shape[1], 1)  # (バッチサイズ, 5, 1)
# torch.FloatTensorへ変換
# 今回からGPU使えるときはGPUを利用、それ以外だとCPUになるような設定にします
device = "cuda" if torch.cuda.is_available() else "cpu"
x = torch.FloatTensor(x).to(device)
t = torch.FloatTensor(t).to(device).view(-1,1)  # 回帰問題なので(バッチサイズ, 1)

ランダムにデータを分割する時は、scikit-learnのtrain_test_splitが役立ちます。今回のような時系列データで前半部分を学習用、後半部分をテスト用と前後に分割するだけなら、スライシングを使って手動で分割するのが簡単です。

学習用とテスト用に分割
period = 100
x_train = x[:-period]
x_test = x[-period:]
t_train = t[:-period]
t_test = t[-period:]

# 入力する特徴量は１次元
# x_train.shape : torch.size([987, 5, 1])
# x_test.shape :  torch.Size([100, 5, 1])
# t_train.shape : torch.Size([987, 1])
# t_test.shape :  torch.Size([100, 1])

2.2 ネットワークモデルの定義と作成

今回は下図のようなLSTMと全結合層を利用したネットワークで時系列予測を扱っていきます。入力データは窓サイズ５の日経225データです。（x1, x2, x3, x4, x5）と表記された５日分の始値がx1から順番に入力されます。対応する出力が（h1, h2, h3, h4, h5）となります。最終的な出力であるh5が、過去の５日分の情報を再帰的に考慮した特徴量になります。特徴量h5から全結合層を経由して最終的に翌日の予測値 y が計算されます。

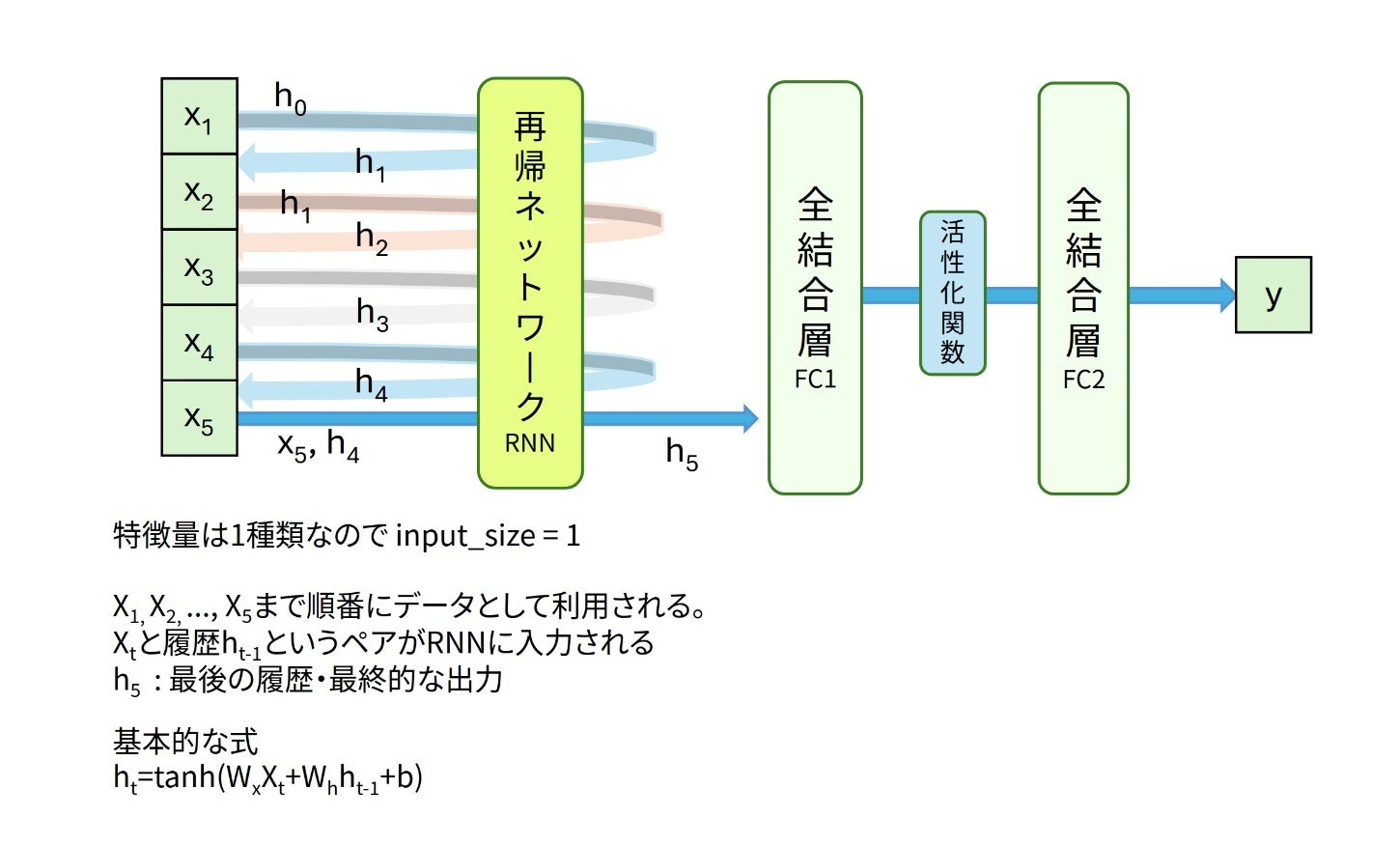
全結合層だと（x1, x2, x3, x4, x5）という5つのデータを一度に入力するので入力する特徴量はin_features=5となります。再帰ネットワークの場合は、x1, x2, x3, x4, x5 が先頭から順番に一つずつ入力されるので、input_size=1と指定すること要注意です。

PyTorchの再帰ネットワークには、RNN、LSTM、GRUが用意されています。どれも同じような引数をもちます。LSTMを代表として書き方のポイントをまとめておきます。

LSTM層の書き方
nn.LSTM(input_size, hidden_size, num_layers, batch_first)

  • input_size : 入力される特徴量の次元
  • hidden_size : 出力される隠れ層の特徴量の次元
  • num_layers :　再帰するLSTMの数、デフォルトはnum_layers=1。
  • batch_first : Trueで（バッチサイズ、系列長、特徴量）の形状 になる。デフォルトは歴史的な経緯？からFalseで（系列長、バッチサイズ、特徴量）になり注意！

詳細はPyTorchの公式ドキュメントに記載されています。

batch_first=Trueと指定して、バッチサイズの先頭に固定することでコードがスッキリします:smile: batch_firstのT/Fで出力の形状や意味が変わります。要注意ポイントとなります。

LSTMの出力に注意。batch_first=Trueのlstm(x)の出力値は３種類。
o, (h, c) = lstm(x)

  • o : すべての時点での最終層（一番最後layer）の隠れ状態の出力
  • h : 最後の時点でのすべての隠れ層の出力
  • c : 最後の時点におけるセル状態

oとhの違いは言葉だと難しいので、視覚的にイメージしてみました。num_layers=3の例となります。$h_{35}$を次の入力に使います。

num_layers=3でのoとh
Day:    x1    x2    x3    x4    x5
層3:    h31   h32   h33   h34   h35  ← oに含まれる[h31, h32, h33, h34, h35] 
層2:    h21   h22   h23   h24   h25
層1:    h11   h12   h13   h14   h15
                               ↑
                            hに含まれる
                          [h15, h25, h35]

上図の「LSTM→全結合層→全結合層」のモデルのネットワーク構造を記述していきます。

モデル定義
class DNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.rnn  = nn.LSTM(input_size=1 ,hidden_size=100, num_layers=1, batch_first=True)
        self.fc1 = nn.Linear(100, 50)
        self.act1 = nn.ReLU()
        self.fc2 = nn.Linear(50, 1)

    def forward(self, x):
        o, (h, c)  = self.rnn(x)
        last_output = h[-1]      # 最後のステップの出力 o[:,-1,:]でも同じ 
        h = self.fc1(last_output)
        h = self.act1(h)
        y = self.fc2(h)
        return y

model = DNN()
model.to(device)

print(model)の結果はとてもシンプルです。

modelの構造
DNN(
  (rnn): LSTM(1, 100, batch_first=True)
  (fc1): Linear(in_features=100, out_features=50, bias=True)
  (act1): ReLU()
  (fc2): Linear(in_features=50, out_features=1, bias=True)
)

2.3 誤差関数と誤差最小化の手法の選択

回帰問題なので予測値y と実測値（教師データ）t の二乗誤差を最小にする方法で学習をすすめます。

# 損失関数と最適化関数の定義
criterion = nn.MSELoss()
optimizer = torch.optim.AdamW(model.parameters())

2.4 変数更新のループ

LOOPで指定した回数

  1. y=model(x) で予測値を求め、
  2. criterion(y, t_train) で指定した誤差関数を使い予測値と教師データの誤差を計算、
  3. 誤差が小さくなるようにoptimizerに従い全結合層の重みとバイアスをアップデート

を繰り返します。

学習ループ
LOOP = 8_000
model.train()

for epoch in range(LOOP):
    optimizer.zero_grad()
    y = model(x_train)
    loss = criterion(y,t_train)           # 平均二乗誤差
    if (epoch+1)%500 == 0:
        print(epoch,"\tloss:", loss.item())#, "\tR2:",r2.item())
    loss.backward()           # 逆伝播微分
    optimizer.step()          # パラメータ更新

forループで変数を更新することになります。損失の減少を観察しながら、学習回数や学習率を適宜変更することになります。ここまでで、基本的な学習は終わりとなります。

2.5 📈 検証

2.1のデータ分割で作成したテストデータ x_test と t_test を利用して学習結果をテストしてみましょう。x_testをmodelに入れた値 y_test = model(x_test) が予測値となります。グラフを利用して視覚的に検証！

テストデータでの検証「最後の100期」_1dim_lstm.png

きれいに1期ずれた予測になっています。緑色の線を学習したかのようなシンクロ率:sweat_smile::smile::sweat_smile:

予測値と実測値の可視化
import matplotlib.pyplot as plt
import japanize_matplotlib

model.eval()
y_test = model(x_test)

prediction = y_test.detach().cpu().numpy()
real = t_test.detach().cpu().numpy()

# 一つ前の期の実測値も示したい
e = period

plt.figure(figsize=(15,8))
plt.plot(real[1:e], label="real", marker="^")
plt.plot(prediction[1:e], label="prediction", linestyle="dotted", marker="*")
plt.plot(real[:e-1], label="１期ずれ", marker="+")
plt.legend()
plt.title(f"テストデータでの検証「最後の{period}期」")
plt.show()

１期前の実測値のグラフもplt.plot(real[:e-1], label="１期ずれ", marker="+")として表示しました。周期性のない時系列データをRNNで予測させると、１期ずれた、ラグのある状態に近くなることが多く観察されるようです。理由は詳しくないのですが、１期前の値を利用した予測（ナイーブ予測）だとある程度誤差が抑えられるようになるのかと勝手に推測しております:sweat_smile:　感覚的には、「今日の状態が明日も続くと予想しておけば、大きく外れることはない！」という発想なんでしょうか:open_mouth::fearful::scream:

次回

さすがに、１期ずれた状態で終わるのも良くないので、次回はナイーブ予測である「今日の状態が明日も続く」とはならない結果を目標してみたいと思います4。複数期先の予測にも挑戦したい:airplane:

LSTMと株価予測の参考サイト

再帰ネットワークを利用した株価の予測はたくさん解説されています。いくつか紹介しておきます。

目次ページ

注

  1. その日の取引結果を最もよく反映しているという点で終値を利用することが多いです。時系列と再帰ネットワーク演習ですので、高値・安値・取引量など好きな値で試してください。高値と安値の予測値で実測値を挟み込めれば、それも意味あるかな？:airplane: ↩

  2. 実際に試してみるとわかるのですが、学習データの値が大きすぎると、学習が不安定になったり、学習が全く進まないというが起こり得ます。データをある程度の範囲にきれいに収める正規化と呼ばれる格好良い手法があります。今回は割り算で対応してみました。単位が万円という意味合いで解釈も容易ですし:palm_tree::sweat_smile::palm_tree:　 ↩

  3. numpyでCSVやNPZファイルを読み込んでtorch.Tensorではなく、ひと手間かかります:bow: ↩

  4. おそらく数値的にみて改善できる予定です:sweat_smile: ↩

3
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?