1
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@AzukiImo

🔰PyTorchでニューラルネットワーク基礎 #21 【文章分類・Conv1d】

Posted at

概要

個人的な備忘録を兼ねたPyTorchの基本的な解説とまとめです。今回はテキスト分類問題の2回目となります。第20回【CNNによるテキスト分類】に引き続き90個のテキスト分類データを利用して演習を行っていきます。

分類イラスト.png

文章は前から順番に読んで理解しているはず。つまり、文章は時系列として扱うことができます。この構造を利用して1次元畳み込みによる方法で文章分類を行ってみたいと思います。

Yoon Kim (2014) Convolutional Neural Networks for Sentence Classification に登場するネットワーク構造を参考に実装してみたいと思います。

textCNN.png
図１：テキストCNN

論文のFigure １だと、埋め込み層の重みを更新するタイプ(non-static)と更新しないタイプ(static)の２つを使いますが、今回はnon-staticのみでモデルを記述していきます。構造がスッキリします。事前学習した重みがないというのも主たる原因なのですが:bow::bow::bow:

どちらかというと、第13回の音楽ジャンル分類に近い構造になります。

方針

  1. できるだけ同じコード進行
  2. できるだけ簡潔（細かい内容は割愛）
  3. 特徴量などの部分，あえて数値で記入（どのように変わるかがわかりやすい）

演習用のファイル

データファイルdata_90.zipを解凍してから演習に利用してください。解凍すると以下の5種類になります。

  • nlc_data_90.csv：テキスト分類のデータ
  • x_id_vector.csv：IDベクトル（入力データ）
  • y_labels.csv：ラベルデータ
  • id_dic.txt：単語とIDの対応表
  • id2word_dic.pickle：idから単語への辞書

1. テキスト分類と1次元畳み込み

画像分類に代表される分類問題はデータをカテゴリー・クラスに振り分ける問題となります。テキスト分類も同様で、アンケートの自由回答欄や商品レビューを「好意的、中立的、否定的」に分けるような場合に利用できそうです。

PyTorchによるプログラムの流れを確認します。基本的に下記の５つの流れとなります。Juypyter Labなどで実際に入力しながら進めるのがオススメ

  1. データの読み込みとtorchテンソルへの変換　(2.1)
  2. ネットワークモデルの定義と作成　(2.2)
  3. 誤差関数と誤差最小化の手法の選択　(2.3)
  4. 変数更新のループ　(2.4)
  5. 検証　(2.5)

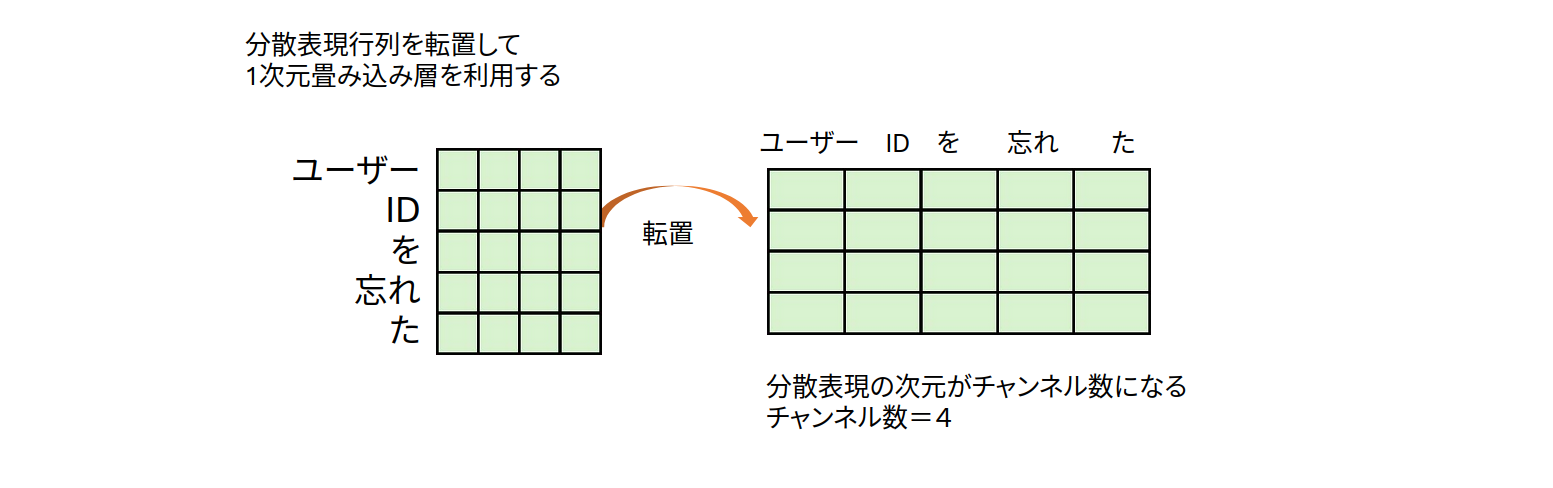
テキストデータは第19回【単語の分散表現】で演習したようにIDベクトル化（トークナイズ）したあと、埋め込み層を利用して、分散表現の行列の形で表現できることがわかっています。分散表現行列を転置して、分散表現の次元をチャンネル数とみなせば テキストデータも音声データや株価などの時系列データと類似の構造になります。図２のように列に単語が並ぶ形になれば1次元畳み込みをうまく利用できそうです。

wv_transpose.png
図２：分散表現行列とその転置

2. コードと解説

2.0 データについて

利用するデータについて簡単に紹介します。ある架空のwebサービスを利用する場面を想定しています。利用サービスに関するテキスト分類で、「ログインに関する内容」、「登録に関する内容」、「解約に関する内容」の３種類のカテゴリーで分類するものとなります。文章を演習用に短文化するため句点も省略して<bos>で代用しています。具体的には、次のような形になります。

文章 分類名
ログインできない ログイン
入会したい 登録
退会したい 解約

MeCabなどで形態素解析を行い、単語IDの辞書を作成します。4種類のタグを準備しました。<unk> は辞書にない単語、<bos>は文の開始記号、<eos> は文の終端記号、<pad>は文の長さを調整する記号をそれぞれ表しています。

単語ID辞書のサンプル
<unk> : 0
<bos> : 1
<eos> : 2
<pad> : 3
ID:4
︙
ログイン:67
︙

辞書を利用して、文章をIDベクトルで表現します。データの形を固定するために、<pad>を用いて文を同じ長さを等しくします。

等長化した文のIDベクトルは次のようになります。分類IDは分類名を番号で記したものです。

文章 IDベクトル 分類名 分類ID
ログインできない 1,67,67,19,24,2,3,3,3,3,3,3 ログイン 1
入会したい 1,86,11,16,2,3,3,3,3,3,3 登録 2
退会したい 1,141,11,16,2,3,3,3,3,3,3 解約 0

等長化されたIDベクトルが入力データ、分類IDが教師データとなります。

2.1 データの読み込みとtorchテンソルへの変換

まず利用するライブラリを読み込みます。

ライブラリ
import numpy as np
import torch
import torch.nn as nn
from sklearn.model_selection import train_test_split

データの読み込み

$x$ がIDベクトルになった文、$t$ が分類IDで０，１，２という整数値の教師データです。scikit-learnのtrain_test_splitを利用して、学習に利用するデータとテスト（検証）に利用するデータに分割します。

データの読み込み
# (1) デバイスの選択
device = 'cuda' if torch.cuda.is_available() else 'cpu'
print("利用デバイス:", device)

# (2) データの読み込み
# x: IDベクトル（文）
# t: ラベル（0, 1, 2）
# torchテンソルに変換
x = np.loadtxt("data_90/x_id_vector.csv", delimiter=",")
t = np.loadtxt("data_90/y_labels.csv", delimiter=",")
x = torch.LongTensor(x)
t = torch.LongTensor(t)

# (3) 学習用データと検証用データに分割
x, x_test, t, t_test = train_test_split(x,t, stratify=t,  random_state=55)

# (4) GPU使える場合はGPUへ
x = x.to(device)
t = t.to(device)
x_test = x_test.to(device)
t_test = t_test.to(device)

# x.shape: torch.Size([67, 11]) 
# x_test.shape: torch.Size([23, 11])

説明メモ

  • (1) 利用するデバイスの設定。GPUあるときは使うぞ。
  • (2) np.loadtxt(ファイル名，句切り記号)を利用してCSVファイルを読み込みます。
  • 入力データも教師データも整数なので、torch.LongTensor()を使います。
  • (3) train_test_splitのオプション stragify=t を指定すると、学習用データと検証用データで分類IDの比率を元のデータと同じに保つように分割できます。tと同じような割合で分割という意味です。

2.2 ネットワークモデルの定義と作成

今回は下図のようなConv1d（１次元畳み込み）と分類のための全結合層を利用したネットワークで分類問題を扱ってみたいと思います1。畳み込みで抽出した特徴量をつなげて、全結合層により３次元ベクトル（３種類の予測）を出力する形となります。

text_cnn_type.png
図３：ネットワーク構造

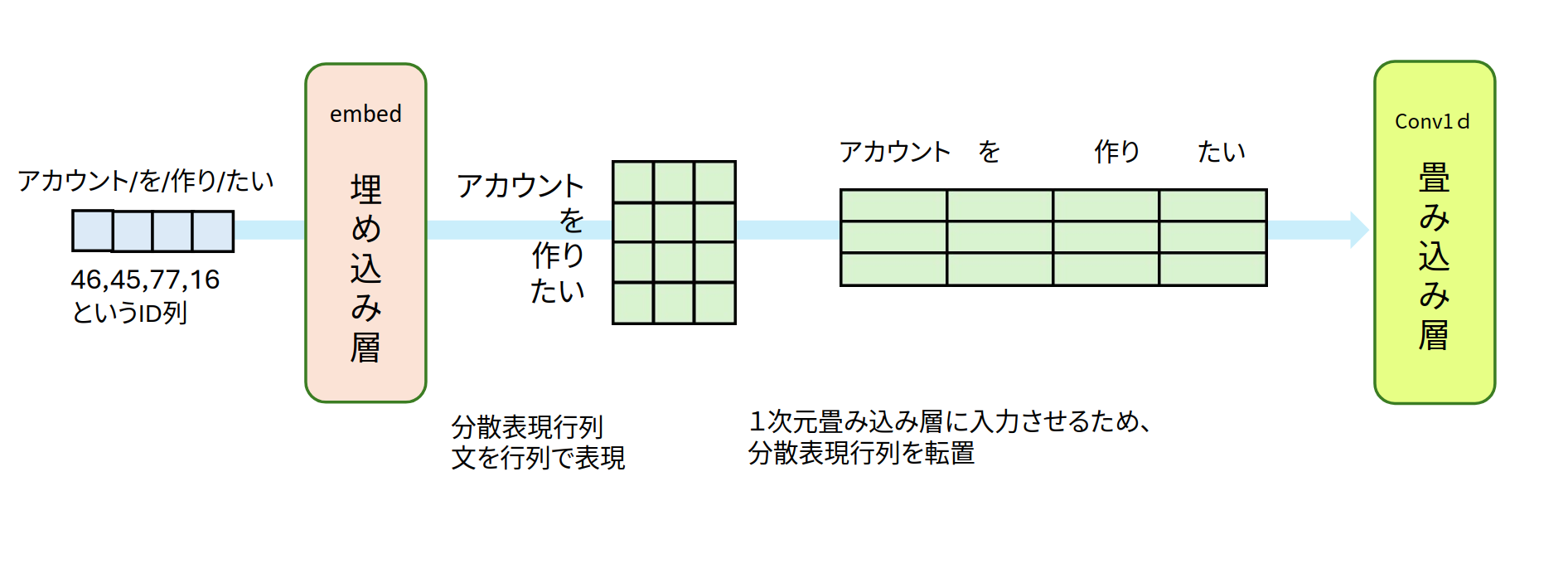
  • 入力するデータは「アカウントを作りたい」をIDベクトル化した整数値のベクトルです。
  • 埋め込み層によって、分散表現行列（系列長×分散表現の次元）の形になります。
  • 転置した分散行列を１次元畳み込み層へ入力します。図３はカーネルサイズ違いの３種類のConv1dへ、分散表現行列を入力しています。上から順番にカーネルサイズ３，４，５となります。見た目は並列的な流れになります。
  • Conv1dから求められる特徴量をAdaptiveMaxPool1dで列ベクトルの形に整えます。すべてのConv1dの出力が同一の形になります。図３だと３次元ベクトルになっています。
  • 3種類の特徴量を全部つなげて、全結合層の入力とします。図３では９次元ベクトルになります。
  • 最後に全結合層の出力と分類数を比較する形になります。

基本的な確認事項

  • WORDS = 146 # 単語数　作成した辞書から数を求める
  • SEQ_LEN = 11 # 入力するIDベクトルの長さ x.shape[1]
  • CLASSES = 3 # 分類数

ネットワークの書き方はこれまで同様にクラスを利用して記述します。
(1) __init__() ： 利用するネットワーク名・活性化関数をすべて記述
(2) forward() ： 実際の流れを記す

2.2.1. 1次元畳み込みとプーリング層をまとめたネットワーク層

1次元畳み込みとプーリング層のパターンを何度か利用するのでひとまとめにしてCNN1Dクラスを作成する方向で実装してみました。Conv1dやAdaptiveMaxPool1dの基本的な解説は、第12回【Conv1d】を参考にしてください。

最終的なネットワークはCNN1Dを利用して記述することになります。

1次元畳み込みとプーリング層をまとめたネットワーク層
class CNN1D(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, padding="same"):
        super().__init__()
        # １次元畳み込み層 -> プーリング層 -> (バッチサイズ, 特徴量ベクトル)
        self.conv = nn.Conv1d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, padding="same")
        self.bn   = nn.BatchNorm1d(out_channels)
        self.act  = nn.ReLU()
        # プーリング・Dropout・全結合など追加すると本格的
        self.pool = nn.AdaptiveMaxPool1d(1)

    def forward(self, x):
        h = self.conv(x)
        h = self.bn(h)                     
        h = self.act(h)
        y = self.pool(h).squeeze(-1)        # (B, 特徴量ベクトル)
        return y

説明メモ

  • 1次元畳み込み層とプーリング層の部分をひとまとめとするブロックにしてみた。
  • CNN1Dによってkernel_sizeごとにネットワーク層を作りやすくなるぞ〜。
  • AdaptiveMaxPool1d(1)とすることで、特徴量はベクトルの形になります。
  • 出力値を（バッチサイズ，特徴量ベクトル）に変更している点に注意。

それぞれの部分を詳しく見ていきます。

2.2.2. 埋め込み層と転置

埋め込み層によって文を分散表現行列に変換し、（系列長，分散表現の次元）の行列の形とします。図４では、４つの単語からなる文を３次元に埋め込んだ行列として描いています。この行列を１次元畳み込みへ入力するために、転置して縦横を入れ替え、（分散表現の次元，系列長）の形にします。分散表現の次元がチャンネル数になります。図４だと３チャンネルになるので、Conv1d(in_channels=3,...)となります。

transpose.png
図４：埋め込み層からConv1dへの入力まで

2.2.3. １次元畳み込み層への入力と出力

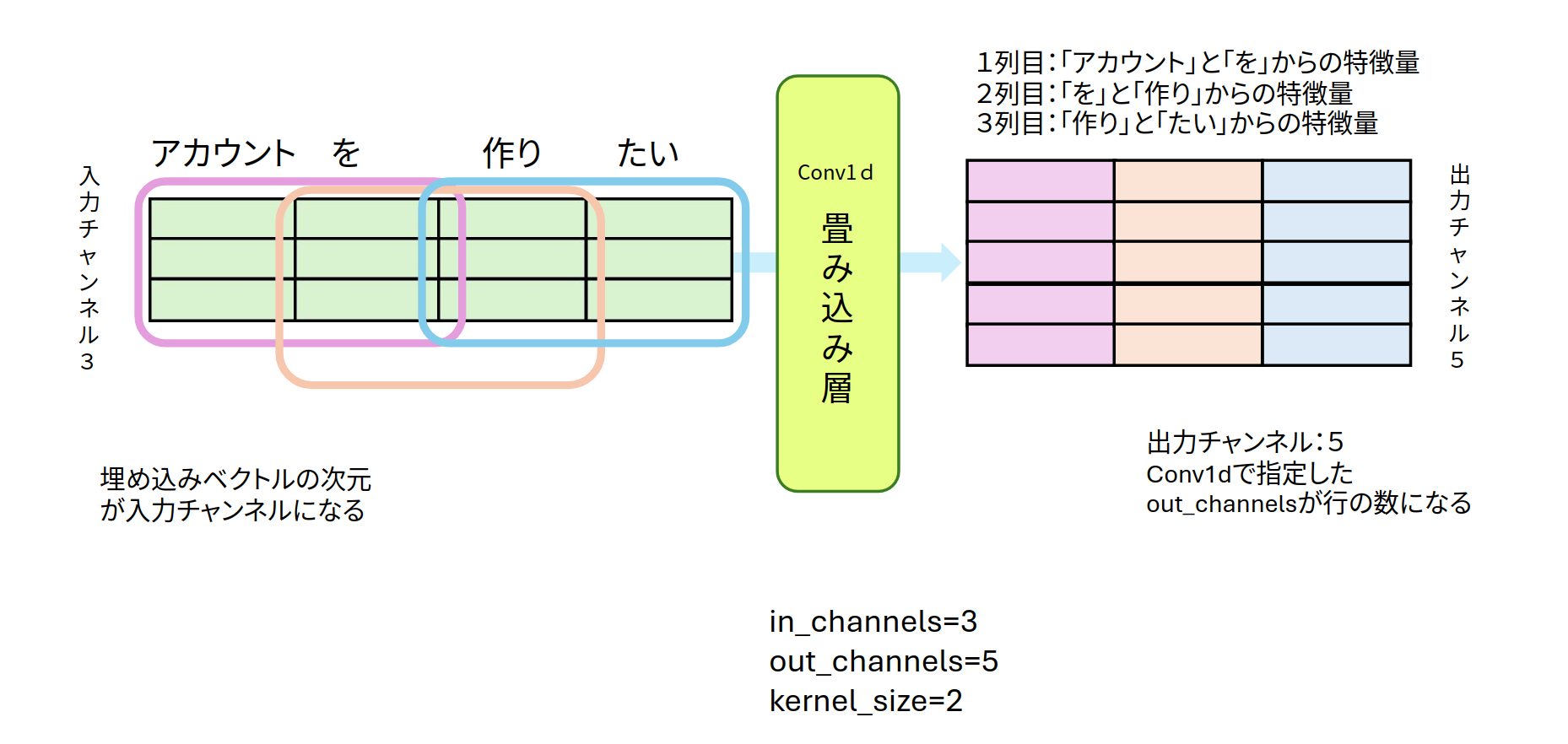
１次元畳み込み層への入力データは、（チャンネル数、系列長）の形を取ります。下の図のように分散表現行列を転置した横方向に単語が並ぶ形が１次元畳み込みへの入力データとなります。

conv1d.png
図５：Conv1dの入出力

分散表現ベクトルを入力チャンネルとみなして、Conv1dを適用します。図５は in_channels=3 で kernel_size=2、out_channels=5です。前後の単語関係の特徴を考慮しながら、５種類のカーネルで特徴量を求めているのが図５となります。Conv1dの出力結果は５×３の形になります。

2.2.4. AdaptiveMaxPool1d()の出力

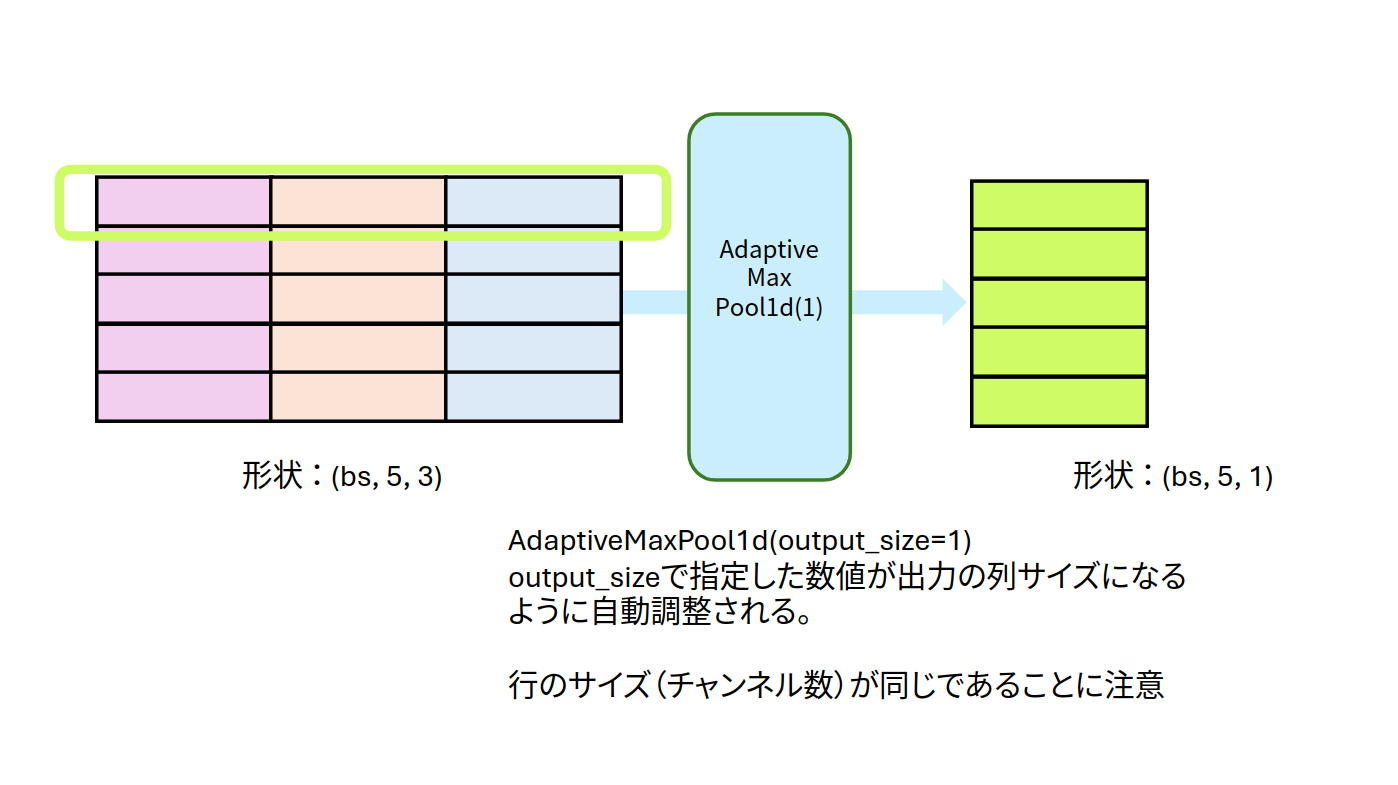
１次元畳み込みによって抽出した特徴量（5×3）に対して、１次元最大プーリングを使ってみます。出力の列サイズを指定できるAdaptiveMaxPool1d(output_size=1)のoutput_sizeオプションを利用して、５×３の特徴量から５×１の列ベクトルの形を抽出したものが図となります。

adaptive_pool.png
図６：AdaptiveMaxPool1dの入出力

CNN1Dクラスは、Conv1dとAdaptiveMaxPool1dの２つを軸に構成したネットワーク構造です。出力値を全結合層で変換するために、列ベクトルを行ベクトルに並び替えする調整を加えてCNN1Dの出力とします。

CNN1Dクラスのkernel sizeを利用して、３単語、４単語、５単語の関連度を求め、文章から特徴量を抽出したネットワークを作成していきます。

ネットワークモデルの定義と作成
class DNN(nn.Module):
    def __init__(self):
        super().__init__()

        self.embed = nn.Embedding(num_embeddings=WORDS, embedding_dim=10)
        self.cnn3  = CNN1D(in_channels=10, out_channels=16, kernel_size=3, padding="same")
        self.cnn4  = CNN1D(in_channels=10, out_channels=16, kernel_size=4, padding="same")
        self.cnn5  = CNN1D(in_channels=10, out_channels=16, kernel_size=5, padding="same")
        self.fc = nn.Linear(16 * 3, 3) # in_features = 特徴量×3 : ３は畳み込み層の数

    def forward(self, x):                     # x: (B, L)　B:バッチサイズ, L:系列長, E:埋め込み次元
        h = self.embed(x)                     # (B, L, E)
        # (1) 【重要】転置して、横に単語が時系列順に並ぶ形にする
        h = h.permute(0, 2, 1)                # (B, E, L) 転置 conv1dの入力
        # (2) カーネルサイズで分岐
        h3 = self.cnn3(h)   # kernel_size=3 で特徴量抽出
        h4 = self.cnn3(h)   # kernel_size=4 で特徴量抽出
        h5 = self.cnn3(h)   # kernel_size=5 で特徴量抽出

       # (3) 特徴量を結合
        v = torch.cat([h3, h4, h5], dim=1)        # (B, 3×特徴量ベクトル)
        y = self.fc(v)
        return y

model = DNN()
model.to(device)

説明メモ

  • nn.Sequential()やnn.ModuleList()を使わずにベタにネットワーク層を書いてみました。
  • (1) 転置（くどい:bow:）
  • (2) カーネルサイズでネットワークが分岐します。一旦３種類に別れます。
  • (3) それぞれのCNN1Dで抽出した特徴量を結合して分類の全結合へ入力します。図３の３×１の3種類の特徴量をひとまとめにする部分に相当します。

2.3 誤差関数と誤差最小化の手法の選択

分類問題なのでおなじみのCrossEntropyLoss()を使います。

criterion = nn.CrossEntropyLoss()                           # 損失関数：cross_entropy
optimizer = torch.optim.AdamW(model.parameters(), lr=0.01)  # 学習率：lr=0.001がデフォルト
  • nn.CrossEntropyLoss() は予測値と実測値（教師データ）のクロスエントロピー損失。使用時は、criterion(x,t) とする。
  • torch.optim.AdamW() は誤差の最小値を求める方法の一つです。学習率は適宜変更してください。

2.4 変数更新のループ

LOOPで指定した回数、

  1. y=model(x) で予測値を求め、
  2. criterion(y, t) で指定した誤差関数を使い予測値と教師データの誤差を計算、
  3. 誤差が小さくなるようにoptimizerに従い全結合層の重みとバイアスをアップデートします。
LOOP = 50

for epoch in range(LOOP):
    optimizer.zero_grad()
    y = model(x)
    loss = criterion(y, t)
    acc  = accuracy(y,t)
    loss.backward()
    optimizer.step()    
    print(f"{epoch}:\tloss:{loss.item():.3f}\tacc:{acc:.3f}")

平均精度について

予測値と教師データで等しい値なら正解として、正解数/問題数で精度を求める単純な平均精度を求める作成してみました。

accuracy関数
def accuracy(y, t):
    _,argmax_list = torch.max(y, dim=1)
    accuracy = sum(argmax_list == t).item()/len(t)
    return accuracy

2.5 検証

2.1のデータ分割で作成したテストデータ x_test と t_test を利用して学習結果をテストしてみましょう。x_testをmodelに入れた値 y_test = model(x_test) が予測値となります。accuracyで平均精度を求めれば完成です。

検証
model.eval()
y_test = model(x_test)
acc = accuracy(y_test, t_test)
print(f"検証精度: {acc}")
# 検証精度: 0.8695652173913043

平均精度87%:sweat:　たまたまの結果。ちなみに、87%は運の良い結果です。ほとんど70〜80%くらいだと思います。第20回CNNでのテキスト分類での検証精度はデータ数が60個の場合50%前後、90個の場合70％前後でした。

  • 複数のカーネルサイズを利用している点

これが精度向上に貢献していると考えられます。

地味に一つずつ確認して表にまとめてみました。本当は「解約」の内容なのに「ログイン」や「登録」と誤判定していることが伺えます。

                  予測値     
                  解約 ログイン 登録
実際の値　解約　　　　6    1      1
　　　　　ログイン　　1    7      0
　　　　　登録　　　　0    0      7

次回

次回、文章といえばTransformer。ということでTransformer Encoderを利用したテキスト分類いわゆるBERT風のネットワークを扱う予定です。

目次ページ

注

  1. ネットワークの画像って作成者しかわからないということがよくある。 ↩

1
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?