【非線形の分位点回帰】　楽観的予測〜悲観的予測

Posted at 2025-09-09

概要

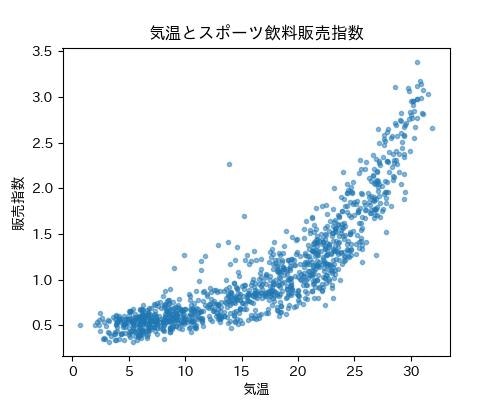
回帰分析といえば線形が定番です。前回利用した平均気温とスポーツ飲料の販売指数の散布図（下のグラフ）、線形よりも二次関数っぽく見えませんか

非線形回帰は係数の解釈などやや難しい面もありますが。グラフの形状から二次関数や指数関数を使ったほうが、線形モデルよりもフィットしそうな予感ということで、今回は二次関数や指数関数を利用した非線形な分位点回帰の演習を行ってみたいと思います¹。

方針

statsmodelsライブラリを使う
前回の線形モデルと類似のコードにしたい

演習用のファイル

データ：【気象庁共同プロジェクト】気象データのビジネス活用の元データのダウンロードからダウンロード。東京都時系列スポーツ飲料データタブのみ利用。
コード：quantile_nonlinear_regression.ipynb

1. 指数関数と二次関数による回帰の考え方

非線形モデルといっても推定式は次の２種類に限定します。

二次関数： $y = a + b_1x + b_2 x^2$
指数関数： $y=ae^{bx}$

二次関数
二次関数$y=a+b_1x + b_2x^2$による回帰は、説明変数 ($x$) について、事前に説明変数の２乗データ ($x^2$) を作成する工夫で対応します。２乗データを２つ目の説明変数$x_2$とみなせば、$$
y = a + bx_1 + c x_2
$$という線形モデルとして考えることができるからです。

指数関数
指数関数$y=ae^{bx}$による回帰は、対数を使って線形化することで簡単に実現できます。両辺対数を使って$$\log y = \log a + bx$$と変形、目的変数が$\log y$、切片は$\log a$、説明変数の項は$bx$となります。$a$や$b$の推定、$y=ae^{bx}$の形に戻すことで指数関数による回帰となります。

2. OLSと分位点回帰

最小二乗回帰（OLS） は、誤差の二乗和を最小化することで、説明変数に対する目的変数の「条件付き平均」を予測するモデルです。

分位点回帰は、誤差の絶対値を分位点に応じて重み付けして最小化することで、目的変数の中央値（50%点）や下位10%点、上位90%点などの「条件付き分位点」を予測するモデルです。たとえば、中央値（50%点）の分位点回帰は「条件付き中央値回帰」と呼ばれ、平均を利用したOLSよりも外れ値の影響を受けにくいという特徴があります。詳しい解説は、次の3つを参考にしてください。

OLSは「平均的にはこのくらい」という中庸な予測であるのに対して、分位点回帰は任意の分位点を選ぶことで、下振れリスク（悲観的シナリオ）や上振れチャンス（楽観的シナリオ）を明示的にモデル化できるのも特徴です。

3. データの準備

データの準備は簡単です。ダウンロードしてCSVファイルとして保存すればOKです。エクセル形式で読み込むこともできるのですが、なんとなくCSVファイルのほうがいいかと思いまして...

手順

【気象庁共同プロジェクト】気象データのビジネス活用の「元データのダウンロード」からダウンロードします。ファイル名はDL4.xls
「東京都時系列スポーツ飲料データ」タブを選択してCSVとして保存
　ファイル名はsports_temp.csv

3.1 ２乗データの追加

２次関数での予測をするために、平均気温を２乗したデータをsports_temp.csvのデータに追加します。

２乗データの追加

import pandas as pd

df = pd.read_csv("./data/sports_temp.csv")
df["平均気温2"] = df["平均気温"]**2

安直な列名ですが平均気温2に平均気温の２乗の項目が追加されています。

利用するデータである平均気温、平均気温2、販売指数の３種類について訓練データとテストデータに分割します。

データの分割

from sklearn.model_selection import train_test_split

x = df[["平均気温", "平均気温2"]]
t = df["販売指数"]
x_train, x_test, t_train, t_test = train_test_split(x,t, random_state=55)
print(x_train.head())

目的変数にt_train、説明変数にx_trainを利用して推定することになります。

4. 二次関数モデルでの分位点回帰

二次関数で回帰分析すると言っても、平均気温と２乗データの平均気温2の線形回帰
$$
販売指数 = a + b_1~平均気温 + b_2~平均気温2
$$
とみなすことができます。

分位点を0.1、0.5、0.9に設定した分位点回帰とOLSモデルで推定してみます。

二次関数モデル

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import japanize_matplotlib

# 1. 分位点の設定
taus = [0.1, 0.5, 0.9]

# 2. 説明変数と目的変数を設定
X = sm.add_constant(x_train)
y = t_train

# 3. 予測曲線を滑らかに描くために、気温の範囲を細かく設定
temp_range = np.linspace(df["平均気温"].min(), df["平均気温"].max(), 100)
predict_df = pd.DataFrame({"平均気温": temp_range, "平均気温2": temp_range ** 2}) # ２乗データも使うのでpredict_dfに２乗データも追加
predict_df = sm.add_constant(predict_df)


# 4. OLSでの二次関数モデル
ols_model = sm.OLS(endog=y, exog=X)
ols_result = ols_model.fit()
ols_a = ols_result.params.const
ols_b = ols_result.params.平均気温
ols_c = ols_result.params.平均気温2
ols_label = f"OLS: {ols_a:.2f}{ols_b:.3f}X+{ols_c:.4f}$X^2$"


# 5. 分位点回帰での二次関数モデル
model = sm.QuantReg(endog=y, exog=X)



# 6. グラフ描画のための設定
fig, ax = plt.subplots(figsize=(10,5))

# 6.1 テストデータの散布図
ax.scatter(x_test["平均気温"], t_test, color="skyblue", label="テストデータ", alpha=0.5)

# 6.2 OLS回帰のプロット
# 平均気温が一定間隔で並んでいるpredict_dfを使ってグラフを描画
ols_predicted_sales = ols_result.predict(predict_df)
ax.plot(temp_range, ols_predicted_sales, label=ols_label, linestyle="dotted")

# 6.3 分位点回帰のプロット
for t in taus:
    result = model.fit(q=t)
    a = result.params.const
    b1 = result.params.平均気温
    b2 = result.params.平均気温2
    sign1 = "+" if b1 >= 0 else "-"
    sign2 = "+" if b2 >= 0 else "-"
    label = f"{t}: {a:.2f}{sign1}{abs(b1):.3f}X{sign2}{abs(b2):.4f}$X^2$"

    # モデルを使って予測値を計算
    predicted_sales = result.predict(predict_df)
    ax.plot(temp_range, predicted_sales, label=label)

# グラフのタイトルとラベルを設定
ax.set_title("OLS・分位点回帰（二次関数）の比較")
ax.set_xlabel("平均気温")
ax.set_ylabel("販売指数")
ax.legend()
plt.show()

コードのポイント

3番：np.linspace(df["平均気温"].min(), df["平均気温"].max(), 100)によって気温の最小値から最大値を100分割したものを準備しておきます。
predict_dfも平均気温の２乗を追加してx_trainと同じ構造に合わせておきます。
6番：テストデータでもうまく推定できているかを確認したいので、今回はテストデータのみ表示させています。
6.3番：回帰式3本を描画するループです。label表示に数式を入れたので若干込み入って見えます。基本は、次の3つです。
1. result=model.fit(q=t)
2. result.predict(predict_df)を使った予測値の計算
3. ax.plot()による予測値の描画

テストデータの散布図、OLSの予測線、分位点３種類の予測線を描画したグラフが下図になります。直線よりも格好良く見えるのが曲線マジック!!

モデルでの予測図は上のようになります。水色の丸い点がテストデータの値、３本が実践が推定した式をグラフ化したものです。上から順番に、分位点が0.9、0.5、0.1と並んでいます。

0.5分位点での回帰と点線のOLSの回帰がかなり似ています。前回の線形モデル以上に類似しています

分位点 = 0.1（10％）
条件付き分布の下位10％を説明する直線なので、「ある平均気温のとき販売指数（売上）が低いほうに入るとしたら、このくらい」という悲観的シナリオに近い解釈ができます。
分位点 = 0.5（50%）
中央値での回帰なので、中央値と平均値が近い値のときは、OLSの線形回帰と似ています。「真ん中はこのくらい」という中庸な予測と解釈できます。
分位点 = 0.9（90％）
上位10％を説明する直線なので、「ある平均気温のとき販売指数（売上）が高いほうに入るとしたら、このくらい」という楽観的シナリオに近い解釈ができます。

5. 指数関数モデルでの分位点回帰

指数関数$y=ae^{bx}$の形で分位点回帰をしてみます。対数を利用して
$$
\log y = \log a + bx
$$
の形に変形することで線形モデルと同様に扱うことができそうです。目的変数である販売指数(y)をnp.log(y)にすることを忘れずに、回帰分析するだけです。

指数関数モデル

# 1. 分位点の設定
taus = [0.1, 0.5, 0.9]

#　2. 説明変数と目的変数を設定
X = sm.add_constant(x_train["平均気温"])
y = t_train
log_y = np.log(y)   # 目的変数は log をとるぞ〜

# 3. 予測曲線を滑らかに描くために、気温の範囲を細かく設定
temp_range = np.linspace(df["平均気温"].min(), df["平均気温"].max(), 100)
predict_df = pd.DataFrame({"平均気温": temp_range})
predict_df = sm.add_constant(predict_df)

# 4. OLS 指数関数の回帰
ols_model = sm.OLS(log_y, X)
ols_result = ols_model.fit()
ols_a = np.exp(ols_result.params.const)    # 元の関数のaに戻す
ols_b = ols_result.params.平均気温           # 元の関数のb
predicted_sales = ols_result.predict(predict_df)
y_pred_ols = np.exp(predicted_sales)
ols_label = f"OLS: y={ols_a:.2f}exp({ols_b:.3f}x)"

# 5. 分位点回帰での計算
qr_model = sm.QuantReg(log_y, X)


# 6. グラフ描画のための設定
fig, ax = plt.subplots(figsize=(10,5))
# 6.1 テストデータの散布図
ax.scatter(x_test["平均気温"], t_test, color="skyblue", label="テストデータ", alpha=0.5)

# 6.2 OLS回帰のプロット
ax.plot(temp_range, y_pred_ols, label=ols_label, linestyle="dotted")


# 6.3 グラフ表示
for t in taus:
    qr_result = qr_model.fit(q=t)      # t-分位点回帰
    predicted_sales = qr_result.predict(predict_df)
    y_pred_qr = np.exp(predicted_sales) # 予測値を元に戻す
    a = np.exp(qr_result.params.const)  # 元の関数のa
    b = qr_result.params.平均気温
    qr_label = f"{t}: y={a:.2f}exp({b:.3f}x)"
    ax.plot(temp_range, y_pred_qr, label=qr_label)

# グラフのタイトルとラベルを設定
ax.set_title("OLS・分位点回帰（指数関数）の比較")
ax.set_xlabel("平均気温")
ax.set_ylabel("販売指数")
ax.legend()
plt.show()

コードのポイント

2番：目的変数である販売指数をnp.log(y)とします。
4番：推定した切片の値は、log aだったので、最初のaの値はexp(log a)とすればOK。予測値もlog yなので、exp(predicted_saled)でyの値に戻します。
6.3番：4番と同様、切片と予測値の値をexp( )して戻します。

指数関数を利用した分位点回帰のグラフが次のものです。