LoginSignup
1
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@AzukiImo

【分位点回帰】楽観的予測〜悲観的予測

Posted at

概要

飲料水.jpg

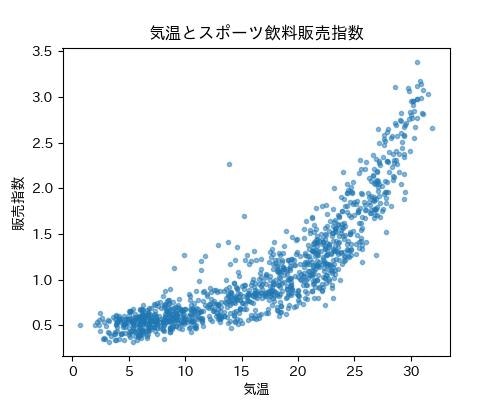
「暑い日には飲料水がよく売れる！」経験的に理解している現象だと感じます。この関係性を統計的に分析しているのが全国清涼飲料連合会のプロジェクトです。

sales_temp.jpg

全国清涼飲料連合会が気象庁との共同プロジェクトで公開している気象データのビジネス活用では、このような気温と飲料販売の関係について、実際のデータを用いた統計分析の結果を見ることができます。スポーツ飲料、炭酸飲料、果汁飲料の販売データと気象データを組み合わせたこの分析は、統計学やデータサイエンスの実践例として非常に興味深い内容となっています。また、データやグラフなどもダウンロードできる仕様で、再現実験もでき、非常に勉強になります。個人的にもとても参考になりました:heart_eyes::heart_eyes::heart_eyes:

今回は、このプロジェクトで公開されている東京都のデータを活用し、気温とスポーツ飲料販売指数の関係を「分位点回帰」という手法で分析します。通常の線形回帰では平均的な関係性しか捉えられませんが、分位点回帰を用いることで、気温の影響が販売量の分布全体にどのように及ぶのかを詳細に把握することが可能になります。

演習用のファイル

1. OLSと分位点回帰

最小二乗回帰（OLS） は、誤差の二乗和を最小化することで、説明変数に対する目的変数の「条件付き平均」を予測するモデルです。

分位点回帰は、誤差の絶対値を分位点に応じて重み付けして最小化することで、目的変数の中央値（50%点）や下位10%点、上位90%点などの「条件付き分位点」を予測するモデルです。たとえば、中央値（50%点）の分位点回帰は「条件付き中央値回帰」と呼ばれ、平均を利用したOLSよりも外れ値の影響を受けにくいという特徴があります。

OLSは「通常、平均的にはこのくらい」という中庸な予測であるのに対して、分位点回帰は任意の分位点を選ぶことで、下振れリスク（悲観的シナリオ）や上振れチャンス（楽観的シナリオ）を明示的にモデル化できるのも特徴です。

詳しい解説は、次の３つを参考にしてください。理論的な解説やPythonでの実装方法が解説されています。

2. データの準備

データの準備は簡単です。ダウンロードしてCSVファイルとして保存すればOKです。エクセル形式で読み込むこともできるのですが、なんとなくCSVファイルのほうがいいかと思いまして:sweat:...

手順

  1. 【気象庁共同プロジェクト】気象データのビジネス活用の「元データのダウンロード」からダウンロードします。ファイル名はDL4.xlsとなっています。
  2. 「東京都時系列スポーツ飲料データ」タブを選択してCSVとして保存すれば終了です。
  3. 　CSVファイルは、dataフォルダにsports_temp.csvとして保存しました。

このあとは、

  • pandasで読み込む
  • statsmodels.apiで回帰分析
  • matplotlibでグラフ作成

という定番の流れになります。

3. 線形モデル

statsmodels.apiのコマンド使えば、分位点回帰といっても通常の回帰分析と同じです。QuantReg(y,X) を利用するだけです。

3.1 使い方の基本

statsmodels.apiを利用した分位点回帰はQuantReg(y,X) を利用するだけです。すべてのデータを利用したサンプルコードで使い方の流れの確認してみます。

基本コード「分位点回帰 (q=0.5)」
# 1. CSVファイルの読み込み
import pandas as pd
df = pd.read_csv("./data/sports_temp.csv") # データフレームの販売指数・平均気温を使います

# 2. 主要な部分　分位点回帰の基本コード
# ライブラリ
import statsmodels.api as sm

# 説明変数(X)と目的変数(y)を設定
X = sm.add_constant(df["平均気温"])  # add_constantで切片付き
y = df["販売指数"]

# 分位点回帰の実行 (qに分位点を中央値に指定する場合 q=0.5)
model = sm.QuantReg(endog=y, exog=X)
result = model.fit(q=0.5)

# 結果の表示
print(result.summary())
print(f"切片：{result.params.const:.3f}")
print(f"平均気温係数：{result.params.平均気温:.3f}")

QuantReg(y,X) でモデルを決めて、model.fit() で推定するという流れになります。結果の表示には、定番パターンの summary() が使えます。係数や切片の個別の取得も可能です。

summaryの表示(分位点：0.5)
                         QuantReg Regression Results                          
==============================================================================
Dep. Variable:                販売指数   Pseudo R-squared:               0.5008
Model:                       QuantReg   Bandwidth:                      0.1176
Method:                 Least Squares   Sparsity:                       0.6160
Date:                Sun, 24 Aug 2025   No. Observations:                 1126
Time:                        09:04:06   Df Residuals:                     1124
                                        Df Model:                            1
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const        　0.0890      0.022      4.122      0.000       0.047       0.131
平均気温       　0.0574      0.001     48.290      0.000       0.055       0.060
==============================================================================
切片：0.089
平均気温係数：0.057

決定係数に相当する疑似決定係数があるのですが、曲線ぽい傾向を線形で回帰しているので0.5と案外低い:sweat_smile:
縦軸が販売指数で数値が小さいことから平均気温の係数の値も小さく見えますが、係数は問題なさそうです。

次からがいよいよ主要な内容となります。

3.2 ３種類の分位点で可視化

販売指数と平均気温の散布図をから、同じ気温でも販売指数にかなり上下に幅があります1。上位（90%）、中央値（50%）、下位（10%）、の３種類の分位点を利用しました。解釈はだいたい次のようになります。

  1. 分位点 = 0.1（10％）
    条件付き分布の下位10％を説明する直線なので、「ある平均気温のとき販売指数（売上）が低いほうに入るとしたら、このくらい」という悲観的シナリオに近い解釈ができます。

  2. 分位点 = 0.5（50%）
    中央値での回帰なので、中央値と平均値が近い値のときは、OLSの線形回帰と似ています。「真ん中はこのくらい」という中庸な予測と解釈できます。

  3. 分位点 = 0.9（90％）
    上位10％を説明する直線なので、「ある平均気温のとき販売指数（売上）が高いほうに入るとしたら、このくらい」という楽観的シナリオに近い解釈ができます。

CSVファイルを読み込むことから始めます。データを、推定に利用する訓練データと検証に利用するテストデータとに分割します。

データの読み込みと分割
# 1. ライブラリの読み込み
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.model_selection import train_test_split

# 2. pandasでCSVファイルを読み込む
df = pd.read_csv("./data/sports_temp.csv")

# 3. train_test_splitで分割
x = df["平均気温"]
t = df["販売指数"]
x_train, x_test, t_train, t_test = train_test_split(x,t, random_state=55)

pandasでCSVファイルを読み込んで、train_test_splitで推定につかう訓練用データと検証用のテストデータとに分割します。

x_trainとt_trainが推定に利用されるデータになります。x_trainを説明変数に、t_trainを目的変数（教師データ）として QuantReg(目的変数, 説明変数) を使います。

分位点回帰
# 1. 分位点の設定
taus = [0.1, 0.5, 0.9]

# 2. 説明変数と目的変数を設定　訓練用データで推定
# x_train, t_trainをつかう
X = sm.add_constant(x_train)
y = t_train

# 3. 予測曲線を滑らかに描くために、気温の範囲を細かく設定
temp_range = np.linspace(df["平均気温"].min(), df["平均気温"].max(), 100)
predict_df = pd.DataFrame({"平均気温": temp_range})
predict_df = sm.add_constant(predict_df)


# 4. 分位点回帰モデル作成
model = sm.QuantReg(endog=y, exog=X)


# 5. グラフ描画のための設定
fig, ax = plt.subplots(figsize=(10,5))

# 6. 全データとテストデータの散布図
# ax.scatter(df["平均気温"], df["販売指数"], color="skyblue", label="全データ", alpha=0.6)
ax.scatter(x_test, t_test, color="skyblue", label="テストデータ", alpha=0.5)

# 7. 分位点のごとのグラフを重ねて描画
for t in taus:
    result = model.fit(q=t)           # 分位点がtのときの推定結果
    a = result.params.const           # 定数項 a
    b = result.params.平均気温         # 係数 b
    label = f"{t}: {a:.3f}+{b:.3f}X"  # y=a+bx
    
    # モデルの推定値を使って予測値を計算、グラフを描画
    predicted_sales = result.predict(predict_df)         # predict_dfは綺麗に並んだ温度
    ax.plot(temp_range, predicted_sales, label=label)    # 予測曲線をプロット

ax.set_title("テストデータと分位点回帰")
ax.set_xlabel("平均気温")
ax.set_ylabel("販売指数")
ax.legend()
plt.show()

コードのポイント

  • 3番：回帰分析によって、切片 ($a$) と係数 ($b$) の2つが求まります。$y=a+bx$をグラフに描画する時、$x$の値が一定間隔で並んでいると綺麗な直線が描画されます。np.linspace(df["平均気温"].min(), df["平均気温"].max(), 100)によって気温の最小値から最大値を100分割したものを準備しておきます。predict_dfもx_trainと同じような構造に合わせておきます。

  • 6番：テストデータでもうまく推定できているかを確認したいので、今回はテストデータのみ表示させています。

  • 7番：回帰直線3本を描画するループです。label表示に回帰式を入れたいので若干込み入って見えます。基本は、次の3つです。

    1. result=model.fit(q=t)
    2. result.predict(predict_df)を使った予測値の計算
    3. ax.plot()による予測値の描画

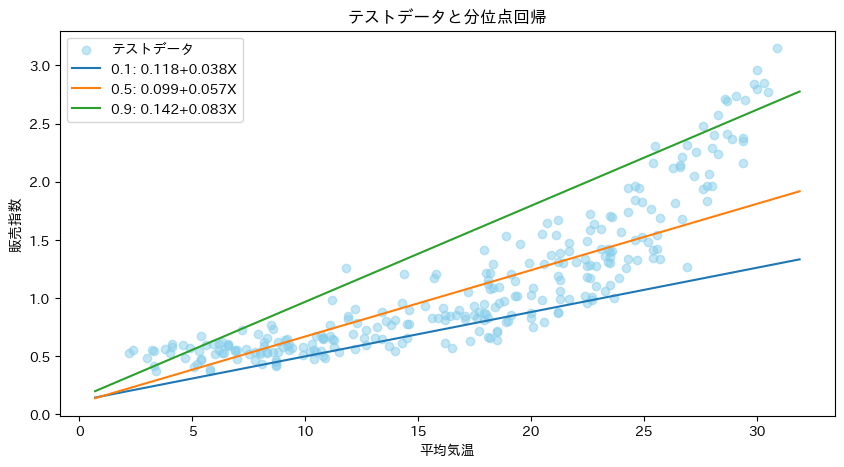
線形モデルでの予測図は次のようになります。水色の丸い点がテストデータの値となります。直線３本が推定した式をグラフ化したものです。上から順番に、分位点が0.9、0.5、0.1と並んでいます。

image.png

緑色の直線が上位10%で、青い直線が下位10%となります。この間に挟まれるのが80%ということになります。オレンジ色の直線が中央値に相当します。ほぼ0.1〜0.9の直線の幅に含まれています。

ちなみに、気温が高いと販売指数のばらつきも大きいみたいですね〜。

使い方＆解釈１

  • 売上好調の場合：分位点0.9のパターンで予測
  • 売上低調の場合：分位点0.1のパターンで予測

使い方＆解釈２

  • 楽観的な予測：分位点0.9の回帰直線で、うまくすればこの販売指数レベルになるはず！
  • 悲観的な予測：分位点0.1の回帰直線で、最低このレベルはクリアできるはず！

3.3 OLSの線形回帰モデルと比較

中央値での回帰モデルが分位点0.5の線形回帰モデルになります。中央値と平均値が近い場合、分位点0.5の回帰直線とOLSの回帰直線が似てくるはず！ということで、平均的な動きの代表としてOLSによる線形モデルも先程のグラフに追加してみました。

OLSの線形回帰を追加
# 1. 分位点の設定
taus = [0.1, 0.5, 0.9]

# 2. 説明変数と目的変数を設定　訓練用データで推定
# x_train, t_trainをつかう
X = sm.add_constant(x_train)
y = t_train

# 3. 予測曲線を滑らかに描くために、気温の範囲を細かく設定
temp_range = np.linspace(df["平均気温"].min(), df["平均気温"].max(), 100)
predict_df = pd.DataFrame({"平均気温": temp_range})
predict_df = sm.add_constant(predict_df)

# 4. OLS線形回帰
ols_model = sm.OLS(endog=y, exog=X)
ols_result = ols_model.fit()
ols_a = ols_result.params.const
ols_b = ols_result.params.平均気温
ols_label = f"OLS: {ols_a:.3f}+{ols_b:.3f}X"



# 5. 分位点回帰モデル
model = sm.QuantReg(endog=y, exog=X)

# 6. グラフ描画のための設定
fig, ax = plt.subplots(figsize=(10,5))

# 7. テストデータの散布図
ax.scatter(x_test, t_test, color="skyblue", label="テストデータ", alpha=0.5)

# 8. OLS線形回帰のプロット
# 平均気温が一定間隔で並んでいるpredict_dfを使って直線を描画
ols_predicted_sales = ols_result.predict(predict_df)
ax.plot(temp_range, ols_predicted_sales, label=ols_label, linestyle="dotted")

# 9. 分位点ごとのグラフを重ねて描画
for t in taus:
result = model.fit(q=t)           # 分位点がtのときの推定結果
    a = result.params.const           # 定数項 a
    b = result.params.平均気温        # 係数 b
    label = f"{t}: {a:.3f}+{b:.3f}X"  # y=a+bx
    
    # モデルの推定値を使って予測値を計算、グラフを描画
    predicted_sales = result.predict(predict_df)
    ax.plot(temp_range, predicted_sales, label=label)    # 予測曲線をプロット

ax.set_title("OLSと分位点回帰比較")
ax.set_xlabel("平均気温")
ax.set_ylabel("販売指数")
ax.legend()
plt.show()

コードのポイント
OLSの推定と予測値の計算やグラフ描画以外は先程と同じです。

  • 4番：OLSによる線形回帰です。sm.OLS() を利用して推定します。label表示のために、込み入って見えますが、基本はOLS() と fit() だけです。OLS線形回帰の決定係数は0.74でした。
  • 8番：ols_result.predictでOLSの結果を予測値を計算、ax.plot でグラフにします。

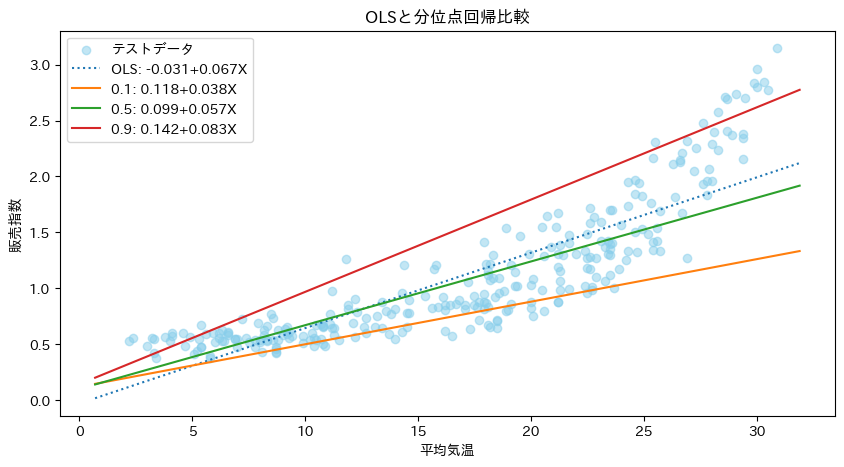
点線がOLSの線形回帰モデルとなります。分位点0.5の中央値を利用した回帰とOLSの回帰、数値はやや異なりますが、グラフはかなり似ています。正確には異なる回帰式の係数を比較検定するべきかな:sweat:

image.png

解釈

  • 楽観的（分位点0.9）： 気温が1度上昇すると販売指数は、0.083ポイント上昇
  • 悲観的（分位点0.1）： 気温が1度上昇すると販売指数は、0.038ポイント上昇
  • 平均的予測（OLS回帰）： 気温が1度上昇すると販売指数は、0.067ポイント上昇
  • 中庸（分位点0.5）： 気温が1度上昇すると販売指数は、0.057ポイント上昇
解釈 分位点/OLS 気温＋１度の効果
楽観的 0.9 0.083 上昇
中庸 0.5 0.057 上昇
悲観的 0.1 0.038 上昇
平均的 OLS 0.067 上昇

分位点回帰は、1978年頃（もしかしたら更に昔からあるかもしれない）まで遡れるようです。幅を持って予測できるのは区間推定っぽくて面白いかも:cactus:

参考

  • Emerging Trends in the Social and Behavioral Sciencesに収録されている
    Fitzenberger, Wilke (2015) "Quantile Regression Methods",
    が手短にまとまっている解説書です。20ページくらいだったかな。

  • 教科書だと、
    Roger Koenker (2005) Quantile Regression (Econometric Society Monographs Book 38)
    が有名です。PDF版？が公開されていますが150ページもあるので大変です。

  • 分位点回帰を提案した論文。アイディアはかなり古いみたいです。
    Koenker, Roger and Gilbert Bassett. (1978) “Regression Quantiles.” Econometrica. January, 46:1, pp. 33–50.

注

  1. 平均気温以外の他の要因を追加することで販売指数をもう少し上手に説明できる可能性があります。時間があるときにでも試してみたい:cactus: ↩

1
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?