🔰PyTorchでニューラルネットワーク基礎 #16 【時系列・因果畳み込み】

概要

個人的な備忘録を兼ねたPyTorchの基本的な解説とまとめです。

第15回で因果畳み込みについて簡単にまとめてみました。新しいネットワーク層なら使ってみたい!!!! ということで、今回は港区のごみ収集量のデータを利用して、月ごとの可燃ごみ収集量を予測する演習を通して因果畳み込みを使ってみたいと思います。

図：テストデータで確認した結果

２月は日数が少ないのが影響しているのかな？ちゃんと特徴を捉えているように感じます。

方針

1. できるだけ同じコード進行
2. できるだけ簡潔（細かい内容は割愛）
3. 特徴量などの部分，あえて数値で記入（どのように変わるかがわかりやすい）

演習用のファイル

• データ minatoku_gomi.csv
• コード sample_16.ipynb

1. 因果畳み込みを利用した時系列分析

データについて

港区オープンデータカタログサイトのごみ収集量データを利用します。

• 港区のごみ収集量【速報値】
• 2013年〜2022年：月次データ

年度ごとにデータがまとめられています。gitにはすでに種類、収集量、月データのみ抽出した形の加工したcsvファイルをおいてあります。

出典と加工

• 出典：港区オープンデータカタログサイト¹
• 港区のごみ収集量【速報値】
• 2025年8月1日に確認
• 港区のごみ収集量データからごみの種類（可燃ごみ、不燃ごみ、粗大ごみ、管路収集）と月データに抽出加工して作成

因果畳み込みを利用して可燃ごみの収集量を予測するニューラルネットワークを構築していきます。新しく追加される事項は、ネットワーク層の独自クラスを作成する部分となります。

追加項目

• クラスを利用してCausalConv1dのネットワーク層を作成

2. コードと解説

PyTorchによるプログラムの流れを確認します。基本的に下記の５つの流れとなります。Juypyter Labなどで実際に入力しながら進めるのがオススメ

• データの読み込みとtorchテンソルへの変換　(2.1)
• ネットワークモデルの定義と作成　(2.2)
• 誤差関数と誤差最小化の手法の選択　(2.3)
• 変数更新のループ　(2.4)
• 検証　(2.5)

2.1 データの読み込み

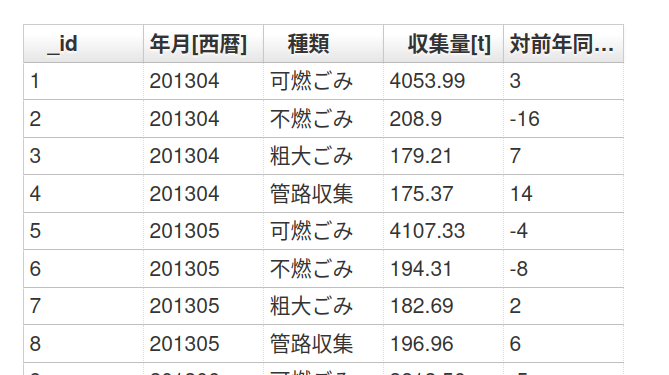
pandasで年月をインデックスに指定してminatoku_gomi.csvを読み込むと、図表のような形になります。可燃ごみの収集量と月を入力データとして、翌月の可燃ごみ収集量を教師データとする形でデータを作成します。データ作成部分を不燃ごみや粗大ごみに変更することももちろん可能です。粗大ごみは月ごとの特徴が面白いかも

1. 「種類」列の「可燃ごみ」で絞り込む
2. 「収集量」と「月」を抽出

窓サイズ３で入力データを作成していきます。窓サイズに根拠はありません。適宜数値を変更すると面白いと思います。ただ、データ数が少ないので長い窓サイズを指定するのが難しいかな

データの読み込み

import pandas as pd
import numpy as np
import torch
import torch.nn as nn

data = pd.read_csv("data/minatoku_gomi.csv",index_col="年月")

scaling_factor = 1_000
kanen = data[data["種類"]=="可燃ごみ"]["収集量"]/scaling_factor
month = data[data["種類"]=="可燃ごみ"]["月"]
kanen_list = kanen.to_list()
month_list = month.to_list()

win_size = 3  # 入力データの窓サイズ
x0 = [kanen_list[i:i+win_size] for i in range(len(kanen_list)-win_size)]
x1 = [month_list[i:i+win_size] for i in range(len(month_list)-win_size)]
x0 = np.array(x0)
x1 = np.array(x1)

t = kanen_list[win_size:]

コードのポイント

• 可燃ごみの収集量を1000で割り算して値を一定の範囲にまとめておきます。単位が「メガトン」になっている状況です
• 可燃ごみの収集量をkanen_list、月はmonth_listとしてリストに変換後、窓サイズ３でそれぞれデータを作成します
• 可燃ごみの窓サイズ３データをx0、月の窓サイズ３データをx1とします
• 教師データは翌月の可燃ごみ収集量となります

テンソルへ変換

device = "cuda" if torch.cuda.is_available() else "cpu"
print(f"device: {device}")


x0 = torch.FloatTensor(x0).reshape(x0.shape[0], 1, x0.shape[1]).to(device)
x1 = torch.FloatTensor(x1).reshape(x1.shape[0], 1, x1.shape[1]).to(device)
x  = torch.cat([x0,x1], dim=1)
t = torch.FloatTensor(t).view(-1,1).to(device)


period = 20
x_train = x[:-period]
x_test = x[-period:]
t_train = t[:-period]
t_test = t[-period:]

# x_train.shape: (96, 2, 3)
# x_test.shape:  (20, 2, 3)
# t_train.shape: (96, 1)
# t_test.shape:  (20, 1)

コードのポイント

• x0とx1を結合して、「可燃ごみ収集量」と「月」の２チャンネルのデータにします
• 入力データの形状は、（バッチサイズ、チャンネル数=２，系列長=３）
• 後半の20期間をテストデータとします。総データ数が少ないのでテストデータを12ヶ月（１年分）にしても良いかもしれません

2.2 ネットワークモデルの定義

因果畳み込みによって時系列データから特徴量を抽出し、線形層で回帰モデルに仕上げます。ネットワーク構造は特徴量を捉えるcausal_layersと回帰分析に仕上げるregressorから構成されます。PyTorchには因果畳み込みそのものを表すネットワーク層は現状（2025年8月時点では）存在しません。Conv1dを利用してCausalConv1dクラスを作成します。

自作のネットワーク層を作成すると言っても、基本は今までのネットワーク構造を作成するコードとなんら変わりありません。

CausalConv1dクラスに次の２点を指定することになります。

1. __init__()　に nn.Conv1d( ) を記述
2. forward( ) の部分でnn.Conv1dの出力値の右側を削除する

下記のコードでは、self.kernel_size = kernel_sizeや self.dilation = dilationを使って、因果畳み込みで利用するpaddingのサイズを自動で決めています

CausalConv1dクラス

class CausalConv1d(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, dilation=1):
        super().__init__()
        self.kernel_size = kernel_size
        self.dilation = dilation
        self.padding = (kernel_size - 1) * dilation
        self.conv = nn.Conv1d(in_channels, out_channels, kernel_size, padding=self.padding, dilation=self.dilation)

    def forward(self, x):
        h = self.conv(x)
        return h[:, :, :-self.padding]

コードのポイント

• nn.Conv1dの引数をそのまま使えるように、CausalConv1dの引数にも同じものを指定しておきます
• __init__() にnn.Conv1dの定義を記述
• forward( ) にnn.Conv1dの出力値の右側を削除する

実際に学習するネットワーク構造を記述します。作成したCausalConv1dを、これまでのnn.Linearやnn.Conv2dのように利用するだけです。

ネットワーク構造

class DNN(nn.Module):
    def __init__(self):
        super().__init__()
        # 特徴量の抽出       
        self.causal_layers = nn.Sequential(
            CausalConv1d(in_channels=2, out_channels=10, kernel_size=3),
            nn.ReLU(),
            CausalConv1d(in_channels=10, out_channels=10, kernel_size=3),
            nn.ReLU(),
            CausalConv1d(in_channels=10, out_channels=10, kernel_size=3)
        )
        # 回帰分析のレイヤー　10チャンネルｘ３（データの系列長）
        self.regressor = nn.Sequential(
            nn.Flatten(),
            nn.Linear(in_features=10*3, out_features=1)
        )
        
    def forward(self, x):
        h = self.causal_layers(x)
        y = self.regressor(h)
        return y

model = DNN()
model.to(device)

コードのポイント

• nn.Sequential()を利用して、特徴量の抽出ブロック(causal_layers)と回帰モデルにあてはめるブロック(regressor)とに分けて記述します²
• causal_layersには因果畳み込みを３層配置
• regressorはnn.Linearで最終出力を１に設定します

torchinfoライブラリでネットワーク構造を確認してみました。summary()の入力データの形状に関する引数は、（バッチサイズ=１，チャンネル数=2、系列長=3)となります。

ネットワーク構造

from torchinfo import summary
summary(model, (1,2,3))

==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
DNN                                      [1, 1]                    --
├─Sequential: 1-1                        [1, 10, 3]                --
│    └─CausalConv1d: 2-1                 [1, 10, 3]                --
│    │    └─Conv1d: 3-1                  [1, 10, 5]                70
│    └─ReLU: 2-2                         [1, 10, 3]                --
│    └─CausalConv1d: 2-3                 [1, 10, 3]                --
│    │    └─Conv1d: 3-2                  [1, 10, 5]                310
│    └─ReLU: 2-4                         [1, 10, 3]                --
│    └─CausalConv1d: 2-5                 [1, 10, 3]                --
│    │    └─Conv1d: 3-3                  [1, 10, 5]                310
├─Sequential: 1-2                        [1, 1]                    --
│    └─Flatten: 2-6                      [1, 30]                   --
│    └─Linear: 2-7                       [1, 1]                    31
==========================================================================================
Total params: 721
Trainable params: 721
Non-trainable params: 0
Total mult-adds (Units.MEGABYTES): 0.00
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.00
Estimated Total Size (MB): 0.00
==========================================================================================

これ以降の手順は、初回から変わらずです

2.3 誤差関数と誤差最小化の手法の選択

回帰モデルなので、誤差関数に平均二乗誤差を指定します。

誤差関数

criterion = nn.MSELoss() 
optimizer = torch.optim.AdamW(model.parameters())

2.4 変数更新のループ

学習用に作成したx_trainと教師データt_trainを使って変数をアップデートしていきます。

変数の更新

LOOP = 2000

model.train()
for epoch in range(LOOP):
    optimizer.zero_grad()
    y = model(x_train)
    loss = criterion(y,t_train)
    if (epoch+1)%200 == 0:
        print(epoch,"\tloss:", loss.item())
    loss.backward()
    optimizer.step()

# 199 	loss: 0.033827029168605804
# 399 	loss: 0.027542300522327423

LOOPの回数は適当ですので、損失の減少具合で適宜判断してください

2.5 検証

テスト用のデータx_testを利用して予測結果を検証します。

予測値の計算

model.eval()
with torch.inference_mode():
    pred = model(x_test)

# cpu()、numpy()に戻さないとmatplotlibで表示できないぞ〜
pred=pred.cpu().detach().numpy()
real = t_test.detach().cpu().numpy()

グラフ表示

ささやかながら、予測値にscaling_factorを掛け算してデータ加工前の単位である「トン」に戻しておきました。

可視化

import matplotlib.pyplot as plt
import japanize_matplotlib

s=x_train.shape[0]

plt.figure(figsize=(10,4))

plt.plot(kanen.index.values[win_size+s:], real*scaling_factor, label="可燃ごみ実測", marker=".")
plt.plot(kanen.index.values[win_size+s:], pred*scaling_factor,  label="予測値", marker="*")

plt.xticks(rotation=75, ha='right')
plt.title("可燃ごみ")
plt.xlabel("月")
plt.ylabel("収集量【t】")
plt.legend()
plt.show()

一期前を利用するナイーブ予測よりは断然良い結果なのですが まあ、まあというところでしょうか？５月、６月、10月、11月のズレが気になりますね。ごみ収集量なので実測値が予測値よりも小さいことは良いことのようにも感じますが......
やはり２月は可燃ごみの量が少ないんですね。日数が少ないと大きな違いになるんだな〜

基本的な指標でチェックしてみました³。毎回結果は変わりますが、ほぼこの数値前後だと思います。DM統計量はテストデータのサンプル数が少ないので参考程度です

指標		値
MAE	平均絶対誤差	0.0792
RMSE	平均平方二条誤差	0.0953
MAPE	平均絶対誤差率	2.0346%
R²	決定係数	0.7229
MASE	平均絶対スケール誤差	0.313 < 1
Direction Accuracy	平均方向精度	0.789 (78.9%)
DM統計量	ダイボールド・マリアーノ検定統計量（ナイーブと比較）	-2.472
p値		0.012 < 0.05

MAEが0.08です。1,000で割り算して計算していたので、1,000倍すれば、単位が「トン」になります。平均として80トンくらいのと誤差になります。MASE=0.3<1なので1期前のナイーブ予測よりもかなり良いことがわかりますが、ごみ収集量なので前年同月で予測するほうが当たるかな？

前年同月を加えてグラフを描画してみたのですが、う〜、どうかな？

指標でもチェックしてみた。

指標		因果畳み込みモデル	前年同月モデル
MAE	平均絶対誤差	0.0792	0.0996
RMSE	平均平方二条誤差	0.0953	0.1192
MAPE	平均絶対誤差率	2.0346%	2.5594%
R²	決定係数	0.7229	0.5670
MASE	平均絶対スケール誤差	0.313 < 1	0.862 <1
Direction Accuracy	平均方向精度	0.789 (78.9%)	0.632 (63.2%)

深層学習の面目を保ったか少しですが、因果畳み込みモデルのほうが良さそう⁴。「昨年は、○○だったな〜」という直感的な前年同月、なかなかいい予測値です。

ダイボールド・マリアーノ検定で因果畳み込みモデル（モデル１）と前年同月モデル（モデル２）を比較してみた。

	統計量	p値	有意差あるか
DM統計量	-1.207	0.121	No

サンプルデータが少ないので数値は参考程度ですが、２つのモデルに有意な差があるとは言えないっぽい。このあたりはグラフの見た目の感覚と一致していますね。

次回

いろいろ試したいことがあるので、どうなるのかわかりませんが、予測値に幅をもたせる方向か？因果畳み込みによる時系列分析の続きあたりかな

目次ページ

注

1. 各都道府県から市区町村（？）にいたるまで様々な公共データが公開されているようです。 ↩

2. nn.Sequentialを使ったネットワーク構造の記述については第13回を参考にしてください。torch.nn.Sequentialの使い方と実際のユースケースを解説も非常にわかりやすいです。 ↩

3. ここで登場している指標の解説は第9.5回を参考にしてください。 ↩

4. 2種類のモデルの指標の数値を見た目判定していますが、統計的な判定をすることもできるみたい。 ↩