概要
Transformer Encoderを利用した文章分類の注意行列や重みを可視化するための準備として、PyTorchでのMultiHeadAttentionの実装についてすこしだけ掘り下げてみます1。
Transformerの論文 (Attention is All You Need) での説明とPyTorchでのMultiheadAttentionの実装では、数学的には等価ですが、アプローチがやや異なります。論文では説明重視の方法で、PyTorchは実行速度を重視した構成になっているようです。PyTorchの実装にできるだけ即した形でマルチヘッドアテンションの動きを確認してみたいと思います。
これで、head毎のattention weightsを抽出できるようになるはず🔥
演習用のファイル
1. マルチヘッドアテンション
複数のヘッドで注意機構の計算を行う部分だけ確認してみます。
1.1. 論文(Attention is All You Need)流
論文では、MultiHeadAttentionの出力を次のように説明しています。
-
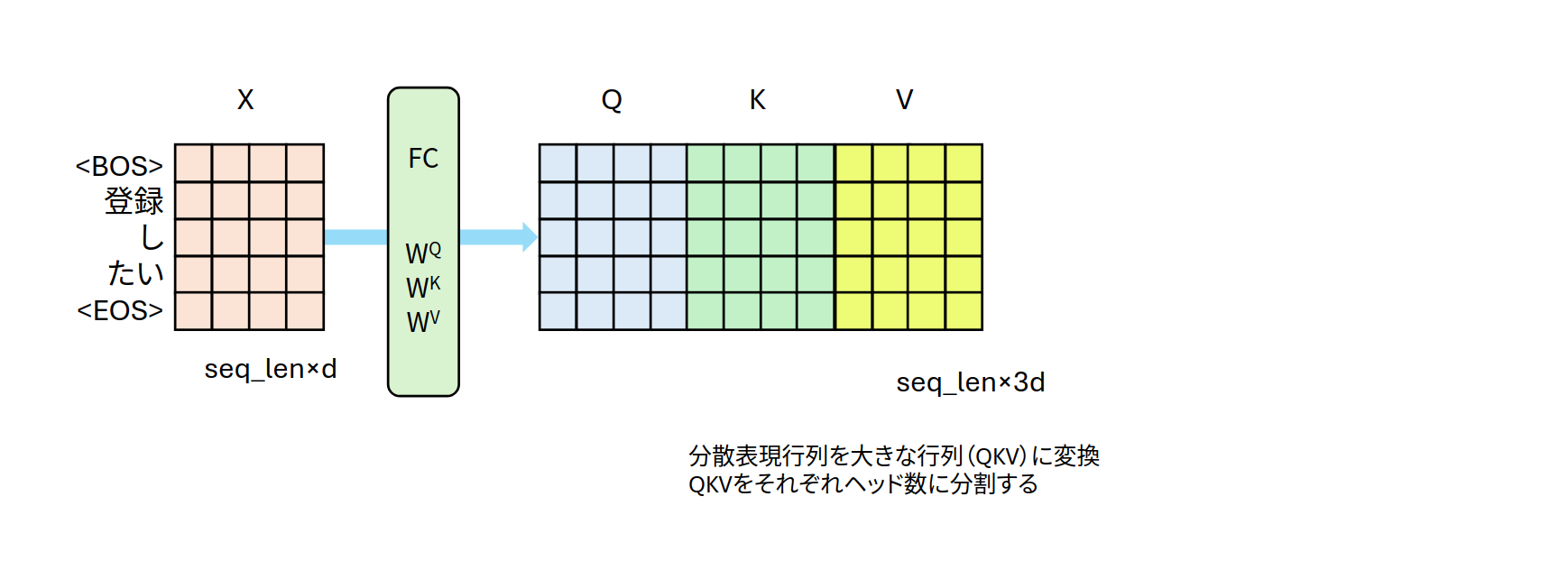
分散表現行列$X$に$W^Q, W^K, W^V$行列を掛けて クエリ、キー、バリュー行列$Q, K, V$ を計算する。
- $Q = XW^Q$
- $K = XW^K$
- $V = XW^V$
-
$Q, K, V$に $h$(ヘッドの数)個の行列$W_i^Q, W_i^K, W_i^V$を掛け算して、$Q_i, K_i, V_i$を用意する。
- $Q_i = QW_i^Q$
- $K_i = KW_i^K$
- $V_i = VW_i^V$
-
それぞれの$Q_i, K_i, V_i$でattentionの計算を行う。
head_i = \text{Attention}(Q_i, K_i, V_i) = \text{softmax}(\frac{Q_i K_i^T}{\sqrt{d}}) V_i -
ヘッドを集めて、$W^O$を掛け算し、$X$と同じ形状で出力する。
\text{MultiHead}(Q,K,V) = \text{Concat}(head_1,…,head_h) W^O
$Q, K, V$に各ヘッドごとに異なる行列を用いて$Q_i, K_i, V_i$ を作り、それぞれでattentionを計算 してから concat する形になっています1。
ここで、$d_{\text{model}}$ (分散表現の次元・埋め込み次元)を $h$ (ヘッド数)で割り算した値を$d$と表記しています。$d=d_{\text{model}}/h$はクエリベクトルやキーベクトルの次元となります2。
1.2. PyTorchでの計算手順
PyTorchでの実装についてすこしだけコードを覗いてみたいと思います。
PyTorch の実装では、
-
分散表現行列$X$に行列$W$ ($W^Q, W^K, W^V$を縦に結合したような行列)を掛けて $Q, K, V$ を計算
-
$Q, K, V$ の埋め込み次元 ($d_{\text{model}}$次元) をヘッド数 (h) で等分割して、ヘッド用の行列を作成
- $Q=[Q_1,...,Q_i,...,Q_h]$
- $K=[K_1,...,K_i,...,K_h]$
- $V=[V_1,...,V_i,...,V_h]$
-
分割されたで$Q_i, K_i, V_i$を利用して、ヘッドごとのattentionを計算
$$head_i = \text{Attention}(Qi, Ki, Vi)$$ -
各ヘッドの出力を concatして、$X$と同じ形状で出力
$$
\text{MultiHead}(Q,K,V) = \text{Concat}(head_1,…,head_h) W^O
$$
という流れになっています。
論文で解説されている方法は、ヘッド数の行列を準備して分散表現行列を小さく分け、順番にattention weightsを求めて、まとめ上げていく流れになります。一方、PyTorchでは、分散表現行列に大きな行列を掛け算して、$Q, K, V$を順番にスライスし、attention weightsを求めていく形になります。論文の「$X$から$Q=XW^Q$」、「$Q$から$Q_i=QW_i^Q$」へという流れを1回の掛け算で行っていることになります3。
ヘッド数での分割や注意行列・attention weightsなどをイラストとコードで確認したいと思います。ついでに、論文の説明文に即した計算方法とPyTorchのMultiHeadAttentionの出力が等しいことも数値でチェックしてみましょう![]()
ドキュメントとコード
- MultiheadAttentionのDocument: 使い方のドキュメント
- MultiheadAttentionのクラス:ソースコード
- 関連するソースコード functional.py: 6078行目付近に登場する関数 multi_head_attention_forward() の定義に流れの詳細が書かれています。行数ですが、ずれている可能性がありますよ〜
2. PyTorchでのMultiheadAttention
確認作業は、自己注意を前提として進めていきます![]()
2.1. nn.MultiheadAttentionでそのまま計算
準備
- 系列長:5 (seq_len)
- 分散表現の次元:4 (embed_dim)
- 分散表現行列:5×4行列 (X) 文章を行列化したもの
- query (Q), key (K), value (V)と表記
- ヘッド数:2 (num_heads)
5×4の行列Xを入力データとして、PyTorchのMultiheadAttention()を適用してみます。
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(55) # torch.randnをランダムにしたい場合は外す
seq_len = 5
embed_dim = 4
num_heads = 2
# ダミー入力 (batch, seq_len, embed_dim)
X = torch.randn(1, seq_len, embed_dim)
(1)
mha = nn.MultiheadAttention(embed_dim, num_heads, bias=False, batch_first=True)
mha.eval() # 評価モードにしてdropoutなどのランダム性を排除
# (2)
torch_output, torch_w = mha(query=X, key=X, value=X, average_attn_weights=False)
説明メモ
- 5×4行列のXを準備します。
- (1) bias項なし、batch_first=Trueで計算します。
- dropoutなどのランダム性も排除したいのでeval()モード
- (2) 自己注意なのでquery=key=valueとします。mhaの内部で$Q, K, V$が計算されます。
- average_attn_weights=Falseとすることで、ヘッド毎に求めたattention weightsをそのまま抽出することができます。Trueだと平均値のattention weightsになるようです。
torch_outputをmhaの出力値、torch_wをヘッド毎のattention_wtightsとします。これらの値を後で比較・確認することになります。
2.2. 内部パラメータを使い「1.2で説明した手順」で計算
mhaの内部パラメータから、行列$W^Q, W^K, W^V, W^O$を抽出します。抽出した行列を利用して、1.2の計算手順を再現していきます。PyTorchでのMultiheadAttentionの動きを確認していきます。
内部パラメータの取得
先程求めたmhaの内部パラメータを取得します。
# mhaの内部パラメータを取得
W = mha.in_proj_weight # (3*embed_dim, embed_dim) W_Q, W_K, W_Vを合わせた大きな行列
E = mha.embed_dim # mhaで利用した分散表現の次元 d_model=4
H = mha.num_heads # mhaで利用したヘッド数 h=2
D = E // H # ヘッド数に分割した時の分散表現の次元 d=2
# W = [W_Q, W_K, W_V]という大きな行列を先頭から順番に3分割
W_q = W[:E]
W_k = W[E:2*E]
W_v = W[2*E:]
行列の形状だけ表示してみました。12×4の行列$W$が4×4のサイズで3個$(W^Q, W^K, W^V)$に分割されていることが確認されます。
W.shape # torch.Size([12, 4])
W_q.shape # torch.Size([4, 4])
W_k.shape # torch.Size([4, 4])
W_v.shape # torch.Size([4, 4])
QKV行列の作成(「QKV」は行列の変数名)
内部パラメータが取得できたので、中身を細かく見ていきます。
分散表現行列XにWを掛けてQ、K、Vを求めてみます。取得したパラメータWとXを使い実際に行列するだけです。
torch.set_printoptions(linewidth=200) # 出力結果がきれいに見えるようにする
QKV = F.linear(X, W)
print(f"QKV shape: {QKV.shape}")
print(f"QKV:\n{QKV}")
行列Wを掛け算して、5×12の行列(QKV)に変換されます。行列Wを論文で言う$W^Q, W^K, W^V$を縦に並べた行列と解釈することで、図1のように左から順番にQ、K、Vと並んでいると考えることができそうです。
QKV shape: torch.Size([1, 5, 12])
QKV:
tensor([[[-1.3839, 0.3560, -0.5477, 0.5145, 1.5560, -0.1749, 1.3026, -0.2896, 1.4396, -0.2397, 0.6415, 1.2935],
[-0.3053, -0.4555, 0.9167, -0.7092, 0.2180, 0.8775, 0.5869, -1.3853, -0.6356, -0.6922, 0.7399, 0.5402],
[ 0.1798, -0.4656, 0.2638, -0.6801, -0.4169, 0.4765, 0.0991, -0.2992, -0.8500, -0.1792, -0.0935, -0.1088],
[-0.8393, 0.6234, -0.7506, -0.4411, -0.1963, -0.0795, 0.0261, 0.1924, -0.3620, 1.1107, -0.1110, 0.4418],
[-0.2403, -0.3683, -0.1956, -0.2543, 0.2528, 0.1956, 0.6195, -0.0164, -0.0104, -0.3045, -0.0634, 0.2639]]], grad_fn=<UnsafeViewBackward0>)
ヘッド毎に分割
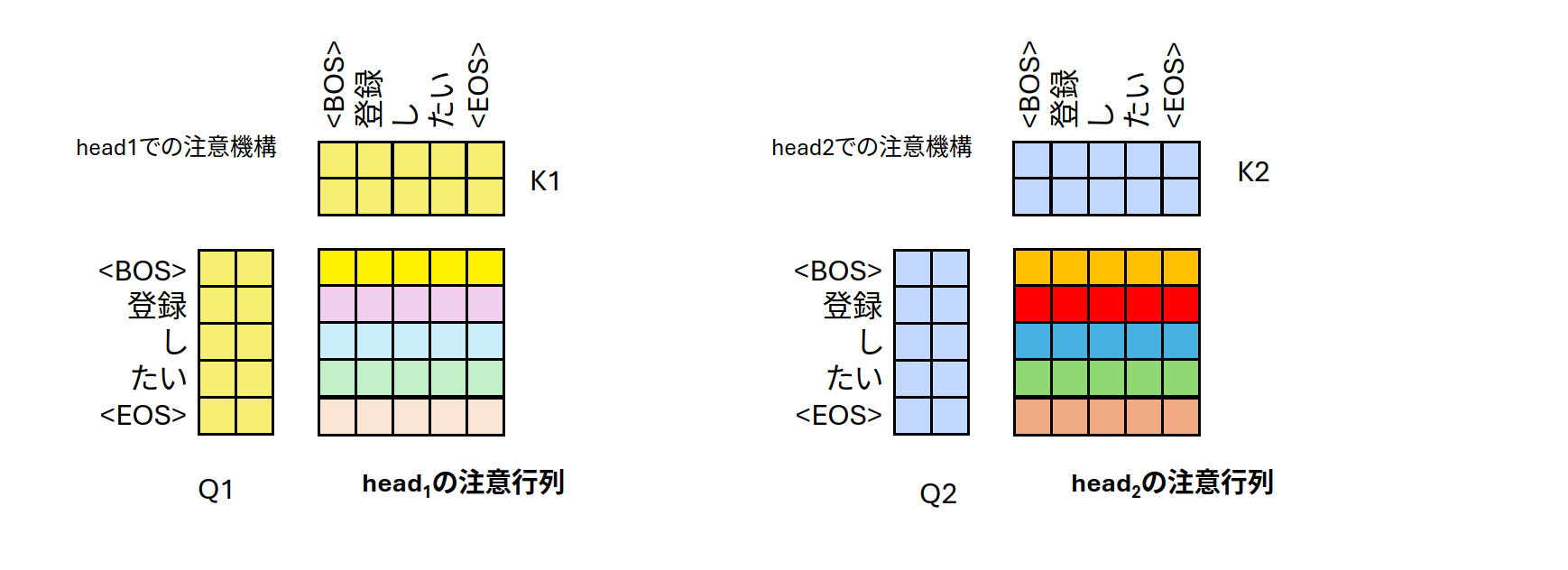
5×12行列のQKVのQ、K、Vに相当する部分をヘッド数で分割します。
QをQ1とQ2に、KをK1とK2に、VをV1とV2に分割します。5×2を6個用意するイメージなので、次のコードで取得できます4。
Q1, Q2, K1, K2, V1, V2 = QKV.view(1,5,3*H,D).transpose(1,2).unbind(dim=1)
説明メモ
- 形状(1, 5, 12)を(1, 5, 6, 2)に変換、5次元の軸 (dim=1) と6次元の軸 (dim=2) を入れ替えます。
- 5×2が6個の形になります。
- unbind(dim=1)を使って、6個をバラバラにします。
Q1:
tensor([[[-1.3839, 0.3560],
[-0.3053, -0.4555],
[ 0.1798, -0.4656],
[-0.8393, 0.6234],
[-0.2403, -0.3683]]], grad_fn=<UnbindBackward0>)
Q2:
tensor([[[-0.5477, 0.5145],
[ 0.9167, -0.7092],
[ 0.2638, -0.6801],
[-0.7506, -0.4411],
[-0.1956, -0.2543]]], grad_fn=<UnbindBackward0>)
Qの部分が[Q1, Q2]となっていることが確認できます。残りも同様です。
分割した(Q1,K1)、(Q2,K2)でのattention weights
ヘッド毎に求めた(Q1,K1)、(Q2,K2)を使ってattention weightsを求めます。
ヘッド$i$のattention weightsは
$$
\text{softmax}(\frac{Q_iK_i^T}{\sqrt{d}})
$$
を計算するだけです。
Q1とK1、Q2とK2を使い、注意行列 (attention weights)を計算します。
# softmax(Q1 K1 /√d)
head1_score = Q1@K1.transpose(-2,-1)/math.sqrt(D)
head1_attn_weights = torch.softmax(head1_score, dim=-1)
# softmax(Q2 K2 /√d)
head2_score = Q2@K2.transpose(-2,-1)/math.sqrt(D)
head2_attn_weights = torch.softmax(head2_score, dim=-1)
mhaによって求められたattention weithgs(変数名:torch_w)と順番に求めた値を比較してみましょう。
tensor([[[[0.0424, 0.2048, 0.3446, 0.2414, 0.1667],
[0.1729, 0.1644, 0.2146, 0.2448, 0.2033],
[0.2667, 0.1591, 0.1675, 0.2068, 0.2000],
[0.0698, 0.2457, 0.3001, 0.2061, 0.1782],
[0.1792, 0.1710, 0.2114, 0.2354, 0.2030]],
[[0.1456, 0.1290, 0.2313, 0.2845, 0.2096],
[0.2896, 0.3155, 0.1334, 0.0994, 0.1622],
[0.2136, 0.3166, 0.1714, 0.1335, 0.1649],
[0.1254, 0.2581, 0.2383, 0.2125, 0.1655],
[0.1764, 0.2372, 0.2087, 0.1930, 0.1846]]]], grad_fn=<ViewBackward0>)
個別に求めた値です。
head1_attn_weights
tensor([[[0.0424, 0.2048, 0.3446, 0.2414, 0.1667],
[0.1729, 0.1644, 0.2146, 0.2448, 0.2033],
[0.2667, 0.1591, 0.1675, 0.2068, 0.2000],
[0.0698, 0.2457, 0.3001, 0.2061, 0.1782],
[0.1792, 0.1710, 0.2114, 0.2354, 0.2030]]], grad_fn=<SoftmaxBackward0>),
head2_attn_weights
tensor([[[0.1456, 0.1290, 0.2313, 0.2845, 0.2096],
[0.2896, 0.3155, 0.1334, 0.0994, 0.1622],
[0.2136, 0.3166, 0.1714, 0.1335, 0.1649],
[0.1254, 0.2581, 0.2383, 0.2125, 0.1655],
[0.1764, 0.2372, 0.2087, 0.1930, 0.1846]]], grad_fn=<SoftmaxBackward0>))
一致していますね ![]() mhaの最終出力(変数名:torch_output)まで求めるには、ヘッド毎のattentionにV1やV2を掛け算、concatして、最後にmha.out_proj.weightで変換する道のりをたどります。ちょっと面倒〜。演習用のコードには記載してあります。
mhaの最終出力(変数名:torch_output)まで求めるには、ヘッド毎のattentionにV1やV2を掛け算、concatして、最後にmha.out_proj.weightで変換する道のりをたどります。ちょっと面倒〜。演習用のコードには記載してあります。
3. 論文ぽい手順
mhaの内部パラメータから求めたW,W_q,W_k,,W_vなどを使い論文の手順で、最終的な出力とヘッド毎のattention weightsを計算していきます。
mhaの内部パラメータでは$Q=XW^Q$を計算する行列$W^Q$が存在しないので$Q=X$とします。$K$や$V$も同様に考えます。
クエリ、キー、バリューをh個(ヘッドの数)用意する
ヘッド数が2個なので、query、key、value用の重み行列を2セットずつ準備します。
# Q, K, Vの作成
Q = X
K = X
V = X
# 小さな行列を先に作成
# mhaのWを利用してQ1などを作成する行列を作ります
W_q1, W_q2 = W_q[:2,:], W_q[2:,:]
W_k1, W_k2 = W_k[:2,:], W_k[2:,:]
W_v1, W_v2 = W_v[:2,:], W_v[2:,:]
# 個別にQiを作成
# ヘッド毎のQ, K, V
Q1 = F.linear(Q, W_q1) # Q1 = Q W_q1^T
Q2 = F.linear(Q, W_q2)
K1 = F.linear(K, W_k1)
K2 = F.linear(K, W_k2)
V1 = F.linear(V, W_v1)
V2 = F.linear(V, W_v2)
ヘッド毎のattentionの計算
head_i = \text{Attention}(Q_i, K_i, V_i) = \text{softmax}(\frac{Q_i K_i^T}{\sqrt{d}}) V_i
を利用してhead1とhead2を求めます。
# softmax(Q1 K1 /√d) V1 の部分
head1_score = Q1@K1.transpose(-2,-1)/math.sqrt(D)
head1_attn_weights = torch.softmax(head1_score, dim=-1)
head1 = head1_attn_weights@V1
# softmax(Q2 K2 /√d) V2 の部分
head2_score = Q2@K2.transpose(-2,-1)/math.sqrt(D)
head2_attn_weights = torch.softmax(head2_score, dim=-1)
head2 = head2_attn_weights@V2
head1_attn_weightsがヘッド1のattention weightsとなります。
ヘッドを集めて、$W^O$を掛け算
\text{MultiHead}(Q,K,V) = \text{Concat}(head_1,…,head_h) W^O
に従い、最終的な出力を求めます。
concat_head = torch.concat([head1, head2], axis=2)
output = F.linear(concat_head, mha.out_proj.weight)
print(torch.allclose(output, torch_output , atol=1e-6))
# True
見た目でも判定してみます。論文での手順で計算したマルチヘッドの出力は次の形になります。
tensor([[[ 0.3529, 0.0220, 0.0969, -0.1303],
[ 0.4565, 0.1399, 0.0720, 0.1694],
[ 0.3354, 0.1571, 0.0336, 0.2145],
[ 0.3725, 0.0816, 0.1403, -0.0746],
[ 0.3248, 0.0932, 0.0436, 0.0879]]], grad_fn=<UnsafeViewBackward0>)
mhaの出力であるtorch_outputは次の形になります。
torch_output:
tensor([[[ 0.3529, 0.0220, 0.0969, -0.1303],
[ 0.4565, 0.1399, 0.0720, 0.1694],
[ 0.3354, 0.1571, 0.0336, 0.2145],
[ 0.3725, 0.0816, 0.1403, -0.0746],
[ 0.3248, 0.0932, 0.0436, 0.0879]]], grad_fn=<TransposeBackward0>)
確認作業は終了となります。
次回
次回はTransformer Encoderによる文章分類で使ったモデルのattention weightsを可視化してみたいと思います。
目次ページ
参考になりそうなサイト
- PyTorchでの説明(様々な状況での計算結果を比較しています)
- Kerasでの説明
可視化も掲載。すごいボリュームです。しかも、定期的に更新されています