🔰PyTorchでニューラルネットワーク基礎 #10【時系列分析・指標計算】

概要

個人的な備忘録を兼ねたPyTorchの基本的な解説とまとめです。LSTMを利用した日経225を利用した予測問題を利用して、第9.5回で登場した時系列分析に関する指標6種類を実際に計算してみたいと思います。第8回で紹介したLSTMのモデルがナイーブモデルと同等、第９回で紹介した４つの特徴量を利用したLSTMのモデルがナイーブモデルよりも良いことが数値的に確認されます

指標

1. モデルの誤差
   • MAE (mean absolute error、絶対平均誤差)
   • RMSE (root mean squared error、二乗平均平方誤差)
   • MAPE (mean absolute percentage error、絶対平均パーセント誤差)
2. 方向性精度
   • MDA (mean directional accuracy、平均方向精度)
3. モデルの比較
   • MASE (mean absolute scaled error、スケール平均絶対誤差)
   • Diebold-Mariano検定（ダイボールド・マリアーノ検定）

演習用のファイル (2025年7月14日　演習ファイルに不具合があったので修正)

• データ：nikkei_225.csv
• コード：sample_10_08.ipynb（第８回のモデル）
• コード：sample_10_09.ipynb（第９回のモデル）

比較するモデル

• モデル１：始値だけを利用したLSTMのモデル（第８回）
• モデル２：始値、高値、安値、終値を利用したLSTMのモデル（第９回）
• ナイーブモデル：１期前の実測値を予測値にするモデル

注意
実際にモデルのパラメータを学習する部分は割愛します。すでに学習済みの状態から記述していきます¹。モデルのパラメータ（重み）は学習のするたびに異なる値となります。これは、重みの初期値がランダムに設定されるためです。同じデータセットを使用しても、以下で求める評価指標のスコアは実行のたびに変動しますので注意してください。

1. 指標の実装

実装といっても、大半がライブラリを使うだけなのでとても簡単です。

利用するライブラリ

• scikit-learn
• dieboldmariano

実測値（観測された値）とモデルの予測値をコード上、次の変数名で表記します。

記号の説明

• real : 実測値
• prediction : モデルの予測値

1.1 モデル誤差に関する指標

実測値のrealと予測値のpredictionの誤差を比較するには、scikit-learnライブラリを利用すると簡単です。Pythonの便利さを感じます。MAPEだけ注意が必要です。％表示にするには100倍する必要があります。
scikit-learnのRegression Metricsに式と使い方の解説が書かれていますので参考にしてください。

基本的な使い方は、scikit-learnの必要な関数を読み込んで、実測値のrealと観測値のpredictionを関数の引数に指定するだけです。

誤差の指標　基本パターン

from sklearn.metrics import (
    mean_absolute_error,             # 平均絶対誤差
    root_mean_squared_error,         # 二乗平均平方誤差
    mean_absolute_percentage_error,  # 平均絶対パーセント誤差
    mean_squared_error,              # 平均二乗誤差
    r2_score                         # 決定係数
)

mae = mean_absolute_error(real, prediction)
rmse = root_mean_squared_error(real, prediction)
mape = mean_absolute_percentage_error(real, prediction)

# ついでにMSEとR2
mse = mean_squared_error(real, prediction)
r2 = r2_score(real, prediction)

print(f"MAE: {mae:.6f}")
print(f"RMSE: {rmse:.6f}")
print(f"MAPE: {mape*100:.6f}%")
print(f"MSE: {mse:.6f}")
print(f"R²: {r2:.6f}")

1.2 方向性精度

方向性精度です。9.5回で紹介した式ではなくてもっと素朴な形でコードにしています　実測値と予測値が同方向なら＋１、異なるなら０としてカウントします。カウントされた値の平均が方向性精度となります。
実測値と予測値のそれぞれの階差を求めて符号の判定をすればOKなので、自作関数を作成してみました。

方向性精度

import numpy as np

# Direction Accuracy関数
#     予測値と実測値の方向性一致率を計算
def direction_accuracy(y_true, y_pred):
    # 前日からの変化方向
    true_direction = np.sign(np.diff(y_true.flatten()))
    pred_direction = np.sign(np.diff(y_pred.flatten()))  
    # 方向が一致した割合
    accuracy = np.mean(true_direction == pred_direction)
    return accuracy

dir_acc = direction_accuracy(real, prediction)

print(f"Direction Accuracy: {dir_acc:.3f} ({dir_acc*100:.1f}%)")

1.3 モデルの比較の指標

MASEはMAEの比率でナイーブモデルとの差を検討する指標でした。こちらもnumpyを使ってベタに実装したほうが、式が見える？と思い、自作関数にしてしまいました²。

MASE

import numpy as np

# 予測モデル、ナイーブモデルのMAEの比率を計算
def mase(y_true, y_pred, y_train):
    mae_pred = np.mean(np.abs(y_true - y_pred))               # モデル予測のMAE
    mae_naive = np.mean(np.abs(y_train[1:] - y_train[:-1]))   # 訓練データを利用したナイーブ予測のMAE（前期の値を使用）
   
    return mae_pred / mae_naive

mase_model = mase(real, prediction, y_train)
mase_naive = mase(real[1:],real[:-1], y_train)

print(f"MASE MODEL: {mase_model:.3f}")
print(f"MASE NAIVE: {mase_naive:.3f}")

最後はDiebold Mariano検定です。2つのモデルの予測精度に統計的有意差があるか否かを検定するものでした。自力実装かと思いきやライブラリがありました

Diebold Mariano検定のライブラリ
pip install dieboldmariano

使い方は簡単で、実測値、モデル１での予測値、モデル２での予測値の３種類を指定すればOKとなります。戻り値は、検定統計量とp値の２つになります。いくつかオプションがありますが、詳細は開発者のページを参考にしてください。

基本的な使い方
dm, p_value = dm_test(actual, f_model, s_model)

テストデータの実測値であるactual、比較する２つのモデルであるf_modelとs_modelの３種類を引数とします。

Diebold Mariano検定

from dieboldmariano import dm_test

actual = real[1:].reshape(-1)          # 実測値
f_model = prediction[1:].reshape(-1)   # モデルでの予測値
s_model = real[:-1].reshape(-1)        # ナイーブモデルでの予測値

# テストを実行
dm, p_value = dm_test(actual, f_model, s_model)

print(f"DM統計量: {dm:.5f}")
print(f"p値: {p_value:.5f}")
print(f"有意水準5%で差があるか: {'Yes' if p_value < 0.05 else 'No'}")

print文、少々凝っていますが、検定統計量とp値、有意水準5%で棄却するかの判定を書いてみました。

2. 実際に計算

2.1 モデル１とモデル２の確認

モデル１は窓サイズ５の始値データから、翌日の始値を予測するモデルです。再帰ネットワークにLSTMを利用しています。

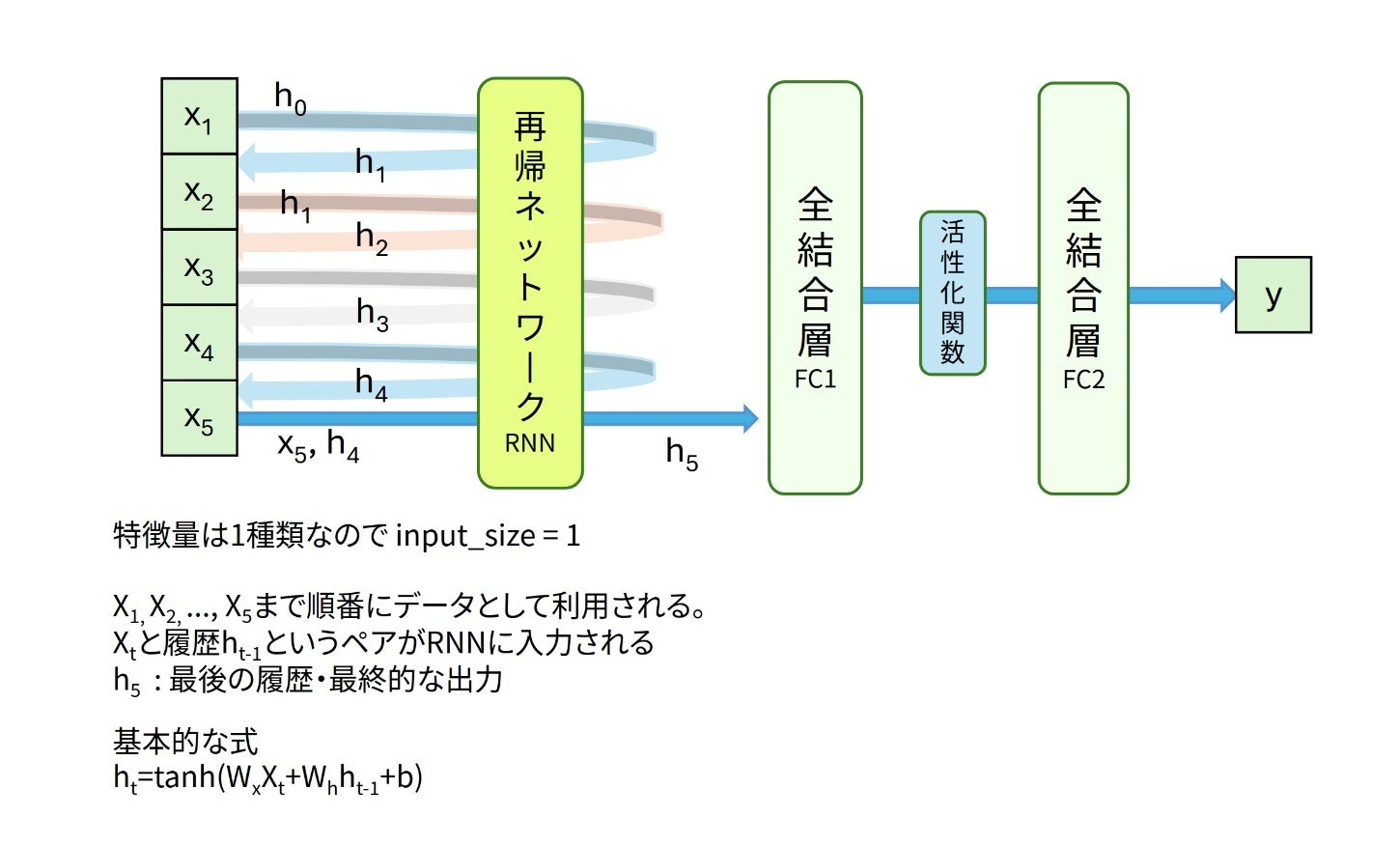図：モデル１

モデル２は窓サイズ５の始値・高値・安値・終値データから、翌日の始値を予測するモデルでした。モデル１と同様LSTMと全結合層で構成しています。

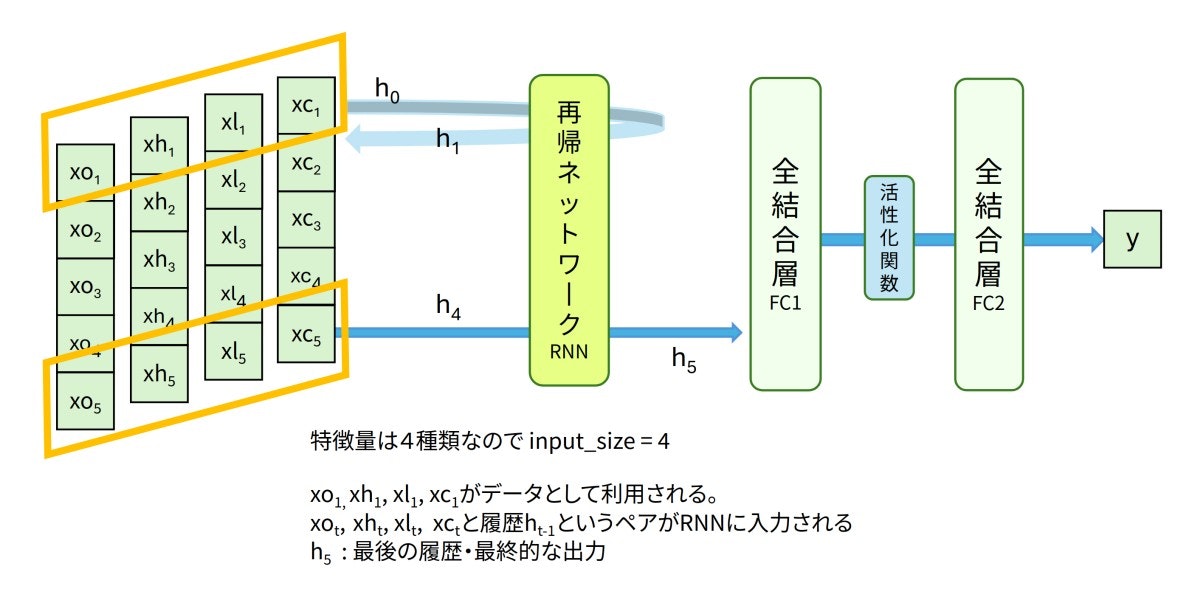図：モデル２

2.2 誤差の指標

表の数値は参考です。ある程度損失が減少している状態なら、大体この数値前後になると思います　今回は日経225を利用した予測で、10,000円で割り算したデータを利用して学習していました。実際に入力されるデータの規模感は2.5〜4くらいになります。平均誤差0.03の解釈は、1万倍して、300円の誤差ということになります。日経225で300円の誤差というのは、若干大きいような気もします。誤差についてはモデル２のほうがモデル１よりも小さいですね。

指標	モデル１	モデル２	ナイーブモデル
MAE	0.0306	0.025738	0.030931
RMSE	0.0417	0.033230	0.041966
MAPE	0.8438%	0.702357%	0.851309%
MSE	0.0017	0.001104	0.001761
R²	0.9449	0.964983	0.943552

1.2 方向性精度

	モデル１	モデル２	ナイーブモデル
方向性精度	0.586 (58.6%)	0.687 (68.7%)	0.571 (57.1%)

モデル１やナイーブモデルはコイン投げで上下を決める（50%）よりは少し良いことがわかります。モデル２は10％ほど改善していますね。でも3割も外すのか〜

1.3 モデルの比較

MASE

	モデル１	モデル２	ナイーブモデル
MASE	1.126	0.915	1.153

モデル１のMASEが１程度ということで、ナイーブモデルと同等の予測性能となります。グラフの見た目を裏切らない結果となりました
モデル２のMASEは１未満なので、ナイーブモデルよりも予測性能が良いことになります。ただ、0.915なので微妙ではありますが　学習回数やパラメータいじると0.8くらいになった気がします。

Diebold Mariano検定
２つのモデルを比較する検定です。モデル１とナイーブモデル、モデル２とナイーブモデルで検定をしました。

	モデル１	モデル２
DM統計量	-0.53549	-2.60777
p値	0.59352	0.00527
有意水準5%で差があるか	No	Yes

こちらもグラフによる見た目判定と同じで、モデル１はナイーブ予測と同等性能ということがわかります。モデル２はナイーブモデルよりも性能が良いことが仮説検定からも支持されています。MASEの値でやや苦戦していたモデル２ですがp値も思いの外、良好でした

次回

これまでは翌日の日経225を予測するタイプでLSTMの使い方を紹介してきました。今度は複数期先まで予測するようなモデルを試してみたいと思います。たしか、系列変換モデルとかEncoder-Decoderモデルと呼ばれていた気がします

注

1. モデルの学習部分については８回、９回を参考にしてもらえると幸いです ↩

2. 探せばライブラリもあると思います。maseというライブラリは multivariate anomaly simulation engine となっていて、目的が異なるようです。注意が必要ですね。 ↩