LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@AzukiImo

🔰PyTorchでニューラルネットワーク基礎 #17 【分位点回帰】

Posted at

概要

個人的な備忘録を兼ねたPyTorchの基本的な解説とまとめです。

分位点回帰は、目的変数の条件付き分布における特定の分位点を推定する統計手法です。Pythonだとstatsmodels.apiを利用することで、分位点回帰を簡単に実装することができます（参考）。当然ですが、通常のアプローチでは線形モデルが適用され、非線形関係や交互作用を適切に捉えるには分析者による試行錯誤が不可欠となります。

分位点回帰にもニューラルネットワークを活用することで、モデルの設計負担を軽減し、データから自動的に最適な関数形を学習させることが可能になります。ニューラルネットワークの表現力により、線形モデルや単純な非線形モデルでは捉えきれない複雑な関係を学習できそうです。その代わり解釈が難しくなるのですが:sweat_smile:

今回は、ニューラルネットワークベースの分位点回帰について演習を行ってみます:cactus:

方針

  1. できるだけ同じコード進行
  2. できるだけ簡潔（細かい内容は割愛）
  3. 特徴量などの部分，あえて数値で記入（どのように変わるかがわかりやすい）

演習用のファイル

1. 分位点回帰の損失関数

ニューラルネットワークを利用して分位点回帰を行うには、分位点回帰に対応した誤差関数で学習させる必要があります。分位点回帰の誤差関数から確認していきます。詳しくは「分位点回帰の基本的なところ」を参考にしてください。数学的な解説もあり非常に感動:heart_eyes:

1.1 損失関数

教師データである実測値（観測値）を$[~t_1,...,t_i,...,t_n~]$、モデルからの対応する予測値を$[~y_1,...,y_i,...,y_n~]$とします。

記号

  • $t_i$ : $i$番目の実測値（教師データ）
  • $y_i$ : $i$番目の予測値

OLS回帰分析での損失関数（誤差関数）は、（平均）二乗誤差を利用しました。

\frac{1}{n}
\sum_{i=1}^{n}(t_i - y_i)^2

分位点回帰での損失関数は、分位点$\tau$について、

\frac{1}{n} \left[~
\sum_{t_i \ge y_i} \tau | t_i - y_i | + \sum_{t_i < y_i} (1-\tau) | t_i - y_i | 
~\right]

という分位点の重み付き絶対誤差の平均値を利用します1。

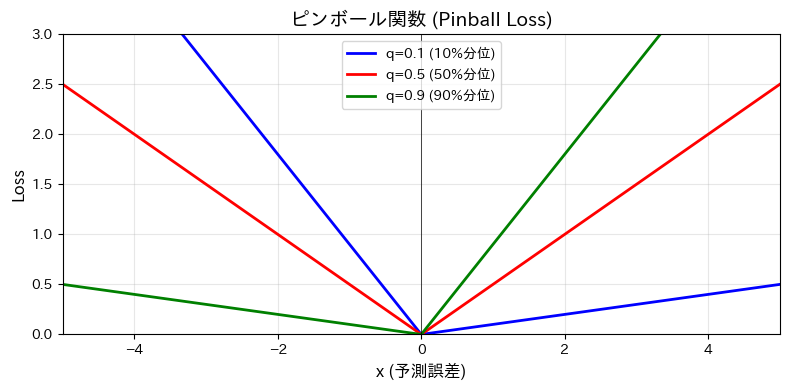
1.2 Pinball関数

分位点回帰の損失関数はピンボール関数と呼ばれ、ボールが非対称に跳ね返るような形の関数をしています。

L_{\tau}(t-y) = \left\{
\begin{array}{ll}
\tau (t-y)     & if~ t-y\ge0 \\
(\tau-1)(t-y)  & if~ t-y < 0
\end{array}
\right.

図：ピンボール関数（τ=0.1、0.5、0.9で描画）
image.png

条件部分をまとめると、

L_{\tau}(t-y) = \max\Bigl\{ \tau(t-y),~(\tau-1)(t-y)\Bigr\}

の形になります。

ピンボール関数をすべての教師データ$t_i$と予測値$y_i$について、足し合わせると

\sum_{t_i \ge y_i} \tau | t_i - y_i | + \sum_{t_i < y_i} (1-\tau) | t_i - y_i |

もしくは、

\sum_{i=1}^{n}L_{\tau}(t_i-y_i) = \sum_{i=1}^{n}\max\Bigl\{ \tau(t-y),~(\tau-1)(t-y)\Bigr\}

となります。

ニューラルネットワークでの損失関数にピンボール損失関数を利用することで分位点回帰になります。大きく変更される部分は、損失関数の設定となります。

追加項目

  • 損失関数のクラスを作成する。
  • ピンボール損失関数クラスを作成、ニューラルネットワークの学習に利用する。

今回は、スポーツ飲料の販売指数と平均気温のデータを利用したのニューラルネットワークによる分位点$\tau_1$、$\tau_2$、$\tau_3$での回帰の演習となります。

2. コードと解説

PyTorchによるプログラムの流れを確認します。基本的に下記の５つの流れとなります。Juypyter Labなどで実際に入力しながら進めるのがオススメ

  • データの読み込みとtorchテンソルへの変換　(2.1)
  • ネットワークモデルの定義と作成　(2.2)
  • 誤差関数と誤差最小化の手法の選択　(2.3)　ここが大きく変わる部分
  • 変数更新のループ　(2.4)
  • 検証　(2.5)

2.0 データについて

データの準備は簡単です。ダウンロードしてCSVファイルとして保存すればOKです。

手順

  1. 【気象庁共同プロジェクト】気象データのビジネス活用の「元データのダウンロード」からダウンロードします。ファイル名はDL4.xlsとなっています。
  2. 「東京都時系列スポーツ飲料データ」タブを選択してCSVとして保存すれば終了です。
  3. 　CSVファイルは、dataフォルダにsports_temp.csvとして保存しました。

2.1 データの読み込み

データの読み込みと分割
# 1. ライブラリの読み込み
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.model_selection import train_test_split

# 2. pandasでCSVファイルを読み込む
df = pd.read_csv("./data/sports_temp.csv")

# 3. train_test_splitで分割
# デバイスの選択
device = "cuda:0" if torch.cuda.is_available() else "cpu"
print("Using Device Name:", device)

x = df["平均気温"]
t = df["販売指数"]

# torchテンソルに変換
x = torch.FloatTensor(x).view(-1,1).to(device)
t = torch.FloatTensor(t).view(-1,1).to(device)

x_train, x_test, t_train, t_test = train_test_split(x, t, random_state=55)

pandasでCSVファイルを読み込んで、train_test_splitで推定につかう訓練用データと検証用のテストデータとに分割します。

x_trainとt_trainが推定に利用されるデータになります。x_trainを説明変数に、t_trainを目的変数（教師データ）として 学習させます。

2.2 ネットワークモデルの定義

ネットワーク構造は素朴な非線形の回帰モデルのように、全結合層（線形層）を活性化関数でつないでいるだけです。１つだけ注意点があります。
平均気温という１つのデータから、３つの分位点に合わせた予測値を出力する必要があるので、全結合層の最終出力は３となります。

image.png

全結合層と活性化関数を利用してシンプルに非線形モデルを設計できるネットワーク構造になっています:four_leaf_clover:

ネットワーク構造
# 分位点の設定
quantiles = [0.1, 0.5, 0.9]

# ネットワーク構造
class DNN(nn.Module):
    def __init__(self):
        super(DNN, self).__init__()
        self.fc1 = nn.Linear(in_features=1, out_features=8)
        self.bn1 = nn.BatchNorm1d(8)
        self.act1 = nn.Sigmoid()
        self.fc2 =  nn.Linear(in_features=8, out_features=3)

    def forward(self, x):
        h = self.fc1(x)
        h = self.bn1(h)
        h = self.act1(h)
        y = self.fc2(h)
        return y       
model = DNN()
model.to(device)

コードのポイント

  • 分位点には「0.1、0.5、0.9」を利用
  • 線形層を活性化関数で接続しているだけ
  • バッチ正規化層のBatchNorm1dを使わなくてもOK
  • nn.Linearの最終出力を３（分位点の個数）に設定

いよいよ誤差関数の定義になります:sweat:

2.3 誤差関数と誤差最小化の手法の選択

「回帰モデルなので、誤差関数に平均二乗誤差を指定」とならないので注意です。誤差関数にピンボール損失関数を利用する必要があります。

例 1. 誤差関数の具体的な計算例

入力するデータが1種類、教師データが1種類、分位点は0.2と0.8の2種類を考えます。表の状況でピンボール損失関数を利用した誤差を実際に計算してみましょう。ピンボール損失関数は次のような形でした。

L_{\tau}(t_i - y_i) = \left\{
\begin{array}{ll}
\tau (t_i - y_i)     & if~ t_i - y_i\ge0 \\
(\tau-1)(t_i - y_i)  & if~ t_i - y_i < 0
\end{array}
\right.
データ１ データ２
入力(x) 5 10
教師(t) 100 200
τ₁=0.2での予測値(y) 80 190
τ₂=0.8での予測値(y) 120 220

入力するデータ(x)は１種類、出力される値は、分位点τ₁での予測値と分位点τ₂での予測値の２種類です。観測したデータはデータ１とデータ２の２個とします。

τ₁=0.2での損失から計算します。τ₁でのピンボール関数（重み付き絶対誤差）の平均値を求めます。

τ₁=0.2での損失

L_{\tau_1}(t,y)=
\frac{1}{2}\Bigr(
0.2\times(100-80) + 0.2\times(200-190)
\Bigr)
= \frac{1}{2}(4+2)
= 3

τ₂=0.8での損失を計算します。データ1、データ２での予測値と教師データの誤差を求めて平均を計算することになります。

τ₂=0.8での損失

L_{\tau_2}(t,y)=
\frac{1}{2}\Bigl(
-0.2\times(100-120) + (-0.2)\times(200-220)
\Bigr)
= \frac{1}{2}(4+4)
= 4

τごとの損失が求まりました。あとはニューラルネットワークで学習できるように損失を一つの値にまとめます。

最終的な損失の値
分位点と予測値の順序を揃えるために順序ペナルティを課すなどいくつかパターンがあるのですが、今回は単純に$L_{\tau_1}(t,y)$と$L_{\tau_2}(t,y)$の平均値で計算例を求めます2。

損失 
= \frac{1}{2}L_{\tau_1}(t,y) + \frac{1}{2}L_{\tau_2}(t,y)
= \frac{3}{2} + \frac{4}{2}
= \frac{7}{2}

例1で求めた損失の計算をコード化すればOKです。

損失関数の作成

ピンボール損失関数クラス
# 損失関数のクラスと定義
class PinballLoss(nn.Module):
    def __init__(self, quantiles, device="cpu"):
        super().__init__()
        self.quantiles = torch.FloatTensor(quantiles).to(device)
        
    def forward(self, pred_values, actual_values):
        error = actual_values - pred_values

        # ピンボール損失の計算: max(τ*(t-y), (τ-1)*(t-y))
        M = torch.max(self.quantiles * error, (self.quantiles - 1) * error)
        loss = M.mean()   # 損失の平均値
        return loss

コードのポイント

  • 分位点を与えるリストquantilesをdevice対応のテンソルに変換します。
  • M=torch.max(...)の行が１.2で紹介したピンボール関数の計算部分になります
  • M.mean()で一気に平均値を計算しました
誤差関数
criterion = PinballLoss(quantiles=quantiles, device=device)
optimizer = torch.optim.Adam(model.parameters())

コードのポイント

  • PinballLoss() を利用して損失関数を設定
  • 回帰モデルといえば、nn.MSELoss() だったけど今回は違うぞ

2.4 変数更新のループ

学習用に作成したx_trainと教師データt_trainを使って変数をアップデートしていきます。

変数の更新
LOOP = 3000

model.train()
for epoch in range(LOOP):
    optimizer.zero_grad()
    y = model(x_train)
    loss = criterion(y,t_train)
    if (epoch+1)%200 == 0:
        print(epoch,"\tloss:", loss.item())
    loss.backward()
    optimizer.step()

# 199: loss: 0.15186108648777008
# 399: loss: 0.08311977237462997

LOOPの回数は適当ですので、損失の減少具合で適宜判断してください:smile:

2.5 検証

予測値の計算
model.eval()
np_temp_range = np.linspace(df["平均気温"].min(), df["平均気温"].max(), 100)
temp_range = torch.FloatTensor(np_temp_range).view(-1,1).to(device)

with torch.inference_mode():
    pred = model(temp_range)
pred = pred.detach().cpu().numpy()

コードのポイント

  • model(気温)で3種類の予測値が求まります。
  • グラフをきれいに描画するために、平均気温の最低値〜最大値の範囲を100分割したデータを入力値として使います。
  • 予測値predはmatplotlibで描画するためにnumpyに戻しておきます。

グラフ表示

可視化
np_x_test = x_test.detach().cpu().numpy()
np_t_test = t_test.detach().cpu().numpy()

fig, ax = plt.subplots(figsize=(6,4))

# テストデータを散布図としてプロット
ax.scatter(np_x_test, np_t_test, color="skyblue", label="テストデータ", alpha=0.6)

# 分位点ごとの予測値
for i, t in enumerate(quantiles):
    # 予測曲線をプロット
    ax.plot(np_temp_range, pred.T[i], label=t)
# グラフのタイトルとラベルを設定
ax.set_title("ニューラルネットワークモデルのフィット")
ax.set_xlabel("平均気温")
ax.set_ylabel("販売指数")
ax.legend()
plt.show()

image.png

本来は0.1以上0.9以下にテストデータがあるのかどうかで割合を計算すればいいのですが、ここは、見た目判定:sweat_smile: 0.1〜0.9の間である80%区間にテストデータも収まっているように見えるかな？微妙なきもします:sweat_smile:

気温から販売指数を予測してみた

販売指数を具体的な数値でチェックしてみましょう。

代表的な値で求めてみた
# 代表的な気温を入力データとして準備
temp = torch.FloatTensor([[20],[25],[30],[35],[40]]).to(device)   # FloatTensorだよ
prediction = model(temp)    # model(temp)で予測値が計算される。出力は３種類（分位点0.1〜0.9）

# 表の形で出力してみた
pred_df = pd.DataFrame(temp.detach().cpu().numpy(), columns=["気温"])
pred_df[["悲観的(0.1)","通常(0.5)","楽観的(0.9)"]] = pd.DataFrame(prediction.detach().cpu().numpy())
print(pred_df)
気温 悲観的(0.1) 通常(0.5) 楽観的(0.9)
20.0 0.788900 1.062313 1.393680
25.0 1.325872 1.683748 2.057495
30.0 2.338599 2.651761 2.971779
35.0 3.141405 3.414234 3.684154
40.0 3.528803 3.809758 4.066600

現在の販売状況と気温から予測シナリオを考えることもできます。ただし、学習結果ごと値が異なるので注意かも:cactus:

📈販売が好調なケース（楽観的に予測）

  • 30度：2.9の販売指数予測

📉販売が低調なケース（悲観的に予測）

  • 30度：2.3の販売指数予測

平均気温40度だとあつすぎて屋外にいないので販売が低迷？とか有り得そうだけど、どの予想でも販売指数は増加している。

次回

いろいろ試したいことがあるので、どうなるのかわかりませんが、予測値に幅をもたせる方向か？因果畳み込みによる時系列分析の続きあたりかな。

目次ページ

注

  1. 平均値を求めるための定数倍である1/n倍を考慮しなくても学習することは可能です。 ↩

  2. 推定する異なる分位点の値が分位点0.1と分位点0.15のように近い場合、予測値の大小関係と分位点の大小関係が交差する可能性があるようです。 ↩

1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?