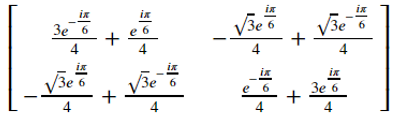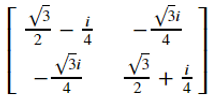量子コンピューターのAdvent Calendar19日目の記事になります。
さて、昨日のDave氏の時間を進めるシミュレーションの記事に続いて、今度はそれを逆向きに戻しちゃおうと思います!
誇大広告のようなタイトルですが、2017年にプレプリントサーバーであるarXivに投稿された論文を自分なりに解釈し、実装してみました。行間や数式を埋めて実装してみると、そもそもの量子アルゴリズムの実装はどう考えて、どんな感じで組み立てるのか、ということが勉強になったので、それらを記録する意味でもこの記事を書いています。
今回対象とした原論文はこちらになります。
[「Arrow of time and its reversal on IBM quantum computer」(arXiv:1712.10057)]
(https://arxiv.org/abs/1712.10057)
本気出し過ぎて、丁寧に補足を書いていたら、恐ろしく長くなったので、時間をかけて読まれるとよろしいかと思います。
なぜこの論文を読んだの?
単純に現象として面白そうで、元理論物理屋の血が騒いだという他ありません。
そして、時間を戻せるならタイムマシンでも作って、あの日の自分を叱りつけてやりたいのですが、今のところそういったことが起こった記憶がないので、未来の自分ではタイムマシンは作れなかったのでしょう。残念。まあ、SERNとかラウンダー、ロシアとかアメリカに狙われないだけマシと思うことにします。
注:SERNは某科学アドベンチャーシリーズに出てくる、架空の研究機関です。読み方は一緒です。
数学的前置き
この論文を読む上では、数式が当然重要になります。ポイントを整理していきましょう。
複素数と複素共役
この論文の最大のポイントとなるのは「複素共役」です。
量子コンピューター(ひいては量子力学)は複素数で表現されるのだ!という話はどこかで聞いたことがある方も多いと思います。しかし、いざ勉強してみると、それほど複素数を意識する場面は少なかったのではないでしょうか。
DeutschやGroverのアルゴリズムでは、(表立って)複素数が登場する場面はありませんでした。わかりやすい所だとQFT(Quantum Fourier Transformation)ぐらいかと思います。
しかし、一般の量子状態は、複素数で表現されています。今回はそうなるような状況をワザと作った上で、時間を逆流させることになります。
詳しくはこちらに記載しているので、ご覧ください。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
指数行列
今回は自然対数の底$e$の肩に行列を乗せる形で表現する数式が出てきます。
まず$e^x$の定義に戻る必要があります。こんな感じに定義しています。$x$は実数でも複素数でも良いです。
e^x = 1+ \frac{x}{1!}+ \frac{x^2}{2!} + \cdots + \frac{x^n}{n!} + \cdots = \sum_{n=0}^{\infty} \frac{x^n}{n!}
実は、このxは行列に拡張することができます。行列を$A$としたら、次のように定義できます。
e^A = 1+ \frac{A}{1!}+ \frac{A^2}{2!} + \cdots + \frac{A^n}{n!} + \cdots = \sum_{n=0}^{\infty} \frac{A^n}{n!}
単純に$x$を$A$に置き換えてみたってだけです。ただ、これは行列なので、具体的な計算をする場合には、行列の掛け算で求めていく必要があります。
物理の準備
今回は物理現象に重きを置いたアルゴリズムということもあり、シュレディンガー(Schrödinger)方程式が登場します。
では、これについて少し解説します。
シュレディンガー方程式と複素共役と時間反転
シュレディンガー方程式は、量子状態 $ \ket{\psi} $があり、その物理系のハミルトニアンを$\hat{H}$としたとき、次のように記述されます。
i\hbar \frac{\partial \ket{\psi} }{\partial t} = \hat{H} \ket{\psi}
$i$は虚数で、$\hbar$はプランク定数と呼ばれる、量子力学の世界で重要になる定数です。ここでは、そんな数字があるという風に思っていれば、十分です。
問題は、この方程式をどう解釈するか、です。
量子状態$ \ket{\psi} $を時間$t$という変数で、偏微分しているのですが、これは量子状態が時間とともにどう変化していくかを教えてくれる方程式です。
となると、この記事の本題である、時間との関連性があることがわかってきますね。え?そんな風に見えない?
もう少し理解を進めやすくするために、量子状態は$ \ket{\psi} $は何らかのベクトルであり、その成分は複素数になっています。また、$\hat{H}$は行列と考えていくことができます。
ここで、シュレディンガー方程式全体を複素共役を取ってみます。そうすると・・・
-i\hbar \frac{\partial \ket{\psi^*} }{\partial t} = \hat{H} \ket{\psi^*}
と書けます。複素共役は、虚数$i$がついている部分の符号を入れ替えるというルールに沿って機械的に処理しています。また、量子状態$\ket{\psi^*}$の中身は良くわからないですが、何らかの複素数で表現されており、それぞれが複素共役を取った状態になったものを、このように書いておくことにします。
では、これの見方を修正してみます。
i\hbar \frac{\partial \ket{ \psi^*} }{\partial (-t)} =\hat{H} \ket{\psi^*}
偏微分の$t$となっている箇所を$-t$に置き換えました。これは何を意味するでしょうか。見ていると元に式にとてもよく似ていますね。$t$符号がプラスのときは、単純に時間が前に進むのと同じですが、符号を逆転させると時間が逆向きに進むことを意味するように解釈できます。え?やっぱり、そんな風に見えない?ま、まあ、いいでしょう。
まとめると、上記の式は時間を$-t$方向に進める、言い換えれば時間を巻き戻す方向に進めるときに、量子状態$\ket{\psi^*}$がどう変化するかを教えてくれる方程式であるのです。
Hの複素共役についての補足(読み飛ばしても大丈夫です)
ハミルトニアン$\hat{H}$も複素共役を取られているのですが、実は中身は変わっていません。これは、$\hat{H}$に対する物理的要請によって、複素数をとっても形が変わらない構造であるように取り決めています。
少し専門用語で話すと、エルミート行列と呼ばれるものです。
また、$\hat{H}$は対象とする量子系のエネルギーを決めるための演算子(数学的には行列と同じ)で、物理量は実数であるべし、という強い要請から、$\hat{H}$はエルミート行列でなければいけないというルールがあります。この辺は、量子物理学の前提に関わる話なので、そういうルールであると思っていいただければ大丈夫です。
理論と実装方針の解説
さて、では理論を概説していきます。細かい計算式やそれらの導出は端折りますので、興味のある方は原論文を読んでください。
全体の流れは以下のようになっています。わかりやすい(?)イメージとしては、ビリヤードの上で玉を転がすシーンを思い浮かべてみてください。

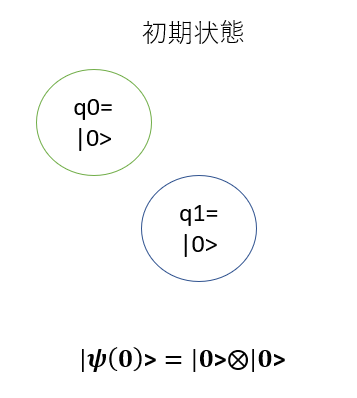
1.初期状態の準備する
これ自体は、特にどうってことのないことです。
まずは、任意の状態で大丈夫です。以下では、話を簡単にするために、全ての量子ビットが$\ket{0}$としておきます。
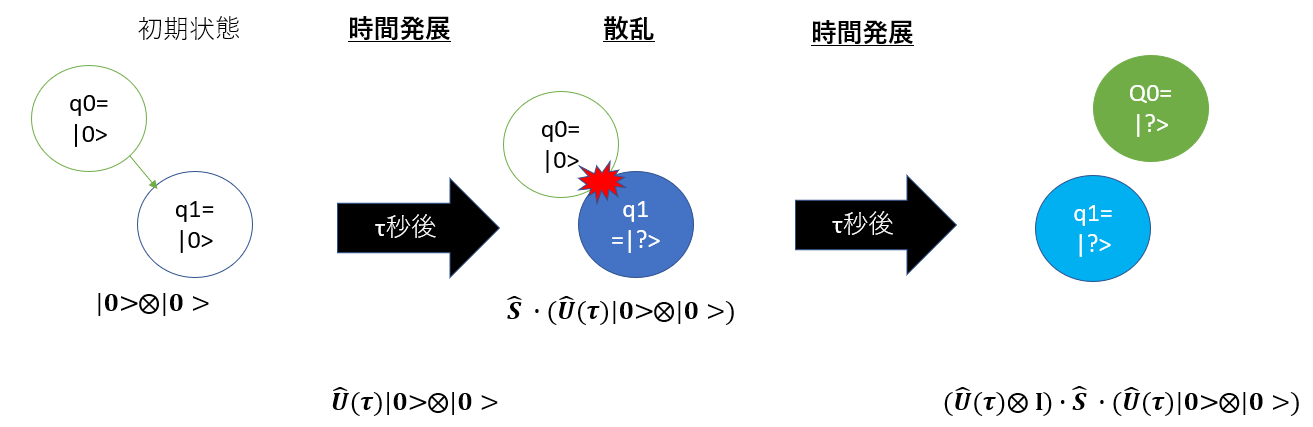
2.状態を掻き乱す
ここでは、以下のようなことをします。
2-1.シュレディンガー方程式に従って初期状態から時間発展させる
まずこの論文で使われているハミルトニアン$\hat{H}$は、以下のものを想定しています。
\begin{align}
\hat{H} = \hbar\omega(\hat{Z}\cos{\alpha} + \hat{X}\sin{\alpha} ) = \hbar\omega
\begin{pmatrix}
\cos{\alpha} & \sin{\alpha} \\
\sin{\alpha} & -\cos{\alpha}
\end{pmatrix}
\end{align}
$\hat{X}$と$\hat{Z}$は、それぞれパウリ演算子のXとZです。また、今の時点では$\omega$と$\alpha$は不定のパラメーターですが、実装の際には任意の値を入れれば、好きなように時間発展させられます。実験においては、適当な値を代入して計算させています。
また、このハミルトニアンがエルミートであることは簡単に確認できます。(線形代数の練習です)
さて、これを使いたのですが、もう一つ準備が必要です。先ほど挙げた、シュレディンガー方程式は、ハミルトニアンが時間発展しないケースにおいては、簡単な微分方程式となって解くことができます。$\ket{\psi(0)}$を初期状態として、t秒間時間発展した状態を$\ket{\psi(t)}$とすると・・・
i\hbar \frac{\partial \ket{\psi} }{\partial t} = H \ket{\psi} → \ket{\psi(t)} = e^{-\frac{i\hat{H}t}{\hbar}} \ket{\psi(0)}
はい、これでやっと準備した内容が繋がってきました。$e^{-\frac{i\hat{H}t}{\hbar}}$の部分は、$\hat{H}$という行列が乗っかった指数行列の形になっていることが読み取れます。($i$とか$\hbar$とか$t$とかは単なる定数と同じ)
この行列の構造が具体的に求めておき、それを何らかのゲートたち(=行列の積)で表現することができれば、量子コンピューターで実装できる、という流れになります。
このゴールを忘れないようにしてください。
時間発展演算子を具体的に求めてみる
では、パラメーターに値を代入して、具体的にどうやって求めるのかを考えていきます。
まずは、初期状態$\ket{\psi(0)}$の前にかかっている、演算子に着目して、今回使用するハミルトニアンの具体的な構造を入れてみます。
e^{-\frac{i\hat{H}t}{\hbar}} = e^{-i\omega\tau
\begin{pmatrix}
\cos{\alpha} & \sin{\alpha} \\
\sin{\alpha} & -\cos{\alpha}
\end{pmatrix}}
ここで、$\omega\tau=\pi/6$、$\alpha=\pi/3$としてみます。すると・・・
\begin{align}
e^{-i\frac{\pi}{6}
\begin{pmatrix}
\frac{1}{2} & \frac{\sqrt{3}}{2} \\
\frac{\sqrt{3}}{2} & -\frac{1}{2}
\end{pmatrix}}
=
e^{-i
\begin{pmatrix}
\frac{\pi}{12} & \frac{\sqrt{3}\pi}{12} \\
\frac{\sqrt{3}\pi}{12} & -\frac{\pi}{12}
\end{pmatrix}}
\end{align}
=\sum_{n=0}^{\infty} \frac{(-i)^n}{n!} \begin{pmatrix}
\frac{\pi}{12} & \frac{\sqrt{3}\pi}{12} \\
\frac{\sqrt{3}\pi}{12} & -\frac{\pi}{12}
\end{pmatrix}^n
詰んだ・・・。これを見てもっと簡単な形にできることを見抜ける人がいたら、人間辞めたレベルの人なので、ご注意ください。
ただ、ちょっとSymPy先生のお力を借りると、すぐに求めることができてしまいます!SymPyすごい!(SymPyは、代数計算を行うためのPythonライブラリです)
こんな感じで書きます。
i=sym.I
X = sym.Matrix([
[0, 1],
[1, 0]
])
Z = sym.Matrix([
[1, 0],
[0, -1]
])
H = -1*i*(Z*sym.cos(alpha)*omega_tau + X*sym.sin(alpha)*omega_tau)
expH = H.exp()
お!思ったよりも簡単な形になったぞ!ただ、もう少し使いやすい形にしたいところです。
ちょっとしたポイントがあって、途中で実部と虚部に一度分解してから、再度くっつけるように計算するようにしました。
こんな感じ
H = -1*i*(Z*sym.cos(alpha)*omega_tau + X*sym.sin(alpha)*omega_tau)
expH = H.exp()
re = sym.re(H.exp())
im = sym.im(H.exp())
re+im
なんか拍子抜けするくらい簡単になっちゃったw
ここまで来れば、手で検算も可能になるレベルですね。
具体的に求まった行列を量子コンピューターに実装するには
さて、実装するにはこの行列を何らかの量子ゲートを使って表現する必要があるのですが、どうすれば良いでしょうか。
ここではタイトルの通りに、IBM Qだとどうできるか、で説明します。
まず、使えるゲートは以下の通りです。

全部を説明すると紙面がえらいことになるので、説明のページを読んでてみください。
https://quantum-computing.ibm.com/support/guides/gate-overview?section=5d00d964853ef8003c6d6820
ここでは、結論だけを書きます。答えは、U3ゲートを使うことで、解決します。
U3ゲートは、3つのパラメーターだけを使って、**任意の1量子ビットユニタリ演算子(行列)**を作ることができます。言い換えると、この3つのパラメーターが求まれば、どんな1量子ビットのゲートを作れることができます。すごいですね!
では、そのパラメーターたちを求めるには、どうしたらいいでしょうか。まずはU3の行列構造を理解する必要があります。
今回求めたい時間発展の演算子を$\hat{U}$としましょう。すると、、、
\begin{align}
\hat{U} = e^{i\delta}\hat{U}_3(\theta,\chi,\xi)
=
e^{i\delta}
\begin{pmatrix}
\cos{\frac{\theta}{2}} & -e^{i\xi} \sin{\frac{\theta}{2}} \\
e^{i\chi} \sin{\frac{\theta}{2}} & e^{i(\chi+\xi)}\cos{\frac{\theta}{2}}
\end{pmatrix}
\end{align}
となります。$\delta$はグローバル位相なので、量子状態には影響を与えないのですが、手計算上では必要なので残しておきました。これに合わせた形に、先ほどの時間発展演算子を変形してみます。これは複素数と行列の計算練習になるので、計算力を身に着けたい方はやってみてください。ここでは結果だけ書きます。
\begin{align}
\hat{U} =
e^{i\delta}
\begin{pmatrix}
\cos{\frac{\theta}{2}} & -e^{i\xi} \sin{\frac{\theta}{2}} \\
e^{i\chi} \sin{\frac{\theta}{2}} & e^{i(\chi+\xi)}\cos{\frac{\theta}{2}}
\end{pmatrix}
=
e^{i\delta}
\begin{pmatrix}
\frac{\sqrt{13}}{4} & e^{i\chi} \frac{\sqrt{3}}{4} \\
e^{i\chi} \frac{\sqrt{3}}{4} & e^{2i\chi}\frac{\sqrt{13}}{4}
\end{pmatrix}
\end{align}
e^{i\delta}=\sqrt{\frac{12}{13}}-\frac{i}{\sqrt{13}}
e^{i\chi} = e^{-i\frac{\pi}{2}}(\sqrt{\frac{12}{13}}+\frac{i}{\sqrt{13}})
式を見比べて、$\theta$と$\chi$を求めます。($\xi$については、考えている行列の非対角成分が等しい対称行列なので、$\xi=\chi+\pi$とおけるので、これを特別求める必要はありません。)
\cos{\frac{\theta}{2}} = \frac{\sqrt{13}}{4} → \theta = 2\cos^{-1}( \frac{\sqrt{13}}{4}) \approx 0.896
\sin{\chi} = -\frac{1}{\sqrt{13}} → \chi = \sin^{-1}( \frac{1}{\sqrt{13}}) - \frac{\pi}{2} \approx -1.290
長い旅路の果てにやっと求まりました。ここで、出た角度を入れれば時間発展演算子の実装ができます。
あくまでこれはパラメーターを具体的に定めてもとめたものです。ただ、パラメーターの値が変わったとしても、考え方は同じです。いろいろパラメーターを変えて求めた結果は、以下になりますが、上記の考え方で一致していたので、論文と同じところまでは辿り着けました。
コードは、こんな感じに書きました。これはあくまでもこの論文の設定(ハミルトニアン)にしか通用しないので、ご注意ください。
def TimeEvolution(qubits,omega_tau,alpha):
H = -1*i*(Z*sym.cos(alpha)*omega_tau + X*sym.sin(alpha)*omega_tau)
expH = H.exp()
re = sym.re(H.exp())
im = sym.im(H.exp())
theta = np.arccos(float( sym.sqrt( re[0,0]**2 + im[0,0]**2 )))*2
xi = np.arcsin(float( -1*im[0,0] / sym.sqrt( re[0,0]**2 + im[0,0]**2 ) )) - np.pi/2
qubits.u3(theta,xi,xi+np.pi,1) # This Operator is symmetry.
return qubits
| $\omega\tau$ | $\alpha$ | $\theta$ | $\chi$ |
|---|---|---|---|
| $\frac{\pi}{6}$ | $\frac{\pi}{6}$ | 0.505 | -1.107 |
| $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | 0.723 | -1.183 |
| $\frac{\pi}{6}$ | $\frac{\pi}{3}$ | 0.896 | -1.290 |
| $\frac{\pi}{6}$ | $\frac{\pi}{2}$ | $\frac{\pi}{3}$ | -$\frac{\pi}{2}$ |
2-2.ビリヤードの球がぶつかった(物理的には散乱と呼ばれる現象が発生した)こと2量子ビットに相互作用が起こり
ここでは散乱を表す(エルミート)演算子$\hat{S}$を以下のように与えることにします。(論文まま)
\hat{S} = \ket{0}\bra{0} \otimes \hat{S}_0 + \ket{1}\bra{1} \otimes \hat{S}_1
これの意味を説明すると、「片方量子ビットの状態が$\ket{0}$なら残りの量子ビットに$ S_0 $を作用させなさい、一方で状態が$\ket{1}$なら残りの$S_1$を作用させなさい」、と言ってるに過ぎないのです。
ん?ちょっと待てよ!これって、少し見方を変えられるのではないだろうか?
片方の量子ビットの状態に応じて、もう片方の量子状態に演算子がかかる、というのはどこかで聞いたことがある方も多いのではないでしょうか。もうちょっとだけ式をいじくってみます。
\hat{S} = (\ket{0}\bra{0} \otimes I + \ket{1}\bra{1} \otimes \hat{S}_1 \hat{S}_0^\dagger ) (I \otimes \hat{S}_0)
左側のカッコの中をよく見てみましょう。「片方量子ビットの状態が$\ket{0}$なら残りの量子ビットにIを掛ける(何もしない)、一方で状態が$\ket{1}$なら残りの$S_1 S_0^\dagger$を作用させなさい」ということです。
そう!これはどうやら制御ユニタリゲートと同じ構造になっているではないですか!
またまた具体的でない$S_0$とか$S_1$というのが出てきました。具体的な行列の構造はいったん置いておくとして、、制御ユニタリゲートはどうやって作ったらいいでしょうか?
制御ユニタリゲートの作り方
これを読んでいらっしゃる方は、制御NOTゲート(CNOTとかCXとかとも言う)はご存知かと思います。量子コンピューターの実用においては、絶対に欠かすことのできないゲートです。IBM Qでも専用のゲートが用意されています。しかし、それ以外の(一般の)制御ユニタリゲートについては専用のゲートが用意されているわけではありません。困りました。ではどうしたら良いでしょうか?ゲートとは行列で表現できるので、使用可能なゲートの行列表現の組み合わせ(積)に分解してみるということを目指せばよいのです。
幸いにして、一般の制御ユニタリゲートは、数学的に分解する方法が証明されています。(Nielsen&Chuangにも証明が書いていますので、探してみてください)
ここで3つのゲート(行列)$A,B,C$は次の性質を満たします。
ABC=I
AXBXC=U
つまり、3つを所定の順番で書けると単位行列$I$になって、間に$X$を挟むと$U$になるという$A,B,C$を探せばよいことになります。
そんな都合の良い$A,B,C$なんてあるのでしょうか?
実はあるんです!
A=U_1(\beta)R_y(\frac{\gamma}{2}) = U_3(\beta,\frac{\gamma}{2},0)
B=R_y(-\frac{\gamma}{2})U_1(\frac{\delta+\beta}{2}) = U_3(0,-\frac{\gamma}{2},\frac{\delta+\beta}{2})
C=U_1(\frac{\delta-\beta}{2})
こうなる、$\beta,\gamma,\delta$を求めればOKという話に帰着できます。すごいですね!
疑り深い方はちゃんと検算してみると勉強になります。
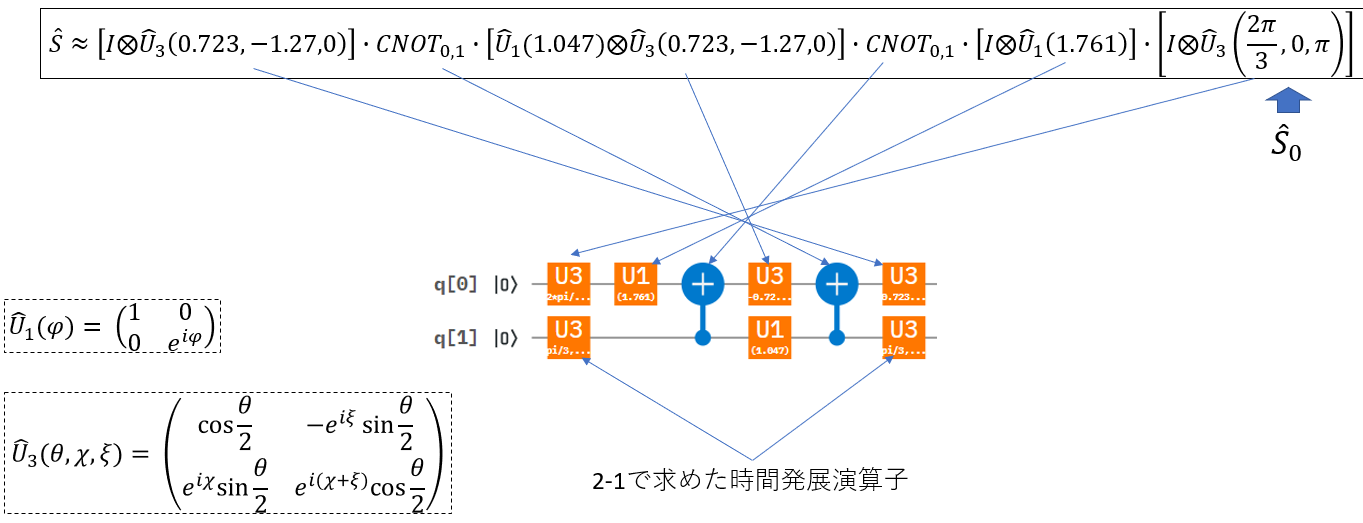
散乱演算子をゲートで表現する
さて、これで準備ができましたので、散乱演算子に具体的な行列を入れてみて、ゲートで表現してみましょう。散乱演算子の2つは以下のようにしています。(論文まま)
\hat{S}_0 =
\begin{pmatrix}
\frac{1}{2} & \frac{\sqrt{3}}{2} \\
\frac{\sqrt{3}}{2} & \frac{1}{2}
\end{pmatrix}
\hat{S}_1 =
\begin{pmatrix}
\frac{\sqrt{3}}{2} & \frac{1}{2}e^{i\pi/3} \\
\frac{1}{2}e^{i\pi/3} & \frac{\sqrt{3}}{2}e^{i2\pi/3}
\end{pmatrix}
実はここからの求め方はわからなかったので、諦めて論文の構造を利用させてもらいました。
以下のように書き出すことができるようになります。よく見ると、上で書いた$A,B,C$の構造に出てくるU1、U3がその順番に登場していることが見て取れます。
数式の順番とゲートの書く向きが逆になることに注意してください。(実装時にはここで混乱してなかなか大変でしたw)
2-3 .さらに時間発展させる
2-1での内容と同じことをします。
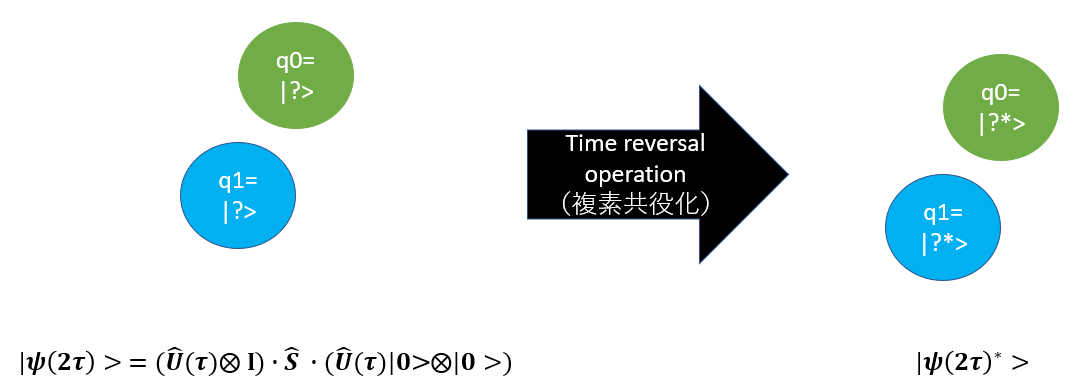
3.時間反転処理を施す
いよいよこの論文の根幹をなす部分となっている時間反転処理の実装に移ります。
時間反転処理というとすごいことのような感じがしますが、数学的にはやっていることは非常に単純で、量子状態の複素共役を取るということをするだけです。ん?そんだけ?そんだけですw
3-1.量子状態の複素共役を取る
しつこいようですが、量子コンピューターで実装するには、そういったゲートを用意する必要があるのですが、任意の状態の複素共役を取るようなゲートはあるのでしょうか?残念ながら、そういったゲート自体は用意されていません。また、任意の状態の複素共役を取る演算子はアンチユニタリ行列というユニタリとは逆の性質を持つ演算子なので、量子計算の世界には存在していません。
困りました。では、どうやって実装すれば良いのでしょうか。
そこで考えたのは、任意の状態は諦めて、複素共役を取りたい直前の状態の重ね合わせになっている各状態の位相を求めてそれを無理矢理でも良いから共役化してしまえば良いという発想です。
言葉だとわかりにくいので、例を挙げます。
まずは、以下のような2量子ビットの状態を考えます。それぞれに位相が付いていますね。今は、規格化係数などは忘れてください。
\ket{\psi} = e^{i\phi_{00}}\ket{00} + e^{i\phi_{01}}\ket{01} + e^{i\phi_{10}}\ket{10} + e^{i\phi_{11}}\ket{11}
自分の実力不足で論文の証明がきちんと理解はできていないので、説明はできませんが、結果としては、以下のようなゲートの構造を作り出せれば$\ket{\psi}$全体を複素共役化できます。
「は?嘘だろ?」って思う方は、実際に計算してみることをおススメします。任意の位相で複素共役化できます。本当によく思いついたと思います。。。研究者スゲー!
ただし、この式を見てお分かりかと思いますが、ゲートに落とし込むには、複素共役を取りたい直前の状態の重ね合わせになっている各状態の位相がわかっている必要があります。
なので、それを求める必要があります。
自分のコードでは、Qiskitのシミュレーターを使って、その状態になっているはずという状態をエラーの無い状態を仮定して、位相を求めるようにしています。
なので、任意の状態を演算子を複素共役化するゲートは作れませんが、そうできるな関数は作ることに成功しました!とは言っても大したことはありません。実部と虚部入れて分けて関数に入れてくれたら、そこから位相(Rad)を出すだけです。誰でもできる計算をさせているだけです。
def CalculationPhase(real_part,imaginary_part):
length = np.sqrt(real_part**2 + imaginary_part**2)
#real_norm = real_part / length
imaginary_norm = imaginary_part / length
if real_part >= 0 :
Rad = np.arcsin(imaginary_norm)
elif real_part < 0 and imaginary_part >=0 :
Rad = np.pi - np.arcsin(imaginary_norm)
elif real_part < 0 and imaginary_part < 0 :
Rad = -np.pi - np.arcsin(imaginary_norm)
return Rad
4.さらに時間を進める
ここでは、2と全く同じ操作(時間発展→散乱→時間発展)をして、時間を先に進めて状態を変化させます。
すると、不思議なことに、初期状態と同じ状態になります。
一応ですが、これは数学的にも証明が原論文の中でされているので、気になる方は読んでみてください。計算はそんなに難しくはない・・・はずです。
実装してみた
論文を読んでいると、2016年のIBM Q Experienceを使って実験した旨が記載されています。ということなので、論文の流れに沿ってまずは確認のために同じステップを踏みました。それを受けて、理論的な面や途中の計算をフォローできたので、それをQiskitで組み立て直し、汎用的なコードに仕立てました。
順を追って説明していきます。
まずはQ Experimenceで実装してみた
実装においては、簡単のため2量子ビットに限定しています。
細かいパラメーターは置いておくとして、まずは回路としては以下のようになります。

$\alpha=\pi/2$のケースで実装したパターンになります。一番計算が楽なので、これを最初に作りました。
Qiskitでの実装は、その過程で位相を求めるときに使ったコードを汎用化しています。
Qiskitで実装してみた
ソースコードはこちらです。自由に遊んでみてください。関数化しているので、上から動かすだけで使えます。
https://github.com/Ayumu-walker/Quantum-Computer/blob/master/TimeReversalExperiment/TimeReversal.ipynb
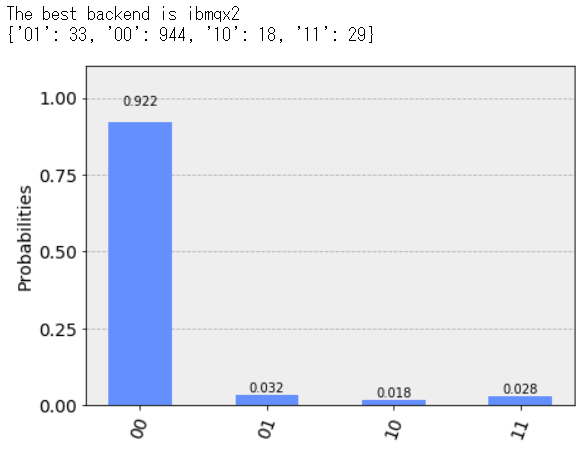
$\ket{00}$を初期状態として実機を使ってやってみた実験結果としては良好でした。ほぼ当時の論文と同じくらいの復元率が出せています。
気になること
登壇した勉強会を通じて出た質問を自分なりに解釈してみました。
00以外の状態を初期値にしても動くの?
動くはずです。たぶん。
理論的にも、初期状態には依存しませんし、コードも汎用化されているはずです。
散乱演算子Sがユニタリじゃなかったらどうなるの?
おそらく元に戻せない可能性があります。ただ、非ユニタリな散乱演算子ってどうやって実装するんでしょうね?ユニタリ演算子の積はユニタリ演算子にしかならないはずなので、実装できないかもと考えています。方法があれば、教えてください。自分でも調べてはみます。
これ何の役に立つの?
わかりませんw
これから考えていきましょう。
論文の実装個人的には楽しかったので、やって良かったw
お疲れさまでした!
今回で、最新論文の内容を実装することに味をしめたので、来年もいくつか実装してみたいと思います。すでに読み始めているのはいくつかあるのですが、自分の圧倒的実力不足と時間不足で実装が追い付かないですが、頑張ります!
余談:時間を戻しちゃったので・・・
明日の湊さんの記事に辿り着かないかも・・・?w