量子トンネル効果をQiskitでシミュレーションしてみた

これは量子コンピューター Advent Calender 2019の記事です。
@kyamazさん昨日はお疲れ様でした！

目次

1.概要
2.自己紹介
3.動機
4.量子トンネル効果とは
5.実装した論文の解説 -理論編-
6.実装した論文の解説 -実装編-
7.結果
8.終わりに

1. 概要

Pythonの量子計算フレームワークのQiskitで、量子トンネル効果のシミュレーションを行いました。

2. 自己紹介

初めまして。daveと申します。慶應義塾大学環境情報学部2年で、今年度の未踏ターゲット事業では量子機械学習プロジェクトの代表をやっております。生粋のQuantum Nativeです。

ちなみに、さっきネットワーク運用がご専門の研究室の先輩(アメリカ人)に
*"You are a quantum yakuza who is working on some weird things"って言われたので、Jay Gambettaになりきって"You are thinking too classically"*と言い返してやりました。はい論破。

3. 動機

量子コンピュータの歴史は、1982年にRichard Feynmanが__量子系のシミュレーションを効率化するために__「量子力学で元に動作するコンピュータ」の製造を提案したことから始まりました。¹
しかし、ShorのアルゴリズムやGroverのアルゴリズムなどの誕生によって、計算の高速化や省メモリ化の可能性に関心が移っていきました。事実、このAdvent Calenderの参加者の皆さんの中にもSSVQEや量子金融計算、量子インターネット等最先端のトピックを扱う方がいらっしゃいます。
その中で、あえて自分は原点に立ち返って量子系のシミュレーションについて言及したい、中でも特に元々関心があった量子トンネル効果について記事を書きたいと思い、このテーマにしました。本日は、解説と実装コードを使って一緒に量子トンネル効果の勉強していきましょう。

4. 量子トンネル効果の概要

下の図をご覧下さい。(画像は²から引用)

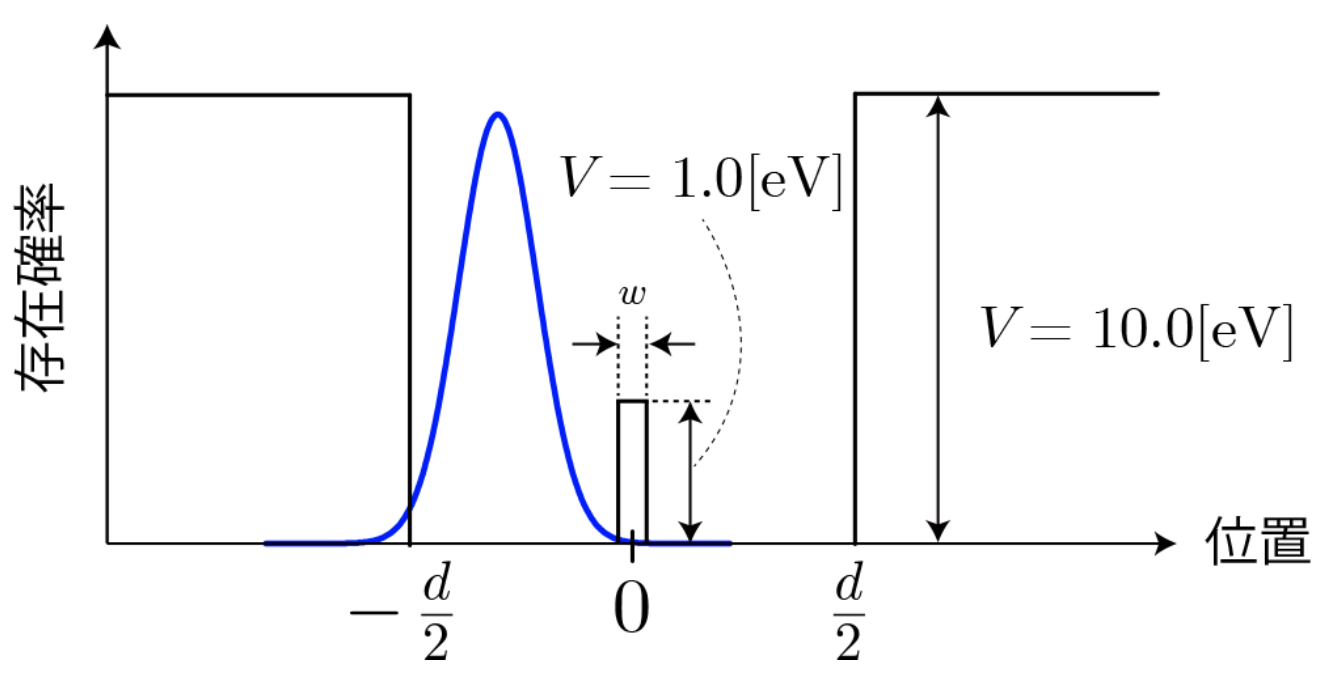
波動関数(青の曲線)が２つの10.0eVのポテンシャル障壁に挟まれているのが見えると思います。(右端の1.0eVは無視して下さい)
本来、古典系であれば自分のエネルギーより高いポテンシャルエネルギーの壁を越える(もしくははみ出る)ことは不可能ですが、この波動関数の左端がポテンシャルエネルギーの壁からすり抜けていることが分かると思います。

量子トンネル効果とは、このように、電子が自身のエネルギーより高いポテンシャルエネルギー障壁に囲まれていると仮定した時、波動関数が障壁の外の領域に確率的に存在するという現象です。
詳しい解説はこちらのリンクをご覧下さい。

5. 実装した論文の解説 -理論編-

今回はSornborger et al.(2012) を実装しました。³
今回のポテンシャルエネルギーは10(単位なし)、種類は井戸型ポテンシャル(上の図のように高い障壁が波動関数を挟み込んでいる形)を想定します。

量子のハミルトニアン$H$は運動エネルギー$K$とポテンシャルエネルギー$V$の和
$$H = K + V$$で表されます。

また、行列力学において、初期状態を$|\psi(0)\rangle$、時刻$t$の状態$|\psi(t)\rangle$とすると、$$|\psi(t)\rangle = e^{-iHt}|\psi(0)\rangle$$より、２つの状態は
$$|\psi(t)\rangle = e^{-iHt}|\psi(0)\rangle = e^{-i(V+K)t}|\psi(0)\rangle = e^{-iVt}e^{-iKt}|\psi(0)\rangle$$
と表すことができます。

ここでSornborger et al.(2012)³によると$e^{-iKt} = QFTe^{-iTt}QFT^{\dagger}$と表せるので、
量子状態$|\psi(t)\rangle$は、
$$|\psi(t)\rangle = e^{-iHt}|\psi(0)\rangle = e^{-iVt}QFT^{\dagger}e^{-iTt}QFT$$と書き換えられることが分かると思います。
ちなみに、$QFT$はQuantum Fourier Transform(量子フーリエ変換)、
$QFT^{\dagger}$はInverse Quantum Fourier Transform(逆量子フーリエ変換)の略です。

6. 実装した論文の解説 -実装編-

今回実装した量子回路は以下の画像のものです。(Sornborger et al.(2012)²より引用)

今回は2量子ビットを用いてシミュレーションを行います。
1-3個目の量子ゲートが$QFT$、4-6個目のゲートが$e^{-iT t}$、7-9個目のゲートが$QFT^{\dagger}$、最後のゲートがポテンシャルエネルギーのゲートです。
今回はポテンシャル井戸型ポテンシャルを仮定し、
各量子ゲートについて解説します。

$H_0, H_1$: Hadamardゲート
$\Omega_{01}$:$,Rx(\frac{\pi}{2})$ゲート
$Z_0$:$,,,\exp({-i \gamma c_0 \sigma^0_z \Delta t})$
$Z_1$:$,,,\exp({-i \gamma c_1 \sigma^0_z \Delta t})$
$\Phi_{01}$: $\exp({-i \gamma c_2 \text{diag}(1,1,1,-1) \Delta t})$
$P_0$: $,,,\exp({-i v \sigma^0_z \Delta t})$ = $Rz(2v\Delta t),,$($Rz(\theta) = \exp({-i\theta \sigma_z}/2)$より)
ここで、論文より、
$\gamma = -(2\pi/8)^2/\sqrt{2}$、$c_0 =-1.42$、$c_1 =-5.66$、$c_2 =22.63$、$v=10$、$\Delta t = 0.1$です。

ここで、自分が書いたプログラムをご紹介します。

from qiskit import * 
from qiskit.quantum_info.operators import Operator 
from qiskit.tools.visualization import plot_histogram
from scipy.linalg import expm
import numpy as np

# 時間発展の時間幅
delta_t = 1/10   

#係数
c0 = -1.42     
c1 = -5.66     
c2 = 22.63      
gamma = -(2*np.pi/8)**2/np.sqrt(8) 

# Zゲートの行列
Pauli_Z = np.array([[1,0],[0,-1]])
 
# Phiゲートの計算に用いる行列
mat = np.array([[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,-1]]) 

# ポテンシャルの値
v = 10 

# 定義が必要なゲートの行列
Z0 = expm(-1J*gamma*c0*Pauli_Z*delta_t) 
Z1 = expm(-1J*gamma*c1*Pauli_Z*delta_t)
Phi = expm(-1J*gamma*c2*mat*delta_t)

# OperatorモジュールでQiskitの量子回路に掛けられるようにする
Z0 = Operator(Z0)
Z1 = Operator(Z1)
Phi = Operator(Phi)

#1回あたりの時間発展
def time_evolution(circ):
    # QFT
    circ.h(0)
    circ.cu1(np.pi/2,0,1)
    circ.h(1)

    # e^{-iT \Delta t}
    circ.unitary(Z0, [0], label='Z0')
    circ.unitary(Z1, [1], label='Z1')
    circ.unitary(Phi, [0, 1], label='Phi')
    
    # Inverse QFT
    circ.h(1)
    circ.cu1(-np.pi/2,0,1)
    circ.h(0)
    circ.rz(2*v*delta_t,0) #P0 gate


def calc_probs(steps):
  qc = QuantumCircuit(2,2)
  qc.x(1)

  # stepの値が0より大きい時time_evolution関数を掛ける
  if steps > 0:
    for i in range(steps):
      time_evolution(qc)
  qc.measure([0,1],[0,1])

  backend_sim = Aer.get_backend('qasm_simulator')
  job_sim = execute(qc, backend_sim, shots=1024)
  result_sim = job_sim.result()
  counts = result_sim.get_counts(qc)
  return counts

7. 結果

結果を見る前に、実験の条件について説明します。
ポテンシャルエネルギーは10(単位なし)、時間幅$\Delta t$は$\Delta t = 0.1$、初期状態は$|10\rangle$状態です。また、ポテンシャル障壁はグラフの$|01\rangle$状態より左と$|11\rangle$より右にあると想像して下さい。
本来は波動関数の動きを見るべきなのですが、今回は可視化して分かりやすくするために、(確率振幅の2乗である)測定確率の変化を見ていきましょう。

では結果を見ていきましょう。
まずは0ステップ目の状態です。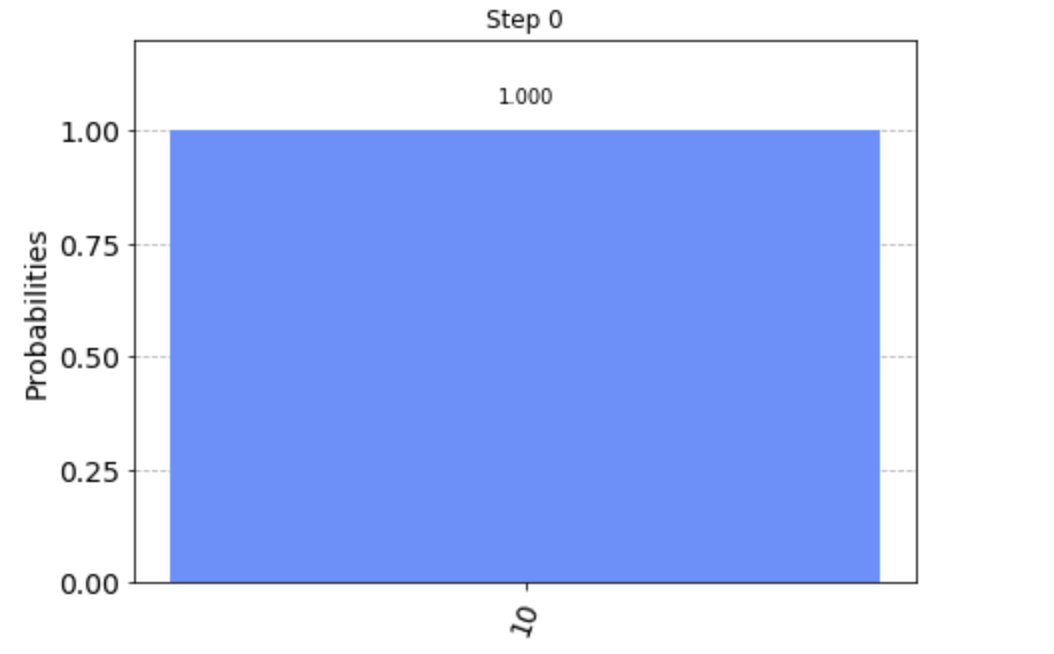まだ何もゲートは掛けていないので、当然初期状態$|10\rangle$が100%の確率で測定されます。

次に、1ステップ目です。
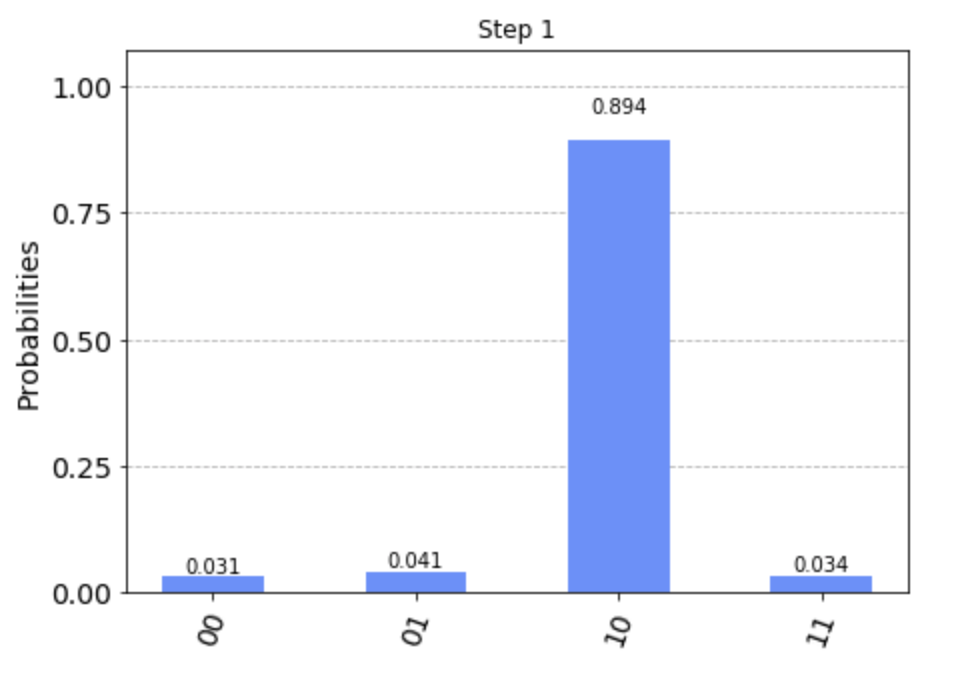わずかに他の状態の測定確率が現れました。

2ステップ目はどうでしょうか？
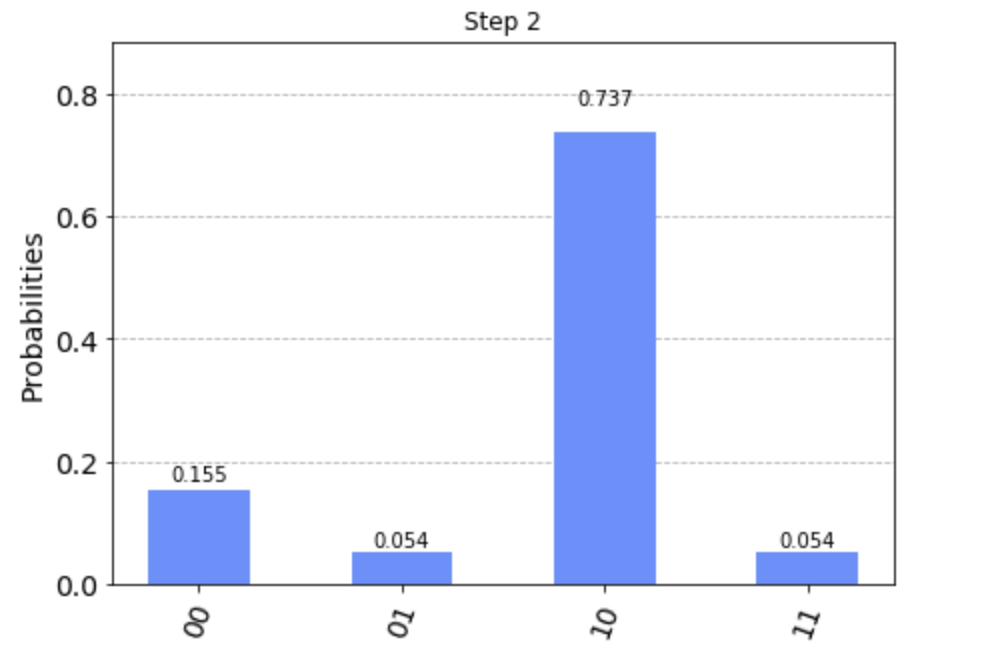$|00\rangle$の状態が増加したのが分かります。

最後に3ステップ目です。

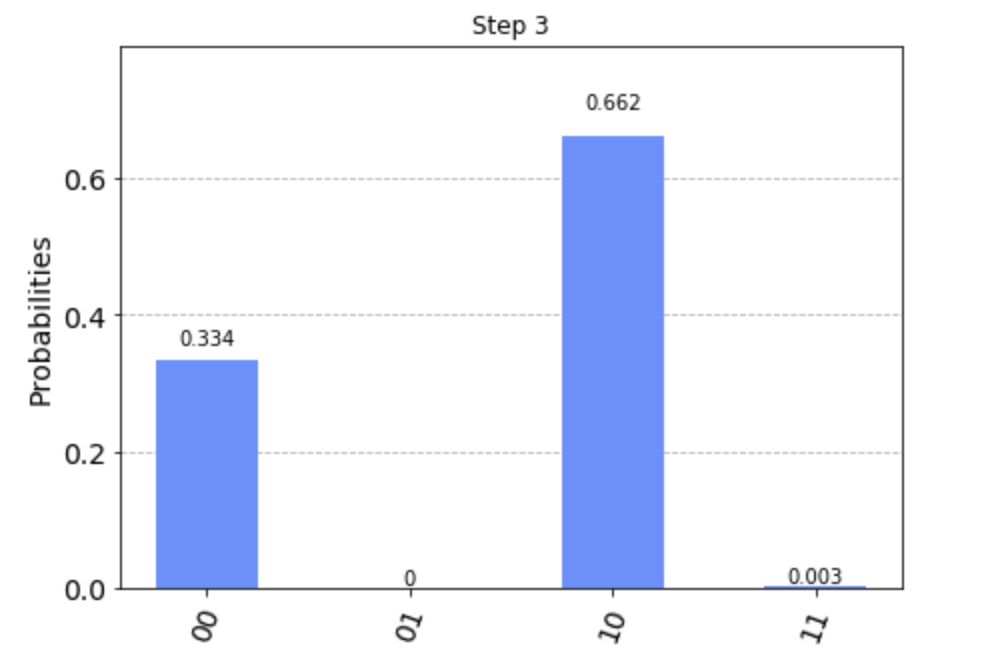
波動関数の1部($|00\rangle$状態)がポテンシャルエネルギーの壁をすり抜けたのが見て分かります。これで、量子トンネル効果がシミュレーションできたと言っていいでしょう。

8.終わりに

今回は既存の論文を元にシミュレーションを行って実際に量子トンネル効果が現れることを実証しました。今回量子コンピュータに興味があって記事を書いてみた方、NISQアルゴリズムに関心のある方、たまにはこのように小規模でも誤りのない環境下でLong-Termアルゴリズムを実装してみるのも如何でしょうか？

さて、今回は専門外の量子系のシミュレーションなので至らない点があると存じます。
もし何か「ここが違う」、「ここが分からない」等ご意見・ご質問がございましたらコメントにて教えて下さると幸いです。TwitterのDMの方が反応が早いと思うので皆様のコメントお待ちしております。

最後に、今日は量子トンネル効果を時間を「進める」シミュレーションだったのに対し、明日は@Ayumu_walkerさんの「IBM QとQiskitによる時を__巻き戻す__量子アルゴリズムの実装」です。量子コンピュータを使ってどのように時間発展を巻き戻すのでしょうか？　
@Ayumu_walkerさん、よろしくお願いします！

1. Feynman, Richard P. "Simulating physics with computers." International journal of theoretical physics 21.6 (1982): 467-488.https://catonmat.net/ftp/simulating-physics-with-computers-richard-feynman.pdf (閲覧日時2019年12月18日) ↩

2. 量子力学再入門 18】量子2重井戸中の波束の運動(スペクトル法)http://www.natural-science.or.jp/article/20180605163717.php (閲覧日時2019年12月18日) ↩ ↩²

3. Sornborger Andrew T. "Quantum simulation of tunneling in small systems." Scientific reports 2 (2012): 597. https://www.nature.com/articles/srep00597#citeas (閲覧日時2019年12月18日) ↩ ↩²