はじめに
実務でベイズ推論をやる必要があるので、事前知識として「ベイズ推論による機械学習入門」を読んで実装しています。
https://www.amazon.co.jp/dp/4061538322/ref=cm_sw_r_tw_dp_U_x_mxt0CbTB5QCRP
この本の5.3隠れマルコフモデルの実装を、自分の備忘録を兼ねて書いています。
隠れマルコフモデルの概要などは前回の記事または本を見てください。
前回、サンプルを生成してするプログラムを書きました。
https://qiita.com/AsaEagle/items/b69f7983ff5c5c1438b2
今回はその続きで、生成したサンプルをパラメータなどは知らないものとして、隠れマルコフモデルで推論してみます。
サンプルを生成
前回作成したプログラムで、サンプルを生成しました。生成しなおしてしまったので前回の記事に掲載した出力結果と違いますが、こちらのサンプルを使います。
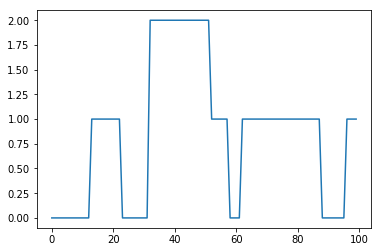
潜在変数s:[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1]
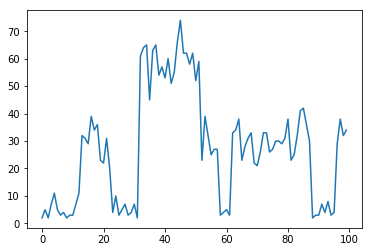
サンプルx:[2, 5, 2, 7, 11, 5, 3, 4, 2, 3, 3, 7, 11, 32, 31, 29, 39, 34, 36, 23, 22, 31, 20, 4, 10, 3, 5, 7, 3, 4, 7, 2, 61, 64, 65, 45, 63, 65, 54, 57, 53, 60, 51, 55, 66, 74, 62, 62, 58, 62, 52, 59, 23, 39, 32, 25, 27, 27, 3, 4, 5, 3, 33, 34, 38, 23, 28, 31, 33, 22, 21, 26, 33, 33, 26, 27, 30, 30, 29, 31, 38, 23, 25, 32, 41, 42, 36, 30, 2, 3, 3, 7, 4, 8, 3, 4, 29, 38, 32, 34]
隠れマルコフモデルによる推論
次に、このサンプルをもとのパラメータは知らないものとして、隠れマルコフモデルで推論してみたいと思います。サンプル$\boldsymbol{X}$が与えられた時に、そこから潜在変数の$\boldsymbol{S}$(と、その他のパラメータ)を推論します。
サンプルが、初期カテゴリがカテゴリ3つのカテゴリ分布、カテゴリ分布のパラメータπがパラメータαのディリクレ分布に従い、サンプル $x$ はカテゴリごとのパラメータ $\lambda_k$のポアソン分布に従い、その$\lambda_k$はパラメータ$a_k, b_k$のガンマ分布に従うとすると、同時分布は以下のようになります。
\begin{align}
p(\boldsymbol{X}, \boldsymbol{S}, \boldsymbol{\lambda}, \boldsymbol{\pi}, \boldsymbol{A})
&=p(\boldsymbol{X}|\boldsymbol{S},\boldsymbol{\lambda})p(\boldsymbol{S}|\boldsymbol{\pi},\boldsymbol{A})p(\boldsymbol{\lambda})p(\boldsymbol{\pi})p(\boldsymbol{A}) \\
&=p(\boldsymbol{\lambda})p(\boldsymbol{\pi})p(\boldsymbol{A})p(x_1|\boldsymbol{s_1},\boldsymbol{\lambda})p(\boldsymbol{s_1}|\boldsymbol{\pi})\prod_{n=2}^{N}p(x_n|\boldsymbol{s_n},\boldsymbol{\lambda})p(\boldsymbol{s_n}|\boldsymbol{s_{n-1}},\boldsymbol{A})
\end{align}
前回サンプルデータ生成するときは、$\boldsymbol{A}$は決め打ちにしてしまいましたが、$\boldsymbol{A}$も事前分布(K次元のディリクレ分布)で生成されるものとします。
完全分解変分推論のパラメータ更新式
本の182ページにある完全分解変分推論をやってみます。
混合分布の変分推論と同様、パラメータと潜在変数に分解して近似しますが、時系列があるので、さらに時間方向もバラバラに分解して推論します。
p(\boldsymbol{S}, \boldsymbol{\lambda}, \boldsymbol{A}, \boldsymbol{\pi}|\boldsymbol{X}) \approx \{\prod_{n=1}^{N}q(\boldsymbol{s_n})q(\boldsymbol{\lambda}, \boldsymbol{A}, \boldsymbol{\pi})\}
これを変分推論の公式
\begin{align}
\ln{q(z_i)}&=\langle\ln{p(\boldsymbol{D},z_1,z_2,...z_M)\rangle}_{q(\boldsymbol{z}_{\backslash i})}+const.
\end{align}
に当てはめて変形していき、パラメータの更新式を導出します。式の導出は本にお任せするとして、導出される式は以下のようになります。
\begin{align}
\langle s_{n,i}\rangle&=\eta_{n,i} \\
\langle s_{n-1,i},s_{n,j}\rangle&=\langle s_{n-1,i}\rangle\langle s_{n,j}\rangle \\
\langle \lambda_i\rangle&=\frac{\hat{a}_i}{\hat{b}_i} \\
\langle \ln{\lambda_i}\rangle&=\psi(\hat{a}_i)-\ln{\hat{b}_i} \\
\langle \ln{\pi_i}\rangle&=\psi(\hat{\alpha}_i)-\psi(\sum_{i'=1}^{K}{\hat{\alpha}_{i'}}) \\
\langle \ln{A_{j,i}}\rangle&=\psi(\hat{\beta}_{j,i})-\psi(\sum_{j'=1}^{K}\hat{\beta}_{j',i})
\end{align}
ただし、$\eta$はnの値に応じて、
n=1のとき
$$
\eta_{1,i}\propto exp{ \langle \ln{p(x_1|\lambda_i)}\rangle_{q(\lambda_i)}
- \langle \ln{\pi_i} \rangle
- \sum_{j=1}^{K} \langle s_{2,j} \rangle \langle \ln{A_{j,i}} \rangle } \
$$
n=2~N-1のとき
$$
\eta_{n,i}\propto exp{ \langle \ln{p(x_n|\lambda_i)}\rangle_{q(\lambda_i)} - \sum_{j=1}^{K} \langle s_{n-1,j} \rangle \langle \ln{A_{i,j}} \rangle
- \sum_{j=1}^{K} \langle s_{n+1,j} \rangle \langle \ln{A_{j,i}} \rangle } \
$$
n=Nのとき
$$
\eta_{n,i}\propto exp{ \langle \ln{p(x_N|\lambda_i)}\rangle_{q(\lambda_i)} - \sum_{j=1}^{K} \langle s_{N-1,j} \rangle \langle \ln{A_{i,j}} \rangle } \
$$
また、nがどの値でも
$$
\sum_{i=1}^{K}\eta_{n,i}=1
$$
また、
\begin{align}
\hat{a}_k &=\sum_{n=1}^{N}\langle s_{n,k} \rangle x_n + a \\
\hat{b}_k &=\sum_{n=1}^{N}\langle s_{n,k} \rangle + b \\
\hat{\alpha}_i &=\langle s_{1,i} \rangle + \alpha_i \\
\hat{\beta}_{j,i} &=\sum_{n=2}^{N} \langle s_{n-1,i},s_{n,j} \rangle + \beta_{j,i} \\
\end{align}
また、$\psi()$はディガンマ関数です。
実装
式はこんな感じなので、あとはパラメータを順に計算してループを回して推論します。
以下のようなコードを書きました。
(ループと分岐が深くてすみません。。。)
# 定数
K=3 #カテゴリ数
N=100 #サンプルデータ数
# 事前分布のパラメータ
a=200
b=5
alpha = [10,20,30] #初期カテゴリ用のディリクレ分布パラメータ
beta = [[10,10,10],[20,20,20],[30,30,30]] #状態遷移確率用のディリクレ分布パラメータ
# 更新していくパラメータ
# 初期値は事前分布と同じに
a_h = [200,200,200]
b_h = [5,5,5]
alpha_h = [10,20,30]
beta_h = [[10,10,10],[20,20,20],[30,30,30]]
# 潜在変数の期待値の初期値も設定
s_mean=[]
for n in range(N):
s_mean.append([0.4,0.3,0.3])
for i in range(10):
print("イテレーション:", i)
#パラメータからλ、π、Aの期待値を計算
lam_mean=[0]*K
ln_lam_mean=[0]*K
ln_pi_mean=[0]*K
ln_A_mean=(np.zeros((K,K))).tolist()
for k in range(K):
lam_mean[k] = a_h[k]/b_h[k]
ln_lam_mean[k]=digamma(a_h[k])-math.log(b_h[k])
ln_pi_mean[k]=digamma(alpha_h[k])-digamma(np.sum(alpha_h))
for k2 in range(K):
ln_A_mean[k2][k] = digamma(beta_h[k2][k]) - digamma(np.sum((np.array(beta_h).T)[k]))
print("lambda_mean:", lam_mean)
print("π:",math.exp(ln_pi_mean[0]), math.exp(ln_pi_mean[1]), math.exp(ln_pi_mean[2]))
print("A:",math.exp(ln_A_mean[0][0]), math.exp(ln_A_mean[0][1]), math.exp(ln_A_mean[0][2]))
print("A:",math.exp(ln_A_mean[1][0]), math.exp(ln_A_mean[1][1]), math.exp(ln_A_mean[1][2]))
print("A:",math.exp(ln_A_mean[2][0]), math.exp(ln_A_mean[2][1]), math.exp(ln_A_mean[2][2]))
#η→Sを計算
for n in range(N):
eta_tmp=[0]*K
for k in range(K):
tmp = 0
lnp_xn_lami=x[n]*ln_lam_mean[k]-lam_mean[k]
for k2 in range(K):
if n==0:
tmp+=s_mean[n+1][k2]*ln_A_mean[k2][k]
if n==N-1:
tmp+=s_mean[n-1][k2]*ln_A_mean[k][k2]
else:
tmp+=s_mean[n-1][k2]*ln_A_mean[k][k2]+s_mean[n+1][k2]*ln_A_mean[k2][k]
if n==0: eta_tmp[k]=np.exp(lnp_xn_lami+ln_pi_mean[k]+tmp)
else: eta_tmp[k]=np.exp(lnp_xn_lami+tmp)
for k in range(K):
s_mean[n][k] = eta_tmp[k]/np.sum(eta_tmp)
#a_h, b_hを更新
for k in range(K):
tmp1=0
tmp2=0
for n in range(N):
tmp1+=(s_mean[n][k]*x[n])
tmp2+=s_mean[n][k]
a_h[k] = tmp1+a
b_h[k] = tmp2+b
#α_hを更新
for k in range(K):
alpha_h[k] = s_mean[0][k]+alpha[k]
#β_hを更新
for k1 in range(K):
for k2 in range(K):
tmp = 0
for n in range(1,N): tmp+=(s_mean[n-1][k1]*s_mean[n][k2])
beta_h[k2][k1] = tmp+beta[k2][k1]
イテレーション10回回していますが、徐々にパラメータが更新されて、λ、π、Aは以下のようになりました。
$\langle\lambda\rangle$: [55.44, 31.34, 9.24]
π: [0.16, 0.32, 0.50]
A: [[0.36,0.09,0.11],[0.26,0.59,0.24],[0.37,0.31,0.64]]
どのカテゴリーがどの番号、と指定して推論するわけではないので、元のデータのカテゴリ0が推論では2、カテゴリ1が1、カテゴリ2が0になっているようですが、おおよそうまくパラメータが更新できていそうです。
このパラメータを使って確率が一番高い潜在変数Sをとってみると、
s_predict=[]
for n in range(N): s_predict.append(np.argmax(s_mean[n]))
print(s_predict)
これで
[2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1]
のように出力されました。カテゴリの番号が、元のサンプルとずれているので、元のサンプルに番号を合わせて比較してみると、
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1]
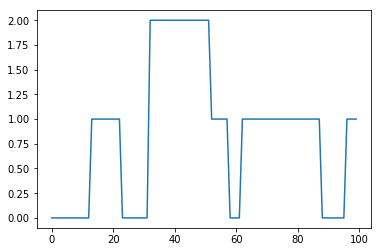
となり、元のサンプルデータの潜在変数と完全に一致しました!
サンプルによっては、微妙な値があったりすると、時々1つか2つ間違えるときがありますが、おおよそうまくできているようです。
まとめ
隠れマルコフモデルによるサンプルデータの推論ができました。
次は、このモデルを使って「将来データの予測」や「株価など実用データの推論」をやってみたいと思います。