初めに
はじめまして.社会人2年目になってしまったプログラマです.
毎度光学系の記事を書いてきましたが,懲りずに今回も光学系です.
マックス・プランク研究所の論文Physically-Based Real-Time Lens Flare Renderingを読んでなんとなく実装したので,論文内容を若干簡単にして記事にします.
今回は高速かどうかはあまり気にしてなくて,単純にカッコいいなと思って実装してみただけですのであまりパフォーマンスに気を使っていません.そもそも個人開発兼趣味の範囲なので.
実装してみた結果はこのような感じです.絞り羽根の枚数は特に固定してません.
処理時間は描画サイズ1280x720の時,ゴースト1つあたりのグリッド数16x16とした時,ゴースト数276のCanonの光学系でレイトレ・描画合わせて0.8〜1.0ms程度です.
本記事では,まず論文を簡単に解説(簡単訳)し,そのあと実際実装する際に何を考えたかなどについて記します.
よろしくお願いいたします.
論文の概要
高品質かつリアルタイムなレンズフレアシミュレーションアルゴリズムを提案しています.(イメージベースはリアリズムにかけやすく,従来の物理シミュレーションベースは計算コストが高い)
疎な(密度の低い)光束で効率よく品質の良いレンズフレアをレンダリングしたとのことです.
ジオメトリ
光学系のレンズは,平面or球面の入射面を持つレンズの集合体として扱っているので,特定のジオメトリや材料を想定してはいません.
絞り羽根
カメラ内部になる光量を調節する機構.絞り具合や羽根の枚数で形状が変化します.
光学媒体
実屈折率の完全誘電体を想定(後述されているのですが,吸収を考えていません).Sellmeierの式により,分散を記述しています.
n(\lambda) = 1 + \sum_{n = 1}^{3}\frac{B_n {\lambda}^2}{{\lambda}^2-C_n}
ここで$B_{1,2,3}, C_{1,2,3}$は製造データベースなどから得られる材質定数になります.
光の反射と透過(フレネルの式)
レイは媒体の境界で反射・透過し,反射成分はゴーストを引き起こします.これらによる光の進行方向はよく知られた反射の法則とスネルの法則に従っています.
フレネル方程式では光の偏光状態で異なる反射・屈折率となりますが,ここでは各光学系におけるP・S偏向の存在率は等しいとしています.R・Tはそれぞれ反射率・透過率です.
R = \frac{1}{2}\left(\frac{n_1 \text{cos}{\theta_1} - n_2 \text{cos}{\theta_2}}{n_1 \text{cos}{\theta_1} + n_2 \text{cos}{\theta_2}} \right)^2 + \frac{1}{2}\left(\frac{n_1 \text{cos}{\theta_2} - n_2 \text{cos}{\theta_1}}{n_1 \text{cos}{\theta_2} + n_2 \text{cos}{\theta_1}} \right)^2, T = 1 - R

反射防止膜
逆位相で振幅の等しい反射を起こす媒質を重ねると,各層での反射光が相殺して正味の反射光強度が下がります(僕のいた大学院の研究室にもこういう機能の機材があったハズ.).今回のアルゴリズムでは1/4波長コーティングを採用しています.
吸収
考えません.
回折
今回,回折により引き起こされるパターンとして,バースト(回折フレア)とゴースト(の縞・フリンジ)を考えています.実際,回折積分をセンサ全域で評価することが必要になるのですが,高コストなのでテクスチャを事前計算して使用しています.
スターバースト(回折フレア)パターン -フラウンホーファー回折-
振幅透過型の開口パターンに平行光が入射するとき,ある観測面におけるフラウンフォーファー回折波は,そのパターンの強度周波数スペクトルで与えられます.(これについては僕の記事1,僕の記事2でも解説しています.)
白色光が入射したとき,ある特定の波長について回折積分を評価し,その結果を波長方向に積分することでバーストを計算することが可能です.
つまり,特定の波長における強度周波数スペクトルを波長に関して拡縮・強度変換し,連続的に加算することで所望の結果が得られます.
ここで開口分布を$T(x,y;z = 0)$,フーリエ変換を$\mathcal{F}[\cdot]$とすれば,所望のスターバースト$I(x,y;z = z_{0})$は$F$を$T$の周波数スペクトルとして
I(x,y;z = z_0) = \int_{\lambda_{\text{min}}}^{\lambda_{\text{max}}}\left(\frac{1}{\lambda z_0}\right)^2{\mathcal{F}[T(x,y;z = 0)]}^{2}d\lambda \\= \frac{1}{{z_0}^2} \int_{\lambda_{\text{min}}}^{\lambda_{\text{max}}}\frac{1}{{\lambda}^2} {F\left(\frac{2\pi}{\lambda z_0}x, \frac{2\pi}{\lambda z_0}y\right)}^{2}d\lambda
になります.ちなみに$\frac{2\pi}{\lambda}$は波数といい$k$で表すことが多いです.

実際に皆さんが見るバーストはもう少し複雑な分布を示します.それはレンズの汚れや,傷で引き起こされる回折の影響です.これは開口画像に汚れ用の分布を与えることで実現できます.

ゴースト(リンギング)パターン
以前,僕の記事では焦点位置で周波数空間の分布に実空間の分布が変換されることを書きましたが,今回のゴーストはどちらかといえばその中間パターンとして存在します.それらは,分数次フーリエ変換(FrFT)によって計算することが可能です.
実際に論文ではOzaktas先生のFrFTを使用しているのでそちらを使用するのが良いでしょう.
僕はめんどくさかったので,かれこれよく使用している角スペクトル法(ASM)で計算しています.

角スペクトル法ではゴーストは
H(u,v;z=z) = \exp[i2\pi w(u,v)z]\\
w(u,v) = \left\{
\begin{array}{ll}
\sqrt{(1/\lambda)^2 - u^2 -v^2} & (u^2 +v^2 \leq (1/\lambda)^2) \\
0 & (\text{otherwize})
\end{array}
\right.
として
I(x,y;z = z_0) = \mathcal{F}^{-1}[\mathcal{F}[T(x,y;z = 0)]H(u,v;z=z_0)]
です.空間周波数$(u,v,w)$は実空間における信号領域の大きさを逆数とするような間隔で標本される量です.つまり,間隔$\Delta x, \Delta y$かつ点数$N_x \times N_y$で標本されている実空間の分布に対しては,$\frac{1}{N_x \Delta x}, \frac{1}{N_y \Delta y}$で標本される量です.
レンダリングシステム
ここまではレンズフレアの重要な側面をいかにモデル化するのかを記述してきましたが,ここでは実際に光の伝搬をシミュレートするレンダリング技術を解説しています.
本著では疎な光束の追跡によってシミュレーションを行っています.
センサに到達した光束は暗黙的にグリッドを構成し,その間の値は,記録された値を補間することで実現されます.
レンダリングスキーム
ゴーストの列挙
レンズ内における相互反射で発生するフレア成分であるゴーストは,偶数回の反射を伴うレイのみに起因して生じます.反射回数が2以上のものは通常無視されます.(反射防止膜などの効果で反射光強度は入射光強度に対してごくごく僅かなため)
1つの光学系に$n$個のフレネルインターフェース(レンズ)が存在するとき,ゴーストの数は$\frac{n(n-1)}{2}$個存在します.これはフレネルインターフェースの数が少し増えると爆発的な増加を示します.(例えば,今回最初のほうに結果として掲載しているNikon 28-75mmの場合,$n=$27なので352の描画対象が存在します.)
本論文では,高次の反射によるゴーストが非常に弱い強度であることからそのようなゴーストはパフォーマンス向上のためにレンダリングしないことにしています.
(一生懸命計算して画に影響しないなんてやってらんねえですからね!!)
光束追跡
今回のレンズにおける光束の追跡においては,各ゴーストにおける交差のシーケンスが正確にわかっているため,加速機構(BVHなど)は必要ありません(代数方程式によって決定される幾何構造は直線との交点を直接求められるため,特殊な構造やテクニックを必要としないということです).
レイが交差するごとに,衝突位置~光軸間の距離$r$,衝突したフレネルインターフェースの半径$r_{\text{surface}}$として$r_\text{rel}$を更新します.
{r_\text{rel}^{(\text{new})}} = \text{max}\left({r_\text{rel}^{(\text{old})}}, \frac{r}{r_{\text{surface}}}\right)
ここで,その定義から,$r_\text{rel}>1$は光学系を脱出した実際にはレンダリングされない成分になります.しかし,光束グリッドの補間に寄与するため,そのままにしておきます.(シェーダでいえばdiscardしないということです)
更に,光学系の外に出てしまったレイを,フレネルインターフェースの幾何学的側面を定義している数式を頼りに外挿することでより多くの光束が光学系の中を通過できるようにします.
これにより,光束の密度が低くても数値的な安定性が向上します.(これは,代数方程式から得られる幾何構造は,実際想定されているレンズ領域の外側まで広がっているため,光線がレンズからはみ出したとしても仮想的な局面により反射を考えることができます.この部分に関しては正直懐疑的です.アーティファクトが出る気がしなくもない.)
ラスタライズ・シェーディング
追跡された光束はセンサ面でグリッドを形成します.疎な光束ではあまり良い品質のものは得られません.著者らは隣接レイ情報を補間することで,光束全体の挙動を掴むことに関心があります.
そのため,ランダム生成された光束でなく,等間隔に配置された光束を使用します.こうすることで,センサ面におけるグリッドセルは入射面におけるそれに一致します.
ここまでで,レンズや絞りによってブロックされた光束を無視することなく,通過した絞りにおける位置(絞りのどこを通過したか),と光軸から測った距離の最大値を格納しています.これにより,対応するクアッド内で座標を補間することが可能になりました.
高速化(このあたりで熱が冷めたので取り組んでいません.)
光束バウンディング
多くの光線は遮蔽されてセンサに到達できないので,光束を開口の限られた範囲に制限します.
適応的な解像度
1光束あたりのグリッド分割数を16x16から512x512にしました.
強度LOD
最終的に得られるおおよそのゴースト強度を与えることにより,評価する最大輝度のゴースト数を調整することが可能になる.
開口カリング
開口が小さいと,光線が複数回開口を通過することはありません.(遮蔽されてしまう確率が上がりますからね.)その場合,反射する光束を無視できるので,列挙されるゴーストが減ります.
対称性
光学系が軸対称であれば,光束追跡のすべての計算が一定の方位角に制限されるため,計算量を大幅に低減できます.
GPUによる実装
基本的なアルゴリズム
頂点シェーダで光束追跡をしています.そしてジオメトリシェーダでグリッド内のクアッドからストリップを生成します.(僕はコンピュートシェーダで光束追跡し,頂点・ピクセルシェーダでクアッドを描画しています.僕はハルシェーダ・ドメインシェーダ・ジオメトリシェーダ3人衆があまり好きではありません.)
スムースシェーディング
各頂点に近傍の平均値を格納してグーローシェーディングして品質を向上しています.
論文についてはここまでにします.
実際やる際に考えたことなど
使用API
DirectX12です.
レンズの幾何構造と当たり判定
フレネルインターフェースの幾何構造は平面・球面の2種類です.
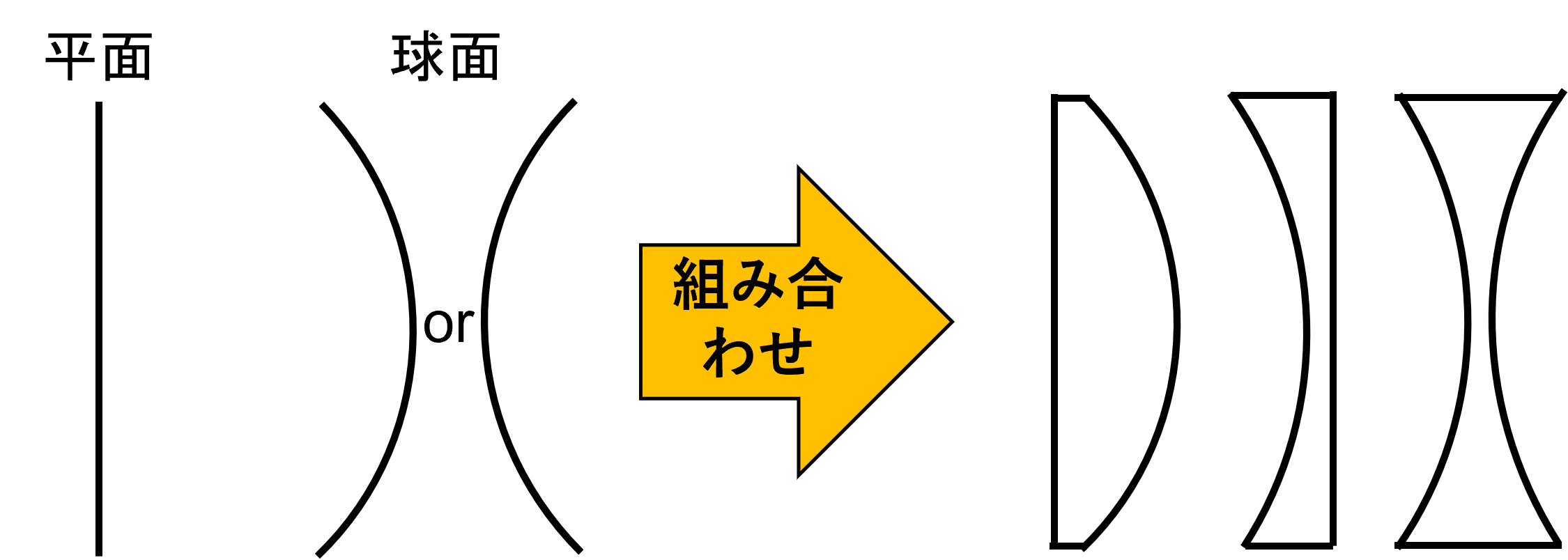
光束の追跡を行うにあたり,直線vs平面 直線vs球面の当たり判定を実装します.
特に直線vs球面の当たり判定は,ベクトル方程式を直線,球面に関して立てて,一方に代入した後,直線のベクトル方程式の位置を決めるパラメタに関する2次方程式が実数解を持つかどうかを判定すればよいです(要するに判別式が正の値をとる).
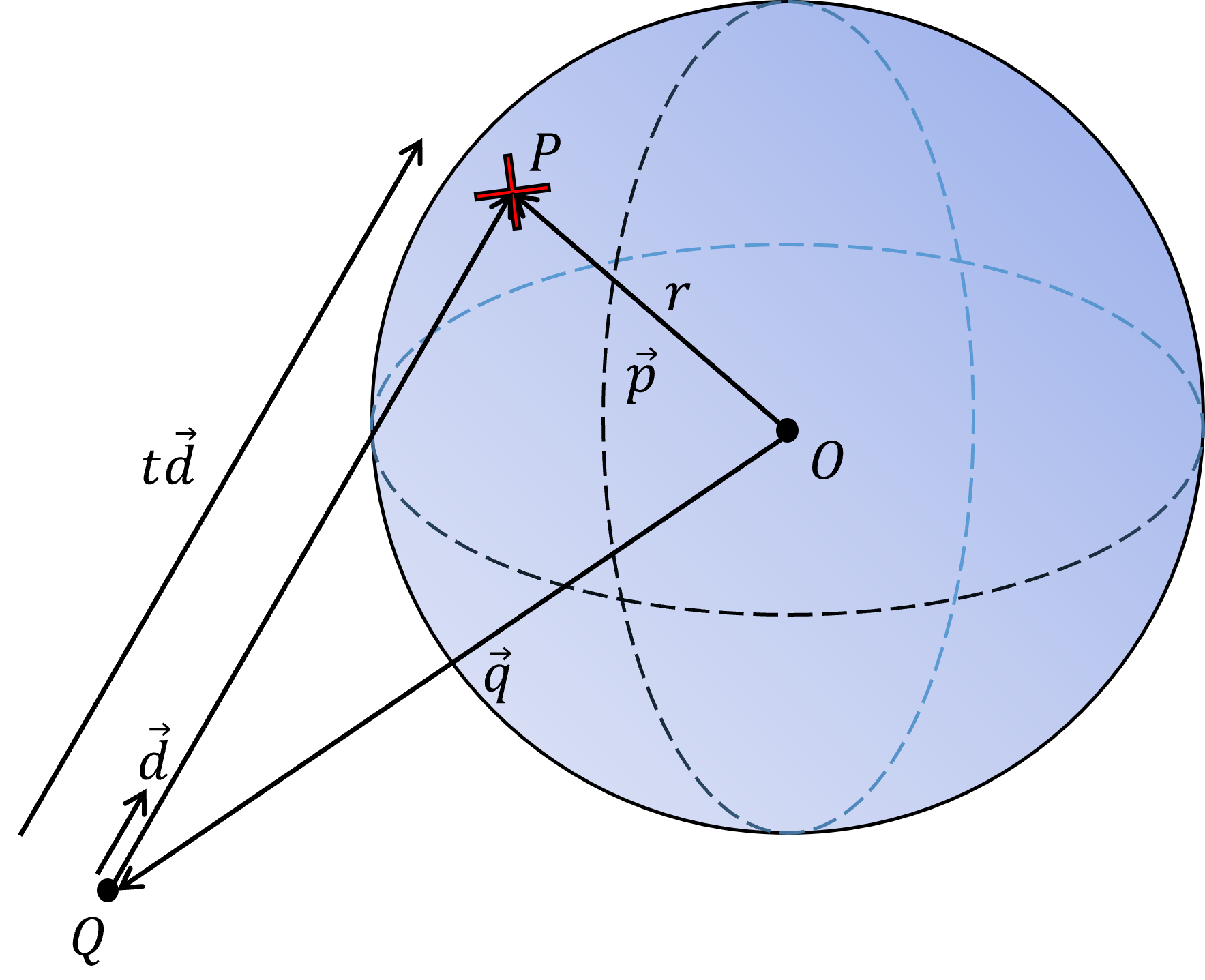
直線のベクトル方程式は
\vec{p} = \vec{q} + t\vec{d}
球面のベクトル方程式は
{|\vec{p}|}^2 = {r}^2
片方に代入して整理すると
{|\vec{d}|}^2{t}^2 + 2(\vec{q}\cdot\vec{d})t + {|\vec{q}|}^2 - {r}^2 = 0
ここで,$B = \vec{q}\cdot\vec{d}, C = {|\vec{q}|}^2 - {r}^2$として,
{|\vec{d}|}^2{t}^2 + 2Bt + C = 0
方向ベクトルは正規化されているとすると,$|\vec{d}|=1$より,
{t}^2 + 2Bt + C = 0
従って,判別式${B}^2-C<0$なら交差しない,そうでないなら交差.とすればよいです.交差したときは,$t = \sqrt{{B}^2-C}\cdot\text{sgn}(r\cdot d.z) - B$で計算します.関数$\text{sgn}(x)$は以下で定義します.
\text{sgn}(x)= \left\{
\begin{array}{ll}
1 & (x>0) \\
-1 & (x\leq 0)
\end{array}
\right.
ここで,フレネルインターフェースは負の半径を許容していることに注意してください.
ゴーストの強度計算
光束追跡した結果,センサ上における隣接する追跡結果を取得することができます.
そこで,今注目している位置における強度を近傍の衝突点と成すクアッドの面積を用いて計算します.
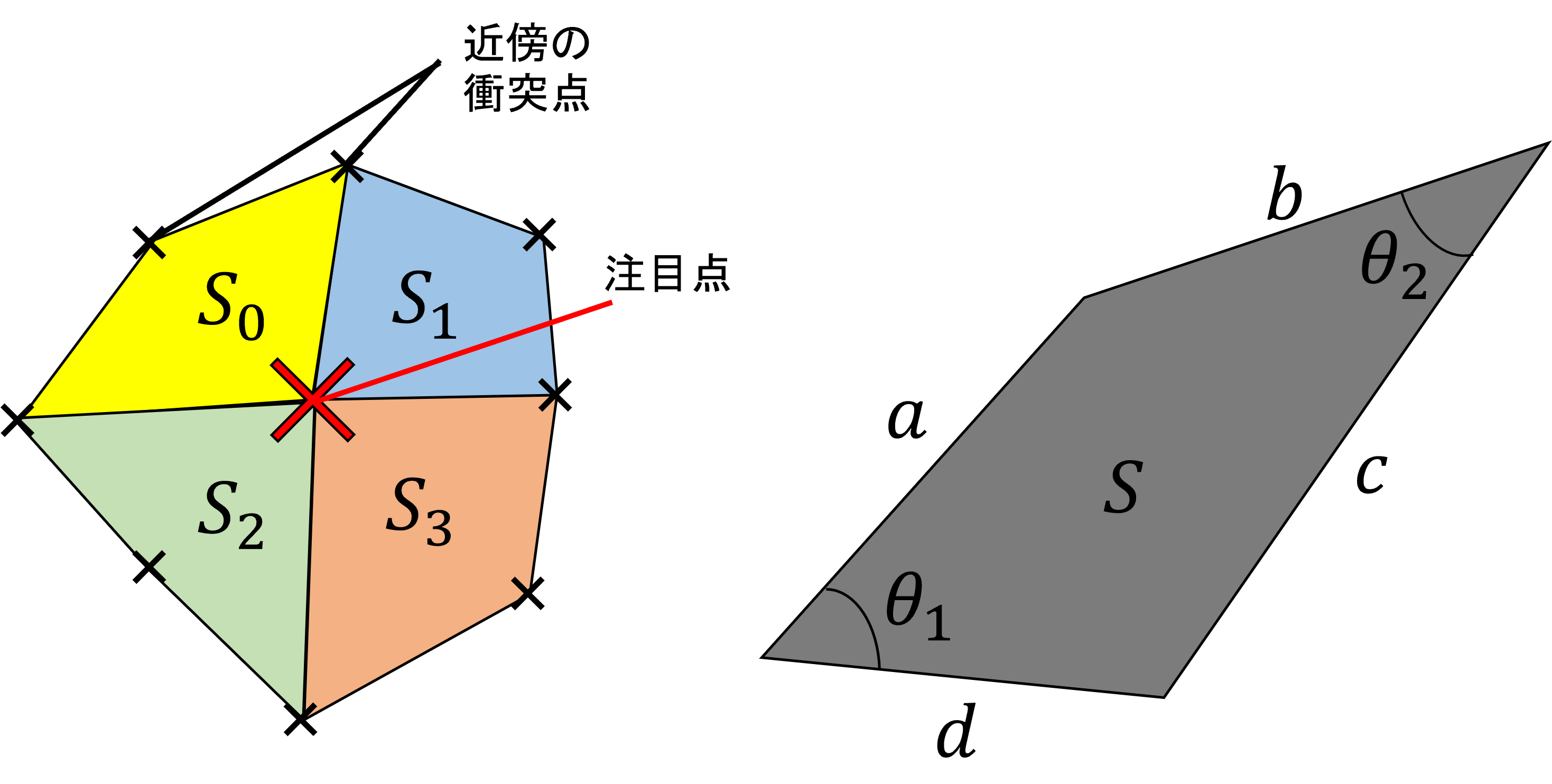

面積$S$は以下の式で評価します.
s = \frac{a + b + c + d}{2}\\
C = \text{cos}\left(\frac{\theta_1 + \theta_2}{2}\right)\\
S = \sqrt{(s-a)(s-b)(s-c)(s-d)-abcdC}
全く歪んでいないグリッドの面積$S_\text{base}$を基準として与えておいて,上式により計算した各面積の総和との比を強度として格納するのが良いでしょう($C$の右辺の余弦の角度を2で割るの忘れないで下さい.僕はうっかり忘れました.).
この場合,注目している点における強度$I$は
I = \frac{S_\text{base}}{\sum_{n=0}^{3}S_n}
で表されます.こういった計算により,コースティクスが比較的綺麗に現れます.
このような計算はkaneta1992氏の記事「webgl-waterのコースティクス解説」で取り上げられている「webgl-water」などで用いられる輝度計算です.ある面積を通過する光束が集光する(到達面における占有面積が小さくなる)ほど輝度が高くなることを表しています.

グリッド分割数について
1ゴーストを構成するグリッドの分割数は128x128あれば見た目は問題ない気がしました.グリッド分割数が少ない場合,光束の散乱具合を大きくしていると補間を用いてもあまり良い結果は得られなくなります.
以下は,1ゴーストあたりのグリッド分割数を変化させたときの見た目の変化例です.

16x16くらいがコスパ的にはいいです(ゲーム内での使用など).4x4では,破綻しているものがあります.
主な構造体
特許データを格納する構造体
struct PatentFormat {
f32 radius;//radius of sphere/plane(on xy-plane)
f32 c_thickness;//coating thicknes = lambda / 4 / n1
f32 n;//refractive indices
f32 sa_h;//nomial radius (from. opt. axis)
f32 d;//distance between lens
bool f;//is this interface a plane?
};
これを以下のような構造体に変換します.
struct LensInterface {
vec3 center;//center of sphere/plane on z-axis
f32 radius;//radius of sphere/plane(on xy-plane)
vec3 n;//refractive indices (n0 n1 n2) n0 and n2 are the refractive indices of the first and second media,and n1 the refractive index of an anti-reflective coating.
f32 sa;//nomial radius (from. opt. axis)
f32 d1;//coating thicknes = lambda / 4 / n1
f32 flat;//is this interface a plane?
FLOAT2 padding;
};
光束はグリッド分割数,インデックスバッファと頂点バッファを持つ構造体にするといいでしょう.
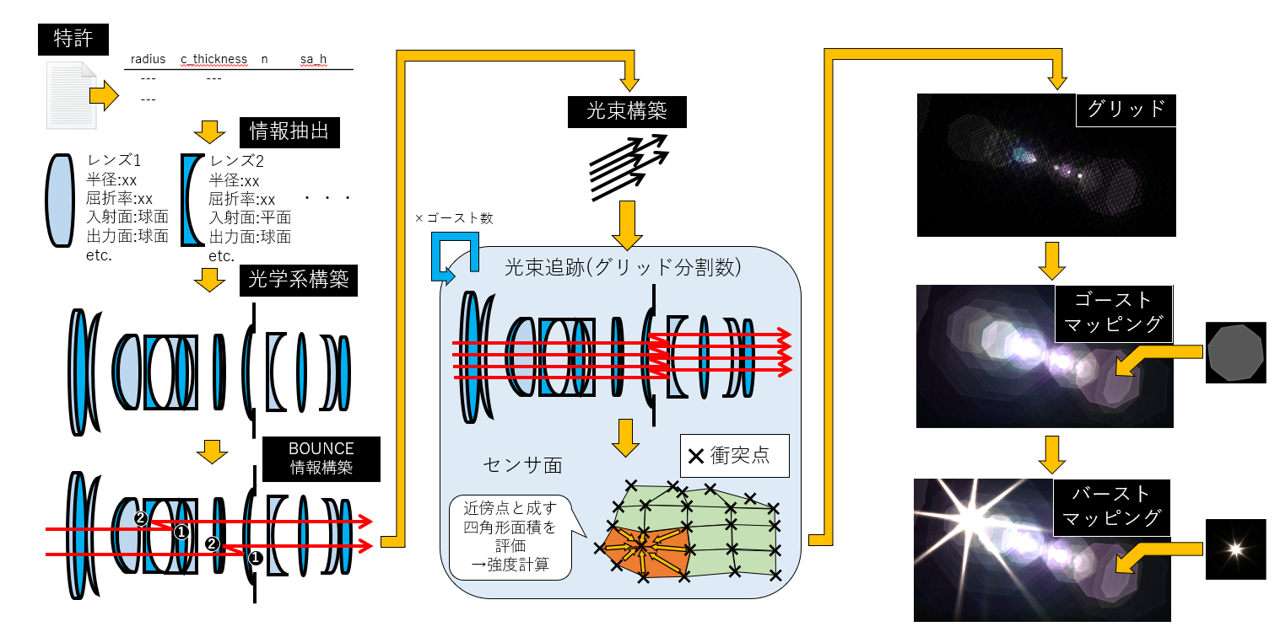
詳細なプロセス
- 特許データから光学系を形成(例えば米国の特許データ(Nikon))
- 全光線の最大反射回数を予め決定し(2回がおすすめです),それに応じて各ゴーストの形成に至った反射面の組み合わせを列挙(BOUNCE情報)
- 光束追跡+近傍衝突点との面積評価による強度計算 をゴースト数反復(コンピュートシェーダで一気に計算)→センサ衝突位置・強度・開口部通過位置・反射率を計算結果として保持
- 回折フレア・ゴースト画像を生成
- 光束追跡時の計算結果を元にグリッドにテクスチャをマッピング+強度計算し,描画
感想
なかなか時間がかかりました.しかし,非常に質の良い論文で,読んでいて飽きを感じませんでした.大学・大学院でも光学を学んでいたのですが,こういったリアルタイム技術における光学はあまり関わってこなかったので新鮮でした.
これから先もこういった論文・研究者の方々の登場により,リアルタイムレンダリング・リアルタイムグラフィックスの世界がより盛り上がり,成長していく未来を見れたら良いなと感じました.
本当に時代に恵まれたなと思います.
では今回はこのあたりにしようと思います.ここまで読んでくださった方,お付き合いいただきありがとうございました.次回は光学から離れて別分野のレンダリング技術を紹介できれば良いなと考えています.(とか言って光学持ってきそうな気はしてます.)
お疲れさまでした.ではまた.