More than 3 years have passed since last update.

ポストエフェクトクエスト - 波長方向の積分マジ大事という話 -

Last updated at 2021-02-04Posted at 2021-01-23

#初めに
前回はスターバーストについて記事を書きました．同機はポストエフェクトクエスト第一弾のバーストの見た目があまり気に食わなかったからというものでした．
実はまだ気に行っていない部分があります．なんとなく現状ではザラザラした見た目のグレアになっています．

実際，左のような画像にグレアのポストエフェクトをかけると右のようになります．

惜しい見た目なんですよね．この画像はフラウンホーファー回折で計算した回折像をRGB3波長に対してスケーリングして出力した結果でした．でもつい最近思ったんです．

###3つだけは少なすぎね!!!??

それはそうですよね．大体380[nm]～750[nm]まであるんですから．この中の3つしか使ってないってそりゃ現実離れしたグレアが出ますよね．というわけで今回はもう少しこの辺を考慮して見た目を追求していきます．

因みに最終的にこんな感じになります．

#基本のおさらい
今回も使用するものはいつものごとくフラウンホーファー回折です．レンズの集光作用について軽く復習していきましょう．
以下のように，開口$g(x,y)$から距離$R$離れた位置での回折波の光波分布を計算することを考えます．

ここで$h(x,y)$は開口面のある点$(x,y)$から焦点までの距離$r^{'}=\sqrt{f^2+x^2+y^2}$に応じて波の位相をずらす性質を持ちます．この関数は焦点距離$f$のレンズ中心を基準として

h(x,y)=\exp[-ik(r^{'}-f)]

と表されます．この時，距離$R$での分布は

u(x_0,y_0) = A^{'}\iint g(x,y)\exp[-i(ux+vy)]dxdy = A^{'}\mathcal{F}[g(x,y)]=A^{'}F(u,v)\\
A^{'}\equiv \frac{A}{i\lambda f}\exp\left[ik\left(f + \frac{{x_0}^2+{y_0}^2}{2f}\right)\right]\\
u\equiv\frac{k}{f}x_0=\frac{2\pi}{\lambda f}x_0,\; v\equiv\frac{k}{f}y_0=\frac{2\pi}{\lambda f}y_0

で表されるというものでした．出力は開口面のフーリエ変換像ですね．

ここで注目すべきは$F(u,v)$の$u,v$の式です．波長の逆数に比例しています．
つまり，ある波長$\lambda_{s}$に対してフーリエ変換像を計算しておき，そのフーリエ変換像を$\frac{\lambda}{\lambda_{s}}$倍のスケーリングをし，輝度を$\frac{\lambda_{s}}{\lambda}$倍したものがその波長のフーリエ変換像となるのです．

#波長方向に積分
以下のように，あらゆる波長に対して回折像が存在します．人間の目にはこの範囲の光がすべて飛来し，網膜に像を結びます．つまり，よりリアルなグレアを考慮するとなれば，波長方向に積分してあげる必要があります．
つまり，欲しいものは振幅として

I(\frac{2\pi}{\lambda f}x_0,\frac{2\pi}{\lambda f}y_0) = \int_{\lambda_{min}}^{\lambda_{max}}|F(\frac{2\pi}{\lambda f}x_0,\frac{2\pi}{\lambda f}y_0)|d\lambda

です．まあPCは離散化されたものしか勿論扱えませんので，この式は実際には

I(\frac{2\pi}{\lambda f}x_0,\frac{2\pi}{\lambda f}y_0) = \sum_{\lambda = \lambda_{min}}^{\lambda_{max}}|F(\frac{2\pi}{\lambda f}x_0,\frac{2\pi}{\lambda f}y_0)|

になります．はい，スケーリングしながらフーリエ変換像を加算し続けていくだけです．

#分光分布特性の考慮
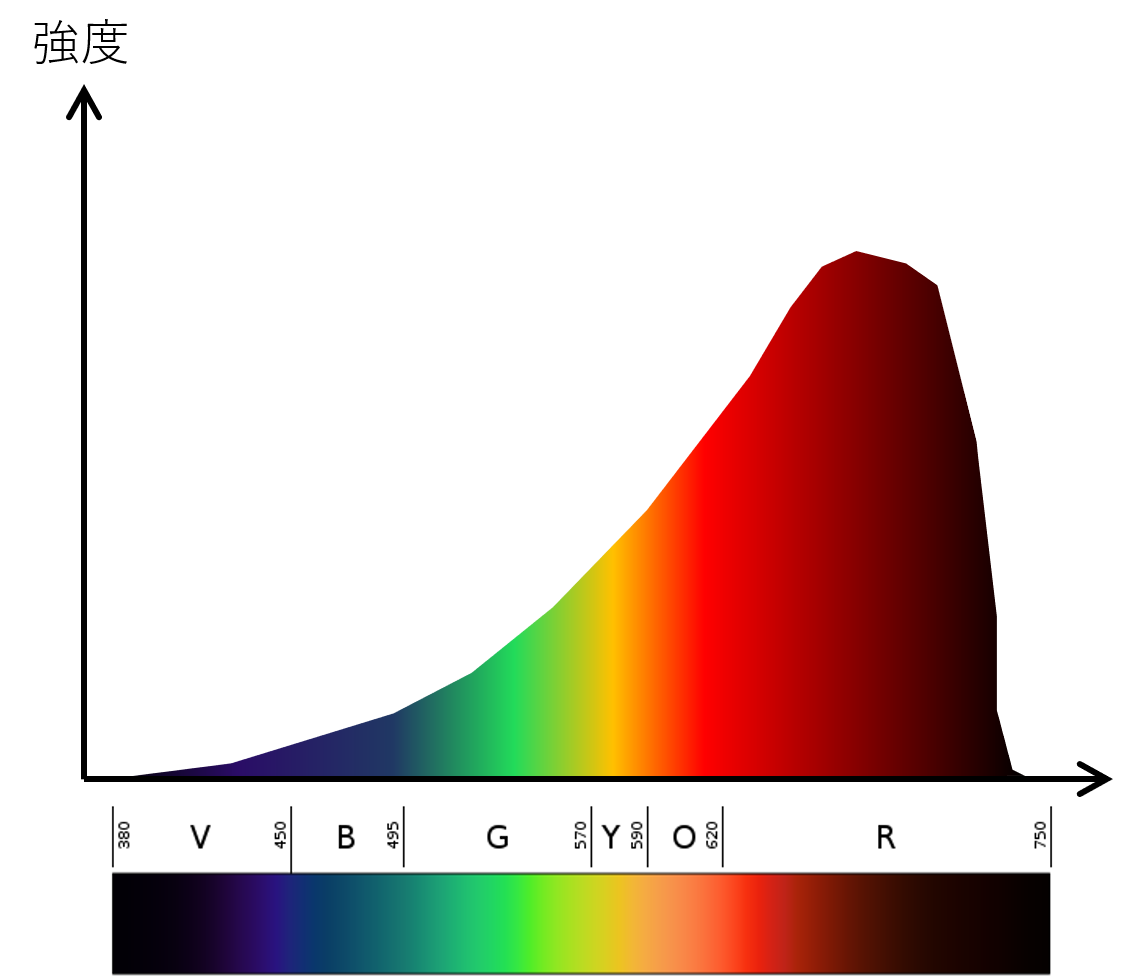
光源ごとに分光分布特性があります．どれだけその波長の成分が含有されているかを示すものです．下の図みたいなやつです．この特性曲線を$H(\lambda)$とでもしておきましょう．
すると，先ほどの式は，

I(\frac{2\pi}{\lambda f}x_0,\frac{2\pi}{\lambda f}y_0) = \sum_{\lambda = \lambda_{min}}^{\lambda_{max}}H(\lambda)|F(\frac{2\pi}{\lambda f}x_0,\frac{2\pi}{\lambda f}y_0)|

となります．
説明はこれで終わりになります．

#実装する
フーリエ変換像をスケーリングして足すにしても各サンプル波長毎に画像を用意するなんてとてもできません．そこで参照すべき画像のインデックスを各点毎に計算し，そのインデックスから得られる輝度値に分布特性を考慮した係数を乗算し加算していくというやり方をとります．

今回もポストエフェクトクエスト第一弾と被る部分が多いので変化するところだけ書きます．

HLSL


float lambdafunc(float lambdamin, float lambdamax, float lambda)
{
	return lambda / (lambdamax -lambdamin);
}

float2 indexfunc(float2 IndexStandard, float lambdamax, float lambda)
{
	float2 uvstandard = IndexStandard - float2(0.5 * WIDTH, 0.5 * HEIGHT);
	float2 uv = uvstandard * lambda / lambdamax;

	return uv + float2(0.5 * WIDTH, 0.5 * HEIGHT);
}

[numthreads(WIDTH, 1, 1)]
void mainSpectrumScaling(uint3 dispatchID : SV_DispatchThreadID)
{
	float2 indexR = dispatchID.xy;

	float maxlambda = 800;
	float minlambda = 360;

	//RGB毎に使用するサンプル数
	float samplenum = computeConstants.glarelambdasamplenum;

	float lambdarange = maxlambda - minlambda;

	float lambdaDelta = lambdarange / samplenum / 3;

	float maxr = sourceImageR[indexR].r;

	float3 result = float3(0.0, 0.0, 0.0);

	//スケーリングした先の対応画素値を参照して加算していく
	for (int i = 0; i < samplenum; i++)
	{
		float lamred = maxlambda - i * lambdaDelta;
		float lamgreen = maxlambda - (i + samplenum) * lambdaDelta;//より小さい波長からスタート
		float lamblue = maxlambda - (i + 2 * samplenum) * lambdaDelta;//同上

		float cr = lambdafunc(minlambda, maxlambda, lamred);
		float cg = lambdafunc(minlambda, maxlambda, lamgreen);
		float cb = lambdafunc(minlambda, maxlambda, lamblue);

		float2 indR = indexfunc(indexR, maxlambda, lamred);
		float2 indG = indexfunc(indexR, maxlambda, lamgreen);
		float2 indB = indexfunc(indexR, maxlambda, lamblue);

		cr *= sourceImageR[indR].r;
		cg *= sourceImageR[indG].g;
		cb *= sourceImageR[indB].b;

		result = result + float3(cr, cg, cb);
	}

	//足しただけ割る
	result /= (WIDTH*HEIGHT * samplenum);

	destinationImageR[indexR] = float4(result, 1.0);
	destinationImageI[indexR] = float4(result, 1.0);
}

ハイ終わりです．

#結果の比較
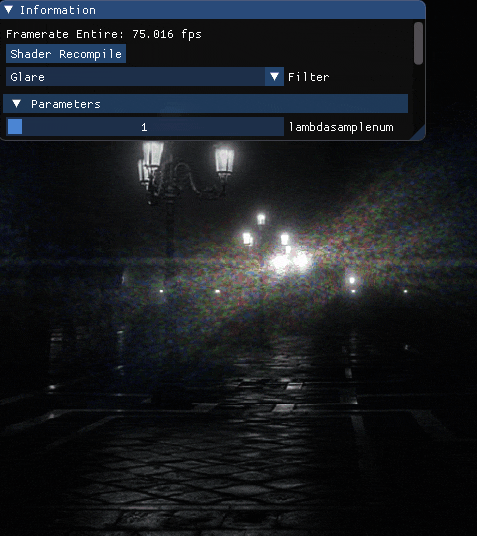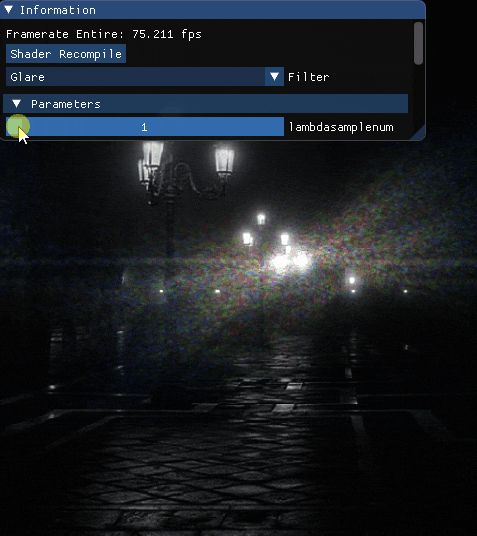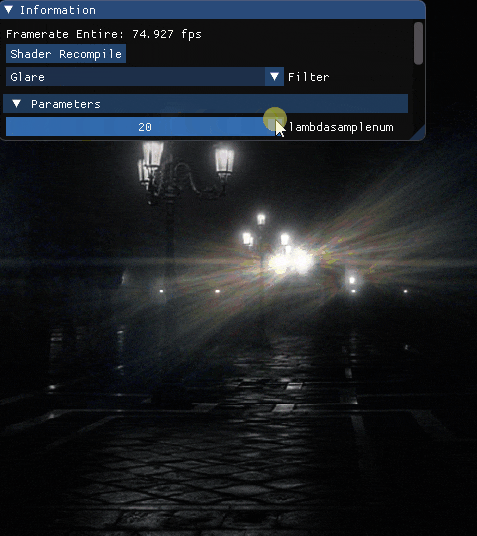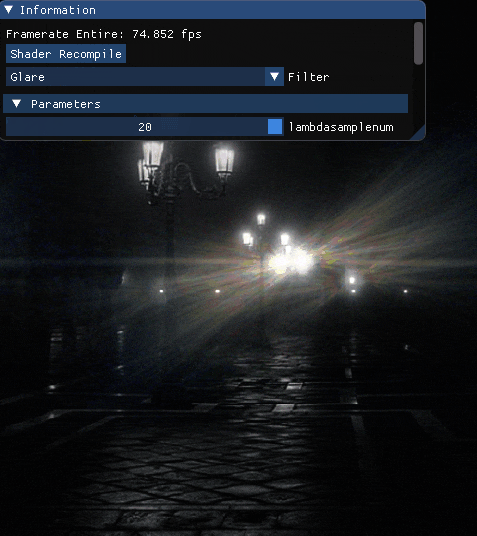
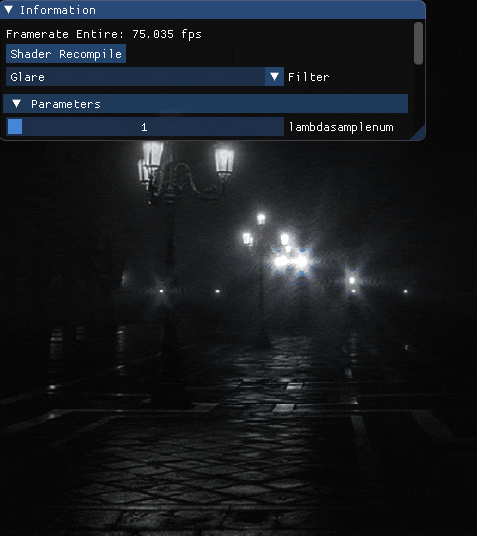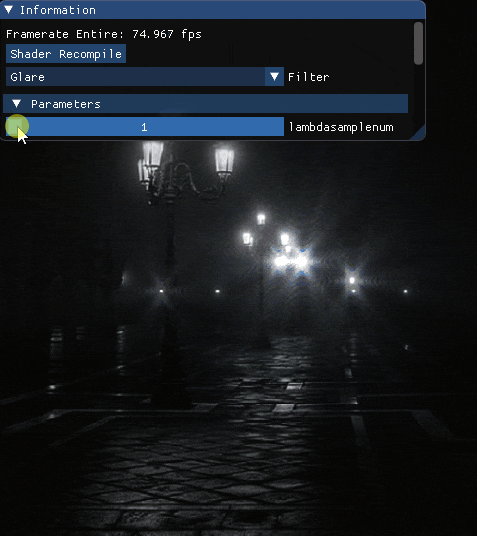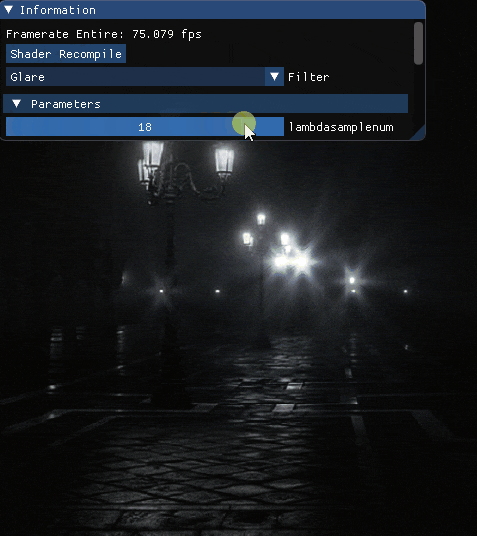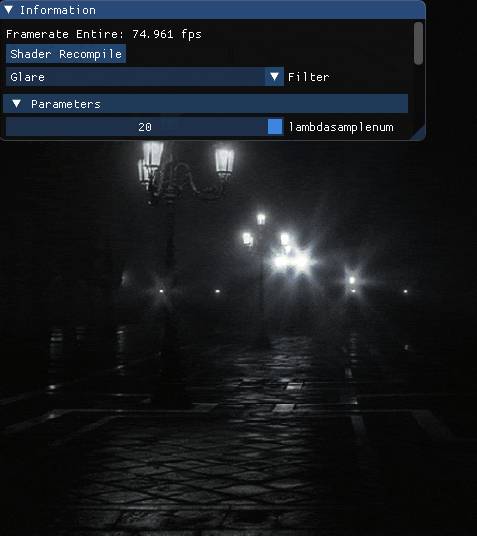
波長を最大波長を800[nm]最小波長を360[nm]としたとき，サンプル数を変化させた場合の結果を載せます．

###エフェクト単体
先ずは単体で．

まつ毛グレアの場合